SIMILAR REGULAR PLANS FOR MOBILE CLIENTS

John Tsiligaridis

Heritage University, Math and Computer Science, 3240 Fort Road, Toppenish, WA, 98948, U.S.A.

Keywords: Broadcasting, Broadcast plan, Mobile computing.

Abstract: The broadcast problem including the plan design is considered. The data are inserted and numbered into

customized size relations at a predefined order. The server ability to create a full, regular Broadcast Plan

(RBP) with single and multiple channels, after some data transformations, is examined. The Basic Regular

Algorithm (BRA) prepares an RBP and enables users to catch their items avoiding wasting energy of their

devices. In the case of multiple channels, a dynamic grouping solution is proposed, called Full Partition

Value Algorithm (FPVA) under a multiplicity constraint. The Similar Regular Plan Algorithm (SRPA)

provides faster service of the supreme sets with the use of fewer channels. The combination of FPVA and

SRPA provides flexibility for finding desired solutions. This last property, can be offered by servers today

providing channel availability and lower energy consumption. Simulation results are provided.

1 INTRODUCTION

An efficient broadcast schedule program minimizes

the client expected delay, which is the average time

spent by a client before receiving the requested

items. The expected delay is increased by the size of

the set of data to be transmitted by the server. A lot

of work has been done for the data dissemination

with flat and skewed design (Acharya et al., 1995,

Yee et al., 2002, Ardizzoni et al., 2005, Bertossi et

al., 2004). For the flat design when the cycle

becomes large the users have to wait for long until

they catch the data in case they had lost them

previously. For the skewed design ,the most

frequently requested data items should be put in fast

channels whereas the cold data can be pushed to

slow channels. Various methods have been

developed to partition the data according to their

popularity using dynamic programming (Yee et al.,

2002) , and the heuristic algorithm VFk (Peng et al.,

2000). The minimum time broadcast problem has

been addressed by computing the minimum degree

spanning tree of directed acyclic graphs in (Yao et

al., 2008). The Min-Power broadcast problem in

wireless ad hoc networks has been answered by

assigning transmission range to each node (Hashemi

et al., 2007).

When the broadcast cycle has long size, the flat

scheduling needs many channels to avoid the user

delay. The regular design with the equal spacing

property (Acharya et al., 1995) can provide

broadcasting for single and multiple channels with

average waiting time less than the one of the flat

design. It also offers channel availability, and less

energy consumption while there is no need for use of

channels with different speeds.

For the regular design, the system works with a

number of channels that could be of the same speed.

The users of all sets, except for the last one, can get

their data from the same channel. Only the users of

the last set (the most unpopular set) have to switch

to another channel. The data are considered

homogenous or heterogeneous with multiples of a

basic size. Data can be sent by a single channel or a

set of channels.

In this paper, we study the problem of finding

the number of channels that can send a group of

data, while ensuring equal spacing of repeated

instances of items. The FPVA with SRPA provides

a framework for a dynamic solution under

constraints, in the case of multiple channel

allocations. The FPVA can be extended to the case

of broadcasting updated data.

The paper is organized as follows. In Section 2,

the model description is given. The BRA is

developed in Section 3. In Sections 4,5 and 6 the

FPVA, the SRPA and their combination are

developed respectively. Finally, simulation results

are provided in Section 7.

Tsiligaridis J..

SIMILAR REGULAR PLANS FOR MOBILE CLIENTS.

DOI: 10.5220/0003602000690074

In Proceedings of the International Conference on Data Communication Networking and Optical Communication System (DCNET-2011), pages 69-74

ISBN: 978-989-8425-69-0

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

2 MODEL DESCRIPTION

2.1 The Relations in the Broadcasting

Plan

In our approach we consider three sets S

(i=1,2,3)

with their sizes S

so that S

≥ S

.The

possibility of providing full BP (it does not include

any empty slot) is examined iteratively using

relations starting from the last level of hierarchy S

The number of S

items (or items of multiplicity

(it_mu

)) will be sent at least one from S

,while for

the other two sets at least two. Given the size S

, S

from the integer divisions of S

, using

array (arr), we can create a set of relations S

div

(j< S

), with different number of relations (n_rel) and

subrelations in each set (i-subrelation, i=1,2,3). We

create a set of relations including their subrelations

by considering items of different size from each set.

Each relation has three subrelations.

The following definitions are essential:

Definition 1: The size (or horizontal dimension) of a

relation (s_rel) is the number of items that belong

to the relation and it is equal to the sum of the size of

the three subrelations (s_rel=



∑

subs

). The number

(or vertical dimension) of relations (n_rel) with

s_rel define the area of the relations (area_rel).

Example 1: The relation A=(a, b, c, d, f) has the

following three subrelations starting from the end

one; the 3-subrelation (f) with s_sub

= 1, the 2-

subrelation (b,c,d) with s_sub

= 3, and the 1-

subrelation (a) with s_sub

=1. The s_rel=5

Definition 2: The area of the i-subrelation

(area_i_sub) is defined from its size (s_sub

) and

the number of the relations (n_rel) that are selected.

It is given by (s_sub

) x (n_rel).

Example 2: From a relation with s_rel=5 and if

n_rel=5 then the area of this relation is 5x 5 .

Hence there are 25 locations that have to be

completed.

Example 3: If two relations are: (1,2,3,5,6,7),

(1,3,4,8,9,10) with s_sub

=3, s_sub

=2, then : 2-

subrelation

=(2,3) and 2-subrelation

=(3,4). The

last two subrelations ((2,3),(3,4)) comes from S

={2,3,4} having 3 as repeated item.

Definition 3: A BP is full if it provides at least 2

repetitions of items and it does not include empty

slots in the area_rel. A BP is regular if it is full and

provides equal spacing property (Acharya et al.,

1995).

Definition 4: The number of items that can be

repeated in a subrelation is called item multiplicity

(it_mu) or number of repetitions (n-rep).

Definition 5: A subrelation i (i-subrelation) that

belongs to set S

is strong if, in its area, it can

provide the same number of repetitions of all the

items of a set (without empty slots) for all the

relations. The strong i-subrelations create strong

relations.

Definition 6: Integrated relations (or integrated

grouping) is when after the grouping, each group

contains relations with all the data of S

and S

. This

happens when: (∪ (2_subrelation) = S

)

∧ ( ∪

(1_subrelation) = S

). See example 7 for details.

Grouping length(g): The g is a divisor of S

(1,..,k).

It is the n_rel that can provide homogenous

grouping. The g

stands for the various values of g.

Supreme sets (SS): are all the sets except the last

one. (SS =S

(i=1..n-1)\ S

). The last set (S

) can be

named as secondary set (SS). The divisors of SS are

named last set divisors (LD= {ld

}, for i=1..k}).

Some (or all) of the ld

values can provide an RBP

(homogenous grouping) and then ld

= g

. It is

possible all ldi values to be grouping values as well

(ld

= g

). Similar Regular Plans (SRP): are the plans

that have the same subrelations for the supreme sets

and different for the secondary set.

Example: Considering : (1) RBP

with s_sum

= 5,

s_sum

=5, s_sum

=8 and s_sum

=12,(2) RBP

with

s_sum

= 5, s_sum

=5, s_sum

=8 and s_sum

=6. The

two RBPs consist an SRP.

Partition value (pv): It is the common divisor of S

(i=1,.., k) and gl for a given size of s_sum

. Hence:

| S

and pv

| gl. Each set must have its own pv.

Example 4: If S

=40, g=20, considering that

s_sum

=8 then pv

=5 (=40/8) . Hence pv

| S

and

The criterion of homogenous grouping(chg): when

| g.

The criterion of multiplicity constraint(cmc): This

happens when: it_mu

i+1

< it_mu

(i= 1,..,n-1).

The PV criterion: when PV

> PV

i+1

The number of channels (nc): S

/ gl (where S

is the

last set)

It is considered that a|b (a divides b) only when b

mod a =0 (f.e. 14 mod 2=0). The relation with the

maximum value of n_rel provides the opportunity

of maximum multiplicity for all items of S

and S

and finally creates the minor cycle of a full BP. The

major cycle is obtained by placing the minor cycles

on line. Similar description of the relations model is

in (Tsiligaridis ,2009, Tsiligaridis et al., 2007).

DCNET 2011 - International Conference on Data Communication Networking

2.2 Some Analytical Results

Two basic Lemmas provide the possibility of the

FBP and RBP construction. The first deals with a

particular case of the S

and S

while the second is

a general case for every value of S

, S

. Proofs and

details for the case of empty slots BP are not

included in this work due to limited space.

After making sure that there is a RBP the data from

the array (the minor cycles for each array line) are

transferred to queues for broadcasting. For multiple

channels, the data from integrated relations are

grouping with GHA and then are broadcasting.

Example 5: The relation A= (a, b, c, d, f) has the

following three subrelations (s_sub

) starting from

the end one; the 3-subrelation (f) with s_sub

= 1,

the 2-subrelation (b,c,d) with s_sub

= 3, and the 1-

subrelation (a) with s_sub

=1. The size of relation

(s_rel) =5.

Lemma 1 (particular case): The basic conditions in

order from a set of data to have a regular broadcast

plan are: k= S

/ S

(1) and m= it_mu

= S

/ k (2)

(item multiplicity).

Proof: For (1) if k= S

| S

then the k offered

positions can be covered by items of S

and we can

take a full BP. From (2) m represent the number of

times (it_mu) that an item of S

will be in the

relation. •

Example 6: (full BP) Consider the case of: S

= {1},

={2,3}, S

= { 4,5,6,7,8,9, 10, 11}. Moreover k=

| S

= 4(8/2) , and m=2(4/2) the it_mu

=2=4/2 .

The relations for the full BP are: (1,2,4,5), (1,3,6,7),

(1,2,8,9)(1,3,8,9). Since (s_sub

/ s_sub

) >1 we have

r_p =4 (2*2).

Example 7: Let’s consider S

= {1}, S

={2,3,4,5},

= {6,7,8,9, 10, 11,12,13}. Again, k=2(8/4), m=

it_mu

=2(4/2). Hence the FBP is (1,2,3,6,7),

(1,4,5,8,9),(1,2,3,10,11) ,(1,4,5,12,13). The

subrelations (2,3) ≠(4,5).

Lemma 2 (general case): Given that S

and S

(and S

? S

) with k

, k

their common divisors as:

= n/S

(3) and k

= n/S

(4) (where n= common

divisors of S

and S

): (a) if k

< S

and k

(5) then there is an RBP with it_mu

= k

(b) if

> S

and S

(6) then there is an RBP with

it_mu

= S

The RBP will have for both cases k

relations.

Proof: From (3) we get that the number of S

items

in a line s_sub

= k

/ S

. From (4) we have s_sub

= k

/ S

. If (5) is valid then it means that the k

positions (offered by S

) can be covered by k

items (it_mu

). If (6) is valid then it means that the

positions (offered by S3) can be covered by S

•

Example 8: S

= {1}, S

={2,..,13}, S

= { 15,..,32}

, S

= 12, S

= 18. If n =3, k

= 3/12 =4, k

3/18=6, and k

= 6/12 = 2. Hence we have 6

relations and the 2-subrelations are:

(….,2,3,4,5,…),(…,6,7,8,9…),(…,10,11,12,13,…),

(….,2,3,4,5,…),(…,6,7,8,9…),(…,10,11,12,13,…).

If n=2, k

= 2/12 =6, k

= 2/18=9, and from k

=we have 9 ? 12.

Theorem 1: Let us consider the case of multiple

channel allocation with different multiplicity of

sets (such as: S1, S2, S3). Then, the validity of chg

can be achieved when pv

= S

/ s_sub

. If pv

| n

then g = n

and the criterion of homogenous

grouping holds.

Example 9: Let’s consider again the same four sets

S1,S2,S3,S4 with S

=10, S

=20,S

= 40, S

=120

If gl =20 (20 is a divisor of 120) then S

/ gl, S

gl, gl / S

3s.

The chg exists. The number of channels

is: nc=120/20= 6. Considering s_sum1 = 5,

s_sum

=5,s_sum

=8 then pv1 = 10/5=2, pv

20/5=4, pv

=40/8=5 and since pv

|20 ,pv

|20,pv

|20

then there is an homogenous grouping. With g =20

Theorem 2: For the lower values of LD that can

offer an RBP, we have higher values of AWT

for

supreme set and more channels.

Proof: For lower LD values the PV

has also lower

values which means greater size of all the sub

relations (s_sub

) and finally greater values for

AWTi •

2.3 The SRP

Theorem 3: For SRP increasing the LD number of

groups (gi) we have lower AWTi for supreme sets

and small number of channels.

Proof: Increasing ld

results to having less data for

the Sk (secondary set ) in the relations which

minimize the AWT

(i=1..k-1). This theorem can be

applied to FPVA. •

The number of channels is determined by the S

and

the g

(#channels= S

/ g

Example 10: Lets consider S

=10, S

=20,S

= 40,

=120 and PVA

= 2, PVA

=4, PVA

=5, PVA

=5. For g

= 10 we have: s_sub

=5, s_sub

=5,

s_sub

=8, s_sub

=12 and AWT

=15 (30/2), n_ch =

12(120/10). For g

=20, s_sub

=5, s_sub

=5,

s_sub

=8, s_sub

=6 and AWT

=14 (24/2). , n_ch =

6(120/20).

From Theorem 3 it is obvious the SRP’s ability to

provide lower values of AWT for the SRP with

fewer channels ( 12 to 6). This is the advantage the

SRP offers for the RBP design.

For any BP the upper and lower bound of AWT

(UA, LA) is depending on the size of s_sub

(i=1..n).

For a SRP, the UA and LA depend on the value of

s_sub

. They can be defined considering the

possible upper and lower values of s_sub

SIMILAR REGULAR PLANS FOR MOBILE CLIENTS

Theorem 4: For any RBP there is always a LA with

the unit correspondence.

Unit correspondence is the case when in each

relation only one item of S4 is considered. In that

case we can have the same LA for different g values

but with different n_ch.

Example 11: Let’s consider LA and for: s_sum

=5,

s_sum

=5, s_sum

=8 and s_sum

=1 with broadcast

cycle = 19 (5+5+8+1). The AWT

= 52.5 ((5*19

+10)/2).

The AWT

remains the same independently of

the value g. So if g=60 , AWT

=52.5 while n_ch =

2 (120/60). On the other hand if g=20 , AWT

=52.5

,and n_ch = 120/20 =6. The UA for the SRP can be

found for the non unit correspondence. The

max(s_sum

) can provide an UA when the

conditions to create an RBP are valid.

The conditions are: pv

| g

3 THE BASIC REGULAR

ALGORITHM (BRA)

The BRA is based on the conditions to find a RBP

and provide opportunities for multiplicity on the

items of Si (i<n) and it is for a single channel

allocation.

From all the above the model steps are: (a)

partition of data according to their popularity using

probably dynamic programming (Yee et al., 2002),

(not shown in this work), (b) construction of FBP

and RBP, (c) grouping of data lines and (d) sending

them to a minimum number of channels.

4 THE FULL PARTITION VALUE

ALGORITHM (FPVA)

The FPVA focuses on solving a problem using as

many available channels as possible and

minimizing the AWT of the supreme set

) as in Theorem 2.For all the predefined

number of integrated relations (g) we try to

discover the values of pv

(i≤n) so that the criterion

of homogenous grouping is valid and the

multiplicity constraint is satisfied.

It works with no grouping or BRA. When no

available channels exist (or when the system prefers

not to use all the available channels ) we move to the

next satisfactory solution. The LD has set the ld

an increasing order according to Theorem 2. It starts

from a maximum number of available channels

solution, tests for chg and cmc and continues until

it finds the solution with the most appropriate

number of channels. The AWT

is examined so that

when it goes above a threshold an LD increase is

made (new pace).

Example 12: Consider the sets: S

=10,S

=20,

=40, S

=120. The divisor of S

are:

LD={20,30,40}. For ld

=20 the number of channels

(if an RBP can be created) , n_ch =120/20 =6.

The divisors of S

(i≤n), D

= {8,5},

=(5,4),D

={5,2}. Taking : d

= 8,d

=5,d

=5 .

Considering as ld

=20 , s_sub

=8(=d3), s_sub

(=d2), s_sub

=5(=d1) then we have:

DCNET 2011 - International Conference on Data Communication Networking

=40/8=5, and it_mu

= 20/5=4

=20/5=4, and it_mu

= 20/4=5

pv1=10/5=2, and it_mu1= 20/2=10

So the chg and the cmc are valid (it_mu

<it_mu

) and an RBP can be created with g

= ld

If the divisors of S4 are at a decreasing order

(e.i.,60,40,20) the n_ch will take the lower value.

This is used when the design of RBP is only for a

minimum number of channels.

The RBP for all the available channels can be

achieved when the divisor of S4 are at an

increasing order. This comes from the n_cl formula

/ d

). In addition a new parameter (AWT) has be

considered and if it is above a threshold then two

choices come up: (a) apply FPVA-SRPA or (b) only

increase d

5 THE SIMILAR REGULAR

PLAN ALGORITHM (SRPA)

The SRPA focuses on providing a solution using

the available number of channels minimizing the

AWT of the supreme set (S1,S2,S3) as Theorem 3.

The new RBP can provide better AWT with less

number of channels. This is an economical solution

because with fewer channels we have faster server

service. SRPA can include all the AWT i (i≤k-1,

k=4) and not just the AWT

. A number of saving

channels (s_ch) is produced from the SRPA.

Example 13: Let us consider that: d

= 10, s_sub1=5,

s_sub2=5, s_sub3=8, s_sub4=12 and AWT

=15

(30/2), n_ch = 12(120/10). D

= {6,2} . For d

=20,

s_sub

=5, s_sub

=8, s_sub

=6 and

AWT

=14 (24/2). , n_ch = 6(120/20). We have

savings of 6 channels (12-6).

6 THE FULL PARTITION VALUE

ALGORITHM (FPVA-SRPA)

The combination of FPVA and SRPA provides the

opportunity to find a new RBP with possibilities to

change the parameters in order. First, the FPVA

finds an RBP and then the SRPA finds the most

desirable solution (lower number of channels) by

saving more available channels that could be used

for another broadcasting. It works as FPVA but it

uses an additional step, the SRPA.

7 SIMULATION

For our simulation, Poisson arrivals are considered

for the mobile users’ requests. The items are

separated into three categories according to their

popularity using Zipf distribution. Three scenarios

have been developed:

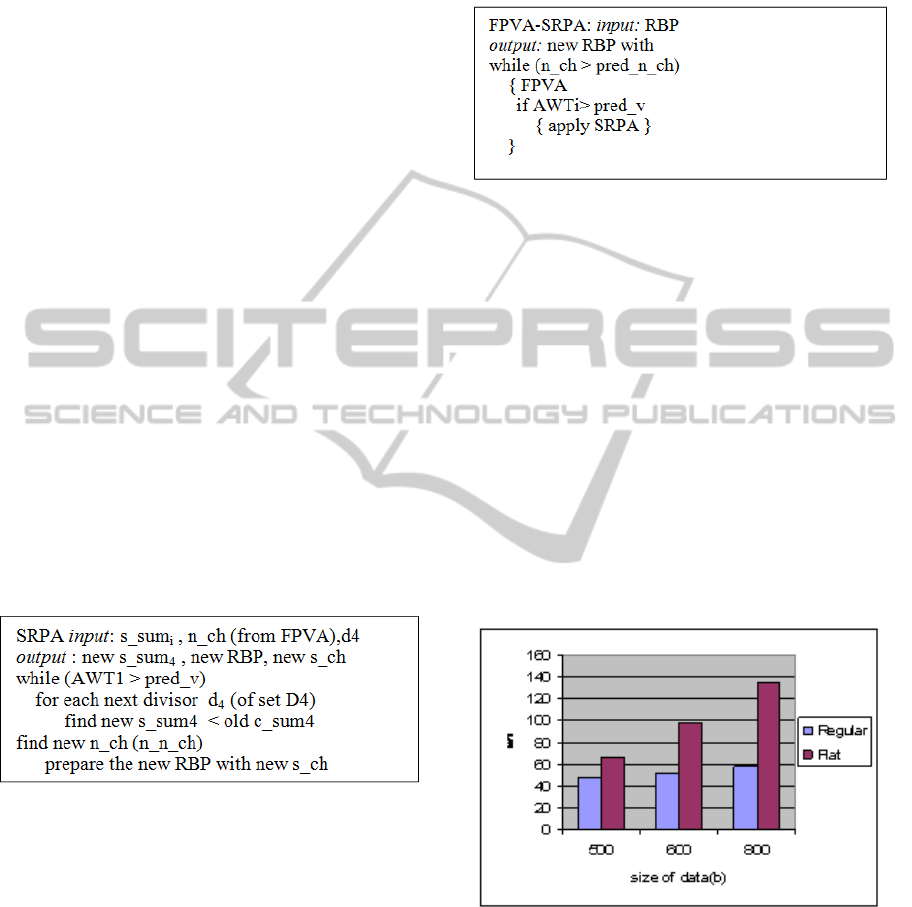
Scenario 1: In Fig. 1, data in various sizes with

equal spacing (RBP) from S

and S

sets, and flat

(for all the sets) (Acharya et al., 1995) with long

broadcast cycle size are depicted. For the data with

equal spacing the AWT is less than the one of the

flat data. It is considered a single channel service.

We will also take the same results of the RBP for the

users interested in data of S

, S

if more channels

were used.

Figure 1: The AWT for regular and flat data.

Scenario 2: Considering S

= 120,

=60,S

=40,S

= 20. The AWT for S

remain the same (Fig. 2) because PAV could find

the same values of pv

for all the number of

channels(6,3,2).The AWT

has increasing trend,

and it depends on the # of channels the PAV

discovers. The lower the # of channels is the greater

the AWT

. For S

it is considered that for each

relation there is one element (no repetitions). In

SIMILAR REGULAR PLANS FOR MOBILE CLIENTS

other words the s_sub

(i=1,..,4) remains the same

for all the cases of the number of channels.

Figure 2: The AWT for the same s_sub

Scenario 3. This is the SPRA approach. Let us

consider: S

= 120, S

=60,S

=40,S

= 10 and same

values of s_sub

from all the sets except the s_sub

In that case s_sub

diminished from 4 to 2 with

increasing g (from 30 to 60). The n_ch is reduced by

a factor of two (from 4 to 2). As shown in Fig.3

there is almost a double increase of AWT

(from

339tu to 609tu). The AWT for the other sets

) has only a small difference. This is due to

the combination of increasing g and diminishing

s_sub

Figure 3: New AWT for SPRA.

8 CONCLUSIONS

A new framework for a broadcast data model plan

with a set of algorithms is presented. Our proposed

model with parametric changes can guarantee faster

service with fewer channels for the supreme set.

Applying these algorithms the next generation

servers and their components with the scale up

possibilities, tools etc can enhance their self-

sufficiency, self-monitoring so that they may also

address quality of service, and other issues with

minimal human intervention.

REFERENCES

Acharya, S., Zdonik, F., Alonso, R., 1995. “Broadcast

disks: Data management for asymmetric

communications environments“, Proc. of the ACM

SIGMOD Int. Conf. on Management of Data, San

Jose, May 1995, 199-210

Yee, W., Navathe, S., Omiecinski, E., Jemaine, C., 2002.”

Efficient Data llocation over Multiple Channels of

Broadcast Servers”, IEEE Trans. on Computers,

vol. 51, No.10, Oct 2002.

Ardizzoni, E., Bertossi. A., Pinotti, M., Ramaprasad, S.,

Rizzi, R., Shashanka, M., 2005.” Optimal Skewed

Data Allocation on Multiple Channels with Flat per

Channel”, IEEE Trans. on Computers , Vol. 54,No. 5,

May 2005

Bertossi. A., Pinotti, M., Ramaprasad, S., Rizzi, R.,

Shashanka, M., 2004. “Optimal multi-channel data

allocation with flat broadcast per channel”,

Proceedings of IPDS’04, 2004, 18-27

Peng, W., Chen. M., 2000. ” Dynamic Generation of data

Broadcasting Programs for a Broadcast disk Array in a

Mobile Computing Environment”, Proc. of the 9

ACM International Conference on Information and

Knowledge Management (CIKM 2000), pp. 38-45

Yao, G., Zhu, D., Li, H.,Ma. S., 2008. “ A polynomial

algorithm to compute the minimum degree spanning

trees of directed acyclic graphs with applications to the

broadcast problem”, Discrete Mathematics, 308(17),

3951-3959.

Hashemi, S., Rezapour, M., Moradi, A.,2007. ”Two new

algorithms for the Min-Power Broadcast problem in

static ad hoc networks” , Applied Mathematics and

Computation, 190(2) 1657-1668, 2007

Tsiligaridis, J., 2009. “Regular Data Broadcasting Plan

with Grouping in Wireless Mobile Environment”,

International Conference on Computer Networks and

Mobile Computing, (ICCNMC 2009), WASET,

August 26-28, Singapore.

Tsiligaridis, J., Acharya, R., 2007. “An adaptive

Broadcasting Model in Mobile Information Systems”,

International Conference on Computer Information

Systems and Industrial Management Applications

(CISIM 2007), June 28-30, Elk, Poland, pp.203-209.

DCNET 2011 - International Conference on Data Communication Networking