AN APPROACH TO MODELING LANDUSE CHANGE
AND FOREST MANAGEMENT ON A GLOBAL SCALE
Mykola Gusti
ESM, International Institute for Applied Systems Analysis, Schlossplatz 1, Laxenburg, Austria
IID, Lviv National Polytechnic University, 12 Bandery Str., Lviv, Ukraine
Georg Kindermann
ESM, International Institute for Applied Systems Analysis, Schlossplatz 1, Laxenburg, Austria
Keywords: Global forest model, Landuse change modelling, Forest management modelling, Policy assessment, REDD.
Abstract: A geographically explicit approach to modelling landuse change and forestry on a global scale and a
respective model are presented. The model simulates decisions of virtual land owners on landuse change
(afforest or deforest) and forest management. The decisions are made in cells of a regular geographic grid
(e.g. 0.5x0.5 deg). Landuse change decisions are based on comparison of net present values of forestry and
agriculture. Forest management decisions are taken considering wood demand, forest productivity and net
present value of forestry comparing to a baseline. Pricing of carbon stored in forest biomass, litter and soil
alters forest net present value thus influencing landuse change and forest management decisions. Proposed
approach allows estimation of marginal abatement costs for Reduced Emissions from Deforestation and
Forest Degradation (REDD) comparable across countries or regions.
1 INTRODUCTION
Researchers often face a problem: how to make a
detailed projection comparable across many
countries? Similar approach should be applied to all
countries. In case of modelling landuse change and
forest management amount of consistent data
available in countries differs and in most cases is
limited to the data compiled by the international
organisations (e.g., Food and Agriculture
Organisation – FAO, secretariat of the United
Nations Framework Convention on Climate Change
– UNFCCC, the Ministerial Conference on the
Protection of Forests in Europe – MCPFE etc.) or
global studies like Global Land Cover 2000 (JRC,
2003), multimodel net primary production (NPP)
assessment (Cramer et al., 1999) etc. Also a limited
number of projections of factors that can be used as
drivers of landuse change and forest management on
country scale or a finer scale (e.g., GGI Scenario
Database, 2007) exist.
The problem is to find among the data a set of
drivers that can describe the landuse change and
forest management patterns plausibly.
Benítez and Obersteiner (2003) applied
comparison of net present values (NPV) of
alternative land uses as a core of landuse change
decision making on a grid-cell scale of a
geographically explicit model for Latin America. In
such approach the main landuse change drivers are
gross domestic product (GDP), population density,
forest productivity, forest share and agriculture
suitability of the land. The approach was found
successful and was further developed by
Kindermann et al. (2006), Benítez and Obersteiner
(2007) and Gusti et al. (2008). The model was
named Global Forest Model (G4M). Modeling of
forest management was introduced into the model to
take into account interdependence of afforestation,
deforestation and forest management processes
(Gusti, 2010 a, b).
Current version of G4M is designed to provide
projections of afforestation and deforestation rates,
forest management options and respective carbon
dioxide emissions and sinks, and their response to
180
Gusti M. and Kindermann G..
AN APPROACH TO MODELING LANDUSE CHANGE AND FOREST MANAGEMENT ON A GLOBAL SCALE.
DOI: 10.5220/0003607501800185
In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2011), pages
180-185
ISBN: 978-989-8425-78-2
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

climate policies in a form of carbon tax or incentive
payments. The model can help in policy assessment
for the ongoing international negotiations on
agriculture, forestry and other land use and REDD in
the frameworks of the post-Kyoto climate
agreement. G4M results have been used for a
number of assessments such as the Eliash Review,
the Economic Assessment of Post-2012 Global
Climate Policies, Roadmap for Moving to a Low-
carbon Economy in 2050, and applications
www.forestcarbonindex.org and OSIRIS. The latest
model results are discussed in (Böttcher et al, 2011).
Objective of the paper is to present the latest
developments of the modeling approach and the
model description in an integrated manner. A
number of new features were developed since the
last publications containing comprehensive model
description (Kindermann et al., 2006) and (Gusti et
al., 2008). The new features are: virtual forest, forest
management, interaction of landuse change between
grid cells, interaction of landuse change and forest
management. The model structure has been modified
as well.
2 MODEL DESCRIPTION
2.1 General Structure of the Model
Thematically the Global Forest Model is composed
of three parts – environmental (natural conditions
and forest parameters), economic (estimation of
local - cell specific - wood and agricultural land
prices, NPV of forestry and agriculture, forest
harvesting and planting costs) and decisions
(decisions on forest management parameters and
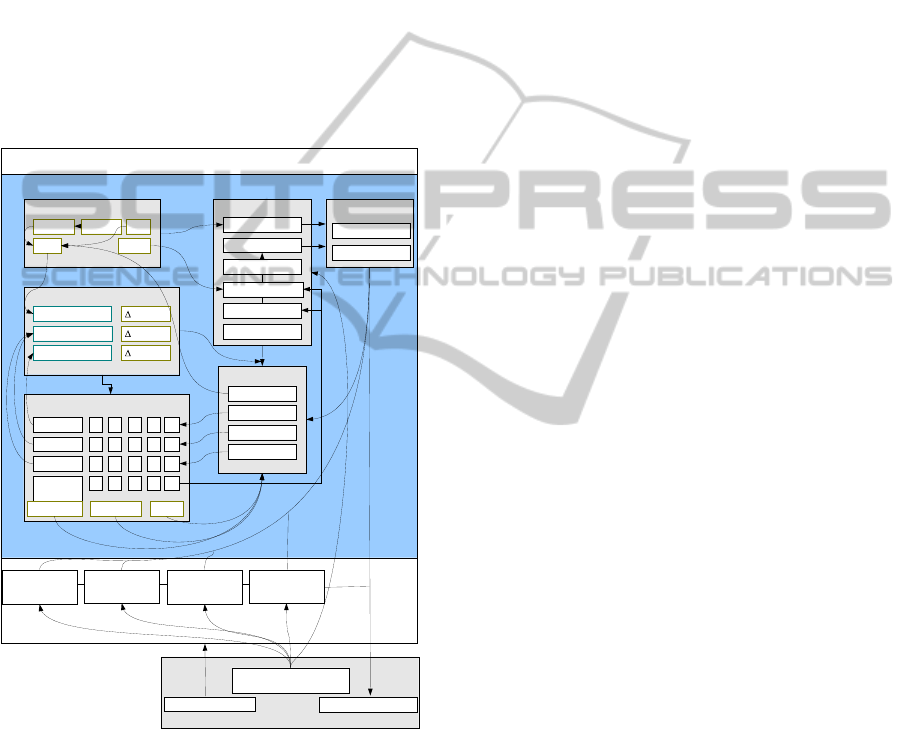
landuse change). The model flowchart is shown in
figure 1.
The model consists of five major modules:
Virtual forest, Forest initialisation, Forest
management decisions, Landuse change decisions
and Forest dynamics. The virtual forest module
simulates forest growth and management on a forest
scale. It is used in the other modules. The forest
initialisation is run only once at the very beginning.
The module creates forest in each cell and sets initial
parameters of the forests according to observed
values. The forest management decisions module is
run every year to adjust forest rotation length and
thinning to match wood demand on country or
region scale taking into account carbon sequestration
policies. The landuse change decisions module is
run every year to estimate NPV of forestry and
agriculture in order to set the cell to one of the three
states – afforest/deforest/no change, and estimate
rate of the landuse change. The forest dynamics
module applies forest management and landuse
change with the estimated parameters to the virtual
forest.
To take into account influence of trade by wood
and agriculture commodities on the local prices of
wood and agricultural land G4M is linked with the
global biomass optimisation model (GLOBIOM,
www.globiom.org).
2.2 Virtual Forest Module
The module simulates forestry on a scale of huge
forests. A generic forest growth function is in the
module core. The module allows creation of a forest
with specified environmental and forest management
parameters including growth function parameters,
highest mean annual increment of a normal forest -
MAI, yield table stocking degree - SD, rotation
length - RL, thinning, harvest losses, forest area and
age structure information. Forest is represented with
a set of forest plots of N age classes (N=RL+1; one
year step) of different area determined by the forest
age structure. Forest parameters (biomass, height
and diameter of trees) develop with age following
the growth function and scaled by MAI.
The virtual forest module provides thinning and
harvest according to the specified parameters
bringing forest to “normal” state gradually. The
module determines RL that is optimal for getting
maximal mean annual increment and maximal
sustainable harvest every year (RL
MAI
), getting
maximal biomass (RL
maxBm
), or keep current
biomass (RL
Bm
) for specific growth conditions
described by the highest mean annual increment
(MAI) and thinning intensity described by the
stocking degree related to yield tables (SD). Usually
RL
MAI
is the shortest, and RL
maxBm
is the longest
among the rotation lengths considered.
2.3 Forest Initialisation Module
In each grid cell, where forest exists according to an
initial land cover map (e.g. GLC 2000 can be used
(JRC, 2003)) or can grow, if planted according to
potential vegetation map (Rammakuty and Foley,
2009) two virtual forests are created – ‘old forest’
and ‘new forest’. Area of the old forest is set to the
observed one and area of the new forest is set to 0.
Mean annual increment is estimated from the NPP
map (Cramer et al., 1999).
Site parameters averaged over a grid cell
(climate, soil type, altitude, slope and NPP)
AN APPROACH TO MODELING LANDUSE CHANGE AND FOREST MANAGEMENT ON A GLOBAL SCALE
181

determine forest productivity and, together with
country scale economic data, land price and
harvesting costs.
The forest parameters are initialized iteratively
using geographically explicit or country specific
information. Increment is determined using a map of
potential NPP translated into MAI. MAI was scaled
at country level to match MCPFE data. Age
structure and SD are used as additional information
for adjusting MAI. If SD of forest modelled with a
given age structure (country average) in a cell is >
1.05, age structure of the modelled forest is shifted
iteratively by a few years towards older forest. If
stocking degree of forest modelled in a cell is < 0.5,
age structure of the modelled forest is shifted
iteratively by a few years towards younger forest.
Figure 1: Global Forest Model flowchart.
It is required that the shifts are symmetrical to
keep country average age structure close to
statistical value. If the age structure shift distribution
is skewed towards older forest, the country’s
average MAI is increased iteratively. If the age
structure shift distribution is skewed towards
younger forest, country’s MAI is decreased
iteratively.
In case of non-uniform age structure SD is
determined as a relation of yield table biomass of a
fully stocked stand to the observed biomass. If age
structure information is not available, normal forest
is created and SD is set to one.
Six forest management types that influence
further forest management decisions are identified
depending on site productivity, initial forest
management map (FM
map
) and profitability of
forestry comparing to agriculture (Gusti 2010a).
Rotation length of managed forests is set to
RL
MAI
, RL
Bm
or RL
maxBm
depending on whether
wood harvest within a country is smaller, equal or
greater than domestic wood demand. If RL
Bm
is
smaller than RL
MAI
we use RL
MAI
to avoid transition
effect resulting in temporal decrease of harvest even
if the rotation length is changed to RL
MAI
.
2.4 Forest Management Decisions
Module
Every simulation year all cells are processed one by
one. In the input file, which contains data for each
grid cell, the cells are sorted by countries, then
descending by MAI, amount of carbon in
aboveground biomass, forest area, population
density and agriculture suitability. Thus productive
forests of larger area and closer to populated places
are processed first. Harvested wood in a cell is a sum
of final harvest, pre-final harvest (thinning) and
wood obtained from deforestation decreased by a
country-specific slash burn factor. A sum of
harvested wood in a country is compared to
domestic demand in the country. If demand is
greater than supply by more than 2%, rotation length
of forest in cells (that belong to the country) is
decreased gradually (five-year time step) up to
RL
MAI
one by one until demand is satisfied. If after
processing all cells in the country, demand is still
greater than supply by 2%, unmanaged forest is
turned to managed, cells with population >0 or with
more productive and profitable forest are taken first.
If harvest in a country is greater than demand by
2% rotation length of less productive forests is
increased gradually (five-year time step) up to
RL
maxBm
. If after processing all cells in the country,
harvest is still greater than demand by 3%, RL of
managed forests in the country is increased
gradually up to RL
maxBm
until the 3% threshold is
reached. Forest management type is changed to
unmanaged if the supply-demand difference is more
than 5% after the previous actions.
When modeling forest management response to a
carbon sequestration incentive in a form of carbon
tax with a carbon price we consider a hierarchy of
interests: country must provide wood amount
Site
Increment
tC/ha
DBH
Height
Yield
Stocking degree
Age / Tree Size
NPP Slope
AltitudeClimate Soil
Forest
Age
Area
Biomass
Tree
Size
0 1 2 3 ...
Economic
Harvesting costs
FM Decisions
Area
Thinning
Rotation time
Sawnwood CostsPulpwood
Species
Planting costs
Wood price
LU Decisions
Afforest
Deforest
Land price
Forestry NPV
GLOBIOM
Wood demand
Wood price market corr.
Land price market corr.
Land use change
CELL 1
COUNTRY OR REGION
CELL 3CELL 2 CELL NCELL ....
Wood demand
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
182

matching the demand and create conditions for
carbon sequestration (both are on country scale) by
adjusting forest management; every year forest
owners adjust forest management to get NPV not
smaller than the NPV at zero carbon price (NPV
bau
).
Wood production satisfying wood demand at
country scale is of the highest priority. We use a two
step procedure.
STEP1. Every year, starting from 2011, forest
management in each cell is disturbed by increasing
RL. For the forest used for wood production, where
NPV estimated for the RL
maxBm
(NPV
wc
) is greater
than the NPV
bau
(NPV
bau
≥0), RL is increased
proportionally to the (NPV
wc
-NPV
bau
)/NPV
bau
. If the
NPV condition is not satisfied RL is increased
proportionally to the carbon price and saturates at
50$/tC reaching 5 year increment. In all cases
RL≤RL
maxBm
. NPV for the new RL is estimated
(NPV
c
). NPV in all cases is estimated for the time
span left to the end of the period considered.
STEP 2. Since production of wood balancing
wood demand has higher priority than the carbon
sequestration, after Step 1 the forest management of
forests within each country is adjusted to harvest as
much wood as the country wood demand. When
adjusting the forest management it is required the
new NPV multiplied by an adjustment hurdle
coefficient to be greater or equal NPV
c
estimated on
Step 1. The adjustment hurdle varies from 1 to 2500.
If the total harvest does not match wood demand, the
hurdle is increased by 0.3 and the forest
management adjustment is repeated for the forests
within the country again. Total number of iterations
is limited to 50 to avoid infinite loops. We assume
that the forest owners getting NPV smaller than
NPV
bau
are compensated by the government that is
not reflected in the algorithm explicitly.
2.5 Landuse Change Decisions Module
Land use change decisions for each grid cell are
made by comparing NPV of forestry and NPV of
agriculture. Deforestation happens in a cell if the
NPV of agriculture plus benefits from selling wood
after clear-cut is greater than the NPV of forestry
multiplied by a hurdle coefficient (a calibration
parameter that captures institutional barriers to
sustainable forest management). Afforestation
happens in a cell, in which the environmental
conditions are suitable for forestry and the NPV of
forestry is greater than the NPV of agriculture.
The NPV of forestry is a function of the MAI,
stumpage wood price and planting costs. The MAI
together with rotation length determine amount of
harvestable wood. Stumpage wood price is a
function of non-forest area and population density in
the grid cell. Planting costs are defined through
planting costs in the reference country (Brazil)
decreased by natural regeneration in the grid.
Stumpage wood price and planting costs are scaled
by purchasing power parity (PPP) relative to the
reference country.
The NPV of agriculture is modelled with an
agricultural land price in a form of Cobb–Douglas
production function, in which agricultural suitability
and population density are independent variables.
The NPV of agriculture in current grid is scaled by
PPP relative to the reference country. To take into
account deforestation pressure on forest frontier in
neighbour cells the NPV in current cell is modified
proportionally to the largest non-forest land area in
surrounding cells.
The deforestation rate (amount of forest land that
can be converted to agricultural land during one
year), and afforestation rate represent differences in
capacity to implement land use changes, e.g.
technical, infrastructural and financial capabilities of
deforesting or establishing new forests. Thus,
deforestation and afforestation rates are modelled as
a function of GDP, population density, forest area
and agricultural suitability.
2.6 Forest Dynamics Module
The forest dynamics module applies estimated forest
management parameters to the virtual forest, inserts
harvested wood and forest biomass into respective
arrays to form output data. Then the forest
management decisions are executed and consistency
check is done.
In the module emissions caused by deforestation
and carbon sink due to afforestation are estimated.
The emissions from deforestation include emissions
from burning of slash, dead wood and coarse roots,
and from decomposition of wood products, litter and
soil organic matter. The afforestation carbon sink is
due to biomass increment in growing trees,
accumulation of forest litter and soil organic matter.
To assess the emissions and carbon sink dynamics
we track evolution of all carbon pools over time
applying ecosystem-specific emission rates.
If impact of climate policy is estimated all of the
carbon pools are credited or debited. The emitted (or
sequestered) carbon multiplied by the carbon price
enters the NPV comparison for landuse change
decision making.
AN APPROACH TO MODELING LANDUSE CHANGE AND FOREST MANAGEMENT ON A GLOBAL SCALE
183

2.7 Input Data
G4M uses parameters that are defined on different
scales: global (e.g., decay rate of long and short
living products, carbon price), regional (e.g., relative
stumpage wood price and net present values of
agriculture), country (e.g., corruption factor, risk-
adjusted discount rate, forest planting costs, GDP,
hurdle, afforestation and deforestation rate
adjustment coefficients) and grid (e.g., population
density, agricultural suitability, NPP, forest biomass,
litter and coarse woody debris, potential vegetation,
protected areas, etc.). Some model parameters
change with time following B2 IPCC scenario:
population density, GDP (market), minimum
agricultural land secured to feed the population and
land under infrastructure. Main parameters of the
model and data sources are summarized in Table 1.
Table 1: Main G4M parameters.
Parameter Resolution Reference
Relative price
change for
wood and
agriculture land
Region
GLOBIOM
PPP Country
World Bank, 2005
MAI Country
MCPFE
http://forestportal.efi.int/
view.php?id=1895&c=E
1
Slash burn
factor
Country
Kindermann et al., 2006
GDP,
Population
density
0.5x0.5 deg
Grubler et al. 2007
Land under
infrastructure,
secured
cropland
0.5x0.5 deg
Tubiello and Fischer,
2007
Forest share 0.5x0.5 deg
JRC, 2003
NPP 0.5x0.5 deg
Cramer et al. 1999;
Potential
vegetation
0.5x0.5 deg
Ramankutty and Foley,
1999
Agriculture
suitability
0.5x0.5 deg
Ramankutty et al., 2002
Forest biomass,
litter and coarse
woody debris
0.5x0.5 deg
Kindermann et al., 2008b
Protected forest 0.5x0.5 deg
WDPA Consortium, 2004
2.8 Model Interlink with GLOBIOM
In G4M the prices of agricultural land and wood are
local, i.e. they are estimated for each grid-cell
independently. Thus commodity market effects are
not taken into account. But in reality interregional
trade influences the prices and consequently land-
use change and forest management decisions. To
take into account the commodity market effects we
linked G4M with a bottom-up partial equilibrium
model of total land use GLOBIOM
(www.globiom.org), which is being developed at
IIASA. G4M provides GLOBIOM with initial prices
of stumpage wood and agricultural land, which are
averaged for 27 world regions. Using the initial
prices and the carbon price GLOBIOM calculates
dynamics of the prices. In G4M the prices for each
grid cell are estimated by multiplication of the grid
cells’ prices for the base year and respective price
changes for the respective region of GLOBIOM.
GLOBIOM determines equilibrium commodity
prices for agricultural and forest sectors, matching
supply quantities with demand quantities for
regional aggregates accounting for interregional
trade. Population and GDP driving basic demand for
forest products and agricultural commodities follow
similar trajectory as in G4M.
2.9 Model Calibration and Validation
Afforestation and deforestation rates are controlled
with three country-specific calibration coefficients:
afforRate, deforRate and hurdleLUC. The
hurdleLUC coefficient controls balance of the
forestry NPV and agriculture NPV thus influencing
the landuse change decisions. The afforRate and
deforRate control afforestation and deforestation
rates in the cells where one of the processes is
active. Using the coefficients one can calibrate the
model to match country landuse change data
averaged over a certain period. Matching a trend in
the landuse change rate is also possible if data for
more than one period is available. In particular we
used FAO (FAO, 2010) or UNFCCC
(www.unfccc.int) data for the calibration depending
on requirements of a project for which the model is
run.
The model performance was tested against
independent estimates for Ukraine (Gusti et al.,
2009) as well as by comparison with similar models
(Kindermann et al., 2008b). G4M sensitivity was
studied by Gusti (2010c). Recently G4M has been
validated with national experts of individual
countries in the European Union.
4 CONCLUSIONS
Presented approach to modelling afforestation,
deforestation and forest management in one complex
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
184

model allows taking into account interactions
between the processes and making assessment of
REDD policies applying similar method in all
countries. The model is designed to use data
available at different scales (from local, grid cell
specific to global). One of the important
requirements to the data composition is consistency
of all constituents. The approach proves its validity
by providing plausible results compared against
independent estimates and tested by national experts
in EU countries. The model results are widely used
for integrated assessment purposes or in other
applications.
Further research: To improve performance of the
model in tropics we plan to introduce initialisation
of deforestation in cells using remote sensing data
and add a road network that is shown to be an
important deforestation driver (Kirby et al, 2006).
ACKNOWLEDGEMENTS
We are grateful to Michael Obersteiner and Hannes
Bottcher for useful ideas on model development and
comments on the model performance, and Andriy
Bun for helping with model code.
The model development was supported by the
following EC funded projects: CC-TAME,
ClimateCost, BEE Project, GEO-BENE, INSEA.
REFERENCES
Benitez P. C. and Obersteiner M., 2006. Site identification
for carbon sequestration in Latin America: A grid-
based economic approach. Forest Policy and
Ecconomics, 8:636–651.
Böttcher H., Verkerk H., Gusti M. et al. 2011. Projection
of the EU27 forest carbon sink and effects of recent
bioenergy policies using two advanced forestry
models. Under preparation
Cramer W, Kicklighter D. W, Bondeau A. et al, 1999.
Comparing global models of terrestrial net primary
productivity (NPP): Overview and key results. Global
Change Biology, 5(S1): 1–15.
FAO, 2010. Global Forest Resources Assessment 2010.
Main Report. Food and Agriculture Organization of
the United Nations, Rome, 2010, 375p.
GGI Scenario Database, 2007. International Institute for
Applied System Analysis (IIASA) GGI Scenario
Database, http://www.iiasa.ac.at/Research/GGI/DB/
Grubler A., Nakicenovic N., Riahi K. et al, 2007.
Integrated assessment of uncertainties in greenhouse
gas emissions and their mitigation: Introduction and
overview. Technological Forecasting and Social
Change, 74 (7): 873-886
Gusti M., Havlik P., Obersteiner M., 2008. Technical
Description of the IIASA Model Cluster. The Eliasch
Review. Office of Climate Change, UK.
Gusti M., Havlik P., Obersteiner M., 2009. How much
additional carbon can be stored in forests if economic
measures are used and how much could it cost?
Research Reports of the National University of
Bioresources and Nature Management of Ukraine,
Issue 135.
Gusti M., 2010a. An Algorithm for Simulation of Forest
Management Decisions in the Global Forest Model.
Artificial Intelligence, 4: 45-49
Gusti M., 2010b. An Algorithm for Simulation of Forest
Management Response to Carbon Price Incentive.
Proceedings of the conference ‘Modern Information
Technologies in Economy, Management and
Education”, 12 November 2010 Lviv, pp. 94-97
Gusti M., 2010c. Uncertainty of BAU emissions in
LULUCF sector: Sensitivity analysis of the Global
Forest Model. Proceedings of the 3rd International
Workshop on Uncertainty in Greenhouse Gas
Inventories, LPNU, Lviv, 299p. - pp.73-80.
JRC 2003. The Global Land Cover Map for the Year
2000. GLC2000 database. European Commission
Joint Research Centre; http://www-gvm.jrc.it/glc2000
Kindermann G., Obersteiner M., Rametsteiner E. and
McCallcum I., 2006. Predicting the Deforestation–
Trend under Different Carbon–Prices. Carbon Balance
and Management, 1:15
Kindermann G., McCallum I., Fritz S., Obersteiner M.,
2008a. A global forest growing stock, biomass and
carbon map based on FAO statistics. Silva Fennica,
42(3): 387-396
Kindermann G., Obersteiner M., Sohngen B., et al, 2008b.
Global cost estimates of reducing carbon emissions
through avoided deforestation. PNAS, 105 (30):
10302–10307.
Kirby K., W. Laurance, A. Albernaz, et al. 2006. The
future of deforestation in the Brazilian Amazon.
Futures, 38: 432-453
Ramankutty N., Foley J. A., Norman J., McSweeney K.,
2002. The global distribution of cultivable lands:
current patterns and sensitivity to possible climate
change. Global Ecology & Biogeography, 11(5): 377-
392.
Ramankutty, N., and J. A. Foley, 1999. Estimating
historical changes in global land cover: croplands from
1700 to 1992. Global Biogeochemical Cycles, 13(4):
997-1027.
Tubiello F. N., Fischer G., 2007. Reducing climate change
impacts on agriculture: Global and regional effects of
mitigation, 2000-2080. Technological Forecasting and
Social Change, 74 (7): 1030-1056
WDPA Consortium, 2004. World Database on Protected
Areas. Copyright World Conservation Union (IUCN)
and UNEP-World Conservation Monitoring Centre.
World Bank, 2005. World Development Indicators. World
Bank.
AN APPROACH TO MODELING LANDUSE CHANGE AND FOREST MANAGEMENT ON A GLOBAL SCALE
185