DEPIVOT – A SOFTWARE PACKAGE TO DESIGN

AND EVALUATE CENTER-PIVOT SYSTEMS

M. I. Valín

1,2

, M. R. Cameira

, C. Pedras

1,3

, P. R. Teodoro

, J. M. Gonçalves

1,4

and L. S. Pereira

Biossystems Engineering Research Center, Institute of Agronomy, Technical University of Lisbon

Tapada da Ajuda, 1349-017, Lisbon, Portugal

Agricultural College, Viana do Castelo Polytechnic Institute

Refóios do Lima, 4990-706, Ponte de Lima, Portugal

University of Algarve, Campus de Gambelas, 8005-139, Faro, Portugal

Agricultural College, Coimbra Polytechnic Institute, 3040-316, Coimbra, Portugal

Keywords: Hydraulics design, Sprinkler chart, Database, Performance indicators.

Abstract: This paper presents a simulation model aimed at center-pivot design and support assessing the performance

of systems under operation: DEPIVOT (Design and Evaluation of center PIVOT). The software code was

developed in Visual Basic and includes an Access database. DEPIVOT allows considering performance

criteria for design and to iteratively search better system solutions. The model has two main components: A.

the design of new systems and B. the evaluation of operating systems. The first component starts with the

agronomic design aiming the calculation of the system flow rate; this is followed by the hydraulic design:

(a) computes friction head losses along the lateral; (b) the creation of the sprinkler chart; and (c) the

validation of the sprinkler chart. The second component requires field data to calculate performance

indicators, such as distribution uniformity (DU) and the coefficient of uniformity (CU).

1 INTRODUCTION

Irrigation modelling allows the simulation of the

water distribution by an irrigation system under real

working conditions. Models have been developed in

order to avoid laborious field tests and to design and

improve irrigation systems. Montero et al. (2001)

consider that using a simulation model enables to

reduce water and energy consumption and increases

the efficiency of utilization of these resources.

Center-pivot systems have experienced a wide

diffusion because of its advantages relative to other

irrigation systems such as: 1) high potential for

uniform and efficient water applications, (Qassim et

al., 2008); 2) high degree of automation, (Al-

Kufaishi et al., 2006); and 3) ability to economically

and environmentally apply water and nutrients over

a wide range of soil, crop and topographic

conditions. Center pivot design models have been

reported in the literature for the last fifty years.

Heermann and Heid (1968) developed a model

based on Bittinger and Longenbaugh (1962), which

computed depth, rate, and uniformity of application

along the lateral, when the discharge and wetted

diameter at each sprinkler are specified. James

(1982) investigated the effects of topography on

water distribution and Allen (1989) developed a

program, USUPIVOT, where the user can input

infiltration rate parameters (surface storage,

infiltration pattern, and seal factor), crop parameters

(Etc), irrigation system parameters (working hours

and lateral radius), and the sprinkler pattern

(triangular and elliptic). Heermman et al., (1990)

simulated water distribution along the system

introducing new profiles with a donut design for low

pressure sprinklers. Bremod and Molle (1995) have

considered the pivot discontinuous motion,

determined sprinkler distribution pattern in

laboratory and calculated the water depth received in

each point. Other models have introduced the

calculus of runoff and soil loss in different soils

watered by the same system (Silva, 2006).

This paper presents a software package

(DEPIVOT) to use for the design of center-pivot

systems and for the assessment of the performance

of systems under operation or being designed.

DEPIVOT simulates different sprinkler charts for

the same system configuration and estimates runoff

298

Valín M., Cameira M., Pedras C., Teodoro P., Gonçalves J. and Pereira L..

DEPIVOT – A SOFTWARE PACKAGE TO DESIGN AND EVALUATE CENTER-PIVOT SYSTEMS.

DOI: 10.5220/0003610402980301

In Proceedings of the 6th International Conference on Software and Database Technologies (ICSOFT-2011), pages 298-301

ISBN: 978-989-8425-77-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

for each of them. This option allows to compare the

different sprinkler charts based on water

conservation criteria.

2 MODELING APPROACH

Fig. 1 shows the conceptual structure of the

DEPIVOT software. The software code was

developed in Visual Basic 6.0 and includes a

database in Access. The model has two main

components: A. design of new systems and B.

evaluation of operating systems. The first

component starts with the agronomic design aiming

the calculation of the system flow rate; being

followed by the hydraulic design; and the validation

of the sprinklers chart. The second component uses

field data to calculate the performance indicators,

Distribution Uniformity (DU) and Uniformity

Coefficient (UC) (Pereira and Trout, 1999).

Figure 1: Conceptual structure of the DEPIVOT software.

In the hydraulic design the user makes a first

selection of the span diameter, length and outlet

spacing. Considering the span with a continuous

flow rate (Keller and Bliesner, 1990; Scaloppi and

Allen, 1993) the friction head losses along the lateral

are determined in order to select the adequate

diameter, length and outlet spacing for all the spans.

The most important step of a center pivot design

is the creation of the sprinkler chart. To choose the

most suitable sprinkler for each outlet is necessary to

calculate the type, working pressure and the flow

rate at that point (sprinkler chart). To achieve this

the friction head loss is computed by the stepwise

method, which calculates friction losses in each pipe

length between two consecutive outlets.

The input data required for the calculation of the

required discharge (qi) and pressure (pi) for each

output are the same as those used for span selection,

plus the distance between outlets. The q

is the one

that produces the best uniformity along the lateral

and also the ideal pressure (p

Starting form q

, the sprinklers charts can be

obtained directly by the user, manual chart, or by the

model through an optimized automatic approach.

With the first option, the model runs a query to the

database and shows all sprinklers. The user chooses

the sprinkler and the model calculates and shows the

actual discharge as a function of the pressure in that

point. If the optimized sprinkler chart option is

selected, the model, starting at the first outlet,

chooses the sprinkler whose discharge is the nearest

to the required discharge (q

, L s

-1

). Afterwards, it

calculates the friction head losses section-by-section

f i,i+1

), thus obtaining the actual pressure (p

ai+1

) at

each outlet as the result of the pressure in the

previous output minus the friction head losses and

the difference in elevation between consecutive

outlets (Figure 2). The flow rate is then calculated

ai+1

) by the discharge-pressure function. The model

runs a new query to the database, being the cycle

repeated for every outlet. The model allows the

storage of several possible sprinkler charts for the

lateral.

Figure 2: Iterative computation of pressure (P

, kPa) and

discharge (q

, ls

-1

) for each outlet i.

Each sprinklers chart can be validated using two

criteria: i) performance indicators; and ii) runoff

calculations. At the sprinkler level, two performance

indicators, the Distribution Uniformity (DU) and the

Uniformity Coefficient (UC) are calculated. For the

second validation the model calculates the potential

runoff (P

, mm) for each sprinkler chart selected

previously by comparing the application (P) and

infiltration rate curves (i) as function of time (t).

The DEPIVOT database was developed with

Microsoft Access and can be updated whenever

required. It stores the equipment (sprinklers and

spans) available in the market and the results

(information relating to projects created or

evaluated). For each nozzle inserted in the database,

it is necessary to enter the pairs of maximum and

minimum values of pressure and flow recommended

by the manufacturer. This allows: i) limiting the

operating range of the sprinkler; and ii) calculating

the coefficients k

and x to be stored and used to

Start

Desi gn new

syste

Hydraulic

simulation

Va lid at ion of

emitter chart

End

Evaluation of

operating systems

Input data field

Computation of

perfor mance

indicators

Emitter Chart

Gross

irrigation

requirements

Sp a ns

Em it ters

Systems

f i,i+1

) P

ai + 1

- h

f i,i+1

- (z

i+1

- z

)

ai+1

)

DEPIVOT - A SOFTWARE PACKAGE TO DESIGN AND EVALUATE CENTER-PIVOT SYSTEMS

299

calculate the flow rate associated to the pressure

supplied.

3 RESULTS

The model initiates with two options: design of a

new system or evaluation of an operating system.

After choosing the option Design a new system

DEPIVOT allows the user to introduce the system

flow rate as an input or to request the model to use

an algorithm to calculate it by the soil water balance.

This algorithm is feed manually or by importing

WinISAREG model output file to calculate the crop

irrigation requirements.

Once the system flow rate is defined, the user

begins the hydraulic simulation. The user introduces

the system characteristics and selects diameter (D,

mm) and length (L, m) of the span from the

database, including the spacing between outlets (Se,

mm). Selection of all spans is made trough database

consulting, where the equipment characteristics were

previously introduce. The model allows the

installation of a gun in the distal end. If the total

friction losses, is higher than 15% of the working

pressure, a message is displayed indicating the need

to select a different span. The program simulates a

static position for the system, therefore the user must

decide previously which is the most representative

position in terms of the field slope.

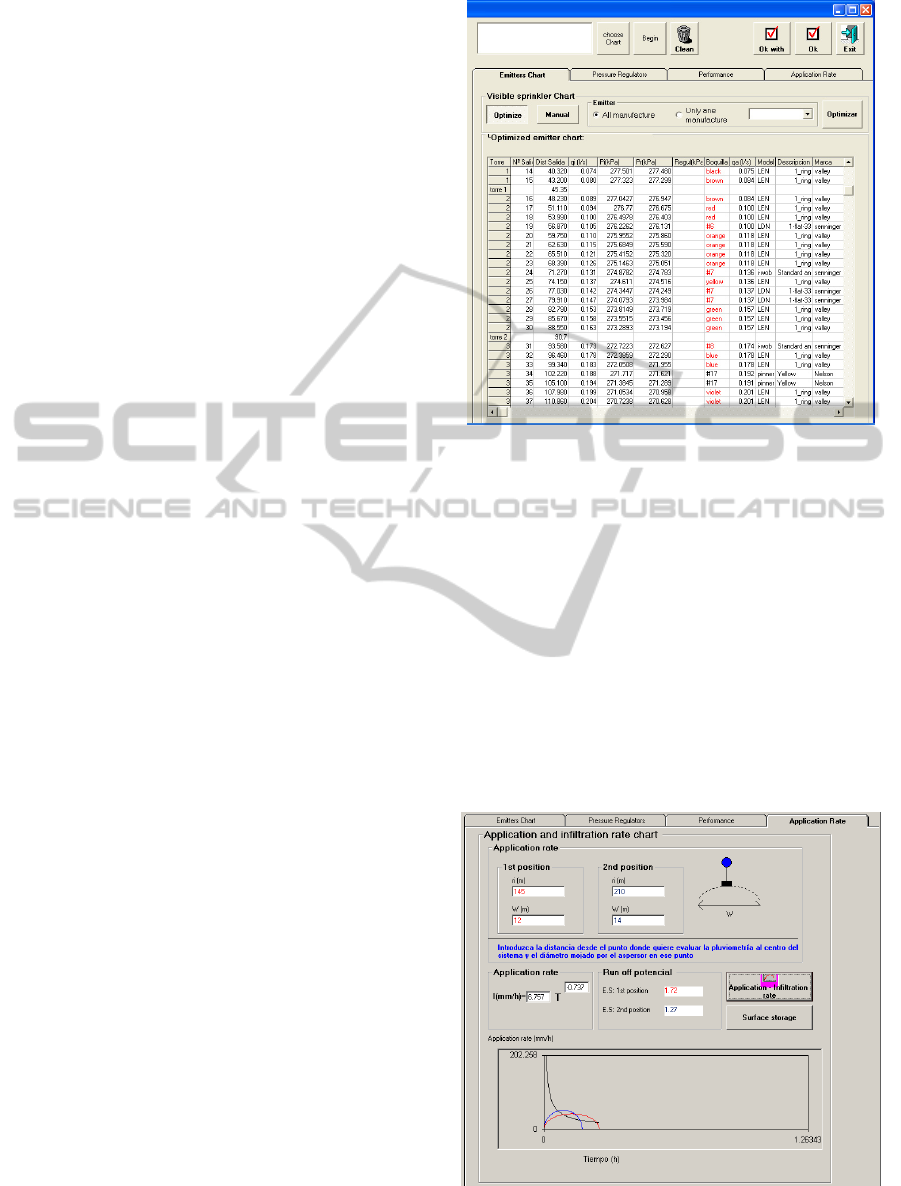
Once the spans are sized, the sprinklers chart is

defined. The sprinklers’ characteristics are acceded

in a specific database. The sprinklers chart (Figure

3) includes for each outlet: the radial distance (ri);

the required discharges (qi) and actual discharges

(qa); the required pressure (Pi) and actual pressure

(Pa); and the identification of sprinklers

(manufacture, model, description and nozzle).

Sprinkler’s selection can be carried out for a given

manufacturer or within the entire database. The

selection may be optimized by the model by

searching, for each outlet i, located at the radial

distance ri from the pivot, the sprinklers that produce

a discharge qai that is the closest to the required one

qi if the available outlet pressure is Pi. In alternative,

the selection may be done by the user, option

Manual. This option allows i) to choose one of the

charts created and individually change each

sprinkler (within a range of 10% of the discharge)

and ii) create a new sprinkler chart that allows to

choose any sprinkler existing in the database. Once

this selection is completed, the sprinkler pressure

and discharge are computed by the iterative process

(Fig. 3).

Figure 3: Window for design the sprinklers chart at each

lateral.

The model allows the association of several

sprinkler charts to each system, to modify them and

store it with different names. Figure 3 shows in red

ink the nozzles that work above the pressure defined

by the manufacturer in the database. If the user

chooses to install pressure regulators its selection is

supported by an additional window where the user

decides in which span should the regulators be

installed and which is the regulating pressure

(PRmax). The model updates the pressure values

and allocates them in column Regul (kPa) in the

sprinklers chart as the pressure used for calculating

the flow rate.

Figure 4: Window for estimating potential runoff and

surface storage.

ICSOFT 2011 - 6th International Conference on Software and Data Technologies

300

The potential runoff computation is supported by

the window shown in Figure 4. Results for potential

runoff are shown graphically and numerically for

two positions. By pressing the button Aplication –

infiltration rate the model presents a dialog box to

insert the number of hours needed for a complete

revolution.

When the model is used to evaluate a system

under operation, first the common data to all

evaluations are introduced (equipment´s

characteristics); second the water depths caught in

catch cans placed along two radius are used to

compute DU and UC. Results are presented in

numerical and graphical formats.

4 CONCLUSIONS

DEPIVOT model is oriented to find solutions for the

critical aspects that limit achieving good

performances in the farmer irrigation practice.

Particular attention has been given to: determining

the irrigation water requirements and the

corresponding system discharge; sizing of the lateral

in order to achieve an adequate variation of pressure;

producing the sprinklers charts; determining the

functioning conditions for every sprinkler;

estimating the runoff potential; and defining the

main information for system management in

practice. The model is presented in WINDOWS

environment, with a structure between windows and

with a set of databases that can be consulted and

altered from the model itself. Once developed, the

model has been tested with results of field

evaluations. These results show that the model is

able to respond to the objectives that led to its

development, which are to assist farmers and

technicians in selecting and designing new centre-

pivot systems and to identify operational

performance problems and respective solutions.

ACKNOWLEDGEMENTS

The support by CEER - Biosystems Engineering

(POCTI/U0245/2003) and the research project

PTDC/AGR-AAM/105432/2008 funded by

Portuguese Foundation for Science and Technology

are acknowledged.

REFERENCES

Allen, R. G., 1989. USUPIVOT: Center pivot nozzle

selection computer software user´s manual.

Department of Agriculture and Irrigation Engineering,

Utah State University, Logan, Utah, 15.

Al-Kufaishi, S. A.,·Blackmore, B. S., H. Sourell 2006.

The feasibility of using variable rate water application

under a central pivot irrigation system. Irrig Drainage

Syst 20:317–327.

Bittenger, M., W., Logenbraugh, R. A., 1962. Theoretical

distribution of water from a moving irrigation

sprinkler", Transactions of the ASAE 5(1): 26-30

Bremond B., Molle, B., 1995. Characterization of rainfall

under centre pivot. Influence of measuring procedure.

Journal of Irrigation and Drainage Engineering ASCE

121 (5): 347 – 353

Heermann, D. F., Hein, P. R., 1968. Performance

characteristics of self-proped center-pivot sprinkler

irrigation system. Transactions of the ASAE 11(1): 11-

Heermann, D. F., Wallender, W. W., Bos, G. M, 1990.

Irrigation eficiency and Uniformity. In: Hoffman, G.

J., Howell, T. A., Solomon, K. H. (Eds.), Management

of Farm Irrigation Systems. ASAE, St. Joseph, MI,

125 -149.

James, L. G., 1982. Modeling the performance of center

pivot irrigation systems operating on variable

topography. Transactions of the ASAE 38(1): 143-149.

Keller, J. y Bliesner, R. D., 1990. Sprinkle and Trickle

Irrigation Van Nostrand Reinhold. New York.

Montero, J., Tarjuelo, J. M., Carrión, P. 2001. Nueva

versión del modelo de simulación de riego por

aspersión SIRIAS. In: XIX Congreso Nacional de

Riegos, AERYD, Madrid, CD-ROM paper C-18.

Pereira, L. S., Trout T. J., 1999. Irrigation Methods. In:

HN van Lier, LS Pereira, FR Steiner (Eds.) CIGR

Handbook of Agricultural Engineering, Vol. I: Land

and Water Engineering, ASAE, St. Joseph, MI, pp.

297-379

Qassim, A., Dunin F., Bethume M. (2008). Water balance

of center pivot irrigated pasture in northern Victoria,

Australia. Agric. Water Manag. 95, 566-574

Scaloppi E. J., Allen R., 1993. Hydraulics of Center-Pivot

laterals. Journal of Irrigation and Drainage

Engineering ASCE 119 (3): 554-567

Silva, L. S. (2006) The effect of spray head sprinklers with

different deflector plates on irrigation uniformity,

runoff and sediment yield in a Mediterranean soil.

Agric. Water Manag. 85, 243-252

DEPIVOT - A SOFTWARE PACKAGE TO DESIGN AND EVALUATE CENTER-PIVOT SYSTEMS

301