
INTERNATIONALLY STANDARDIZED EFFICIENT
CRYPTOGRAPHIC HASH FUNCTION
Danilo Gligoroski, Svein Johan Knapskog
Department of Telematics, Q2S, Norwegian University of Science and Technology, Trondheim, Norway
Jørn Amundsen, Rune Erlend Jensen
Department of Computer and Information Science, Norwegian University of Science and Technology, Trondheim, Norway
Keywords:
Information security, Cryptographic hash functions, International standardization.
Abstract:
We claim that the European research and development community can initiate and sustain a process of de-
signing a secure cryptographic hash function that will be widely accepted by the industry due to its superior
performances in software compared to any of the hash functions MD5, SHA-1, SHA-2 or SHA-3.
We base our claim on three main arguments: 1. The industry demands very fast cryptographic hash functions
due to the increased volume of information that needs to be processed in a secure way. 2. The current trends
of increased degree of instructional level parallelism and development of vector extensions of recent CPUs
have a potential for being efficiently exploited by new cryptographic hash designs. 3. The list of the SHA-3
finalists does not contain algorithms which are significantly faster than SHA-2.
1 INTRODUCTION
The three most important pillars in the modern cryp-
tology and information security are cryptographic
hash functions, modern block ciphers and the concept
of public key cryptography.
Beside the main use of cryptographic hash func-
tions as a pivotal part of existing digital sig-
nature schemes (IEEE-SA-Standards-Board, 2000;
ISO/IEC, 2006; NIST, 2009; ANSI, 1998), there are
dozens of other security techniques where use of the
properties of the cryptographic hash function are in-
dispensable, and many more new algorithms, proto-
cols and schemes are still being invented.
The basic motivation for constructing a hash func-
tion is to implement functionality which will pro-
duce a check value (fingerprint) uniquely represent-
ing a digital file. Loosely speaking, the request for
the uniqueness of the check values is a two-fold re-
quest: the cryptographic hash function should be one-
way, and it should be collision free. Beside that, the
length of the check values represented as a binary
string should be small enough in order to efficiently
store them and to easily manipulate them. The check
value size (sometimes called the hash size, or the di-
gest size) normally range from 128 to 512 bits.
The practical requirements for a cryptographic
hash function H() can be described by these require-
ments:
One-way: The cryptographic hash function H() has
to be “one-way” from two perspectives:
Preimage Resistant: It should have the property
that it is “easy” to compute H(M) = h for a
given M, but it should be “hard” (or “infea-
sible”) to compute M if just the value of h is
given.
Second Preimage Resistant: It should have the
property that for a given M
1
it is “easy” to com-
pute H(M
1
) = h, but it should be “hard” (or
“infeasible”) to find another M
2
6= M
1
such that
H(M
2
) = H(M
1
) = h.
Collision Resistance: The cryptographic hash func-
tion should be “collision resistant” i.e., it should
be “hard” (or “infeasible”) to find two values
M
1
6= M
2
such that H(M
1
) = H(M
2
).
An extensive (but far from complete) list of appli-
cation of cryptographic hash functions:
426
Gligoroski D., Johan Knapskog S., Amundsen J. and Erlend Jensen R..
INTERNATIONALLY STANDARDIZED EFFICIENT CRYPTOGRAPHIC HASH FUNCTION.
DOI: 10.5220/0003611604260433
In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2011), pages 426-433
ISBN: 978-989-8425-71-3
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
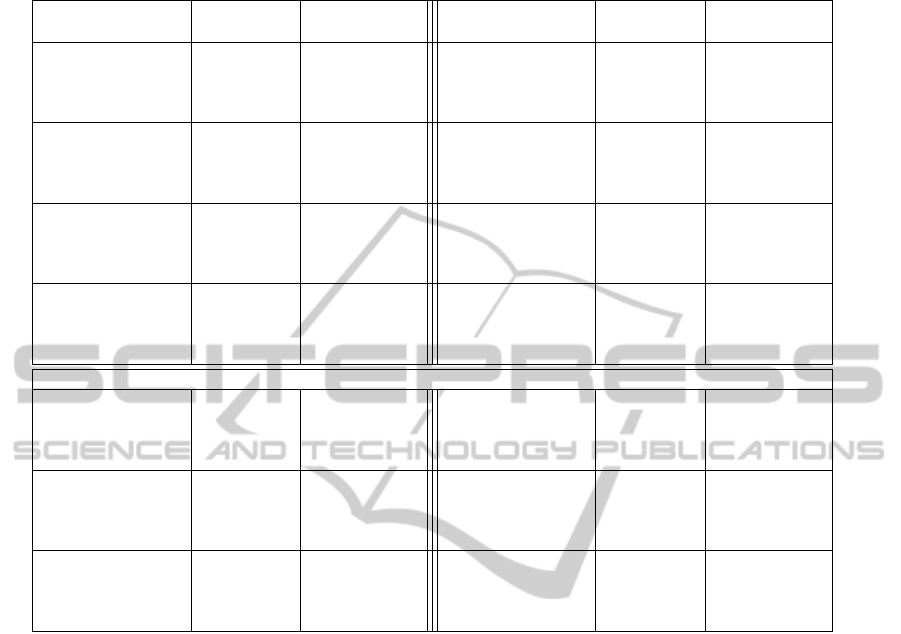
Table 1: A list of applications where hash functions are used. The list was composed from diverse Internet sources, crypto-
graphic forums and the hash mailing list.
Application in
Used hash
functions
Use frequency Application in
Used hash
functions
Use frequency
Digital signatures
MD5 Rare
Data Integrity
MD5 High
SHA-1 High SHA-1 Modest
SHA-256 Rare SHA-256 Rare
SHA-512 Rare SHA-512 Rare
Commitment schemes
MD5 Modest
Password protection
MD5 High
SHA-1 High SHA-1 High
SHA-256 Rare SHA-256 Modest
SHA-512 Rare SHA-512 Rare
Microsoft CLR strong
names
MD5 None
Python setuptools
MD5 High
SHA-1 High SHA-1 High
SHA-256 Rare SHA-256 Modest
SHA-512 Rare SHA-512 Rare
Software packet
managers
MD5 High
Google micropayment
system
MD5 None
SHA-1 High SHA-1 High
SHA-256 Modest SHA-256 None
SHA-512 Rare SHA-512 None
Security mechanism for
Local file systems
MD5 High
Decentralized file
systems
MD5 High
SHA-1 High SHA-1 High
SHA-256 Rare SHA-256 Rare
SHA-512 Rare SHA-512 Rare
P2P file-sharing
MD5 High
Decentralized revision
control tools
MD5 High
SHA-1 High SHA-1 High
SHA-256 Rare SHA-256 Rare
SHA-512 Rare SHA-512 Rare
Intrusion detection
systems
MD5 High
De-duplication
systems
MD5 High
SHA-1 High SHA-1 High
SHA-256 Rare SHA-256 Rare
SHA-512 Rare SHA-512 Rare
2 THE CURRENT STATUS OF
THE MOST USED
CRYPTOGRAPHIC HASH
FUNCTIONS
The concept of a cryptographic hash function is rela-
tively new. The first explicit note for the need of one-
way functions in cryptography was given by Diffie
and Hellman in 1976 (Diffie and Hellmann, 1976) and
was followed by several significant theoretical works
by Yao in 1982 (Yao, 1982) and Levin in 1987 (Levin,
1987) where the existence of one-way functions was
connected with the famous question from the com-
plexity theory: “Is P = NP ?”
The first cryptographer who took on the hard task
to design a “cryptographic hash function” was Ron
Rivest back in the late 1980s by designing the first
hash function that was supposed to be preimage, sec-
ond preimage and collision resistant: MD2 (Kaliski,
1992). Then, in 1990 he designed MD4 (Rivest,
1990) and in 1992 MD5 (Rivest, 1992). His designs
inspired a whole family of designs, and that family of
hash designs are now known as MDx family. To that
family belong also hash functions HAVAL (Zheng
et al., 1992), RIPEMD (Bosselaers et al., 1997) and
many others. The historical fact is that as those hash
functionswere designed, cryptographerswere analyz-
ing them and were breaking them.
Then NSA came on the scene and they designed
Secure Hash Algorithm (SHA) (NIST, 1992) based
on MDx principles. That function was proposed for
standardization via NIST in 1993. While the digest
size of MDx hash functions was 128 bits, the size of
the SHA was increased to 160 bits. However, after
few years, NSA discovered a weakness in SHA and
promptly proposed a tweak. The original SHA is now
known as SHA-0 and the tweaked algorithm as it is
known today is SHA-1 (NIST, 2002).
Aware of the constant progress that public com-
munity was doing in cryptanalysis and breaking the
proposed cryptographic hash functions, NSA build
up a new hash function under the name SHA-2, and
NIST have adopted it as a standard in 2000 (NIST,
2002). In SHA-2, several new design principles were
INTERNATIONALLY STANDARDIZED EFFICIENT CRYPTOGRAPHIC HASH FUNCTION
427
introduced, and the digest size is increased to 224,
256, 384 or 512 bits.
In parallel with the standardization activities of
NIST and NSA, the European Union launched a
scientific project RIPE (RACE Integrity Primitives
Evaluation, 1988-1992) (Bosselaers et al., 1997) and
as a result of that project the cryptographic func-
tion RIPEMD-160 designed by H. Dobbertin, A.
Bosselaers and B. Preneel (Dobbertin et al., 1996).
RIPEMD-160 is also part of the ISO/IEC interna-
tional standard ISO/IEC 10118-3:2003 on dedicated
hash functions.
Despite the fact that RIPEMD-160 is considered
as cryptographically sound and unbroken function, its
broader use remains very low compared with MD5,
SHA-1 and SHA-2.
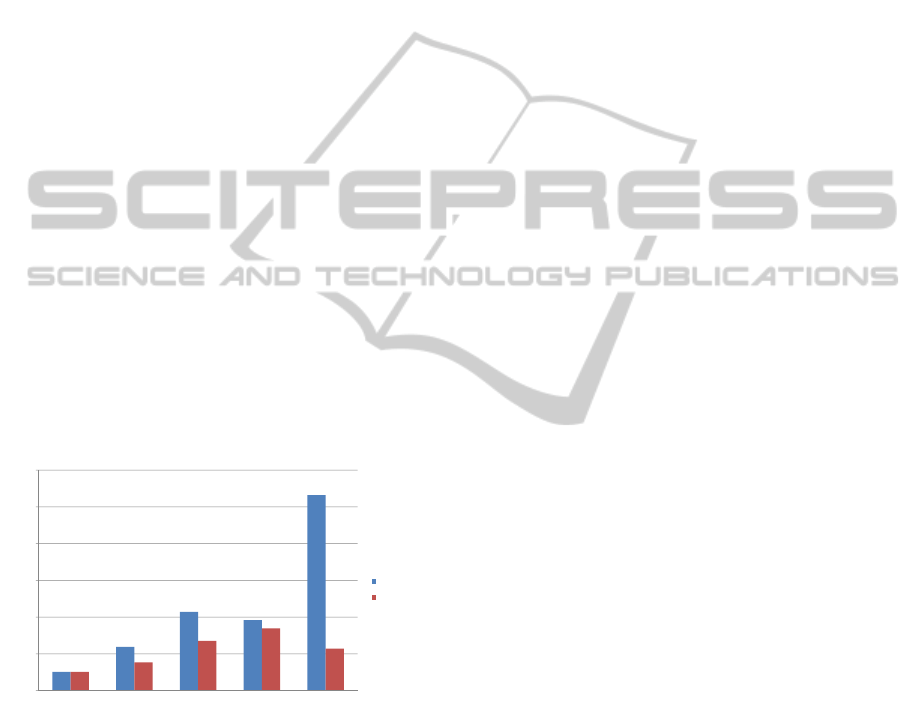
A simple comparison of the hash functions MD5,
SHA-1, RIPEMD-160, SHA-256 and SHA-512, run-
ning on a modern Intel Core i7-920XM CPU at 2.0
GHz both in 32-bit and 64-bit mode, performed with
the ECRYPT Benchmarking of Cryptographic Sys-
tems - SUPERCOP (Bernstein and Lange, 2011), is
given in Figure 1.
One can only speculate about the reasons why
RIPEMD-160 is not so frequently used as MD5 and
SHA-1. However, we will just point out that it is ap-
proximately 2 times slower than SHA-1 and between
3 and 4 times slower than MD5.
SUPERCOP measurements on Intel Core i7 920X, 2.0 GHz
60
53.18
50
e
40
byt per
30
s
32 bit!mode
cycle
64 bit!mode
21.45
19.17
16.97
20
CPU
13.55
11.9
11.45
5.07
11.9
21.45
19.17
53.18
5.09
7.66
13.55
16.97
11.45
0
10
20
30
40
50
60
MD5 SHA 1 RIPEMD 160 SHA 256 SHA 512
CPU cycles per byte
SUPERCOP measurements on Intel Core i7 920X, 2.0 GHz
32 bit!mode
64 bit!mode
Figure 1: Comparison of the speed of MD5, SHA-1,
RIPEMD-160, SHA-256 and SHA-512 (shorter bars are
better).
3 THE CURRENT STATUS OF
THE MOST USED
CRYPTOGRAPHIC HASH
FUNCTIONS
We commend NIST for their commitment to con-
stantly work on improving the information security.
So far they have accepted the challenges of the dif-
ficult task to organize worldwide cryptographic com-
petitions for the Advanced Encryption Standard and
for the Advanced Hash Standard. It is a general and
widely accepted opinion amongst the cryptographic
communitythat NIST has significantly stimulated and
motivated the research in cryptology and by this, they
have gained high reputation.
On the NISTs web page there is a brief summary
of the objectives and the process of the competition
from its announcement up to the recent decision for
the final Round 3 of the competition. We quote:
NIST announced a public competition (Federal
Register Notice) on Nov. 2, 2007 to develop a new
cryptographic hash algorithm, which converts a vari-
able length message into a short ”message digest”
that can be used in generating digital signatures, mes-
sage authentication codes, and many other security
applications in the information infrastructure. The
competition was NIST’s response to advances in the
cryptanalysis of hash algorithms. The winning algo-
rithm will be named ”SHA-3”, and will augment the
hash algorithms currently specified in the Federal In-
formation Processing Standard (FIPS) 180-3, Secure
Hash Standard.
NIST received sixty-four entries by October 31,
2008; and selected fifty-one candidate algorithms to
advance to the first round on December 10, 2008, and
fourteen to advance to the second round on July 24,
2009. A year was allocated for the public review of
the fourteen second-round candidates.
NIST received significant feedback from the cryp-
tographic community. Based on the public feedback
and internal reviews of the second-round candidates,
NIST selected five SHA-3 finalists - BLAKE, Grøstl,
JH, Keccak, and Skein to advance to the third (and
final) round of the competition on December 9, 2010,
which ended the second round of the competition.
3.1 A Cryptographic Competition with
Inconsistencies
In the initial NIST SHA-3 requirements (November
2, 2007) NIST issued a statement about the efficiency
of the next SHA-3 function: NIST expects SHA-3 to
have a security strength that is at least as good as
the hash algorithms currently specified in FIPS 180-
2, and that this security strength will be achieved with
significantly improved efficiency.
However, NIST did not define more precisely
what the phrase “with significantly improved effi-
ciency” means. Several cryptographers like Fleis-
chmann, Forler and Gorski in (Fleischmann et al.,
2008) defined performance classes and classified the
SECRYPT 2011 - International Conference on Security and Cryptography
428

hash algorithms accordingly. There, the class with the
closest meaning to the phrase “with significantly im-
proved efficiency” is the class of hash functions that
are at least two times faster than SHA-2. We agree
with their classification.
As time progressed during the first and the sec-
ond phase of the competition we witnessed a shift
in the NIST claims. On June 4, 2010, William E.
Burr, the manager of the Cryptographic Technology
Group at NIST wrote to the hash forum list: We can
have a legitimate argument about which applications
are the most demanding and most important, but if
we don’t have an algorithm that is competitive with
SHA-2 in the conventional business computation plat-
forms where most commercial applications run, then
it’s hard to see how SHA-3 is going to displace SHA-
2. I think that SHA-2 is looking like a better perform-
ing, more efficient set of algorithms than I had ex-
pected, so at least matching SHA-2 in most cases,
and being much better at others is a pretty high bar.
We see that statement as the justification for their
final decision made on December 9, 2010 when NIST
selected the five SHA-3 finalists BLAKE, Grøstl, JH,
Keccak, and Skein to advance to the third (and fi-
nal) round of the competition. The evaluation per-
formed on ECRYPT Benchmarking of Cryptographic
Systems - SUPERCOP (Bernstein and Lange, 2011)
on Intel Core i7 920X CPU running at 2.0 GHz is
shown in Table 2 and Table 3.
Table 2: Comparison of the speed of the five SHA-3 final-
ists with security parameters equivalent to SHA-512-256.
The yellow color is for the reference function SHA-512-
256, while the pink color denotes slower functions, and the
red color denotes significantly slower functions.
64-bit mode, 256 bit hash
Name
Speed
cycles/byte
1. Skein-512-256 6.25
2. BLAKE256 8.52
3. SHA-512/256 11.45
4. Keccak512 12.34
5. JH256 16.53
6. Grøstl256 21.94
We see from Table 2 and Table 3 that only two
functions are faster, but not significantly faster than
SHA-2. If we take into consideration that on the same
platform the speed of MD5 is 5.1 cycles per byte and
that of SHA-1 is 7.66 cycles per byte, we can again
support our assumption that in the forthcoming period
of the next 10 – 20 years the industry will continue to
use the much less safe MD5 and SHA-1, due to the
fact that SHA-2 and possibly SHA-3 will continue to
be much slower.
Table 3: Comparison of the speed of the five SHA-3 finalists
with security parameters equivalent to SHA-512. The yel-
low color is for the reference function SHA-512-256, while
the pink color denotes slower functions, and the red color
denotes significantly slower functions.
64-bit mode, 512 bit hash
Name
Speed
cycles/byte
1. Skein-512-256 6.25
2. BLAKE512 10.15
3. SHA-512 11.45
4. JH512 16.61
5. Keccak1024 22.78
6. Grøstl512 32.31
3.2 Increased Knowledge about the
Designing Principles for Iterated
Hash Functions
During the period of the last 3 years, i.e. since the start
of the SHA-3 competition, the cryptographic commu-
nity have deepened their understanding of the design
principles of iterated hash functions (MD design).
Bart Preneel has summarized this in his talk given at
the Twelfth International Conference on Information
and Communications Security ICICS 2010 (Preneel,
2010). Now, we have learned that an improved MD
design should include the following parts:
Salt + Output transformation + Counter + Wide pipe.
Further on, Preneel discussed about the possibility
of a new SHA-4 competition emphasizing the follow-
ing points:
• an open competition such as SHA-3 is bound to
result in new insights between 2008-2012.
• only few of these can be incorporated using
“tweaks”.
• the winner selected in 2012 will reflect the state
of the art in October 2008.
• nevertheless, it is unlikely that we will have a
SHA-4 competition before 2030.
We agree that a new SHA-4 competition is un-
likely to be organized before 2030. However, it is pos-
sible to organize a European initiative, based on our
newly gained knowledge, to develop highly efficient
cryptographic hash functions in close cooperation be-
tween the academic research communities, industry
and the standardization organizations.
INTERNATIONALLY STANDARDIZED EFFICIENT CRYPTOGRAPHIC HASH FUNCTION
429
4 USE CASE SCENARIOS WITH
DIFFERENT DIGITAL
SIGNATURES SCHEMES AND
DIFFERENT HASH
FUNCTIONS
A test case using cryptographic hash functions for
signing and verification of digital signatures used in
the DICOM standard (Digital Imaging and Commu-
nications in Medicine) (NEMA, 2001) especially in
real-time teleradiology and mammography, has been
performed. There, the speed of the hash function is
the real bottleneck, taking even up to 99.7% of the
time spent on signing or verification. We demonstrate
how the speed of hash functions becomes a compu-
tational bottleneck by producing digital signatures on
files with average sizes starting from 16 KB (typical
PDF files in financial transactions) up to files with a
size of 10 MB. Note that the modern mammographic
scanners produce even much bigger images - up to
160 MB. Additionally from the same perspective we
present a what-if analysis that includes several new
cryptographic hash functions from the ongoing SHA-
3 competition.
We have performed an extensive set of experi-
ments testing several attributes that are described in
the Fig. 2. For the testing environment we have used
the ECRYPT Benchmarking of Cryptographic Sys-
tems - SUPERCOP (Bernstein and Lange, 2011). SU-
PERCOP is a toolkit developed by the VAMPIRE lab
for measuring the performance of cryptographic soft-
ware. For our purposes we have modified the signing
routines that are in SUPERCOP not only to work with
SHA-1 or SHA-256 but with different hash functions
and not only on files up to 97KB, but to files up to
10MB. Our measurements were produced on a ma-
chine with Intel Core i7-920XM, running at 2.0 GHz
in 64-bit mode.
Security level
(power of 2)
80 92 112 128
RSA 1024 1536 2048 3072
ECDSA 160 192 224 256
x
Key generation
x
Signing
x
Verification
x
File size
0 16K 32K 64K 128K 256K 512K 1M 4M 10M
x
Hash functions
BMW512, Edon!R512, SHA!256, SHA!512, Shabal512, Skein51
2
Figure 2: Multidimensional testing setup for our perfor-
mance measurements.
We have performed extensive tests of signing and
verification, covering all possibilities for the security
levels and file sizes up to 10M, but due to the space
constrains in this paper we will present the findings
for RSA1536 and ECDSA192.
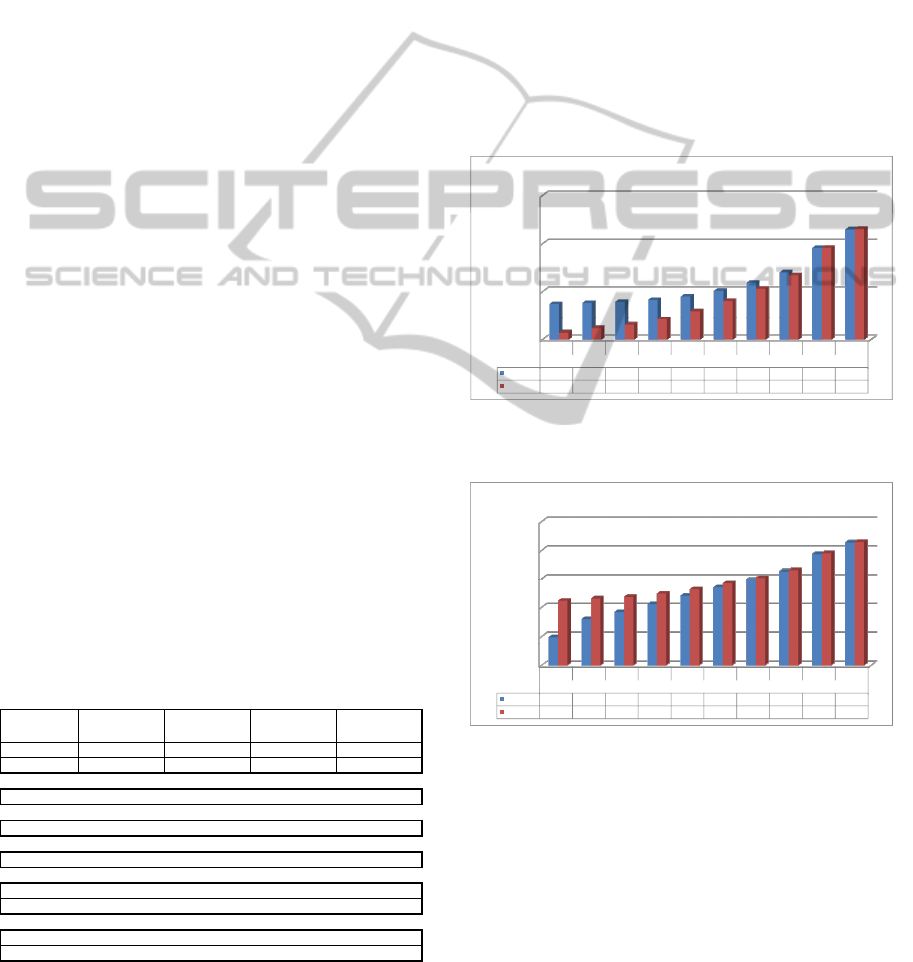
In Fig. 3 and Fig. 4 we present measurements
performed with RSA1536 and ECDSA192 where the
used hash function was SHA-256. There are signifi-
cant speed differences between RSA and ECDSA but
they disappear as the file size increases. For exam-
ple for short files, ECDSA192 is up to 4 times faster
in signing and up to 18 times slower in verification
compared to RSA1536. However for files larger then
256 KB, the factor of that speed imbalance falls below
1.3, and for files bigger than 4M the speed is almost
the same.
Signing time (file size from 0 to 10M)
1.00E+09
1.00E+06
1.00E+07
1.00E+08
1.00E+09
0 16K 32K 64K 128K 256K 512K 1M 4M 10M
Length of the signed file
RSA1536
5.51E+06 5.80E+06 6.10E+06 6.70E+06 7.87E+06 1.02E+07 1.50E+07 2.44E+07 8.12E+07 1.95E+08
ECDSA192
1.40E+06 1.71E+06 2.03E+06 2.65E+06 3.90E+06 6.38E+06 1.14E+07 2.14E+07 8.16E+07 2.02E+08
CPU cyc les
Signing time (file size from 0 to 10M)
Figure 3: Comparison between RSA1536 and ECDSA192
speed of signing messages with different sizes.
Verification time (file size from 0 to 10M)
1.00E+09
1.00E+08
1.00E+07
escycl
1.00E+06
CPU
1.00E+05
1.00E+04
0 16K 32K 64K 128K 256K 512K 1M 4M 10M
Length of the signed file
RSA1536
9.30E+04 3.88E+05 6.80E+05 1.27E+06 2.44E+06 4.79E+06 9.49E+06 1.90E+07 7.61E+07 1.90E+08
ECDSA192
1.66E+06 1.97E+06 2.25E+06 2.92E+06 4.10E+06 6.61E+06 1.15E+07 2.14E+07 8.10E+07 2.00E+08
Signing time with ECDSA192 vs hashing time with SHA256
90 0%
1.00E+04
1.00E+05
1.00E+06
1.00E+07
1.00E+08
1.00E+09
0 16K 32K 64K 128K 256K 512K 1M 4M 10M
Length of the signed file
RSA1536
9.30E+04 3.88E+05 6.80E+05 1.27E+06 2.44E+06 4.79E+06 9.49E+06 1.90E+07 7.61E+07 1.90E+08
ECDSA192
1.66E+06 1.97E+06 2.25E+06 2.92E+06 4.10E+06 6.61E+06 1.15E+07 2.14E+07 8.10E+07 2.00E+08
CPU cyc les
Verification time (file size from 0 to 10M)
Signing time with ECDSA192 vs hashing time with SHA256
Figure 4: Comparison between RSA1536 and ECDSA192
speed of verification of signatures for messages with differ-
ent sizes.
The reason for the noticed disappearance of the
speed imbalance between RSA and ECDSA as the file
size increase is the computation of the hash digest of
the files. It is best viewed in Fig. 5 and Fig. 6.
By having this apparent dependence of the speed
of the used hash function it is a logical question to
see how the speed of the hash function will affect the
performance of the whole process of producing sig-
natures and their verification.
SECRYPT 2011 - International Conference on Security and Cryptography
430
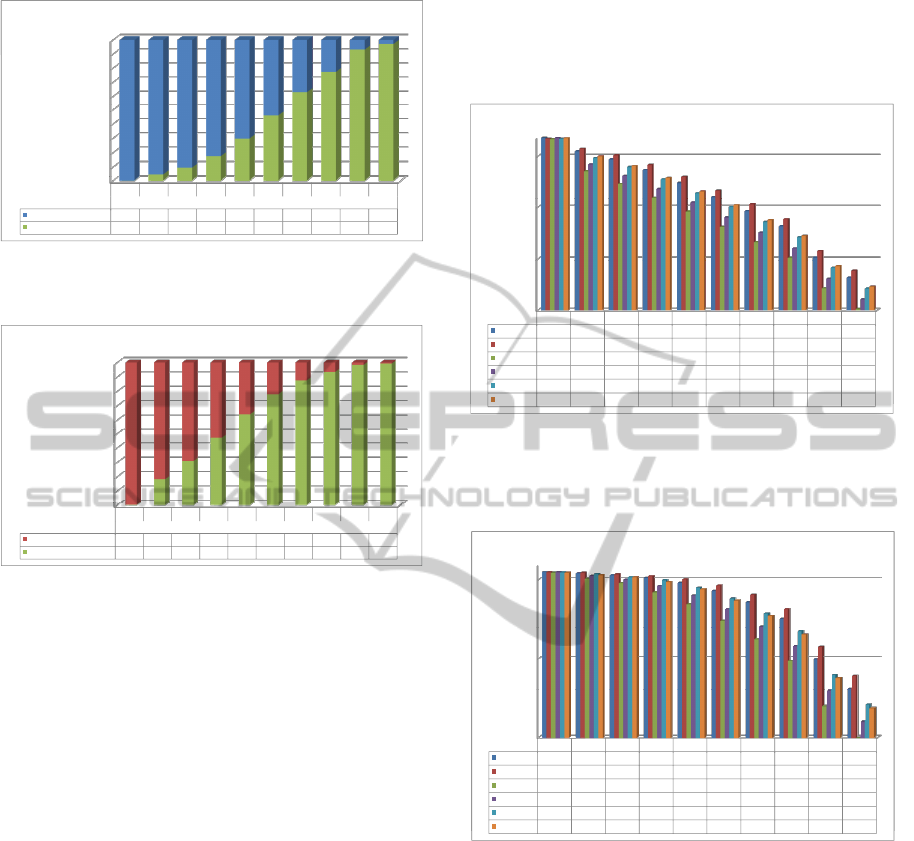
90 00%
100.00%
Signing time with RSA1536 vs hashing time with SHA256
0.00%
10.00%
20.00%
30.00%
40.00%
50.00%
60.00%
70.00%
80.00%
90.00%
100.00%
0 16K 32K 64K 128K 256K 512K 1M 4M 10M
Length of the signed file
RSA1536 Signing
99.97% 95.0% 90.4% 82.3% 70.0% 53.8% 36.8% 22.6% 6.8% 2.8%
RSA1536 SHA256 Hashing
0.03% 5.0% 9.6% 17.7% 30.0% 46.2% 63.2% 77.4% 93.2% 97.2%
CPU cycles
Signing time with RSA1536 vs hashing time with SHA256
Figure 5: Distribution of signing and hashing times for
RSA1536 performed by SHA-256.
Signing time with ECDSA192 vs hashing time with SHA256
100.0%
90 0%
0.0%
10.0%
20.0%
30.0%
40.0%
50.0%
60.0%
70.0%
80.0%
90.0%
100.0%
0 16K 32K 64K 128K 256K 512K 1M 4M 10M
Length of the signed file
ECDSA192 Signing
99.9% 81.7% 69.1% 52.9% 35.9% 21.9% 12.3% 6.5% 1.7% 0.7%
ECDSA192 SHA256 Hashing
0.1% 18.3% 30.9% 47.1% 64.1% 78.1% 87.7% 93.5% 98.3% 99.3%
CPU cycles
Signing time with ECDSA192 vs hashing time with SHA256
Figure 6: Distribution of signing and hashing times for
ECDSA192 performed by SHA-256.
We have adopted the recommendations given in
the recently published draft US standard FIPS 180-
4 using versions of SHA-512 for producing message
digests of 224 and 256 respectively on 64-bit proces-
sors. Thus, we decided to test two variants of SHA-
2 (SHA-256 and SHA-512) and the fastest four hash
functions in 64-bit mode of operation submitted to
the NIST SHA-3 competition: Blue Midnight Wish
(Gligoroski et al., 2009), Edon-R (Gligoroski et al.,
2008), Shabal (Bresson et al., 2008) and Skein (Fer-
guson et al., 2009). All of the mentioned SHA-3
candidates as well as SHA-512 are much faster than
SHA-256 in 64-bit mode of operation.
As expected, for short messages the performance
does not differ too much with any of the used hash
functions, but for longer file sizes the speed of the
hash function has significant effect. In Fig. 7 and
Fig. 8 we present our measurements for the verifi-
cation speed of RSA1536 and ECDSA192 with dif-
ferent hash functions. The numbers are expressed as
number of verifications that one CPU core can per-
form in one second. This methodology make sense
if we are planning to install our signing/verification
software in an organization server that has to per-
form a lot of signing and verification operations (as
described in (Menasce’, 2003)).
As can be seen in Fig. 7 and Fig. 8 for bigger file
sizes, the performance advantage of using faster hash
function can go up to a factor of 5 or 6 (Edon-R512
vs SHA-256).
10
100
1000
10000
0 16K 32K 64K 128K 256K 512K 1M 4M 10M
BMW512
22656 12534 8753 5448 3055 1623 841 428 107 42
Edon R512
22018 14092 10527 6831 4036 2176 1140 585 142 57
SHA256
21516 5157 2942 1580 820 418 211 105 26 11
SHA512
22515 7026 4221 2337 1231 633 321 160 40 16
Shabal512
21834 9290 6205 3617 1945 1015 519 262 66 26
Skein512
22418 10004 6519 3821 2101 1097 562 280 70 28
Num be r o f ver if i ed fi le s p er se c on d
Verification with RSA1536 combined with different hash functions
10
100
1000
10000
0 16K 32K 64K 128K 256K 512K 1M 4M 10M
BMW512
22656 12534 8753 5448 3055 1623 841 428 107 42
Edon R512
22018 14092 10527 6831 4036 2176 1140 585 142 57
SHA256
21516 5157 2942 1580 820 418 211 105 26 11
SHA512
22515 7026 4221 2337 1231 633 321 160 40 16
Shabal512
21834 9290 6205 3617 1945 1015 519 262 66 26
Skein512
22418 10004 6519 3821 2101 1097 562 280 70 28
Num be r o f ver if i ed fi le s p er se c on d
Verification with RSA1536 combined with different hash functions
Figure 7: Verification speed of RSA1536 with different
hash functions and different file sizes. The numbers are
expressed in number of verifications in one second on the
referent machine (Intel i7 CPU on 2GHz).
Verification with ECDSA192 combined with different hash functions
d
1000
nsec or pes fil ed
100
fieri v e oferm bNu
10
0 16K 32K 64K 128K 256K 512K 1M 4M 10M
BMW512
1229 1184 1120 1041 901 716 516 320 98 41
Edon R512
1222 1203 1148 1095 997 836 642 423 139 61
SHA256
1205 1015 890 684 487 303 174 93 25 10
SHA512
1221 1104 988 829 629 423 257 142 39 16
Shabal512
1213 1163 1063 970 783 574 373 219 62 26
Skein512
1204 1126 1060 924 749 540 348 199 57 23
10
100
1000
0 16K 32K 64K 128K 256K 512K 1M 4M 10M
BMW512
1229 1184 1120 1041 901 716 516 320 98 41
Edon R512
1222 1203 1148 1095 997 836 642 423 139 61
SHA256
1205 1015 890 684 487 303 174 93 25 10
SHA512
1221 1104 988 829 629 423 257 142 39 16
Shabal512
1213 1163 1063 970 783 574 373 219 62 26
Skein512
1204 1126 1060 924 749 540 348 199 57 23
Num be r o f ver ifi ed fi le s p er sec on d
Verification with ECDSA192 combined with different hash functions
Figure 8: Verification speed of ECDSA192 with different
hash functions and different file sizes. The numbers are
expressed in number of verifications in one second on the
referent machine (Intel i7 CPU on 2GHz).
As a conclusion from this part we can say that the
industrial demand for very fast hash functions in soft-
ware will increase in the forthcoming period. The
speed of execution of those hash functions should
preferably be in the range beneath 2 cycles per byte.
5 ON RECENT CPUS FROM
INTEL, AMD AND IBM
In the last few years the server infrastructure of our
society has been remarkably fast 64bit-ized.
INTERNATIONALLY STANDARDIZED EFFICIENT CRYPTOGRAPHIC HASH FUNCTION
431

The development in the robust 64-bit CPUs is
mainly carried by three big companies: Intel, AMD
and IBM.
We can argue that the current line of the most re-
cent CPU architectures: Sandy Bridge of Intel, Bull-
dozer of AMD and Power7 of IBM, offer huge com-
putational potentials from a hash design point of view.
All three architectures offer SIMD operations with
32-bit or 64-bit values over 128-bit or 256-bit regis-
ters, out-of-order execution, executions of several in-
structions per cycle, multiple integer execution units
per core and very fast read and write to the L1 cache
where the speed is more than 16, 24 or 32 bytes per
cycle.
However, from an engineering point of view, we
have a position that neither SHA-2 nor any of the
SHA-3 finalists exploit this huge potential of concur-
rency in recent 64-bit CPUs.
On the embedded side, driven by application seg-
ments like smartphones, there has been a drive to-
wards 32-bit architectures. What is interesting is that
there is an architecture convergence, where the fea-
tures of server side CPU’s like advanced SIMD units
as NEON in the recent ARM architectures are creep-
ing into embedded devices. This allows us to extend
our arguments about development for modern archi-
tecture well into the embedded area.
As a conclusion we can say that engineering de-
velopments in the recent CPUs are offering techno-
logical pre-conditions to meet our deepened theoret-
ical understanding of what should be included in the
design of secure hash functions, which will indeed be
significantly more efficient than SHA-2 i.e. to be more
precise: in software to be at least 3 times faster than
SHA-2.
6 CRITERIA FOR AN
INTERNATIONALLY
STANDARDIZED EFFICIENT
CRYPTOGRAPHIC HASH
FUNCTION
The previous European standard RIPEMD-160 did
not become widely used by the industry due to its
inferior performance compared to SHA-1 and MD5.
Taking into consideration all arguments that we have
given so far in this positional paper:
1. The industrial needs of the modern standards for very
fast hash functions;
2. The rapid development of the computational power of
recent CPUs;
3. SHA-3 will not be significantly faster than SHA-2;
we claim that European research and development
community can initiate a design of secure crypto-
graphic hash function that will be widely accepted
by the industry due to its superior performances com-
pared to any of MD5, SHA-1, SHA-2 or SHA-3.
Such an initiative can be organized as a world-
wide open effort or competition, run by ISO/IEC JTC
1/SC 27, or by the European standardization organi-
zations CEN, CENELEC and ETSI as they have been
already mandated by the European Commission (EC)
for adoption of different standards in the information
security.
The criteria for that standard from a security and
efficiency point of view should be similar to the secu-
rity criteria for SHA-3, but in some parts clarified, i.e.
without the fuzziness that was present in some of the
SHA-3 criteria (like the fuzziness about the efficiency
or about the resistance against the length-extensionat-
tack). We give here an initial proposal for those crite-
ria:
1. Security
(a) Preimage resistance of 224, 256, 384 and 512 bits.
(b) Second Preimage resistance (for short messages) of
224, 256, 384 and 512 bits.
(c) Collision resistance of 112, 128, 192 and 256 bits.
(d) Length extension attack resistance of 224, 256, 384
and 512 bits.
2. Speed in software in 64-bit mode: Faster than 2 cycles
per byte.
3. Speed in software in 32-bit mode (for embedded appli-
cations): Faster than 3 cycles per byte.
7 FACTS AND CLAIMS INSTEAD
OF A CONCLUSION
Here is a collection of facts that were presented in
different sections of this positional paper:
1. There is a clear industrial need for very efficient
and secure cryptographic hash function.
2. The speed of the MD5 hash function is still un-
surpassed by any standardized hash function, and
that is the main reason MD5 is still being used de-
spite the fact that it is practically broken.
3. The situation with SHA-1 is similar to that of
MD5. It is widely used, despite the fact that it
is theoretically broken.
4. The current cryptographic hash standard SHA-2
is 2 to 8 times slower than MD5 and SHA-1.
5. The upcoming SHA-3 standard will be slower
than MD5 and SHA-1, and will not be signifi-
cantly faster than SHA-2.
SECRYPT 2011 - International Conference on Security and Cryptography
432

6. The SHA-3 competition has stimulated the re-
search and deepened the scientific understanding
about the design principles of secure hash func-
tions.
7. The current and anticipated technological devel-
opments in the design of recent CPUs open pos-
sibilities for cryptographers to design secure and
significantly more efficient hash functions.
8. An internationally standardized efficient crypto-
graphic hash function does not necessarily need
to be SHA-2, SHA-3 (or SHA-4).
9. An internationally standardized efficient crypto-
graphic hash function can be significantly more
efficient than MD5, SHA-1, SHA-2 and SHA-3.
REFERENCES
ANSI (1998). ANSI X9.31-1998 Digital Signatures Using
Reversible Public Key Cryptography for the Financial
Services Industry (rDSA). American National Stan-
dards Institute. http://csrc.nist.gov/groups/ST/hash/
index.html.
Bernstein, D. J. and Lange, T. (2011). SUPERCOP: Ecrypt
benchmarking of cryptographic systems.
Bosselaers, A., Dogbbertin, H., and Preneel, B. (1997). The
RIPEMD-160 cryptographic hash function. 22(1):24,
26, 28, 78, 80.
Bresson, E., Canteaut, A., Chevallier-Mames, B., Clavier,
C., Fuhr, T., Gouget, A., Icart, T., Misarsky, J.-F., M,
Naya-Plasencia, Paillier, P., Pornin, T., Reinhard, J.-
R., Thuillet, C., and Videau, M. (2008). Shabal. In
Submission to NIST.
Diffie, W. and Hellmann, M. (1976). New directions in
cryptography. In IEEE Trans. on Info. Theory, vol-
ume IT-22, pages 644–654.
Dobbertin, H., Bosselaers, A., and Preneel, B. (1996).
Ripemd-160: A strengthened version of ripemd. In
Gollmann, D., editor, FSE, volume 1039 of Lecture
Notes in Computer Science, pages 71–82. Springer.
Ferguson, N., Lucks, S., Schneier, B., Whiting, D., Bellare,
M., Kohno, T., Callas, J., and Walker, J. (2009). The
skein hash function family. In Submission to NIST
(Round 2).
Fleischmann, E., Forler, C., and Gorski, M. (2008). Clas-
sification of the sha-3 candidates. Cryptology ePrint
Archive, Report 2008/511. http://eprint.iacr.org/.
Gligoroski, D., Klima, V., Knapskog, S. J., El-Hadedy, M.,
Amundsen, J., Mjølsnes, S. F., Jensen, R. E., and Otte,
D. (2009). Cryptographic hash function BLUE MID-
NIGHT WISH. In Submission to NIST (Round 2).
Gligoroski, D., Ødeg˚ard, R. S., Mihova, M., Knapskog,
S. J., Kocarev, L., Dr´apal, A., and Klima, V. (2008).
Cryptographic hash function EDON-R. In Submission
to NIST.
IEEE-SA-Standards-Board (2000). IEEE Std 1363-2000,
IEEE Standard Specifications for Public-Key Cryp-
tography. IEEE Computer Society.
ISO/IEC (2006). ISO/IEC 14888 - Digital signatures with
appendix. ISO/IEC.
Kaliski, B. (April 1992). The md2 message-digest algo-
rithm. In RFC 1319. Network Working Group, RSA
Laboratories.
Levin, L. A. (1987). One-way functions and pseudorandom
generators. In Combinatorica, volume 7, pages 357–
363.
Menasce’, D. A. (2003). Security performance. IEEE In-
ternet Computing, 7(3):84–87.
NEMA (2001). Digital Imaging and Communications in
Medicine (DICOM) - Digital Signatures. National
Electrical Manufacturers Association. ftp:// medi-
cal.nema.org/medical/dicom/final/sup41 ft.pdf.
NIST (1992). Publication YY: Announcement and Specifi-
cations for a Secure Hash Standard (SHS).
NIST (2002). Secure Hash Standard. National Institute
of Standards and Technology, Washington. Federal
Information Processing Standard 180-2.
NIST (2009). Digital Signature Standard (DSS). Federal
Information Processing Standard 186-3.
Preneel, B. (2010). Cryptographic hash functions and the
nist sha-3 competition.
Rivest, R. (April 1992). The md5 message-digest algorithm.
In RFC 1321. Network Working Group, MIT Labo-
ratory for Computer Science and RSA Data Security
Inc.
Rivest, R. (October 1990). The md4 message-digest algo-
rithm. In RFC 1186. Network Working Group, MIT
Laboratory for Computer Science and RSA Data Se-
curity Inc.
Yao, A. (1982). Theory and application of trapdoor func-
tions. In Proceedings of 23rd IEEE Symposium on
Foundations of Computer Science, pages 80–91.
Zheng, Y., Pieprzyk, J., and Seberry, J. (1992). Haval
- a one-way hashing algorithm with variable length
of output. In Seberry, J. and Zheng, Y., editors,
AUSCRYPT, volume 718 of Lecture Notes in Com-
puter Science, pages 83–104. Springer.
INTERNATIONALLY STANDARDIZED EFFICIENT CRYPTOGRAPHIC HASH FUNCTION
433
