TOWARDS HIGHER-ORDER MUTANT GENERATION

FOR WS-BPEL

E. Blanco-Mu˜noz, A. Garc´ıa-Dom´ınguez, J. J. Dom´ınguez-Jim´enez and I. Medina-Bulo

University of C´adiz, C/ Chile, 1, C´adiz, Spain

Keywords:

Mutation testing, Genetic algorithm, Web services, Web service compositions, WS-BPEL.

Abstract:

We present an architecture for automatically generating higher-order mutants for WS-BPEL compositions

based on the architecture of GAmera, a ﬁrst-order mutant generation system for WS-BPEL. Higher-order

mutants are created by applying a sequence of ﬁrst-order mutation operators to the original program. This

paper also introduces the changes that GAmera has to undergo for converting the generation of ﬁrst-order

mutants into a process capable of higher-order mutation, while detailing the modiﬁcations carried out for

adapting the crossover and mutation genetic operators to the new structure of the mutants.

1 INTRODUCTION

The Web Services Business Process Execution Lan-

guage (WS-BPEL) (OASIS, 2007) allows us to de-

velop new Web Services (WS) modelling more com-

plex business processes on top of preexisting WS. The

economic impact of WS-BPEL service compositions

is quickly increasing (IDC, 2008), and deeper insight

on how to test them effectively is therefore required.

Mutation testing (DeMillo et al., 1978; Ham-

let, 1977) is a testing technique that has been ap-

plied successfully to several programming languages.

Several mutant generation systems already exist (Jia

and Harman, 2010), such as Mothra (King and Of-

futt, 1991) for FORTRAN, MuJava (Ma et al., 2005)

for Java, SQLMutation (Tuya et al., 2007) for SQL,

among others. In fact, we have presented GAm-

era (Dom´ınguez-Jim´enez et al., 2009) in previous

works, an automatic mutant generation system for

WS-BPEL compositions, which only deals with ﬁrst-

order mutants. GAmera is the ﬁrst mutant generator

based on a genetic algorithm (GA) (Goldberg, 1989).

However, all these tools only generate ﬁrst-order

mutants. In this work we present the modiﬁcations

of the architecture of GAmera for automatically gen-

erating higher-order mutants for WS-BPEL composi-

tions. A higher-order mutant is created by applying a

sequence of ﬁrst-order mutation operators to the orig-

inal program (Jia and Harman, 2009). It has been

shown empirically that about 99% of higher-order

mutants are distinguished by test data that distinguish

ﬁrst-order mutants (known as the coupling effect)

(Mathur, 1994; Wah, 2003).

This paper introduces the changes GAmera re-

quires to convert the generation of ﬁrst-order mutants

into a process capable of higher-order mutation, while

detailing the modiﬁcations carried out for adapting

the crossover and mutation genetic operators to the

new structure of the mutants.

The paper is divided into the following sections:

Section 2 brieﬂy summarizes the WS-BPEL lan-

guage, mutation testing and genetic algorithms. Sec-

tion 3 describes the modiﬁcations to the architecture

of GAmera, as well as the new genetic operators de-

ﬁned. Finally, Section 5 presents the conclusions and

future work.

2 BACKGROUND

We will ﬁrst introduce the WS-BPEL language and

mutation testing, and then offer some basic concepts

about genetic algorithms.

2.1 The WS-BPEL Language

WS-BPEL (Organization for the Advancement of

Structured Information Standards, 2007) is an XML-

based language which implements a business process

as a WS which interacts with other external WS. Stan-

dard WS-BPEL process deﬁnitions are not coupled to

the implementation details of the WS-BPEL engine

143

Blanco-Muñoz E., García-Domínguez A., J. Domínguez-Jiménez J. and Medina-Bulo I..

TOWARDS HIGHER-ORDER MUTANT GENERATION FOR WS-BPEL.

DOI: 10.5220/0003611901430148

In Proceedings of the International Conference on e-Business (ICE-B-2011), pages 143-148

ISBN: 978-989-8425-70-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

they run on or the WS they invoke. WS-BPEL pro-

cess deﬁnitions can be divided in four sections:

1. Declarations of the relationships to the external

partners. These include both the client that has in-

voked the business process and the external part-

ners whose services are required to complete the

request of the client.

2. Declarations of the variables used by the process

and their types. Variables are used for storing both

the messages received and sent from the business

process and the intermediate results required by

the internal logic of the composition.

3. Declarations of handlers for various situations,

such as fault, compensation or event handlers.

4. Description of the business process behavior.

The major building blocks of a WS-BPEL process

are activities, XML elements which model assign-

ments, control structures, message passing primitives

or synchronization constraints, among others. There

are two types: basic and structured activities. Basic

activities specify a single action, such as receiving a

message from a partner or performing an assignment

to a variable. Structured activities contain other ac-

tivities and prescribe their execution order. Activi-

ties may have both attributes and a set of containers.

These containers can also include elements with their

own attributes. Here is an example:

<flow>

← Structured activity

<links>

← Container

← Element

</links>

<invoke name="checkFlight"

.. .

← Basic activity

← Container

← Element

</sources>

</invoke>

<invoke name="checkHotel"

.. .

<invoke name="checkRentCar"

.. .

<invoke name="bookFlight"

← Attribute . ..

← Container

</targets>

</invoke>

</flow>

WS-BPEL provides concurrency and synchro-

nization primitives. For instance, the

flow

activ-

ity runs a set of activities in parallel. Synchroniza-

tion constraints between activities can be deﬁned. In

the above example, the

flow

activity invokes three

WS in parallel:

checkFlight

checkHotel

, and

checkRentCar

. There is another WS,

bookFlight

that will only be invoked if

checkFlight

is com-

pleted. Activities are synchronized by linking them:

the target activity of every link will only be executed

if the source activity of the link has been completed

successfully.

2.2 Mutation Testing

Mutation testing (DeMillo et al., 1978; Hamlet, 1977)

is a fault-based testing technique that introduces sim-

ple ﬂaws in the original program by applying muta-

tion operators. The resulting programs are called mu-

tants. Each mutation operator models a category of

errors that the developer could make. For instance,

if a program contains the instruction

a > 5000

and

we apply the relational mutation operator (which re-

places a relational operator with another), one of the

mutants produced will contain

a < 5000

instead. If

a test case can tell apart the original program and the

mutant, i.e. their outputs are shown to be different, it

is said that this test case kills the mutant. Otherwise,

the mutant is said to stay alive.

Equivalent mutants, which always produce the

same output as the original program, are a common

problem when applying mutation testing. Equivalent

mutants should not be confused with stubborn non-

equivalent mutants, which are produced because the

test suite is not adequate to detect them. The general

problem of determiningif a mutant is equivalentto the

original program is undecidable (Zhu et al., 1997).

2.3 Genetic Algorithms

Genetic Algorithms (Goldberg, 1989; Holland, J. H.,

1992) are probabilistic search techniques based on the

theory of evolution and natural selection.

GAs work with a population of solutions, known

as individuals, and process them in parallel. Through-

out the successive generations of the population, GAs

perform a selection process to improve the popula-

tion, and so they are ideal for optimization. In this

sense, GAs favor the best individuals and generate

new ones through the recombination and mutation

of information from existing ones. The strengths of

GAs are their ﬂexibility, simplicity and ability for hy-

bridization. Among their weaknesses are their heuris-

tic nature and their difﬁculties in handling restrictions.

The ﬁtness of an individual measures its quality as

a solution for the problem to be solved. The average

ﬁtness of the population will be maximized along the

generations produced by the GA.

GAs use two types of genetic operators: selection

and reproduction. Selection operators select individ-

uals in a population for reproduction. The likelihood

of selecting an individual may be proportional to its

ﬁtness. Reproduction operators generate the new in-

dividuals in the population by applying crossover and

mutation operators. On the one hand, crossover op-

erators generate two individuals (children) from two

pre-selected individuals (parents). The children in-

ICE-B 2011 - International Conference on e-Business

144

herit part of the information stored in both parents.

On the other hand, mutation operators aim to alter

the information stored in an individual. The design

of these operators heavily depends on the encoding

scheme used. It is important to note that these muta-

tion operators are related to the GA and are different

from those for mutation testing.

3 SYSTEM ARCHITECTURE

This section describes how GAmera has changed

from its previous architecture, the new genetic oper-

ators which have been adapted to the current frame-

work and lastly, the novel genetic algorithm. The

components of GAmera are still the same, although

the genetic search for mutants has been modiﬁed. Fig-

ure 1 shows the core of the system: the analyzer, the

mutant generator and the execution system. The an-

alyzer takes the original program WS-BPEL process

deﬁnition and produces the information required by

the mutant generator. The mutant generator is divided

into the GA and a converter from the individuals of

the GA to the mutants of the original process deﬁni-

tion. Finally, the execution system runs the generated

mutants against the test cases and compares their out-

puts with those from the original process deﬁnition.

Genetic algorithm Converter

Analyzer

Execution engine

Mutant WS−BPEL 2.0 program

Original WS−BPEL 2.0 program Mutation operator analysis

MUTANT GENERATOR

mutantsmutantsequivalent

mutants

suite

Potentially

Test

Killed Stillborn

Figure 1: GAmera architecture.

3.1 Higher-order Structure

Figure 2 shows the new structure for generating

higher-order mutants (HOM).

3.1.1 Extending the Representation

The concept of individual has been changed. Individ-

uals now encode N mutations on the original program,

where N is the maximum order deﬁned in the conﬁg-

uration. Individuals have ﬁve ﬁelds (Figure 3): the

order of the individual, its ﬁtness, the identiﬁers of

the mutation operators to be applied, the identiﬁers of

the locations to be mutated and the additional values

which modify the behaviour of the selected mutation

operator. The three lists with the mutation operators,

the locations and the additional values must have the

same number of elements.

With the new structure, we now deﬁne two indi-

viduals to be equal if they have the same order (n)

and the ﬁrst n operator-location-attribute triplets are

equal. Populations contain sequences of individuals:

some of them may be equal to others.

In addition to regular populations for each gener-

ation, we keep a separate population during the exe-

cution of the GA, called the Hall of Fame (HOF). The

HOF collects the individuals generated by the GA in

previous generations. Each distinct individual is only

stored once, unlike in regular populations. Individuals

in the HOF also contain their Execution Rows with the

results produced when the mutant was executed. We

will detail this further in the next section.

3.1.2 Fitness of the Individuals

Once the analyzer has ﬁnished, we know which muta-

tion operators can be applied. If the value of the ﬁeld

Location is zero, it means that mutation operator can-

not be used by the genetic algorithm. Therefore, it is

necessary to ﬁlter the usable combinations.

To calculate the ﬁtness of the individuals we have

to convert them into mutants, by applying each mu-

tation operator in sequence. After applying the last

mutation operator mentioned in the individual, the re-

sulting HOM can be run with the execution system.

The execution row of each individual is produced

by running the corresponding mutant against all test

cases. For each test case in the suite, its column re-

ports if the mutant stayed alive (0), if it was killed (1)

or if it could not be deployed (2).

Having set this ﬁeld in the individuals of the HOF,

the individual ﬁtness of the current population can

now be calculated. We use the original ﬁtness func-

tion of GAmera. The ﬁtness for individual I is given

by:

Fitness(I) = M · T −

∑

j=1

I j

∑

i=1

(1)

where M is the number of mutants in a generation,

T represents the cases number of the test suite and m

shows the execution row of an individual I.

3.1.3 New Genetic Operators

The ﬁrst population is randomly generated. The fol-

lowing generations are based on a generational GA

where individuals come from:

• Random generation. There is a percentage in the

conﬁguration to know how many mutants will be

randomly generated.

TOWARDS HIGHER-ORDER MUTANT GENERATION FOR WS-BPEL

145

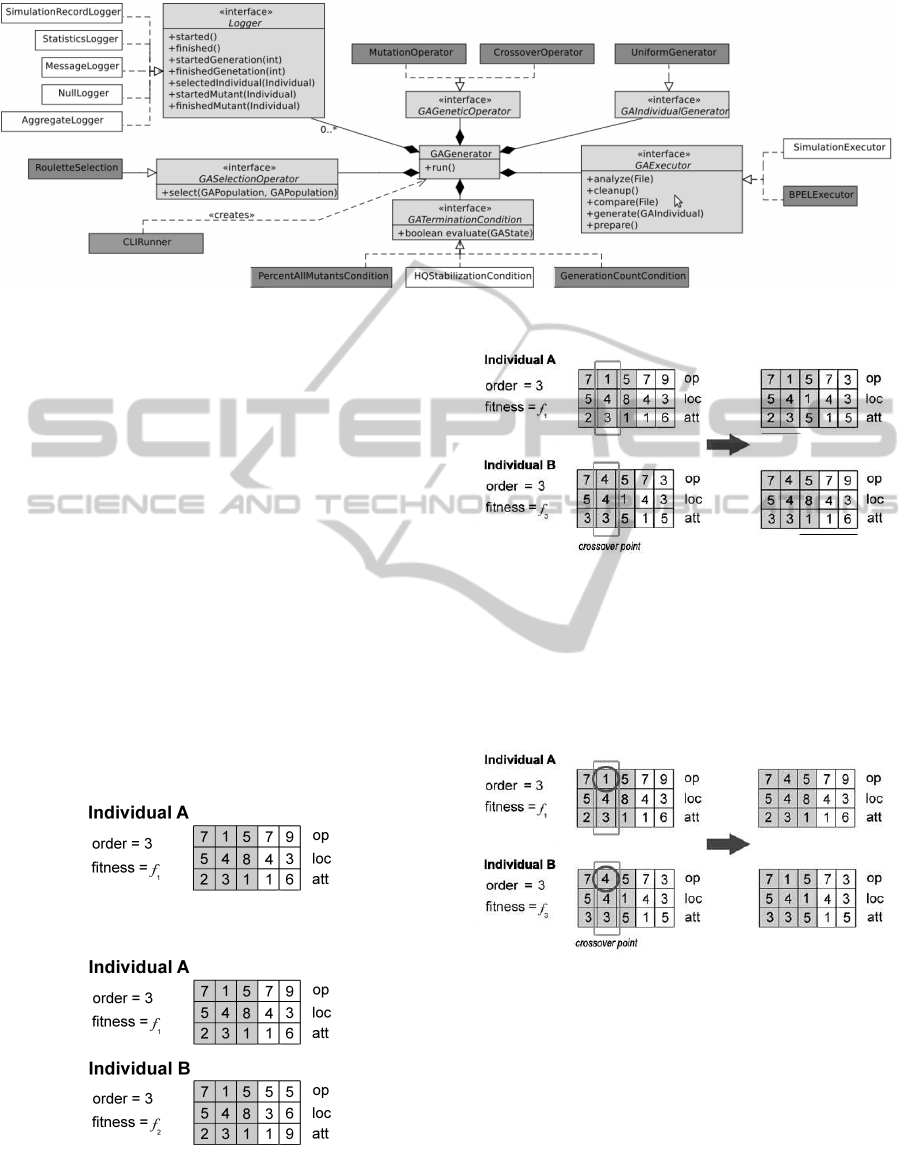
Figure 2: New higher-order structure.

• Crossover and mutation operations. The selection

of individuals involved in the operations is done

through the roulette wheel method. Crossovers

and mutations will be done according to the prob-

abilities speciﬁed in the conﬁguration, p

and

= 1 − p

, respectively. These operations have

undergone several changes that are detailed be-

low.

The crossover operator consists in an exchange of

certain ﬁelds of the individuals involved. There are

two types of crossover operators: the order and the

individual crossover operator. Their probabilities are

set in the conﬁguration: p

and p

, respectively, so

= p

+ p

In the order crossover operator, a crossover point

is chosen at random, between 1 to the order of the

individual. Figure 5 shows how two parents gener-

ate their children, according to the selected crossover

point.

Figure 3: Representation of an individual.

Figure 4: Equal individuals.

On the other hand, in the individual crossover op-

erator, a crossover point is also chosen in the same

Figure 5: Order crossover operator.

way, but now the ﬁeld which will be changed (opera-

tor, location or attribute) is randomly selected. There-

fore, in this case only a value of each individual is

modiﬁed. Figure 6 has an example of applying an in-

dividual crossover operator.

Figure 6: Individual crossover operator.

The mutation operator changes the value of a ﬁeld

of the individual. There are two types of mutation op-

erators: the order and the individual mutation opera-

tor. Their probabilities are set by the user: p

and

, respectively, so p

= p

+ p

In the order mutation operator, the parameter

which will be modiﬁed is the individual order and it

will be given by:

Order(I) = o

current

+ rand(−1, 1) · (1− p

) (2)

ICE-B 2011 - International Conference on e-Business

146

Figure 7: Order mutation operator.

In the individual mutation operator, a mutation

point is randomly chosen and the ﬁeld which will

be mutated (operator, location or attribute) is selected

randomly. The value which will be changed is given

by:

Value(I) = v

current

+ rand(−1, 1) · (1− p

) (3)

Figure 8: Individual mutation operator.

The GA will stop when the maximum percentage

of generated mutants is reached.

4 RELATED WORKS

There are many papers on the application of mutation

testing (Jia and Harman, 2010). Research in muta-

tion testing can be classiﬁed into four types of activi-

ties (Offutt et al., 2006):

1. Deﬁning mutation operators.

2. Developing mutation systems.

3. Inventing ways to reduce the cost of mutation

analysis.

4. Experimentation with mutation.

This paper focuses on the second activity. Several

mutant generation systems for various programming

languages already exist:

• Mothra (King and Offutt, 1991) for FORTRAN. It

is likely the most widely known mutation testing

system.

• MuJava (Ma et al., 2005) for Java.

• Proteum (Delamaro and Maldonado, 1996) for C.

It implements all mutation operators designed for

the ANSI C programming language.

• MILU (Jia and Harman, 2008) for C. It can per-

form both ﬁrst-order and higher-order mutation

testing.

• SQLMutation (Tuya et al., 2007) for database

queries written in SQL.

• GAmera (Dom´ınguez-Jim´enez et al., 2009) for

WS-BPEL. This generator is the ﬁrst mutant gen-

eration system based on GA.

We present a new mutant generation system based

on GAmera. This mutant generation system operates

over WS-BPEL process deﬁnitions, and it incorpo-

rates the generation of higher-order mutants.

5 CONCLUSIONS AND FUTURE

WORK

This paper presents an approach towards implement-

ing an automatic higher-order mutant generation sys-

tem for WS-BPEL compositions. It improves upon

our previous tool, called GAmera, which only deals

with ﬁrst-order mutants.

We have also described the changes needed to

adapt the crossover and mutation operators to the new

structure of the mutants. An advantage of this new

approach is that mutants from different orders can be

mixed in the same generation.

The most important contribution of this work is

the proposal of the design of the ﬁrst framework

which generates higher-order mutants for WS-BPEL

compositions.

Our future lines of work are the implementation

of this framework in Java. This includes the new ar-

chitecture presented in Figure 2, the extension of indi-

vidual representation, and new genetic operators pre-

sented in Section 3.1.3. Finally, we will design an

user-friendly graphical interface.

REFERENCES

Delamaro, M. and Maldonado, J. (1996). Proteum–a tool

for the assessment of test adequacy for C programs.

In Proceedings of the Conference on Performability in

Computing System (PCS 96), pages 79–95.

DeMillo, R. A., Lipton, R. J., and Sayward, F. G. (1978).

Hints on test data selection: Help for the practicing

programmer. Computer, 11(4):34–41.

Dom´ınguez-Jim´enez, J. J., Estero-Botaro, A., Garc´ıa-

Dom´ınguez, A., and Medina-Bulo, I. (2009).

GAmera: an automatic mutant generation system for

WS-BPEL compositions. In ECOWS’09: Proceed-

ings of the Seventh IEEE European Conference on

Web Services.

Goldberg, D. E. (1989). Genetic algorithms in search, op-

timization and machine learning. Addison-Wesley,

Reading.

Hamlet, R. G. (1977). Testing programs with the aid of a

compiler. IEEE Transactions Software Engineering,

3(4):279–290.

TOWARDS HIGHER-ORDER MUTANT GENERATION FOR WS-BPEL

147

Holland, J. H. (1992). Adaptation in natural and artiﬁcial

systems. MIT Press, Cambridge.

IDC (2008). Research reports. http://www.idc.com.

Jia, Y. and Harman, M. (2008). MILU: A customizable,

runtime-optimized higher order mutation testing tool

for the full C language. In TAIC-PART ’08: Proceed-

ings of the Testing: Academic & Industrial Confer-

ence - Practice and Research Techniques, pages 94–

98. IEEE Computer Society.

Jia, Y. and Harman, M. (2009). Higher order muta-

tion testing. Information and Software Technology,

51(10):1379–1393.

Jia, Y. and Harman, M. (2010). An analysis and survey of

the development of mutation testing. IEEE Transac-

tions on Software Engineering, 99(PrePrints).

King, K. N. and Offutt, A. J. (1991). A FORTRAN

language system for mutation-based software testing.

Software - Practice and Experience, 21(7):685–718.

Ma, Y.-S., Offutt, J., and Kwon, Y. R. (2005). MuJava: an

automated class mutation system. Software Testing,

Veriﬁcation & Reliability, 15(2):97–133.

Mathur, A. (1994). Mutation testing. In Marciniak, J. J.,

editor, Encyclopedia of Software Engineering, pages

707–713. Wiley, New York, NY.

OASIS (2007). Web Services Business Process

Execution Language 2.0. http://docs.oasis-

open.org/wsbpel/2.0/OS/wsbpel-v2.0-OS.html.

Organization for the Advancement of Structured

Information Standards.

Offutt, J., Ma, Y.-S., and Kwon, Y.-R. (2006). The class-

level mutants of MuJava. In AST ’06: Proceedings

of the 2006 international workshop on Automation

of software test, pages 78–84, New York, NY, USA.

ACM.

Organization for the Advancement of Structured Informa-

tion Standards (2007). Web Services Business Process

Execution Language 2.0. (Last accessed: 2 March

2011).

Tuya, J., Cabal, M. J. S., and de la Riva, C. (2007). Mutating

database queries. Information and Software Technol-

ogy, 49(4):398–417.

Wah, K. S. H. T. (2003). An analysis of the coupling effect

i: single test data. Science of Computer Programming,

48(2–3):119–161.

Zhu, H., Hall, P., and May, J. (1997). Software unit test

coverage and adequacy. ACM Computing Surveys,

29(4):366–427.

ICE-B 2011 - International Conference on e-Business

148