FUZZY APPROACHES FOR MODELING DYNAMICAL

ECOLOGICAL SYSTEMS

Àngela Nebot

, Francisco Mugica

, Benjamín Martínez-López

and Carlos Gay

Soft Computing Group, Universitat Politècnica de Catalunya, Jordi Girona Salgado 1-3, Barcelona, Spain

Centro de Ciencias de la Atmósfera, Universidad Nacional Autónoma de México, Circuito Exterior s/n

Ciudad Universitaria, Del. Coyoacán, 04510, Mexico

Keywords: Fuzzy logic, Soft computing, Global temperature change, Neuro-fuzzy systems, Genetic-fuzzy systems,

FIR.

Abstract: This research shows the usefulness of fuzzy logic approaches for modelling and simulation of complex

dynamical systems. Several hybrid soft computing methodologies based on fuzzy logic, such are neuro-

fuzzy systems, genetic-fuzzy systems and the Fuzzy Inductive Reasoning are applied to a real dynamical

system in the ecological domain, i.e. the global temperature change. The ocean-atmosphere system is

represented in this work by using an energy balance model that reproduces a range of temperatures increase

that agrees with that reported by the IPCC. The results obtained by all the fuzzy approaches studied are

good, although the Fuzzy Inductive Reasoning methodology performs clearly much better that the other

approaches for the application studied from the prediction accuracy point of view.

1 INTRODUCTION

The global climate is a highly complex system in

which take place many physical, chemical, and

biological processes, in a wide range of space and

time scales. These processes are simulated by global

circulation models, which are computer models

based on the fundamental laws of physics and they

are the principal tool for predicting the response of

the climate to increases in greenhouse gases. With

the increase of computational resources, complex

global models are frequently being used to assess the

response of the climate system to the projected

increase in the amount of greenhouse gases. All

model experiments point to global warming through

the coming centuries. These models, however, are

not perfect representations of reality because, among

other reasons, they do not include important physical

processes (e.g. ocean eddies, gravity waves,

atmospheric convection, clouds and small-scale

turbulence) that are known to be key aspects of the

climate system but that are too small or fast to be

explicitly modelled (Williams, 2005). In addition,

the high complexity of the climate system

represents, by itself, a crucial constraint in the

prediction of future climate change. Therefore, even

the most complex climate models are unable to

project how climate will change with certainty, as it

is reflected in the wide range of temperature increase

reported by the IPCC 4AR (IPCC, 2007).

Simple models of the climate system have been

developed and used to gain physical insight into

major features of the behaviour of the climate

system. These simple models have also been

frequently used to conduct sensitivity studies and to

produce climate projections for a range of

assumptions about emissions of carbon dioxide and

other greenhouse gases.

Fuzzy logic is a very powerful approach for

managing uncertainties inherent to complex systems.

Fuzzy systems have demonstrated their ability to

solve different kind of problems like control (e.g.

Watanabe et al., 2005) and have been successfully

applied to a wide range of applications, i.e. signal

and image processing (Bloch, 2005) and medical

applications (Nebot et al., 2003), etc. To the authors’

knowledge, there are very few studies that apply

fuzzy logic approaches to study the global

temperature change problem.

In the next section, we use a simple box model of

the ocean-atmosphere to assess the response of the

global mean temperature to changes in the thermal

forcing and to model parameters. This model

depends on a small number of parameters which are

374

Nebot À., Mugica F., Martínez-López B. and Gay C..

FUZZY APPROACHES FOR MODELING DYNAMICAL ECOLOGICAL SYSTEMS.

DOI: 10.5220/0003614603740379

In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2011), pages

374-379

ISBN: 978-989-8425-78-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

treated directly as fuzzy logic sets. Section 3

describes shortly the hybrid fuzzy methods studied

and presents the results. Section 4 presents a

comparison table of the different methodologies

performances and discusses the results. Finally the

conclusions of this work are given.

2 GLOBAL TEMPERATURE

CHANGE EXPERIMENT

In this section, we use a box model of the ocean-

atmosphere to determine whether this simple model

is able to reproduce the wide range of temperature

increase reported by the IPCC, when plausible

model parameters and surface forcing are used.

The ocean-atmosphere system is represented by

using a simple energy balance model consisting of

two boxes that represent the atmosphere (one over

the land and the other over the ocean) and two boxes

that represent the oceanic mixed layer coupled to a

diffusive ocean (Fig. 1).

The analytical solution of this kind of model can

be found in Wigley and Schlesinger (1985). The

brief description given here follows closely that of

McGuffie and Henderson-Sellers (2005). The

heating rate of the mixed layer is calculated by

assuming a constant depth in which the temperature

difference (ΔT), associated with some perturbation,

changes in response to: changes in the surface

thermal forcing (ΔQ); the atmospheric feedback,

which is expressed in terms of a climate feedback

parameter (λ); leakage of energy from the mixed

layer to the deeper ocean (ΔM). This energy flux is

used as an upper boundary condition for the

diffusive deep ocean in which the thermal diffusion

coefficient (K) is assumed to be a constant.

The

equations describing the rates of heating in

the two layers are: for the mixed layer, with total

heat capacity Cm,

MTQ







(1)

for the deeper ocean layer,











(2)

At the interface between the surface and the deeper

layers, there is an energy source which acts as a

surface boundary condition (2). A simple

parameterization is used by imposing continuity

between the mixed-layer temperature change (ΔT)

and the deeper-layer temperature change evaluated

at the interface,

),0(

tzT 

, i.e.

)(),0(

tTtT





Figure 1: Ocean-atmosphere system using a simple energy

balance model.

With this formulation, ΔM can be calculated from





















KcM



(3)

and used in (1). In the last equation, γ is the

parameter utilized to average over land and ocean

(values between 0.72 and 0.75), ρ

is the water

density and c

is its specific heat capacity.

Equations (1) and (2) are integrated numerically

for a period of 100 years using a forward Euler

scheme and a vertical grid for the deep ocean. All

model experiments are performed using a time step

of one day and a vertical grid with 100 points and a

spacing of 5 m, which represents a deep ocean layer

of 500 m. The internal model parameters and the

change in thermal forcing vary as follows: λ varies

from 0 to 4 Wm

-2

-1

, with increments of 0.25; K

varies from 10

-4

to 10

-5

-1

, with increments

105.0





; ΔQ varies from 0 to 8 Wm

-2

, with

increments of 0.5. A total of 6069 integrations (each

one corresponding to a combination of the varying

internal model parameters and the thermal forcing)

are carried out over the 100-year period. This range

of temperatures increase agrees with that reported by

the IPCC (IPCC, 2007).

3 FUZZY MODELING

APPROACHES

As Klir stated in his book (Klir and Elias, 2002), the

view of the concept of uncertainty has been changed

in science over the years. The traditional view looks

to uncertainty as undesirable in science and should

be avoided by all possible means. The modern view

is tolerant of uncertainty and considers that science

should deal with it because it is part of the real

world. This is especially relevant when the goal is to

FUZZY APPROACHES FOR MODELING DYNAMICAL ECOLOGICAL SYSTEMS

375

construct models. The fuzzy set theory, introduced

in (Zadeh, 1965), allow dealing with uncertainty in a

natural way, by means of the concept of objects that

have not precise boundaries (fuzzy sets). In this

paper three hybrid approaches of fuzzy systems are

used to model the global temperature change in the

earth, i.e. neuro-fuzzy systems, genetic-fuzzy

systems and the Fuzzy Inductive Reasoning

methodology.

3.1 Neuro-fuzzy Systems

A neuro-fuzzy system is a fuzzy system that uses

learning methods derived from neural networks to

find its own parameters, as the membership

functions of the input variables. In this work the

Adaptive Network based Fuzzy Inference System

(ANFIS) is used since is one of the more popular

neuro-fuzzy system reported in the literature (Jang,

1993). ANFIS is a function of the Fuzzy toolbox of

Matlab

ANFIS represents a Sugeno-type neuro-fuzzy

system in a five-layer feedforward network

architecture (see Fig. 2). The rule base must be

known in advance and ANFIS adjusts the

membership functions of the antecedents and the

consequence parameters applying a mixture of

backpropagation and least mean squares procedure.

The main characteristic of the Sugeno inference

system is that the consequent or output of the fuzzy

rules is not a fuzzy variable but a function, as shown

in equation (4).

(4)

This has the advantage that the fuzzy system

functions are differentiable and learning algorithms

based on gradient descendent methods are

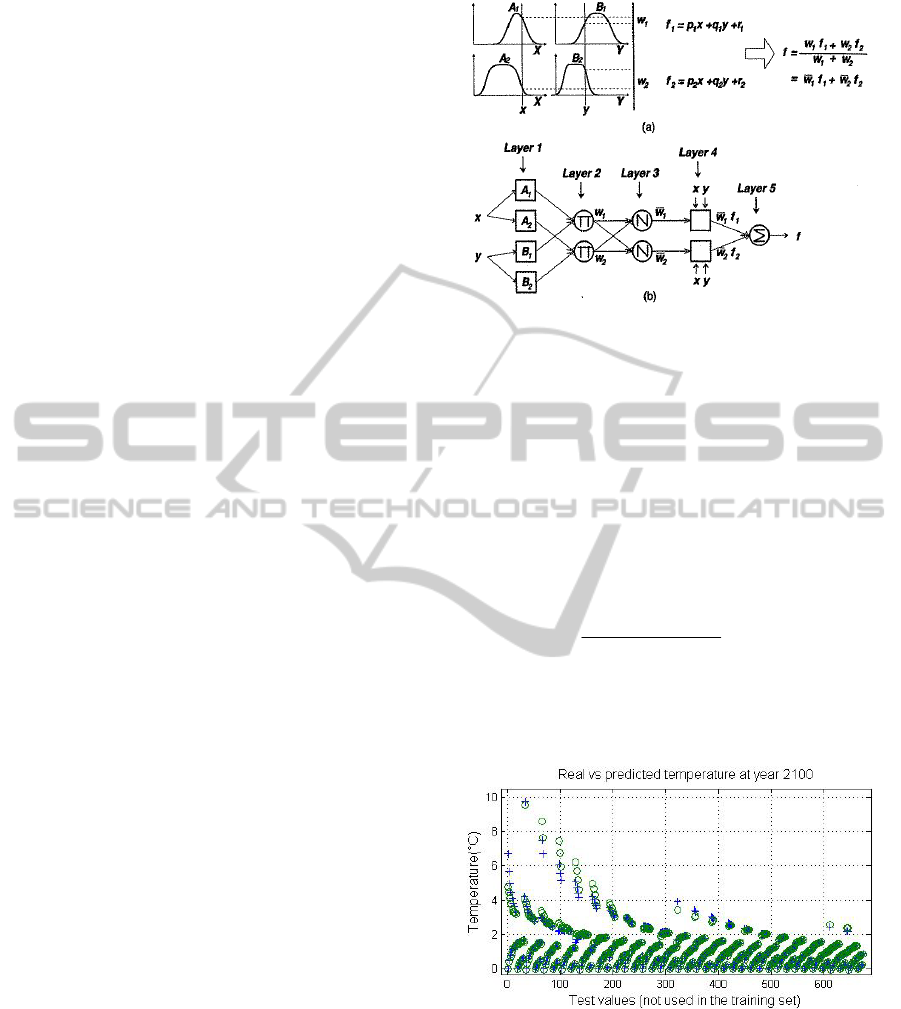
applicable. Fig. 2 shows the Sugeno type fuzzy

reasoning model (plot (a)) and its equivalent ANFIS

network structure (plot (b)).

In the application at hand the ANFIS model is

composed of 27 Sugeno rules, as the ones described

in equation (4), due to the fact that 3 membership

functions were used to represent the three input

variables. The ANFIS parameters are optimized by

using a set of 5395 data points obtained from the

experiment explained in section 2.

Figure 2: (a) Sugeno type fuzzy reasoning model. (b)

Equivalent ANFIS model. Figure extracted from (Jang,

1993).

The ANFIS model is validated by predicting the

temperature change of 674 data points not used for

training the model (also obtained from section 2.2).

ANFIS is able to predict very accurately the

temperature change test values, with a very low

normalized mean square error in percentage (MSE)

of 2.38%. The MSE is computed by means of

equation (5).





() ()

.100%

()

Eyt yt

MSE

VAR y t









(5)

where ŷ (t) is the predicted output, y(t) the system

output and VAR denotes variance. The real vs. the

predicted test data is shown in Fig. 3.

Figure 3: Real (‘

’) vs. Predicted (‘o’) test values when

using the ANFIS model to predict the temperature increase

at year 2100.

3.2 Genetic-fuzzy Systems

A Genetic Fuzzy System (GFS) is basically a fuzzy

system augmented by a learning process based on

evolutionary computation, which includes genetic

algorithms, genetic programming, and evolutionary

Rule

: If X is A

and Y is B

then f

= p

x + q

y + r

Rule

: If X is A

and Y is B

then f

= p

x + q

y + r

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

376

strategies, among other evolutionary algorithms

(Cordon et al., 2001). In this study three different

GFS based on iterative rule learning are analyzed,

i.e. TSK-IRL-R, MOGUL-TSK-R and MOGUL-

IRLHC-R. All of them are functions of the Keel

software (Keel, 2004).

In the iterative rule learning approach each

chromosome in the population represents a single

fuzzy rule, but only the best individual is considered

to form part of the final rule base. Therefore, it is

runed several times to obtain the complete

knowledge base. The advantage is that it reduces

substantially the search space, because in each

iteration only a fuzzy rule is searched. A

postprocessing stage is needed to force the

cooperation among the fuzzy rules generated in the

first stage.

3.2.1 TSK-IRL-R

The Iterative Rule Learning of Takagi–Sugeno-Kang

Rules (TSK-IRL-R) approach is a two-stage

evolutionary process to automatically learn

knowledge bases from examples (Cordon and

Herrera, 1999). The learning process is divided into

the generation and the refinement stages. The

generation stage allows to automatically deriving a

preliminary Sugeno knowledge base from the

training data set. It decides the number of rules and

determines their consequent parameters, generating

a locally optimal knowledge base. The refinement

stage takes the preliminary knowledge base obtained

in the previous stage and globally refines it by

tuning the antecedent membership function and

consequent parameter definition.

The generation process is based on a (μ, λ)-

evolution strategy, in which the fuzzy rules with

different consequents compete among themselves to

form part of the preliminary knowledge base. The

refinement process adapts the antecedents and

consequents of the fuzzy rules by means of a hybrid

evolutionary approach composed of a genetic

algorithm and an evolution strategy to obtain a set of

rules that cooperate in the best possible way.

The same training and data sets described before

are used for the TSK-IRL-R algorithm to obtain a

fuzzy model of the system under study. The mean

square error in percentage (MSE, described in

equation (5)), obtained when this model is used to

predict the test data set is 3.03%. This error,

although is slightly higher than the one obtained by

ANFIS, is quite low and the plot of the real vs. the

predicted test data looks really similar to the one of

ANFIS, presented in Fig. 3.

3.2.2 MOGUL-TSK-R

MOGUL is a Methodology to Obtain Genetic fuzzy

rule-based systems Under the iterative rule Learning

approach. This methodology is composed of some

design guidelines that will allow us to obtain genetic

fuzzy rule base systems (GFRBS) to design different

types of fuzzy rule bases, i.e. descriptive and

approximate Mamdani-type and Sugeno-type.

The MOGUL-IRLHC-R is a MOGUL approach

base in the Sugeno type of rules (Alcalá et al., 2007).

The main differences respect the TSK-IRL-R is that

in the first stage it performs a local identification of

prototypes to obtain a set of initial local semantics-

based Sugeno rules. On the other hand the

cooperation between rules is accomplished in the

second stage by means of a genetic niching-based

selection process to remove redundant rules and a

genetic tuning process to refine the fuzzy

parameters. The MOGUL-TSK-R approach

proposes to use Mamdani fuzzy rules as fuzzy

prototypes to identify a set of fuzzy subspaces

grouping data with similar behaviour. The

prototypes are then use to identify Sugeno fuzzy

consequences.

The same data sets used before are used to obtain

a MOGUL-TSK-R model of the global warming

problem. In this case the MSE (see equation (5))

obtained is 3.09%, equivalent that the one reached

with the TSK-IRL-R model.

3.2.3 MOGUL- IRLHC-R

The MOGUL-IRLHC-R algorithm is also an

iterative rule learning approach that uses the

MOGUL paradigm, but in this case the goal is to

learn constrained approximate Mamdani-type

knowledge bases from examples (Cordón and

Herrera, 2001). It consists of three stages: an

evolutionary generation process, a genetic

multisimplification process and a genetic tuning

process. The first stage generates a set of fuzzy rules

with constrained free semantics covering the training

set in an adequate form. The second stage performs

a selection of rules using a binary coded genetic

algorithm with a genotypic sharing function and a

measure of the fuzzy rule base system performance.

The idea is to remove redundant rules while

maximizing the cooperation among the staying rules.

The third stage performs a tuning based on a real

coded genetic algorithm and the previous

performance measure. It adjusts the membership

functions of each rule in each possible fuzzy rule

base derived from the multisimplification process.

FUZZY APPROACHES FOR MODELING DYNAMICAL ECOLOGICAL SYSTEMS

377

Then, the more accurate fuzzy rule based obtained is

the final output of the MOGUL-IRLHC-R

algorithm.

When applied to the problem at hand we obtain a

MSE of 10.08%. It is clear that the performance

decreases with respect the results obtained by the

approaches presented so far, i.e the genetic-fuzzy

systems and ANFIS.

3.3 Fuzzy Inductive Reasoning (FIR)

FIR methodology emerged from the general systems

problem solving (GSPS) architecture developed by

Klir (Klir and Elias, 2002). It is able to perform a

selection of the system relevant variables and to

obtain the causal and temporal relations between

them in order to infer the future behavior of that

system. It offers a model-based approach to

predicting either univariate or multi-variate time

series. A FIR model is a qualitative, non-parametric,

shallow model based on fuzzy logic. FIR is executed

under the Visual-FIR platform that runs under the

Matlab environment (Escobet et al., 2007).

The model identification function is responsible

for finding causal spatial and temporal relations

between variables that offer the best likelihood for

being able to predict the future system behavior

from its own past, thereby obtaining the best model.

The FIR model is composed by its structure or set of

relevant variables (called mask) and a set of

input/output rules that represent the systems’ history

behavior (called pattern rule base). A mask denotes a

dynamic relationship among qualitative variables.

The optimality of the mask is evaluated with respect

to the maximization of its forecasting power that is

quantified by means of a quality measure, based

mainly on the Shannon entropy. Once the best mask

has been identified, it can be applied to the

qualitative data matrices that were previously

obtained in the discretization process, resulting in a

pattern rule base.

Once the FIR model is available, a prediction of

future output states of the system can take place

using the FIR inference engine that is based on a

variant of the k-nearest neighbor rule, i.e., the 5-NN

pattern matching algorithm. The forecast of the

output variable is obtained by means of the

composition of the potential conclusion that results

from firing the five rules, whose antecedents best

match the actual state. The contribution of each

neighbor to the estimation of the prediction of the

new output state is a function of its proximity. A

detailed description of FIR methodology and Visual-

FIR platform can be found in (Nebot et al., 2003;

Escobet et al., 2007).

The same training and test data sets described in

the ANFIS section have been used for training and

test the FIR model. As explained before, in order to

obtain a FIR model it is first necessary to convert the

quantitative data into qualitative data by means of

the discretization function. In this case, all the 3

input variables are discretized into 3 classes, i.e.

low, medium and high, whereas the output variable,

is discretized into 5 classes, i.e. very low, low,

medium, high and very high, following the experts

knowledge. The optimal mask obtained is composed

of all the system input variables. Therefore, FIR

finds that all three input variables are important and

that there is not redundancy in them.

The FIR model obtained is very precise when it

is used to predict a test data set of 674 values, not

used in the training set. As can be seen in Fig. 4, the

real and the predicted values are almost

undistinguishable one from each other, being the

MSE extremely low, i.e. of 0.25%.

Figure 4: Real (‘

’) vs. Predicted (‘o’) test values when

using the FIR model to predict the temperature increase at

year 2100.

4 RESULTS AND DISCUSION

Table 1 summarizes the results obtained for each of

the fuzzy approaches presented in this paper when

applied to the global temperature change problem.

If we focus in the prediction performance it is

clear that the FIR methodology is the best one, much

better than the neuro-fuzzy and genetic-fuzzy

systems approaches. However, if we center in the

number of rules, ANFIS is the best choice because is

the one that captures the behavior of the system with

the lower number of rules.

It is also interesting to confirm that genetic

approaches need considerably much time than

ANFIS and FIR to learn de fuzzy rule bases.

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

378

Table 1: Results of all fuzzy approaches to the global

temperature change problem.

Method MSE #Rules Time

ANFIS 2.38% 27 15sec.

TSK-IRL-R 3.03% 50 50min.

MOGUL-TSK-R 3.09% 121 >60min.

MOGUL-IRLHC-R 10.08% 34 28min.

FIR 0.25% 56 5sec.

Therefore, it can be concluded that the different

fuzzy approaches used to model the global

temperature change problem are useful for the task

at hand, because all of them have a high level of

prediction accuracy. Depending on the users

interests it can be more desirable to choose a

methodology with high precision in the prediction,

like FIR, or a less precise model but with a small

number of rules in it, like ANFIS, MOGUL-IRLHC-

R or TSK-IRL-R.

This work is an initial attempt to compare

different types of fuzzy modeling approaches when

dealing with ecological systems. It does not pretend,

at this point, to be an exhaustive and rigorous

comparison, but to give a first inside into hybrid

fuzzy modeling of ecological problems. The next

step is to incorporate other fuzzy-based

methodologies, such is the LR-FIR, which is an

attempt to reduce the number of FIR rules obtained

while minimizing the loss of precision in the

prediction. Finally, we plan to study other ecological

problems mainly focused in climate systems.

5 CONCLUSIONS

This paper studies the usefulness of hybrid fuzzy

modelling approaches when dealing with a real

ecological system, i.e. the global temperature

change. A box model of the ocean-atmosphere, that

reproduces satisfactorily the wide range of

temperature increase reported by the IPCC, is used.

From the temperature increase calculated with

the box model, different hybrid fuzzy models are

built. Concretely, the ANFIS that is a neuro-fuzzy

system, the TSK-IRL-R, MOGUL-TSK-R and

MOGUL-IRLHC-R that are genetic-fuzzy systems

based on the iterative rule learning approach, and the

FIR methodology. All the models are able to predict

accurately the global temperature increase in the

year 2100. The fuzzy models presented in this paper

are simpler than the box model and are much more

understandable from a policy maker point of view.

REFERENCES

Alcalá, R, Alcalá-Fdez. J., Casillas, J., Cordón, O.,

Herrera, F., 2007. Local identification of prototypes

for genetic learning of accurate TSK fuzzy rule-based

systems. International Journal of Intelligent Systems,

22, 909-941.

Bloch, I., 2005. Fuzzy spatial relationships for image

processing and interpretation: a review. Image and

Vision Computing, 23(2), 89-110.

Cordon, O., Herrera, F., 1999. A Two-Stage Evolutionary

Process for Designing TSK Fuzzy Rule-Based

Systems. IEEE Transactions On Systems, Man, And

Cybernetics—Part B: Cybernetics, 29 (6).

Cordon, O., Herrera, F., 2001. Hybridizing genetic

algorithms with sharing scheme and evolution

strategies for designing approximate fuzzy rule-based

systems. Fuzzy sets and systems, 118, 235-255.

Cordon, O., Herrera, F., Hoffmann, F., Magdalena, L.,

2001. Genetic Fuzzy Systems. Evolutionary Tuning

and Learning of Fuzzy Knowledge Bases. Vol. 19 of

Advances in Fuzzy Systems - Applications and

Theory. World Scientific.

Escobet, A., Nebot, A., Cellier, F. E., 2008. Visual-FIR: A

tool for model identification and prediction of

dynamical complex systems. Simulation Practice and

Theory, 16, 76-92.

IPCC, 2007. Climate Change. Cambridge University

Press.

Jang, J.R., 1993. ANFIS: Adaptive-Network-Based Fuzzy

Inference System. IEEE Transactions on systems, man

and cybernetics, 23 (3).

Keel Platform,2004. http://sci2s.ugr.es/keel/developpment.

php.

Klir, G. J., Elias, D., 2002. Architecture of Systems

Problem Solving,Plenum Press. New York, 2

edition.

McGuffie, K., Henderson-Sellers, A., 2005. A Climate

Modelling Primer. Third Edition. Wiley.

Nebot, A., Mugica, F., Cellier, F. E., Vallverdu, M., 2003.

Modeling and Simulation of the Central Nervous

System Control with Genetic Fuzzy Models.

Simulation: Society for Modeling and Simulation

International, 79(11), 648-669.

Watanabe, K., Izumi, K., Maki, J., Fujimoto, K., 2005. A

Fuzzy Behavior-Based Control for Mobile Robots

Using Adaptive Fusion Units. Journal of Intelligent

and Robotic Systems, 42(1), 27-49.

Wigley, T. M. L., Schlesinger, M. E., 1985. Analytical

solution for the effect of increasing CO2 on global

mean temperature. Nature, 315, 649-652.

Williams, P. D., 2005. Modelling climate change: The role

of unresolved processes. Phil. Trans. R. Soc. A, 363,

2931-2946.

Zadeh, L. A., 1965. Fuzzy Sets. Information and Control.

8(3), 338-353.

FUZZY APPROACHES FOR MODELING DYNAMICAL ECOLOGICAL SYSTEMS

379