MODELING THE EFFECT OF HYDROGEN ON CREEP

BEHAVIOR OF ZIRCALOY CLADDING

VenkatRao Mallipudi, Stéphane Valance and Johannes Bertsch

Laboratory for Nuclear Materials, Paul Scherrer Institut, 5232 Villigen, Switzerland

Keywords: Dry storage, Zircaloy, Creep, Hydrogen, Hydride.

Abstract: During dry storage of used nuclear fuel, creep is the most likely degradation mechanism for the zirconium

alloy fuel cladding. The cladding integrity during dry storage depends on the internal fuel rod pressure, the

temperature, the amount of oxidation, irradiation hardening and the content of hydrogen which has been

taken up during in-reactor operation. In this paper, the effect of hydrogen on the creep behavior of zirco-

nium alloy cladding material was investigated at the temperature of 400°C. Depending on temperature, hy-

drogen can be found in the material under the form of solid solution and/or precipitated hydride. To capture

this phenomenon, a numerical mesoscale model of the hydrogenated material has been built using the Finite

Element (FE) method. The numerical setup explicitly describes the hydrides as an inclusion in a hydroge-

nated matrix. The matrix creep behavior follows combined Norton-Bailey creep rules whereas the hydrides

are considered to be elastic material. The creep law was defined in FE Code ABAQUS using the user sub-

routine CREEP. The comparison of predicted creep behavior obtained from FE showed good agreement

with the results reported in literature. Particularly, our model is able to seize the competition between the

creep strain rate enhancement induced by hydrogen in solid solution and its reduction due to precipitated

hydrogen.

1 INTRODUCTION

Zirconium alloys are used as cladding material for

nuclear fuel in Light Water Reactors (LWRs) be-

cause of the low thermal neutron capture cross sec-

tion of zirconium, the good mechanical properties

and limited corrosion. The fuel cladding is the first

barrier against release of radionuclides and its inte-

grity is therefore essential. In order to maintain the

integrity, assessment of all relevant degradation and

failure mechanisms need to be considered (Rosen

and O'Connell, 1994). Dry storage is the solution

used by many facilities worldwide in order to in-

crease their storage capacity while awaiting a peren-

nial storing solution. During dry storage creep is one

of the degradation mechanisms for used fuel clad-

ding, as an excessive creep strain may lead to an

eventual ductile fracture (Blackbum et al., 1978).

The creep strain is limiting the possible life time,

during dry storage as well as dictating the maximum

allowable temperature in order to maintain the inte-

grity of the cladding. Therefore the integrity of used

fuel cladding during dry storage has been evaluated

by predicting its creep behavior. Mayuzumi and

Onchi (Mayuzumi and Onchi, 1990) proposed an

empirical creep model, which covers a wide temper-

ature range to be used under long-term storage con-

ditions. In the reactor environment, hydrogen is

generated in coolant water due to oxidation of Zry-4

or radiolysis, and diffuses into the cladding material.

Depending upon the temperature i.e. Terminal Solid

Solubility for Dissolution (TSSD), hydrogen can be

found in the material under the form of solid solu-

tion or/and precipitated hydrides. For example the

solubility limit of hydrogen in Zry-4 is about

170 ppm at 400°C (Rui and Xiaoxue, 2009) and

excess hydrogen forms zirconium hydrides. In the

framework of continuum mechanics, hydrides preci-

pitates in the α-Zr can be viewed as a metal-matrix

composite.

Among the different variations of zirconium al-

loys, the so-called Zircaloy-4 (Zry-4) is used as

cladding material for fuel in Pressurized Water Re-

actors (PWRs). The creep strain rates of Zry-4 under

annealed condition (annealed at 650°C for 4 hours)

show an increase when hydrogen is in solid solution

and a decrease when part of the hydrogen precipi-

tates as hydrides (Rupa et al., 2002). Setoyama and

293

Mallipudi V., Valance S. and Bertsch J..

MODELING THE EFFECT OF HYDROGEN ON CREEP BEHAVIOR OF ZIRCALOY CLADDING.

DOI: 10.5220/0003615402930299

In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2011), pages

293-299

ISBN: 978-989-8425-78-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Yamanaka (Setoyama and Yamanaka, 2004) studied

the effect of hydrogen on creep behavior of zirco-

nium and Zry-4 using the indentation technique.

They observed an increase in the creep rate with the

addition of hydrogen when hydrogen is in the form

of solid solution. In addition, they stated that the

creep exponent is independent of hydrogen content

and the increase in creep rate is due to the change in

the Young’s modulus with hydrogen Yamanaka et

al., 2002).

Since the Zry-4 cladding material is subjected to

stress for long periods of time at elevated tempera-

tures, a thorough knowledge of creep behavior is

required for their engineering applications. How-

ever, costly and time consuming creep experiments

make it difficult to experimentally assess the creep

behavior of the cladding. Therefore, the develop-

ment of analytical and/or numerical approaches for

predicting the creep behavior is indispensable. How-

ever, the analytical models cannot directly represent

the actual creep behaviors of the heterogeneous

materials, because the local state of stress and strain

in the matrix is highly heterogeneous in nature.

On the other hand, numerical methods such as

the FE Method enable to evaluate the micro-

mechanical/meso-mechanical behaviors during the

creep of the heterogeneous materials, since they can

successfully model the time-dependent problems and

local stress field. Numerous reports can be found in

the literature explaining the numerical studies re-

lated to the creep behavior of heterogeneous materi-

als (Dragone and Nix, 1992, Sørensen et al., 1993

and Sabbah and Essam, 2007). Dragone and Nix,

Sørensen et al. developed numerical frameworks for

stress analysis and prediction of creep behavior of

metal matrix composites by using unit cell model-

ing. The creep behavior of magnesium alloys rein-

forced with short fibers was numerically determined

by Sabbah and Essam, using simple idealization of

the composite material. In their work, modeling was

carried out using three relationships describing sepa-

rately the three stages (i.e. primary, secondary and

tertiary) of the creep behavior of magnesium alloys.

The present paper focuses on the influence of

hydrogen in solid solution and hydrides precipitates

at 400°C on the creep behavior of Zry-4 using a

numerical modeling approach. The Zry-4 is consid-

ered as annealed and in sheet form. Thus, the result-

ing behavior may differ from that of typical Zry-4

tubes being used as cladding material and exhibiting

high deformation and thus residual stresses.

2 NUMERICAL MODELING

2.1 Creep Constitutive Law

The creep constitutive law for describing the creep

behavior of the Zry-4 matrix is similar to the one

used for magnesium alloys (Sabbah and Essam,

2007). An empirical relationship is applied for each

creep stage of the creep curve (primary, secondary).

A mathematical relationship for the description of

the creep behavior up to the secondary stage could

be achieved by combining these two relations as

follows:

vpeffc

AtmA

σσε

−1



(1)

where

effc,



is the effective creep strain rate, σ

the von Mises stress, t is the time, and m, A

, A

, n

and n

are material constants. The first term (Norton-

Bailey) on the right-hand side of equation (1)

represents the primary creep and the second term

(Norton) describes the secondary state creep strain.

According to Setoyama and Yamahaka, the

change in creep strain with presence of hydrogen in

the form of solid solution is due to change of

Young’s modulus. The change in Young’s modulus

of Zry-4 as function of hydrogen content up to the

TSSD is given by the equation (2) by Yamanaka et

al. (Yamanaka et al., 2002) as follows:

,)..10518.21(

ECE

−

×−=

(2)

where E

is Young‘s modulus of Zry-4 with hydro-

gen in the form of solid solution at the content C

(ppm), and E

is Young‘s modulus of the material

without hydrogen.

Thus, the creep coefficients as a function of hydro-

gen content A

and A

can be written as follows:

.)].10518.21[(.

,)].10518.21[(.

−

×−=

HssH

HppH

CAA

and

(3)

To predict the creep behavior of Zry-4 with the

presence of hydrogen in the form of solid solution,

in the present work, equation (1) with the modified

creep coefficients according to the equation (3) is

used. While for further increase of hydrogen content

(hydrogen is precipitated in form of hydrides), a

numerical mesoscale model of the hydrogenated

material has been built using the FE method. The

numerical setup explicitly describes the hydrides as

an inclusion in a hydrogenated Zry-4 matrix. The

creep behavior the hydrogenated Zry-4 matrix fol-

lows a combined Norton-Bailey and Norton creep

rule equation (1) and its creep strain coefficients are

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

294

defined according to the equation (3), whereas the

hydrides are considered to be elastic material. The

creep law was implemented in FE code ABAQUS

using the user subroutine CREEP.

2.2 Details of Hydrided

Zircaloy- 4 a - Finite Element

Modeling.

Hydrided Zry-4 consists of the idealized, untextured

hydrogenated matrix (i.e. hydrogen up to TSSD limit

dissolved in Zry-4 matrix) and precipitated hydrides.

The size of the hydrided Zry-4 considered in the

present work is 600 μm x 600 μm as the thickness of

the cladding material is approximately 600 μm. The

distribution of hydrides is assumed to follow the

symmetries about the radial and transverse axes,

hence in the present work, one quarter of the hy-

drided Zry-4 was modeled (300 μm x 300 μm). It

was also assumed that all the hydrides are δ type

(Daum et al., 2009) and that the bonding between

hydrides and Zry-4 matrix is perfect. The orientation

and length distribution of hydrides have been taken

from scaling the measured real hydride distribution

in a cladding tube (

Valance et al., 2010). The thickness

of the hydrides considered is 0.5 μm. The FE simu-

lation code ABAQUS was used to carry out the

finite element modeling and analysis. The hydrided

Zry-4 was discretized, using four-noded plane stress

solid elements with reduced integration (CPS4R).

After checking for convergence, approximately

45000 elements and 65000 nodes were used in the

FE mesh. The hydrogenated Zry-4 matrix was con-

sidered as elasto-plastic with creep, while hydrides

were considered as elastic bodies. The material

properties of non-hydrogenated Zry-4 matrix were

taken from the literature (Puls et al, 2005). The elas-

tic properties of the hydrides were assumed to be the

same as for Zry-4 matrix, as reported in the literature

(Nho et al., 1989), at room temperature the mechani-

cal properties of solid hydrides remain about the

same as the original zirconium alloy and decrease

with temperature at about the same rate as the zirco-

nium alloy. The Young’s modulus and Poisson’s

ratio at 400°C are 74.78 GPa and 0.346, respective-

ly. The creep parameters used here for non-

hydrogenated Zry-4 are A

4.06x10

-14

MPa

-n

-1

= 9.16x10

-19

MPa

-n

-1

, n

= 5.2

= 6.97 and m =

0.34

obtained experimentally in this study (not re-

ported here). The Young’ modulus E

and creep

coefficients (A

and A

) for the hydrogenated Zry-

4 matrix were estimated according to the equations 2

and 3.

In order to predict the creep behavior, finite ele-

Figure 1: Hydrided Zry-4 (hydrogen content = 500ppm)

with boundary conditions.

ment calculations were performed in two steps: first,

the stress field in the hydrogenated Zry-4 matrix and

hydrides is calculated for a given initial tensile stress

in terms pressure (equal to the stress) using a nonlin-

ear elastic-plastic calculation at time t = 1x10

-10

hour. The stress is then kept constant and subsequent

time-dependent creep analyses were performed. The

large strain FE model is employed by invoking the

NLGEOM option within ABAQUS. Figure 1 illus-

trates the boundary condition for the FE analysis.

The average creep strain versus time curve was

computed by taking the ratio of average elongation

at the load application region (see Figure 1) to the

original length of microstructure.

3 RESULTS AND DISCUSSION

Figure 2 depicts the von Mises stress distribution of

hydrogenated Zry-4 matrix for a hydrogen content of

500 ppm initially and after 250 hours at 400°C under

a stress of 120 MPa. From this figure it can be ob-

served that the von Mises stresses are reduced in the

matrix as a consequence of the compressive stresses

induced in the matrix during creep. Though there is

a slight increase in local stresses (131 MPa to

147 MPa) the reduction in stress around the hydrides

is much higher. The von Mises stress in the matrix

around the hydrides was initially about 115 MPa for

an applied stress of 120 MPa, and is reduced to

58 MPa after 250 hours. The reduction in stress is

about 50%. As the equivalent stress level is de-

creased, the creep strain rate decreases. The magn-

tude of stress depends on the distribution and quanti-

ty of hydrides in the hydrogenated matrix.

MODELING THE EFFECT OF HYDROGEN ON CREEP BEHAVIOR OF ZIRCALOY CLADDING

295

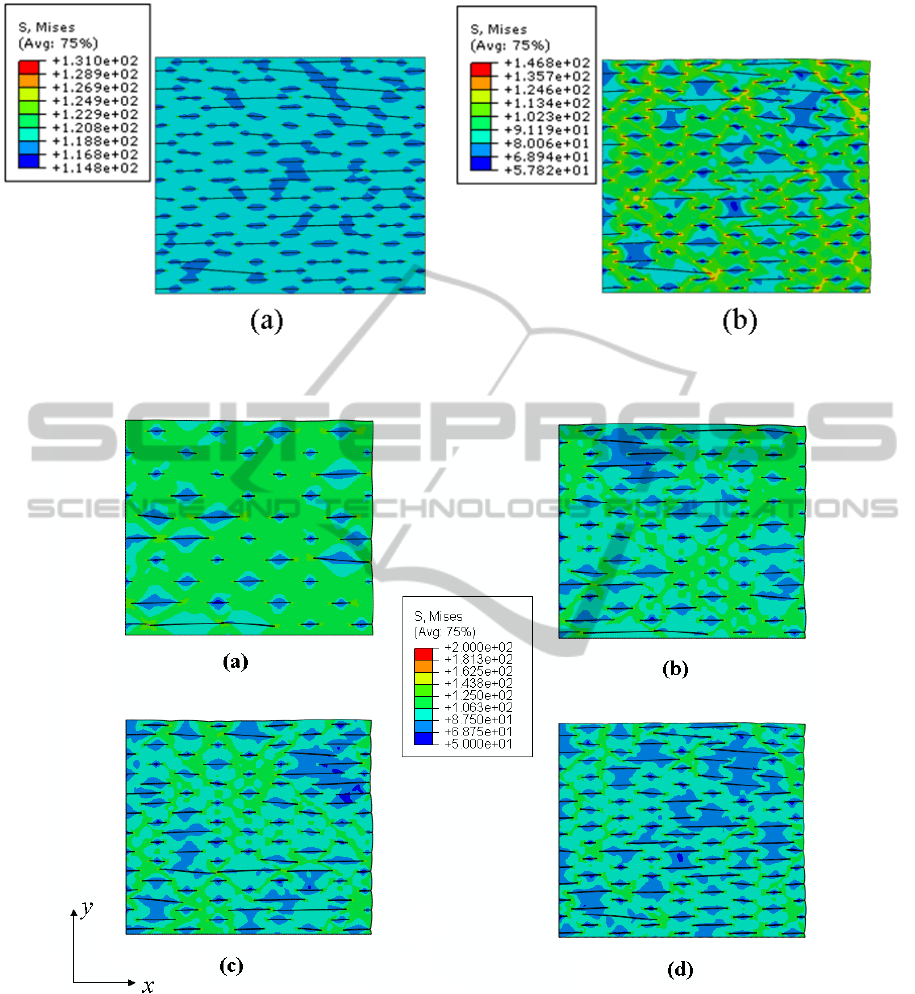
Figure 2: von Mises stress distribution of sample with a 500 ppm loaded under 120MPa at 400°C; (a) initially and (b)

250 hours von Mises stress filed (stress direction according to figure 1).

Figure 3: von Mises stress distribution at 250 hours, creep duration for different hydrogen contents, (a) 300 ppm, (b)

400 ppm, (c) 450 ppm and (d) 500 ppm (stress direction according to figure 1).

and the creep strain dropped to 4.05% when the

hydrogen content was 500 ppm. The comparison of

creep strain without hydrogen and with 170 ppm

hydrogen content shows a relative increase of creep

strain by 28%, whereas the creep strain without

hydrogen and with 500 ppm hydrogen content shows

a relative decrease of 51%. At a hydrogen content of

240 ppm, the same creep strain as for a Zry-4 with

out hydrogen was predicted.

Figure 3 shows the von Mises stress after

250 hours at 400°C and under a stress of 120 MPa

for different hydrogen contents. From this figure it

can be seen that the von Mises stress in the matrix

decreases with increase of hydrogen content, which

leads to a reduction in creep strain.

The overall creep strain as a function of time for

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

296

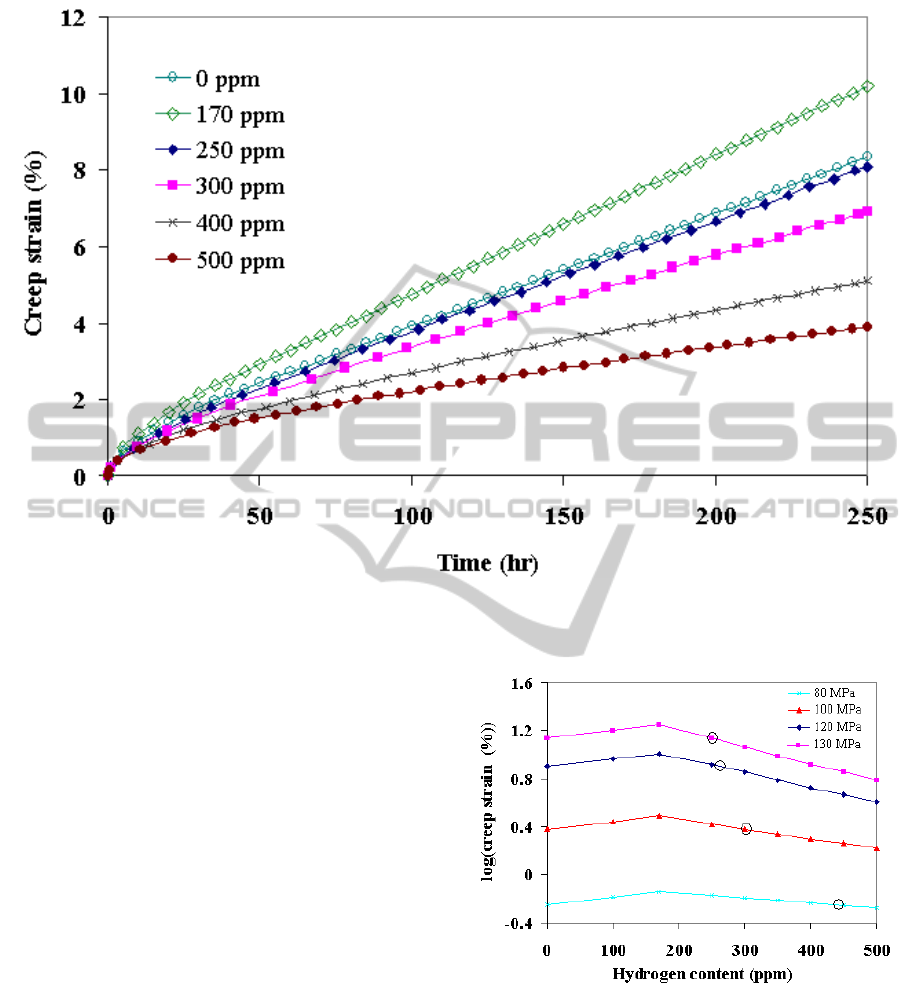
Figure 4: Creep strain versus time for different hydrogen contents.

different hydrogen content and creep strain after

250 hours is shown in figure 4. The creep strains

increases with the increase of hydrogen content up

to the TSSD, thereafter decreases for further in-

crease of hydrogen content. Similar behavior was

reported in the literature by Rupa et al., 2002. After

250 hour the maximum creep strain was found to be

10.23% when the hydrogen content was170 ppm

(corresponding to TSSD for temperature 400°C),

A similar trend in creep behavior is observed for

the other stress levels studied in this work. The creep

strains (on log scale) at 250 hours at a temperature

of 400°C and under different applied stresses

(80 MPa, 100 MPa, 120 MPa and 130 MPa) are

shown in figure 5. The creep strain increases with

stress magnitude, however, the hydrogen content at

which the creep strain equals the one for Zry-4 with-

out hydrogen decreases with an increase of the ap-

plied stress (indicated by the small circles in fig-

ure 5). The hydrogen content at which this is the

case is 442 ppm at 80 MPa, 302 ppm at 100 MPa,

262 ppm at 120 MPa and 251 ppm at 130 MPa.

Figure 6 shows the variation of the steady state

creep rates as a function of hydrogen content for

different applied stress values. The curves show that,

as expected for all the hydrogen contents below the

solubility limit, the steady state creep strains are

higher for higher applied stresses.

Figure 5: Creep strain (on log scale) at 250 hours as a

function of hydrogen content for different applied stresses;

the circles indicate the hydrogen contents for the same

creep strain as without hydrogen.

It can also be observed that the drop in steady

state creep rate is higher for higher applied stress

when the hydrogen content increases from 250 ppm

to 500 ppm. For a stress of 130 MPa, the drop in

steady state creep rate is about 68%, whereas the

drop is about 33% for a stress of 80 MPa. From

MODELING THE EFFECT OF HYDROGEN ON CREEP BEHAVIOR OF ZIRCALOY CLADDING

297

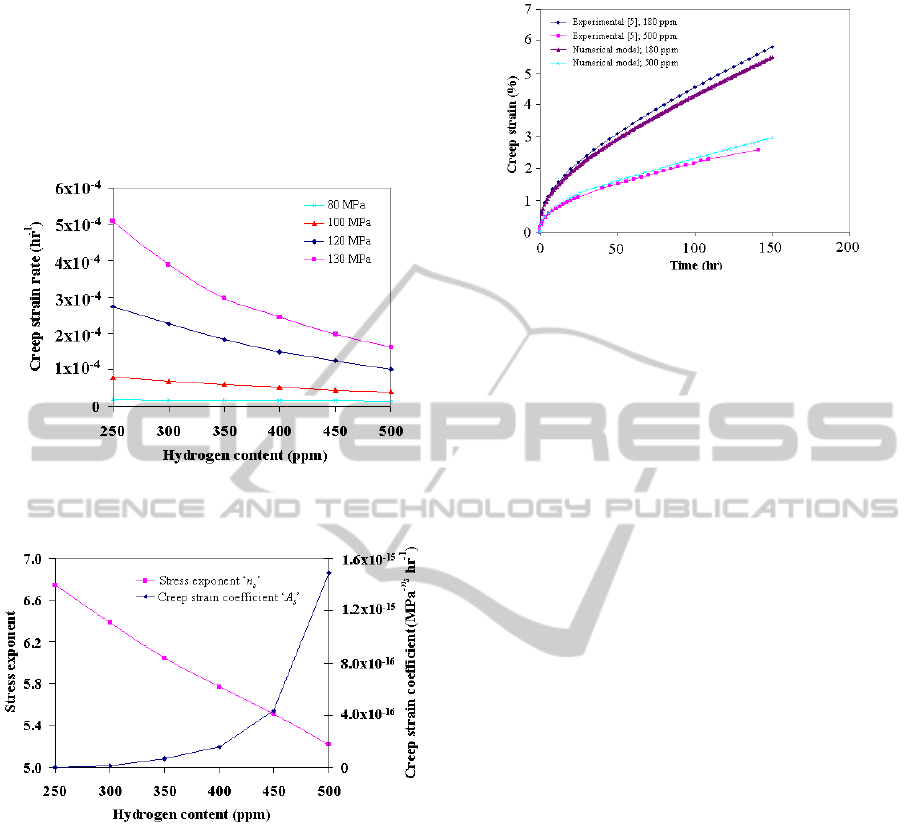
these steady state creep rates, the equivalent steady

state creep parameters are estimated. The equivalent

steady state creep parameters as a function of hydro-

gen content are depicted in figure 7. The stress ex-

ponents decrease linearly with the increase of the

hydrogen content, while the creep coefficients show

an exponential increase with hydrogen content.

Figure 6: Steady state creep strain rate as a function of

hydrogen content.

Figure 7: Steady state creep stress exponent (ns) and creep

strain coefficient (As) as a function of hydrogen content.

4 COMPARISON OF PRESENT

RESULTS AND LITERATURE

In order to validate the present model, it is attempted

to compare the calculated creep curves for Zry-4

with hydrogen contents of 180 ppm and 500 ppm

with those published by Rupa et al., 2002. Figure 8

reveals a good agreement of the creep curves ob-

tained in this present work and from literature.

Figure 8: Comparison of creep strain versus time curves

obtained by present work and literature Rupa et al., 2002

for two hydrogen contents.

5 CONCLUSIONS

In this paper a numerical model was proposed to

investigate the effect of hydrogen on the creep beha-

vior of Zry-4. This zirconium alloy being used as

tube cladding for nuclear fuel, the material has been

considered here as texture-free and in sheet form.

The creep behavior of hydrided Zry-4 is analyzed by

the Finite Element Method.

For all applied stresses, the creep strain increases

with increase of the hydrogen content up to TSSD,

and decreases for a further increase of the hydrogen

content. As the level of applied stress increases, the

hydrogen content for the same creep strain without

hydrogen decreases.

The stress exponent decreases linearly with in-

crease of hydrogen content, while the creep coeffi-

cient value shows an increase exponentially with

increase of hydrogen content. A comparison of pre-

dicted creep curves obtained from the present work

with the creep curves reported in literature showed

good agreement.

REFERENCES

Rosen, R. S., O'Connell, W. J., 1994. Lawrence Livermore

National Laboratory, Livermore, CA 94550 USA.

Blackbum, L. D., Ferwick, D. G., Fields, S. R., James, L.

A., Moen, R. A., 1978. Hanford Engineering Devel-

opment Laboratory Report, HEDL-TME 78-37.

Mayuzumi, M., Onchi, T., 1990. Journal of Nuclear Mate-

rials. 171 381-388.

T. Rui, T., Xiaoxue, Y., 2009. International Journal of

hydrogen energy. 34 7269–7274

Rupa, N., Clavel, M., Bouffioux, P., Domain, C., A. Le-

gris, A., 2002. Zirconium in the Nuclear Industry 13th

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

298

International Symposium, ASTM STP 1423, ASTM In-

ternational, West Conshohocken, PA, (2002) 811-836

Setoyama, D., Yamanaka, S., 2004. Journal of Alloys and

Compounds, 379(2004)193-197.

S. Yamanaka, S., M. Kuroda, M., Setoyama, M., 2002

Trans. Atomic Energy Soc. Japan. 1 4 (2002) 323-328.

Dragone, T. L., Nix, W. D., 1992. Acta Metall. Mater.

40(12)(1992) 2781-2788.

Sørensen, N. J., 1993. Acta Metall. Mater. 41 (10) (1993)

2973-2982.

Sabbah, A., Essam, E., 2007. Computational Materials

Science 39 (2007) 155–159

Daum, R. S., Chu, Y. S., Motta, A.T., 2009. Journal of

Nuclear Materials 392 (2009) 453–463

Valance, S., Bertsch, J., Alam, A. M., 2010. Journal of

ASTM International (JAI) (2010) – accepted/in press

Puls, M. P, San-Qiang Shi., Rabier, J., 2005. Journal of

Nuclear Materials 336 (2005) 73–80

Nho, K., Choi, S., Lee, B., 1989. Journal of the Korean

Nuclear Society 336 (1989) 111–122

MODELING THE EFFECT OF HYDROGEN ON CREEP BEHAVIOR OF ZIRCALOY CLADDING

299