COMPREHENSIVE EVALUATION OF THE RAILWAY

PASSENGER’S SATISFACTION BASED ON ROUGH SET

AND ENTROPY

Feng Yun-qing, Li Xue-wei

School of Economics and Management, Beijing Jiaotong University, Haidian District, 100044 Beijing, China

Li Xue-mei

School of Economics and Management, Beijing Jiaotong University, Haidian District, 100044 Beijing, China

Keywords: Satisfaction, Rough Set, Entropy Method, Weight.

Abstract: To assess the passenger’s satisfaction is the key to analyze the service quality of the railway sector. The

most important part of the assessment is to calculate the weight of each index which influences the

passenger’s feelings in their journey. In this paper, we choose Ticket Price, Convenience, Train speed,

Comfort and Security as the indicators to assess the passenger’s satisfaction. First, we use the rough set

theory to calculate the subjective weight of the five indicators that influences the passenger’s travel feelings.

Second, we calculate the objective weight of the same five indicators using the Entropy Method. At last, we

get the integrated weight based on the subjective weight and the objective weight through the integrated

weight calculating formula. The results indicate that the Security has the highest weight, followed by the

weight of the Ticket Price and the Convenience. The Comfort and Speed have the lowest weight.

1 INTRODUCTION

With the development of the society, Customers

have a higher requirement on the quality of their

travel. They will also have more needs in their

travel. So to meet the demand of the tourists is to

make visitors get the most satisfaction. For the

railway enterprises, improving the railway

passenger’s satisfaction not only can increase the

passenger’s loyalty in the railway transportation, but

also can bring more passenger, which can bring high

profits to the railway transport enterprise. Therefore,

to assess the railway passenger’s satisfaction can

reasonably improve the railway transport

enterprise’s service quality and level. What’s more,

it can also improve the passenger’s travel

satisfaction which can bring more income for the

transport enterprise.

2 RESEARCH STATUS

The most important part to assess the railway

passenger’s satisfaction is to ascertain each factor’s

weight which affects the passenger’s travel quality.

There are mainly two types of methods that can

ascertain the factors’ weight. These are the

subjective weighting method and the objective

weighting method. The subjective weighting method

mainly involves the AHP method, G1 method and

the expert weighting method, etc. The objective

weighting method mainly includes the principal

component analysis, entropy method and the rough

set theory and so on. These two types of methods

have their own characteristics and defects. The

subjective weighting method is mainly based on the

decision-makers’ knowledge and experience to

decide the factors’ weight, which generally

consistent with the common sense. But this method

has some subjectivity and arbitrariness, so it will

affect the accuracy and reliability of the decision.

The objective weighting method is mainly based on

629

Yun-qing F., Xue-wei L. and Xue-mei L..

COMPREHENSIVE EVALUATION OF THE RAILWAY PASSENGER’S SATISFACTION BASED ON ROUGH SET AND ENTROPY.

DOI: 10.5220/0003616506290635

In Proceedings of the 13th International Conference on Enterprise Information Systems (PMSS-2011), pages 629-635

ISBN: 978-989-8425-56-0

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

the correlation between each index to calculate the

weight according to a certain mathematical model.

The advantage of this method is that it fully

exploited the original data’s information. The

evaluation results have a strong theoretical basis and

are more close the reality. But this method ignored

the decision-makers’ knowledge and experience,

which will have certain deviations to the

decision-makers’ feeling. Therefore, we usually use

the comprehensive evaluation method based on the

subjective weighting method and the objective

weighting method to calculate each factor’s weight.

Wu Chun-you and Liu Yan

use the

comprehensive evaluation method based on the G1

method and the entropy method to determine the

weight of the factors that impact the interests of the

city-renewable resources (Wu Chun-you, Liu Yan,

2010). Ma Xiao-ying

uses the entropy method to

assess the readers’ satisfaction in the university

library and gets the weights of different factors that

affect the readers’ satisfaction (Ma Xiao-ying,

Zhang Guo-hai, Han Shu-fen, 2007). Song Li-min

also uses the comprehensive evaluation method

based on the AHP method and the entropy method to

get the weight of different indicators between

different readers (Song Li-min, 2009). Meng Ming

uses the same comprehensive evaluation method to

assess the power customer satisfaction and get the

weights (Meng Ming, Niu Xiao-dong, Gu Zhi-hong,

2005). Peng Jin-shuan uses the comprehensive

evaluation method based on the entropy method and

the subjective weighting method to evaluate the

passenger’s satisfaction to the urban public transport

and get each factor’s weight (Peng Jin-shuan, Hao

Yi-ming, Peng Li-fang, 2007).

Some scholars use the rough set theory to

evaluate the weight of different factors. Xiong Ping

proposed a new subjective weighting method based

on the information concept in rough set (Xiong Ping,

Cheng Hua-bin, Wu Xiao-ping, 2003). They

established a comprehensive optimization model to

determine the weight based on the optimization

theory. Hao Cheng uses the rough set theory to

research the weight of the effectiveness factors in

the urban rail transit project. Furthermore, they

obtained the combined weights of multiple factors

(Hao Cheng, Li Jing, Li Xue-Mei, Li Xue-wei,

2008).

Up to now, no one has used the rough set theory

to evaluate the railway passenger’s satisfaction.

Furthermore, no one has used a method based on the

rough method and the entropy method the get the

in-depth assessment for the railway passenger’s

satisfaction. First, this paper will use the rough set

theory to ascertain the factors’ subjective weight that

affects the passenger’s satisfaction. And then use the

entropy method to calculate the factors’ objective

weight. Finally, we use the comprehensive weight

formula

(Liu Jie, Li Chao-feng, Li Xiao-peng, Wen

Bang-chun, 2008) to calculate each factor’s weight

so that we can know the degree of different factors

that influence their travel choice.

3 THE SUBJECTIVE METHOD

BASED ON ROUGH SET

The rough theory, which was proposed by the Polish

mathematician Z. Pawlak in 1982, was a

mathematical method that research the

expression,learning and induction of the imprecise,

uncertain and incomplete data (China Research

Center of Industrial Safety in Beijing Jiaotong

University, 2009). The key points of this method to

blend classification and knowledge together and

then classify the data in the form of equivalence

because the knowledge comes from the human and

other species’ classification ability. The main idea of

this method is to deduce the decision-making and

classification rule of the problem through the

knowledge reduction on condition that the

classification ability doesn’t change. This method

was widely used in data analysis, data mining and

knowledge classification and other fields. This

theory which attracted wide attention from scholars

around the world in the 1990s in the 20th century

was successfully applied in the field of data analysis

and decision making, pattern recognition, machine

learning and knowledge discovery, etc.

3.1 Knowledge Definition

According to the rough set theory, a knowledge

representation system “S” can be expressed by

describing the attributes and the attribute values of

the research object (Chun-bao Chen, Li-ya Wang,

2006). So we define a equation:

(, ,,)SUCDVf 

In this formula,





,,Uxx 

means a collection

of objects.





,,Ccc 

means the subjects of

the condition attributes set.





,,Ccc 

means

the subjects of the decision attributes set. And the

conditions are

CDA





and

.CD

the collection of the attribute set.

UA V

an information function which gives each attribute

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

630

of the object an information value.

3.2 Indiscernible Relation

Suppose

is a series of equivalence relation in

So the

/UR

means all the equivalence class of

or the sets formed by the division of

. If

R

and

P 

, then the intersection of all the

equivalence relation in

is also a equivalence

relation. We call this relation an indiscernible

relation in

. We record it as

().IND P

3.3 Upper and Lower Approximation

For a given knowledge

(,),

UR

X 

U

and

()RINDK

, then we call





/|RX Y U R Y X 

the lower approximation

about

and we call





/|RX Y U R Y X 

the upper

approximation of

about

3.4 Positive, Negative and Border-field

For a given knowledge

(, ,,)SUACDVf

We suppose

is a nonempty universe and

is a

nonempty condition attribute set.

C

and

dD

we call









() | / ()

os d BX X U ind d

to be the

relative positive field of the decision attribute

for

The

()

neg X U RX

is the negative

field of

for

. The set

()

bn X RX RX

the border-field of

3.5 Weight Formula based on Rough

Set

Suppose

(, ,,)SUACDVf

is an

information system. The importance degree of the

condition attribute

can be expressed as follows.



()

() 1

()

Cc i

Card Pos D

Sig c

Card Pos D









(a)

cC

and

1, 2, 3, ,in 

stands for the

number of the elements in the attribute set

()

Pos D

stands for the collection of objects that

can be accurately divided into the equivalence class

of relations

according to the information of

classification

/UC

()

Pos D



stands

for the collection of objects that can be accurately

divided into the equivalence class of relations

according to the information of classification

/( )

UCc

[]Card

stands for the number of

the elements in the set.

We normalize the importance degree data of each

attribute according to the formula and get the weight

of each attribute. The results are as follows.

()

Cc i

Sig c







(b)

4 ENTROPY METHOD

4.1 The Definition of Entropy

Entropy is a concept derived from thermodynamics

(China Research Center of Industrial Safety in

Beijing Jiaotong University, 2009). Shannon,

founder of the information theory, used the entropy

theory to describe the uncertainty of the source

signal for the first time in 1948. Now this method is

widely used in the engineering, socio-economic and

other fields. Shannon gives the definition of the

source’s information entropy to us by the

probabilistic method. The definition of the

information entropy is as follows:

The System may be in

different states, and

the probability of each state is

(1,2,,)in 

. If



and





, the entropy of the system

Hpp







(c)

The entropy is a measure of the degree of

disorder on the system and the information entropy

is a measure of the degree of order on the system.

The smaller the value of the index’s information

entropy is, the greater the variability is. Therefore,

we can use the information entropy to calculate the

weight of each index by

the

variation of each

indicator.

4.2 Entropy Calculation Steps

In a system with

indexes and

objects, the

steps of the entropy calculation

( Don-Lin Mon,

Ching-Hsue Cheng, Jiann-Chern Lin, 1994; Hong

Zhang, Chao-lin Gu, Lu-wen Gu, Yan Zhang, 2011.)

are as follows:

(1)

The Standardization of the indexes membership

matrix. The valuation value of the

indexes

for the

objects constitute the membership

evaluation matrix which is expressed by

COMPREHENSIVE EVALUATION OF THE RAILWAY PASSENGER'S SATISFACTION BASED ON ROUGH SET

AND ENTROPY

631

11 12 1

21 22 2

nn nm

rr r













 



(d)

Then we standardize the evaluation matrix

and get the matrix

'()

ij n m





(e)

stands for the membership of the evaluation

indexes.

(2)

Normalize all the indexes and calculate the

indicator values of the

evaluation objects for

the

indexes.





(f)

(3)

Calculate the entropy of the index

Given

1/lnKn

(0,0 1)

Kp

and

ln 0

ij ij

pp

p 

. The entropy formula is:

ln ( 1, 2, )

jijij

HKppj n



 





(g)

(4)

Calculate the coefficient of variation of index





(h)

(5)

Calculate the weight of the index







(i)

5 COMPREHENSIVE WEIGHT

If the subject weight to index

and the

object weight is

, the comprehensive weight

formula (Wu Chun-you, Liu Yan, 2010; Hong Zhang,

Chao-lin Gu, Lu-wen Gu, Yan Zhang, 2011) to the

index

is as follows.

ioi











(j)

6 EMPIRICAL STUDY

In this paper, we choose Ticket Price,

Convenience,

Train speed,

Comfort and Security as the indicators

to assess the passenger’s satisfaction. We analysis

the 1051 questionnaires surveyed in January in the

year 2010 and calculate the subject weight and

object weight of the five indexes by the rough set

theory and the Entropy theory. Finally we obtain the

comprehensive weight of the five indexes by using

the comprehensive weight formula.

6.1 Subject Weight based on Rough Set

According to the rough set theory, the 1051

questionnaires surveyed constitute the set of the

objects. That is





1 2 1051

,,Uxx x 

. The evaluation

of the passenger to the five indexes Ticket Price,

Convenience, Train speed, Comfort and Security

constitute the set of the condition attributes. That is





12345

,,,,C ccccc

. In this set, the sign

stands

for the index of Ticket Price. The sign

stands for

the index of Convenience. The sign

stands for

the index of Train speed. The sign

stands for the

index of Comfort. The sign

stands for the index

of Security. The overall satisfaction evaluation

constitutes the decision attribute which is expressed

There are seven evaluation grades for each index.

For example, for the index Ticket Price, the seven

evaluation grades are extremely dissatisfied, very

dissatisfied, slightly dissatisfied, general, slightly

satisfied, very satisfied and extremely satisfied. The

satisfaction degree of the seven evaluation grades

deepens gradually. We use the numbers 1, 2, 3, 4, 5,

6 and 7 to stand for the seven evaluation grades

correspondingly. For instance, 1stands for extremely

dissatisfied, 2 stands for very dissatisfied and so on.

The other indexes such as Convenience,

Train speed,

Comfort, Security and the overall satisfaction

evaluation have the same evaluation grades and

expression in numbers. The evaluation scores are

shown in

Table 1.

According to the weight calculation formula in

the rough set theory, we use the ” Matlab” software

to program the appropriate procedures and get the

correspondingly evaluation results as follows. The

and

stand for the

subjective weight of Ticket Price,

Convenience,

Train speed, Comfort and Security correspondingly.

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

632

Table 1: Passenger satisfaction evaluation score sheet.

Data

Condition Attribute

Decision

Attribute

2 4 4 4 5 4

3 5 2 4 5 5

      

1051

2 4 2 3 5 3

Note: the dates come from the survey questionnaire in

January in 2010.





( ) 446

Card pos D 

( ) 219

Card pos D











()

227

() 1

() 446

Card pos D

Sig c

Card pos D







 

() 196

Card pos D











()

250

()1

( ) 446

Card pos D

Sig c

Card pos D







 

() 186

Card pos D











()

260

()1

( ) 446

Card pos D

Sig c

Card pos D







 

( ) 234

Card pos D











()

212

()1

() 446

Card pos D

Sig c

Card pos D







 

() 181

Card pos D











()

265

()1

( ) 446

Card pos D

Sig c

Card pos D







 

()

227

0.186985,

1214

()

Cc k

Sig c









()

250

0.205931,

1214

()

Cc k

Sig c









()

260

0.214168,

1214

()

Cc k

Sig c









()

265

0.174629,

1214

()

Cc k

Sig c









()

265

0.218287,

1214

()

Cc k

Sig c









According to the results above we get the

subjective weight of the five indexes using the rough

set theory. The subjective weight of the Ticket Price

is 0.186985. The subjective weight of the

Convenience is 0.205931.The subjective weight of

the Train speed is 0.214168. The subjective weight

of the Comfort is 0.174629. The subjective weight of

the Security is 0.218287. The weight of the Security

is the highest in all the five weights. And then is the

weight of the Train speed and the weight of

Convenience. So in the subjective aspects the

passengers pay the most attention on their security in

the travel because the security is the premise of

human existence. Besides, with the development of

the society, people are increasingly concerning more

about the time value which is affect a lot by the

Train speed and the Convenience in their travel. So

the results show that the weights of the Train speed

and Convenience are a little higher than the weights

of Ticket Price and Comfort subjectively.

6.2 Objective Weight based

on Entropy

Different evaluation grades of each index has

different number of people. We process the data and

calculate the number of people in different

evaluation grades. the distribution results are listed

below in Table 2.

COMPREHENSIVE EVALUATION OF THE RAILWAY PASSENGER'S SATISFACTION BASED ON ROUGH SET

AND ENTROPY

633

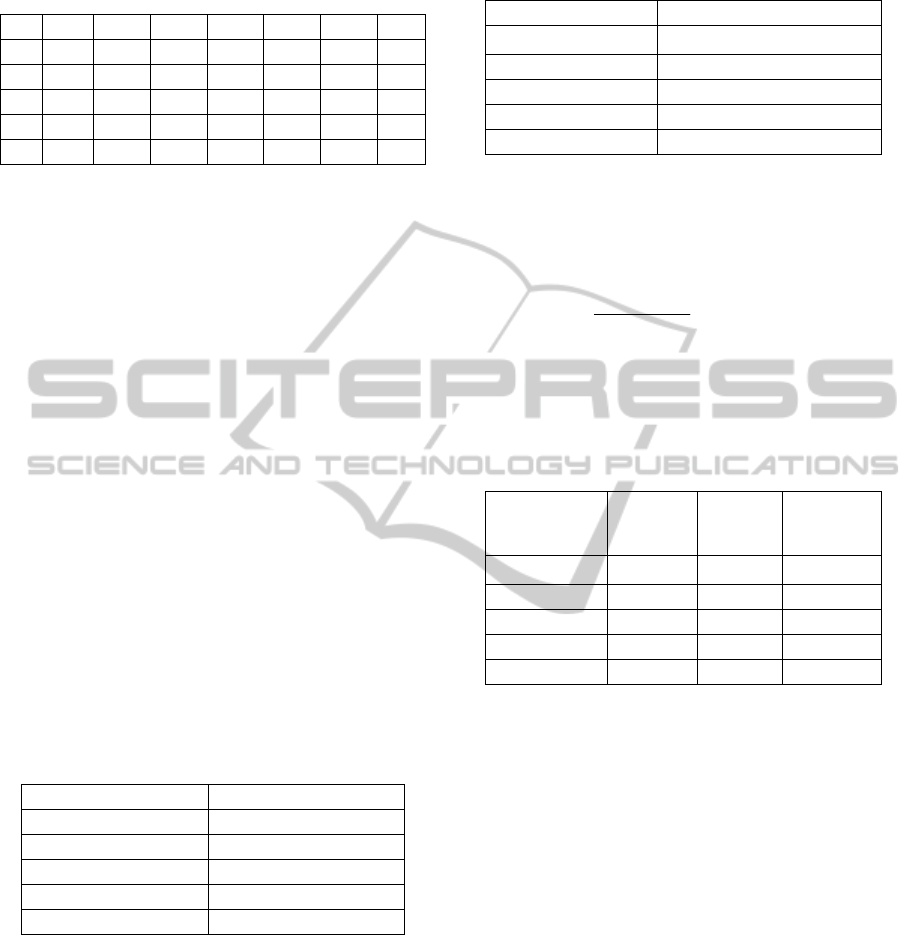
Table 2: Distribution tables of different people in different

evaluation grades.

D1 D2 D3 D4 D5 D6 D7

I1 4 19 203 404 349 69 3

I2 21 62 151 378 315 87 37

I3 55 108 204 293 266 88 37

I4 33 69 197 363 256 104 29

I5 2 5 36 141 520 277 70

The

I1, I2, I3, I4 and I5 stand for the Ticket

Price, Convenience, Train Speed, Comfort

and

Security

correspondingly.

We Standardize and normalize the membership

matrix composed of the evaluation form in Table

2.Then we calculate the Distribution matrix of

different people. The result is as follows.

0.0038 0.0200 0.0523 0.0314 0.0019

0.0181 0.0590 0.1028 0.0657 0.0048

0.1931 0.1437 0.1941 0.1874 0.0343

( ) 0.3844 0.3597 0.2788 0.3454 0.1342

0.3321 0.2997 0



 .

.2531 0.2436 0.4948

0.0657 0.0828 0.0837 0.0990 0.2636

0.0029 0.0352 0.0352 0.0276 0.0666







According to the entropy formula:

ln ( 1, 2, ).

jijij

HKppj n



 





We calculate the entropy of each index in

Table 3.

Table 3: Entropy of each index.

Entropy

()

Ticket Price

()

0.2838

Convenience

()

0.173

Train Speed

()

0.0985

Comfort

()

0.1432

Security

()

0.3016

According to the formula of the coefficient of

variation, we get the final objective weight of each

index. The results are as follows in Table 4.

Table 4: Objective weight of each index.

Objective Weight

()

Ticket Price

()c

0.2838

Convenience

()

0.173

Train Speed

()

0.0985

Comfort

()

0.1432

Security

()

0.3016

6.3 Calculate the Comprehensive

Weight

Finally, according to the comprehensive weight

formula:

si oi

ioi











We get the comprehensive weight of each index

in Table 5.

Table 5: Comprehensive weight of each index.

Subject

()

Object

()

Complex

()

Ticket Price

0.186985 0.2838 0.2645

Convenience 0.205931 0.173 0.1776

Train Speed 0.214168 0.0985 0.1052

Comfort 0.174629 0.1432 0.1246

Security 0.218287 0.3016 0.3282

7 CONCLUSIONS

The result of the objective weight calculated by the

entropy theory is that the weight of the Security is

the highest which is the same to the subjective

weight of Security calculated by the rough set theory.

That is to say all the people consider their personal

security as the most important part in their travel, no

matter subjectively or objectively. Besides,

passengers pay more attention on the Train Speed

and Convenience than the Ticket Price and the

Comfort subjectively. But objectively passengers

usually think the Ticket Price and Convenience are

more important than the Comfort and the Train

Speed. In general, the results of the comprehensive

weights show that the passengers pay the most

attention on Security. The followed indexes are the

Ticket Price and the Convenience. The Comfort and

Train Speed are not important enough to arouse too

ICEIS 2011 - 13th International Conference on Enterprise Information Systems

634

much attention of passengers in their travel generally.

So based on this result the railway department

should try their best to ensure the passengers’

personal and property safety. They should improve

the safety of train operation and reduce the accident

rate so that they can more passenger flows.

Moreover, the railway department should make more

appropriate strategies which are more diversified

and flexible to provide the passengers more choice

in the ticket price make them feel more satisfied.

What’s more, the railway department should

improve the convenience of the passenger transfer

between the railway and the other ways so that they

can reduce the passengers’ transfer times and lower

their burden. At last we should provide a more

comfortable environment and raise the travel speed

reasonably to give the passengers a more convenient

and comfortable service.

REFERENCES

Wu Chun-you, Liu Yan, 2010. Urban renewable resources

stakeholders satisfaction evaluation model and

empirical research. China’s population - Environment

and Resources. 20 (30). 117-123.

Ma Xiao-ying, Zhang Guo-hai, Han Shu-fen, 2007.5. The

university library reader’s comprehensive fuzzy

satisfaction evaluation based on the entropy.

Information science. 25 (25). 715-719.

Song Li-min, 2009.4. Reader’s comprehensive fuzzy

satisfaction evaluation based on the AHP and entropy

method. Modern information. 29(4). 58-61.

Meng Ming, Niu Xiao-dong, Gu Zhi-hong, 2005.7. Power

customer’s satisfaction evaluation model based on the

fuzzy entropy theory. Journal of North China Electric

Power University. 32 (4). 68-70.

Peng Jin-shuan, Hao Yi-ming, Peng Li-fang, 2007. The

public transportation fuzzy comprehensive satisfaction

evaluation based on the entropy theory. Shan Xi

Construction.

Xiong Ping, Cheng Hua-bin, Wu Xiao-ping, 2003. A

comprehensive weighting method based on the rough

set theory. Journal of Naval University of Engineering.

Hao Cheng, Li Jing, Li Xue-Mei, Li Xue-wei, 2008. The

research of the weight of the effectiveness factors in

the urban rail transit project based on the rough set. 29

(6). 121-125.

Liu Jie, Li Chao-feng, Li Xiao-peng, Wen Bang-chun,

2008. Product generalized quality evaluation and

application based on matter element and the combined

weights. Journal of Northeastern University (Natural

Science Edition). 29 (9). 1314-1317.

China Research Center of Industrial Safety in Beijing

Jiaotong University, 2009.Report of China Financial

Industry Security in 2009. Publisher of Beijing

Jiaotong University. 138-148.

Chun-bao Chen, Li-ya Wang, 2006. Rough Set-Based

Clustering with Refinement Using Shannon’s Entropy

Theory.Computers and Mathematics with Applications.

1563-1576.

Don-Lin Mon, Ching-Hsue Cheng, Jiann-Chern Lin, 1994.

Evaluating weapon system using fuzzy analytic

hierarchy process based onentropy weight. Fuzzy Sets

and Systems.127-134.

Hong Zhang, Chao-lin Gu, Lu-wen Gu, Yan Zhang, 2011.

The evaluation of tourism destination competitiveness

by TOPSIS & information entropy —A case in the

Yangtze River Delta of China. Tourism Management.

APPENDIX

This paper was supported by “National Science and

Technology Support Projects (2009BAG12A10-1)”

and “Railway Ministry Projects (2010Z012)”.

COMPREHENSIVE EVALUATION OF THE RAILWAY PASSENGER'S SATISFACTION BASED ON ROUGH SET

AND ENTROPY

635