NURSE SCHEDULING BY COOPERATIVE GA WITH PENALTY

COEFFICIENT ADJUSTMENT

Makoto Ohki and Hideaki Kinjo

Division of Information and Electronics, Graduate School of Tottori University

101, 4 Koyama Minami, Tottori, 680-8552 Japan

Keywords:

Nurse scheduling, Genecit algorithm, Cooperative genecitic algorithm, Penalty coefﬁcient adjustment.

Abstract:

This paper describes a penalty adjustment technique for CGA applied to the nurse scheduling problem. The

nurse scheduling is very complex task, because many requirements must be considered. In real hospital, some

changes of the schedule often happen. Such a change of the shift schedule yields various inconveniences.

Such an inconvenience causes the fall of the nursing level of the whole nurse organization. Furthermore,

reoptimization of the schedule including such changes is very hard task and requires very long computing

time. To improve this problem, we propose a technique to adjust penalty coefﬁcient through the optimization.

1 INTRODUCTION

General hospitals consist of several sections such as

the internal medicine department and the pediatrics

department. Each section is arranged by the nursing

staff of about ﬁfty to thirty. A section manager makes

a roster, or a shift schedule, of all nurses in her/his

section every month. The manager considers more

than ﬁfteen requirements for the scheduling. Such

the schedule arrangement, in other words, the nurse

scheduling, is very complex task. Therefore, com-

puter software for the nurse scheduling has recently

come to be strongly required.

The shift schedule generated by such the com-

mercial software is unsatisfactory. In fact, the nurse

schedule is still made by the hand of the manager in

many general hospitals. The optimization algorithm

of such the commercial software is still poor. We

discuss on generation and optimization of the nurse

schedule by using the Cooperative Genetic Algorithm

(CGA) (T. Itoga, 2003). CGA is a kind of Genetic Al-

gorithm (GA) (D. E. Goldberg, 1989), and powerful

optimizing algorithm for such a combinatorial opti-

mization problem.

Burke et al. (E. K. Burke, 2001) have proposed

a technique to evaluate the nurse schedule. How-

ever, this technique does not ﬁt to the shift system

of our country. Therefore, we have to deﬁne the

evaluation technique of the nurse schedule. In the

real case, there are some cases that nurses attend

on a different day from the original schedule. We

have discussed such a case that the schedule has been

changed in the past weeks(M. Ohki, 2007; S. Uneme,

2008). The changed schedule must be reoptimized to

avoid various inconveniences. Such an inconvenience

causes the fall of the nursing level. Reoptimization of

the schedule including such the changes is very hard

task even by parallel computing techniques (M. Ohki,

2010b; M. Ohki, 2010a). We consider that this com-

plexity is caused by that there are many local minima

in the solution space of the nurse scheduling prob-

lem. We propose a technique adjusting penalty coef-

ﬁcient through the optimization when the concerned

penalty function stagnate decreasing. If the optimiza-

tion is caught in the region of the local minimum,

some penalty functions stagnate decreasing. Valley

of the local minimum upheaves by increasing weight

of such the penalty function. And then, the search-

ing point of the optimization escapes from the local

minimum region.

2 NURSE SCHEDULING BY CGA

In the nurse scheduling by CGA, an individual and

a population, are deﬁned as shown in Fig.1. The in-

dividual consists of the series of the shift symbols.

The shift series consists of 28 ﬁelds, where it means

four weeks. The i-th individual expresses one-month

schedule of the i-th nurse. In CGA, each individual

denotes the schedule of each nurse. The population

255

Ohki M. and Kinjo H..

NURSE SCHEDULING BY COOPERATIVE GA WITH PENALTY COEFFICIENT ADJUSTMENT.

DOI: 10.5220/0003618902550258

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 255-258

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

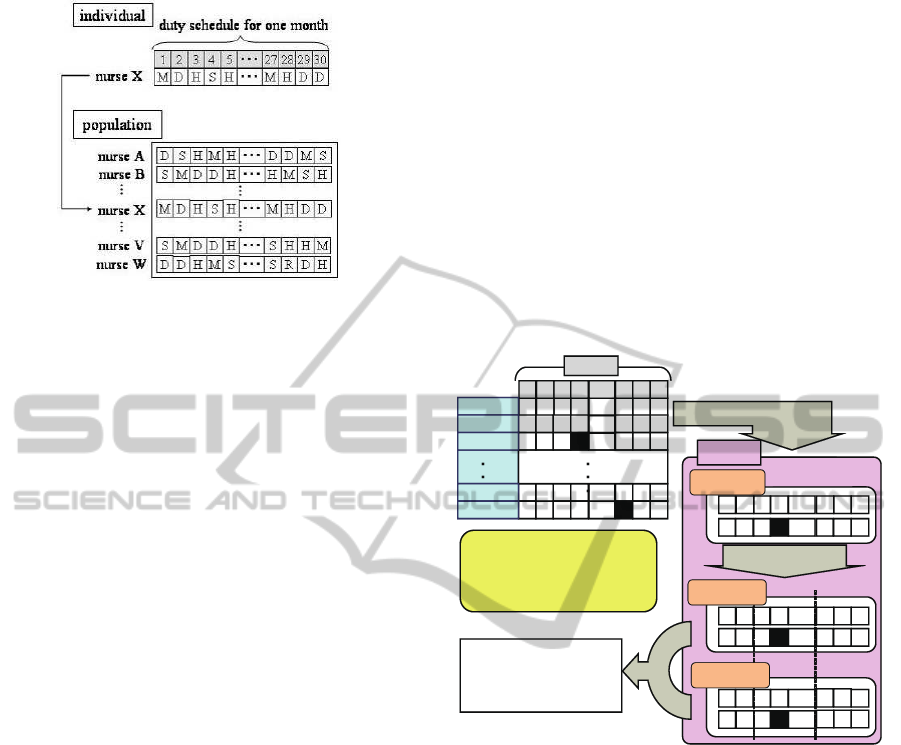
Figure 1: The individual and the population.

denotes one-month schedule.

We have summarized all the requirements into the

13 penalty functions to evaluate the population. De-

tail of these penalties has been shown in the previous

research work (M. Ohki, 2010a). We describe an out-

line of each penalty.

The following penalty functions evaluate work

load of each nurse. A penalty function F

evalutates

the work loard of each nurse i for three consecutive

days. A penalty function F

evaluates to prohibit the

X night shift or more for the consecutive Y days. A

penalty function F

evaluates speciﬁc prohibited shift

pattern.

The following penalty functions evalute the num-

ber of the shifts impartially assigned. Penalty func-

tions F

, F

supress unevenness of the number of

shifts among nurses on the holidays and the night

shifts. A penalty function F

restrains assignment of

the shift on many consecutive shift days.

In our CGA, the number of nurses in each work-

ing hours is preserved in any case. We deﬁne penalty

functions F

, F

and F

to evaluate the nursing level

on the day time shift, the semi-night shift and the mid-

night shift respectively.

The following penalty functions evaluate about

the combination of the nurses. A penalty function F

10j

restrains unfavorable afﬁnity of nurses. A penalty

function F

11j

restrains unfavorable situation that too

many new faces are assigned on the midnight shift. A

penalty function F

12j

restrains unfavorable situation

that one or more expert or more skilled nurses are not

assigned to the daytime shift and the midnight shift.

A penalty function F

performs the difference be-

tween the original schedule and the newly optimized

schedule of the remainder of the current month to

restrain the falls of the nursing level because of the

change of the schedule.

Finaly, we perform the shift schedule by the fol-

lowing total penalty function at g-th generation,

E(g) =

∑

+ h

)

∑

+ h

)

∑

+ h

)

∑

10j

+ h

11j

+ h

12j

) + h

, (1)

where h

—h

denote penalty coefﬁcients.

The basic algorithm of the CGA is as shown in

Fig.2 (M. Ohki, 2006; M. Ohki, 2007; S. Uneme,

2008). CGA applies the crossoveroperator to the pop-

ulation and searches so that a penalty of the whole

population becomes small.

D S

S M

1 2

3 4

nurse A

nurse B

D D

D M S

M S

26 27 28

h M

䊶䊶䊶

M h D Hnurse C

S h

䊶䊶䊶

nurse Y

nurse Z

date

D S h M D M S

䊶䊶䊶

M h D H

S h

䊶䊶䊶

crossover

D S

M D M S

䊶䊶䊶

M h

S h

䊶䊶䊶

D S

h M

D M S

䊶䊶䊶

M h

D H

S h

䊶䊶䊶

two-point crossover

Each pair is taken back to

the original position of

their parents and whole

population is performed.

select two individuals

parent pair

child pair 1

child pair 2

This procedure is repeated for

100 parent pairs. One pair

giving best performance is

selected for the next generation.

Figure 2: One generation cycle by the crossover operator.

When the optimization stagnates for long genera-

tion cycles, it is effectiveto forcibly give small change

to the population. Therefore we have proposed a mu-

tation operator activated depending on the optimiza-

tion speed V

(g). When V

becomes less than or

equeal to a speedo-thleshold ε

, the mutation is ac-

tivated. We have deﬁned two parameters, a guard

interval G

to prevent the activation of the mutation

operator for G

generation cycles right after the last

activation.

We also have proposed a periodic mutation opera-

tor activated periodically in G

generation cycles(M.

Ohki, 2010b). This mutation is advantage on the point

that fewer parameter is required to deﬁne itself.

3 PENALTY ADJUSTMENT

The shape of the solution space is deﬁned by the pen-

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

256

alty function E(g). By changing the penalty coefﬁ-

cients, the shape of the solution space is also changed.

Valley of the local minimum upheaves by increasing

weight of such the penalty function. And then, the

searching point of the optimization escapes from the

local minimum region. The optimization ﬂow with

Penalty coefﬁcient Adjustment (PA) is as shown in

Figure 3.

START

mutation

operator

crossover operator

initialize

END

?0%

=∨< Ggv

)13,,2,1(1:

,0:,

L==

=++

g ,

Figure 3: Optimization ﬂow with the penalty adjustment.

First, all the penalty coefﬁcients h

—h

are ini-

tialized to 1. The decreasing speed of each penalty

function at the generation cycle g, V

(g), is calculated

in PA by the following equations,

(g) =











−1

∑

h=0

∑

i=1

(g− h) (k ≤ 6),

−1

∑

h=0

∑

j=1

(g− h) (k > 6),

(2)

(g) = A

(g− 1) − A

(g). (3)

As shown in Figure 4, when the decreasing speed of

the k-th penalty function, V

, becomes less than or

equal to a speed threshold ε

, the penalty coefﬁcient

is increased by multiplying with parameter α. In

this research, the values of ε

and α are deﬁned as

0.01 and 1.01 respectively. When the mutation is ac-

tivated, all the penalty coefﬁcients h

—h

are initial-

ized to 1 again.

4 PRACTICAL EXPERIMENT

We have tried computational experiment of the nurse

scheduling with practical data. In order to compare

exactly, we have tried to optimize the ten times un-

der each condition. Figures 5 (a)—(c) show examples

13 penalty coefficients

tv ε≤)(

: hh ⋅= α

tv ε≤)(

1313

: hh ⋅= α

tv ε≤)(

: hh ⋅= α

Figure 4: Primitive operation of the penalty coefﬁcient ad-

justment.

of the variation of the penalty coefﬁcients modiﬁed

by PA. In the initinal stage of the optimization, sev-

eral coefﬁcients are increased extremely. While the

optimization progresses, the penalty coefﬁcients wig-

gle for long term of the generation cycle. In these

generation cycles, the mutation is activated in a short

period. In other words, the optimization stagnates fre-

quently. This means that the optimization is caught

in the local minimum region. Approaching the end of

the optimization, we can ﬁnd several generation inter-

vals which the mutation is not activatedand then some

of coefﬁcients are increased extremely. In these inter-

vals, the optimization progresses for a long generation

interval. In the ﬁnal stage of the optimization, the pro-

gression of the optimization clearly represented. This

suggests that the optimization goes towards conver-

gence.

Figure 6 shows optimization progress by using the

periodic mutation operator and PA respectively. The

red dotted lines and blue solid lines denote maximum,

average and minimum value of the penalty function E

given by the periodic mutation and PA respectively. In

one trial, the optimization is executed for N

= 500

mutation cycles. By means of PA, the optimization

ﬁnishes in about one-tenth generation cycles by the

periodic mutation.

Figure 7 shows comparison of the maximum, the

average and the minimum value of the ten results un-

der each technique. Compared to the periodic muta-

tion operator, PA is slightly worse. Both results are,

however, within the range between 169—174. This

means that both results are almost regarded as satis-

factory.

5 CONCLUSIONS

This paper has shown a technique of nurse scheduling

by using CGA. We have discussed the case that the

nurse schedule has been changed in the past weeks.

To reoptimize the changed schedule, we have de-

NURSE SCHEDULING BY COOPERATIVE GA WITH PENALTY COEFFICIENT ADJUSTMENT

257

100

1000

10000

100000

1000000

10000000

100000000

0 2000 4000 6000 8000 10000

penalty coefficient

generation cycle

h10

h11

h12

h13

(a) from 0-th generation to 10000-th generation

100

1000

10000

100000

1000000

10000000

30000 32000 34000 36000 38000 40000

penalty coefficient

generation cycle

h10

h11

h12

(b) from 30000-th generation to 40000-th generation

100

1000

10000

100000

1000000

10000000

penalty coefficient

generation cycle

h10

h11

h12

h13

Figure 5: The variation of the penalty coefﬁcients. Each

vertical axis shows on a logarithmic scale.

165

170

175

180

185

190

0 200000 400000 600000 800000 1000000

penalty E

genera!on cycle g

Figure 6: Comparison of the optimization progress between

CGA with the periodic mutation and CGA with PA.

168

170

172

174

convenonal

Penalty Funcon E

Figure 7: Comparison of the optimization result between

the periodic mutation and PA.

ﬁned a penalty function performing the difference be-

tween the original schedule and the optimizing sched-

ule. Therefore we need new techniques to search for

good schedule effectively. We have proposed a tech-

nique adjusting the penalty coefﬁcient depending on

the optimization progress, PA. This technique is im-

plemented with the mutation depending on the opti-

mization speed. By means of PA, the optimizationﬁn-

ishes within one-tenth generation cycles by the con-

ventional periodic mutation technique.Thus, the ef-

fectiveness of PA is conﬁrmed.

ACKNOWLEDGEMENTS

This research work has been supported by Tot-

tori University Electronic Display Research Center

(TEDREC).

REFERENCES

D. E. Goldberg (1989). Genetic Algorithm in Search, Opti-

mization and Machine Learning. New York.

E. K. Burke, P.De Causmaecker, S. G. (2001). Fitness eval-

uation for nurse scheduling problems. In Proceedings

of the 2001 Congress on Evolutionary Computation.

M. Ohki (2010a). Effective mutation operator for nurse

scheduling by cooperative ga and its parallel process-

ing. In 19th Int. ACM Workshop on Parallel Architec-

tures and Bioinspired Algorithms, pages 1–8.

M. Ohki, S.Uneme, H. (2010b). Effective mutation operator

and parallel processing for nurse scheduling. In Stud-

ies in Computational Intelligence, volume 299, pages

229–242. DOI: 10.1007/978-3-642-13428-9 10.

M. Ohki, A. Morimoto, K. (2006). Nurse scheduling

by using cooperative ga with efﬁcient mutation and

mountain-climbing operators. In 3rd Int. IEEE Con-

ference Intelligent Systems, pp.164-169.

M. Ohki, S. Uneme, S. M. (2007). Effective genetic

operators of cooperative genetic algorithm for nurse

scheduling. In 4th Int. INSTICC Conference on In-

formatics in Control, Automation and Robotics, pages

347–350.

S. Uneme, H. Kawano, M. (2008). Nurse scheduling by co-

operative ga with variable mutation operator. In Proc.

of 10th ICEIS, INSTICC, pages 249–252.

T. Itoga, N. Taniguchi, Y. K. (2003). An improvement on

search efﬁciency of cooperative ga and application on

nurse scheduling problem. In Proc. of 12th Intelligent

System Symposium, pages 146–149.

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

258