STRUCTURE-BASED INTERROGATION AND AUTOMATIC

QUERY REFORMULATION

Mohamed Ben Aouicha, Ines Kamoun, Mohamed Tmar and Abdelmajid Ben Hamadou

MIRACL, Sfax University, Sfax, Tunisia

Keywords:

XML retrieval, XML query optimization, Virtual link, INEX.

Abstract:

This paper presents an information retrieval model on XML documents based on tree matching. Queries and

documents are represented by extended trees. An extended tree is built starting from the original tree, with

additional weighted virtual links between each node and its indirect descendants allowing to directly reach

each descendant. Therefore only one level separates between each node and its indirect descendants. This

allows to compare the user query and the document with ﬂexibility and with respect to the query structural

hints. The content of each node is however very important to decide whether a document element is relevant or

not, thus the content should be taken into account in the retrieval process. We separate between the structure-

based and the content-based retrieval processes. The structure notion should be taken into account during the

retrieval process as well as during automatic query reformulation. We propose an approach to automatic query

reformulation starting from the original query on one hand and the fragments judged relevant by the user on

the other. Structure hints analysis allows us to identify nodes that match the user query and to rebuild it during

the automatic query reformulation step. The main goal of this paper is to show the impact of structural hints in

XML retrieval and XML query optimization. Some experiments have been undertaken into a dataset provided

by INEX

to show the effectiveness of our proposals.

INitiative for the Evaluation of XML retrieval, an evaluation forum that aims at promoting retrieval capa-

bilities on XML documents.

1 INTRODUCTION

The standardization of the Web to XML schemas

presents new problems and hence new needs for cus-

tomized access to information. Being a very powerful

and often unavoidable tool to customized access to in-

formation of all kinds, information retrieval systems

arise at the forefront of this issue.

Many traditional information retrieval systems

(IRS) have been adapted to handle XML retrieval.

While both text and structure are important, IRS usu-

ally give higher priority to text when ranking XML

elements. IRS adapt unstructured retrieval methods

to handle additional structural constraints. Such ap-

proaches are called text centric XML retrieval.

The traditional information retrieval systems han-

dle documents with different formats but do not ex-

ploit the structure of documents, including the refor-

mulation phase of the query. However, a structured

document is characterized by its content and struc-

ture. This structure, as deﬁned by elements, possibly

completes semantics expressed by the content and be-

comes a constraint with which information retrieval

systems must comply in order to satisfy the user in-

formation needs.

Indeed, the user can express his need by a set of

keywords, as in the traditional information retrieval

systems, and can add structural constraints to better

target the sought semantics.

Thus, taking into account the structure of the doc-

uments and that of the query by the information re-

trieval systems handling structured documents is nec-

essary not only in the retrieval process but also in the

query reformulation one.

We propose in this paper to evaluate the impact

of structure handling in both the interrogation and the

query reformulation process. The structure hints in

the user query are taken into account at ﬁrst (before

any content treatment) in interrogation process, and

in the query reformulation process, the query struc-

ture could be devoted to some modiﬁcation based on

the structure of the relevant judged document frag-

ments. thus, we put the emphasis on the structure by

analyzing the structure features and relation that are

123

Ben Aouicha M., Kamoun I., Tmar M. and Ben Hamadou A..

STRUCTURE-BASED INTERROGATION AND AUTOMATIC QUERY REFORMULATION.

DOI: 10.5220/0003624601230128

In Proceedings of the International Conference on Knowledge Management and Information Sharing (KMIS-2011), pages 123-128

ISBN: 978-989-8425-81-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

the most signiﬁcant to the interrogation and the query

reformulation process.

This paper is organized into six sections. The sec-

ond section gives a survey of related work in XML re-

trieval. The third section presents our XML retrieval

model. In the fourth section, we present an auto-

matic query reformulation approach. The ﬁfth section

presents the experiments and the obtained results. The

sixth section concludes.

2 RELATED WORK IN XML

RETRIEVAL AND AUTOMATIC

XML QUERY

REFORMULATION

In traditional information retrieval (IR), the docu-

mentary unit from which the terms are extracted and

which will be presented to the user is the entire doc-

ument. But in the context of XML retrieval the doc-

umentary unit can have different forms. It can be the

entire document (any element of the document) or an

item or subtree of an XML document. Thus XML

retrieval systems must take into account this new di-

mension during the interrogation of any XML corpus

and during the query reformulation.

Several teams have adapted classical IR methods

to XML retrieval. The vector-space based XML re-

trieval method proposed by deﬁnes each dimension

by sub-trees that contain at least one indexing term.

Queries and documents are then represented by vec-

tors in this space and the system computes matches

between them using well-knownvector-space similar-

ity measures (Cosine, Dice, Overlap . ..). Schlieder

and Meuss (Schlieder and Meuss, 2002) describe

similar approaches. They proposed the ApproXQL

model, which integrates the document structure in the

vector space model similarity measure. The query

model is based on tree matching: it rewrites the

queries and the documents independently and then

performs XML retrieval based on the traditional vec-

tor space model properties.

Fuhr (Fuhr and Grossjohann, 2001) uses a query

language XIRQL that combines the structural and the

content based approach. It integrates features related

to data-centric by using ideas from logic-based prob-

abilistic Information retrieval models, in combination

with concepts from the database area. Balog et al.

propose a general probabilistic framework for entity

search to evaluate and provide insight in the many

ways of using these types of input for query modelling

(Balog et al., 2010). They focus on the use of cate-

gory information and demonstrates the effectiveness

of category-based expansion using example entities.

3 OUR XML RETRIEVAL MODEL

We present in this section an XML retrieval model

based on tree ﬂexible matching. Instead of ﬂexible

matching on the original representations of the query

and the document, we apply an exact match method

on ﬂexible representations of them.

Formally, an XML tree is a set of node paths A −→

B where node A is the parent of node B. The XML

tree root is the only one that has no parent. So an

XML tree T should have the following property:

{N,∀N

′

−→ N /∈ T} = {root} (1)

where N and N

′

represent XML nodes in tree T.

A fragment can be deﬁned by the result of the in-

ner join of two paths. For example, if an XML tree

contains paths A −→ B and B −→ C, we can deﬁne an-

other path A −→ B −→ C. A path is then an ordered

list of nodes N

−→ N

−→ ... −→ N

. No cycles

have to occur in a tree path, thus if N

−→ N

−→

... −→ N

is a path resulted from the tree T, all N

should be different. This brings to another property

which requires that each node but the root has only

one parent:

∀N,|{N

′

−→ N ∈ T}| =



0 if N = root

1 otherwise

(2)

An XML tree is then a set of paths that fulﬁlls the

properties 1 and 2.

The structure retrieval can be viewed as compar-

ing between the structures of two XML trees. Com-

paring between trees was initially introduced by the

tree to tree correction theory (Selkow, 1977). To com-

pare between two trees, we have a tendency to build

a tree starting from the second tree and then com-

pute correction costs. The correction process consid-

ers hidden relations between nodes. For example, if

node A is the parent of node B which is the parent of

node C in the tree T, and node A is the parent of node

C in the tree T

′

, the T to T

′

correction can be held

by removing node B and linking node A with node C.

Each update operation has a cost and the tree to tree

correction cost (the edit distance) is the total cumu-

lated cost of the necessary correction operations. The

total cost c of tree to tree correction can be viewed

as the inverse of the similarity between both of them.

Typically, if c = 0, this means that no correction oper-

ation is needed to build a tree starting from the other,

so they are quite similar.

This process can be applied to estimate the struc-

ture similarity between two XML documents, or an

KMIS 2011 - International Conference on Knowledge Management and Information Sharing

124

XML document and an XML query. The main mo-

tivation of its application is that it allows to perform

structure comparison, which is necessary in XML re-

trieval and second, it provides a ranked list of docu-

ment trees (or document sub-trees), where the score

is the inverse of the total cumulated cost of the doc-

ument tree to the query tree correction (or the query

tree to the document tree correction). However, due to

some practice reasons, this cannot be applied to XML

retrieval. The tree to tree correction algorithms are not

scalable: they cannot be applied on XML retrieval on

very large corpuses.

The structural retrieval process should look for the

deepest and widest sub-tree shared by both represen-

tations (Selkow, 1977). Instead of applying a tree to

tree ﬂexible correction algorithm in the original trees,

we use a dual process: an exact match algorithm in

ﬂexible representations of each tree. A ﬂexible repre-

sentation of an XML tree explores all hidden relations

that could exist between nodes. We call such repre-

sentation the extended tree. This operation is done

since indexing the XML corpus.

To do so, we add to each path A −→ B a weight re-

ﬂecting the importance of the relation between nodes

A and B. According to the parent-child relation, this

weight is equal to 1. The more A is distant from B

in the original path, the less its weight is. The weight

depends on the distance between two nodes that occur

in a path. We use the weighting function f deﬁned by

f(A −→ B) = exp(1 − d(A,B)) where d(A,B) is the

distance that separates node A from node B. We de-

note this path by A

−→ B where w = exp(1− d(A,B))

is the weight of the path A −→ B.

We apply an exact match algorithm on the ex-

tended trees (Ben Aouicha et al., 2006) (Ben Aouicha

et al., 2009). As the complexity of the exact match al-

gorithms is less than the approximative matching al-

gorithm one, we use this kind of algorithms to com-

pare between two ﬂexible representations. All the

complexity is then moved at the representation phase,

which corresponds to the indexing process. This

phase is only performed once, and the interrogation

process is in contrast performed by the application

of an exact match algorithm on the extended trees

representations which are stored in the index. Start-

ing from tree T and tree T

′

this algorithm looks for

the deepest and widest sub-tree shared by T and T

′

and computes the similarity depending on the weights

of paths appearing in each one. Relevant fragments

are those having similar structure than the user query.

This can be done by looking in the extended docu-

ment for fragments having exactly the same structure

as the extended query or a part of it. This allows ﬂex-

ible XML retrieval (Bordogna and Pasi, 2000). The

search strategy we adopt is iterative. We start from

the extended document and query trees. We build a

returned fragment incrementally, starting from poten-

tially common roots, we build for each one its com-

mon child nodes, and then for each child node, we

build its common child nodes and so on until leaf

nodes. When building relevant candidate fragments,

we compute the structure-based score by cumulating

the product of the paths weights in the document and

their matched ones in the query tree.

The ﬁnal score is a linear combination of the

structure-based score r

and the content-based score

r( f

, f

) = α × r

+ (1 − α) × r

(3)

where α is a parameter that emphasizes the re-

trieval process on the structure constraints or the key-

words. For our experiments, we use α = 0.6.

4 AUTOMATIC QUERY

REFORMULATION

In our approach we focus on the structure of the orig-

inal query and that of document fragments deemed

relevant to the user structure hints. Indeed, this study

allows us to reinforce the importance of these struc-

tures in the reformulated query to better identify the

most relevant fragments to the user’s needs. The anal-

ysis of structures allows us to identify the most rele-

vant nodes and the involved relationships.

4.1 Line of Descent Matrix

According to most approaches to automatic query re-

formulation, the query construction is done by build-

ing a representative structure of relevant objects and

another structure for irrelevant ones, and then build a

representation close to the ﬁrst and farther from the

second.

For example, the Rocchio’s method (Rocchio,

1971) considers a representative structure of a doc-

ument set by their centroid. A linear combination of

the original query and the centroids of the relevant

documents and irrelevant ones can be assumed as a

potentially suitable user need.

We propose to traduce the documents and the

query in a matrix format instead of a wighted term

vector like in Rocchio’s method which is more suit-

able for ﬂat document. We build for each document

a matrix called line of descent matrix (LDM), which

must show all existing ties of kindship between differ-

ent nodes. This representation should also reﬂect the

STRUCTURE-BASED INTERROGATION AND AUTOMATIC QUERY REFORMULATION

125

positions of the various nodes in the fragments as they

are also important in the query reformulation. For an

XML tree (or subtree) A, we associate the matrix de-

ﬁned by M

[n,n

′

] =



P if n → n

′

∈ A(n is the parent of n’)

0 otherwise

Where P is a constant value which represents the

weight of the descent relationship.

As for us, we represent each of the relevant frag-

ments and the initial query in the LDM form. The

value of the constant P for the query LDM construc-

tion is greater than that used for the construction of

other LDMs (which represent the relevant fragments)

to strengthen the weight of the initial query edges fol-

lowing the principle used in the Rocchio’s method

which uses reformulation parameters having different

effects (1 for the initial query, α for the relevant doc-

uments centroid and β for the non relevant documents

centroid where 0 ≤ α ≤ 1 and −1 ≤ β ≤ 0). Note that

no complexity analysis is here needed because of the

low number of relevant judged documents comparing

to the corpus size. In our experiments, we undertake

the query reformulation in a pseudo-feedback way on

the top 20 ranked documents resulting from the ﬁrst

round retrieval. In the other hand, the total number of

tags is over 160 in all the collection and about 5 in a

single fragment, so the matrix size can not exceed 25.

In a fragment can be returned even if the structural

conditions of the query are not entirely fulﬁlled. This

means that if a fragment of an XML document is sim-

ilar but not identical to the query, it can be returned.

The information retrieval systems now has to query

with tolerated differences (a few missing elements or

more additional ones) between the query structure and

the document. Consequently, we believe that the most

effective way to bring this tolerance is to assure that

one element is not only connected to its child nodes,

but to all of its direct and indirect descendants. A re-

lationship between nodes in the same line of descent

is weighted by their distance in the XML tree.

We propose the TC function which is a transitive

closure on the weights of the nodes edges with a com-

mon ancestor. The resulted value will be added to the

weight of the edge itself in the LDM as follows:

∀(n,n

′

′′

) ∈ N

[n,n

′′

] ← M

[n,n

′′

]

+TC(M

[n,n

′

],M

′

′′

])

With:

TC(x,y) =

x× y

+ y

As for us, this transitive closure will be applied to

each LDM of each fragment judjed as relevant and

also to the LDM of the query.

The the reformulated query structure is built start-

ing from the obtained LDMs. Let us consider F =

{ f

, f

.. . f

} where f

are the relevant judged frag-

ments and Q

is the initial query, the query structure

is built starting from the cumulated LDM S:

∀(n,n

′

)

∈ B

,S[n,n

′

] =

∑

f∈F

[n,n

′

] + M

[n,n

′

]

4.2 Building the New Query Structure

The query reformulation starts by identifying its root.

The root is characterized by a high number of child

nodes and a negligible number of parents. For exam-

ple, to ﬁnd the root we simply return the element R,

which has the greatest weight in the rows of the ma-

trix S and the lowest weight in its columns. The root

R is then such that:

R = argmax

n∈B

∑

′

∈B

S[n, n

′

].log







∑

′

∈B

S[n

′

,n]

∑

′

′′

)∈B

S[n

′

′′

]

+ 1







The argument to maximize reﬂects that the can-

didate nodes to represent the root should have as

maximal low values as possible in the relative row

(

∑

n∈B

S[n, n

′

]) and as minimal low values as possible in

the column (

∑

′

∈B

S[n

′

,n]) relatively to the total sum of

the matrix values (

∑

′

′′

)∈B

S[n

′

′′

]).

Once the root has been established, we proceed to

the recursive development phase of the tree represent-

ing the structure of the new query. The development

of the tree starts by the root R, and then by determin-

ing all the child nodes of R, the same operation is

performed recursively for the child nodes of R until

reaching the leaves elements.

5 EXPERIMENTS AND RESULTS

Experiments have been undertaken into a dataset pro-

vided by INEX. The INEX metric for evaluation is

based on the exhaustivity and speciﬁcity measures

which are analogous to the traditional recall and pre-

cision measures (Piwowarski and Dupret, 2006). The

speciﬁcity is an extent to which a document compo-

nent is focused on the information need, while being

an informativeunit. The exhaustivenessis an extent to

KMIS 2011 - International Conference on Knowledge Management and Information Sharing

126

which the information contained in a document com-

ponent satisﬁes the information need. Each document

component has one of the following values of exhaus-

tivity (non exhaustive, slightly exhaustive, exhaustive

very exhaustive) and speciﬁcity (between 0 and 1).

These measures are quantized onto a single relevance

value.

First experiments were undertaken to show the ef-

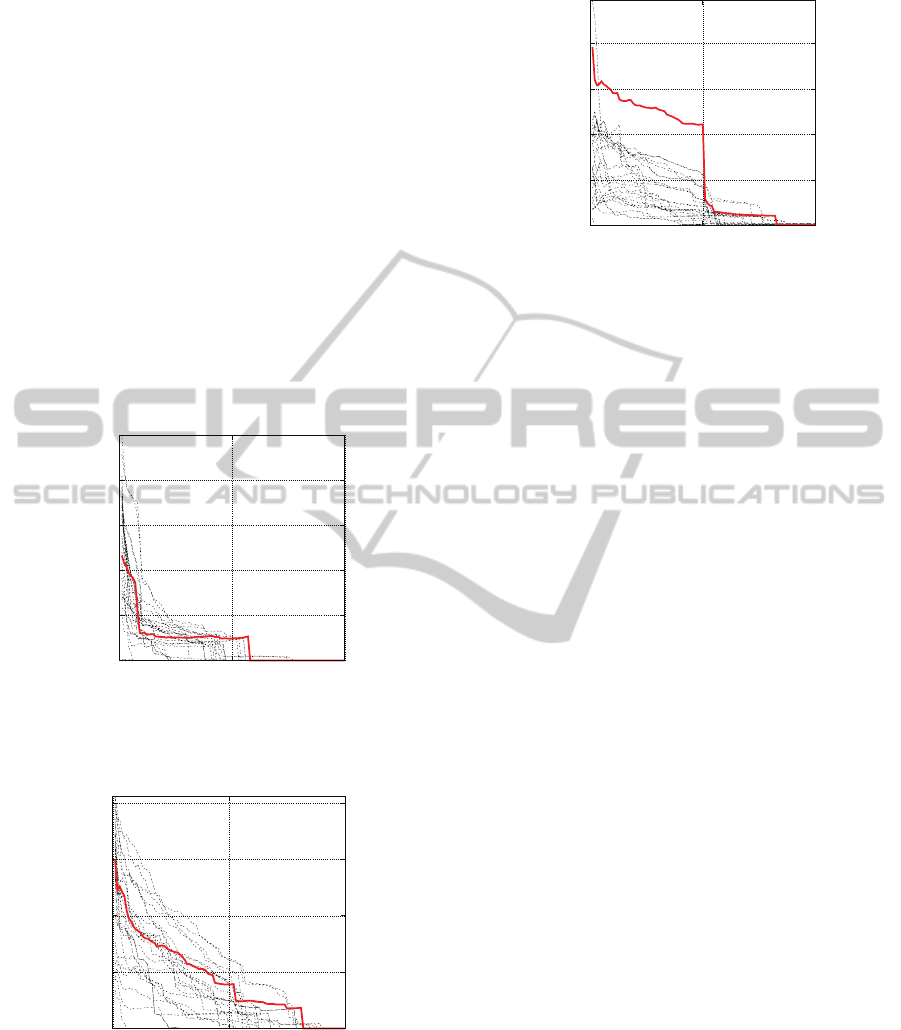
fectiveness of our XML retrieval approach. Figures

1, 2 and 3 show our results (bold curves) compared to

ofﬁcial INEX obtained results by all participants on

the MAep (mean average effort precision) quantiza-

tion measure.

We experimented different values of α used in equa-

tion 3, the value that provides the best results is 0.6

which shows that the strcture-based retrieval contri-

bution is over 40% of the whole XML retrieval pro-

cess.

0.08

0.16

0.24

0.32

0.4

0 0.5 1

effort-precision

gain-recall

Figure 1: Comparative results with INEX ofﬁcial partici-

pants, generalized quantization function.

0.1

0.2

0.3

0.4

0 0.5 1

effort-precision

gain-recall

Figure 2: Comparative results with INEX ofﬁcial partici-

pants, generalized lifted quantization function.

It can be seen through ﬁgure 3 that we obtain

better MAep results than all the INEX’2005 partic-

ipants in the strict quantization functions. Figure 1

and 2 show that our system is very competitive to the

0.07

0.14

0.21

0.28

0 0.5 1

effort-precision

gain-recall

Figure 3: Comparative results with INEX ofﬁcial partici-

pants, strict quantization function.

INEX’2005 outsiders according to the other quantiza-

tion functions.

At the other measures, the results are much closed

to the best INEX’2005 ofﬁcial results.

The obtained results on the strict quantization

function over all measures show that our approach

is able to return high speciﬁc elements to the INEX

topics, which is structure oriented. Note that we ob-

tain 0.502 for the most structured topic (for MAep

and f

strict

) over INEX 2005 topics, which conﬁrms

the effectiveness of our approach in highly structured

queries context on one hand, and the impact of struc-

ture on XML retrieval on the other.

Additional experiments have been undertaken to

show the effectiveness of our query reformulation

approach. Since INEX does not provide a training

dataset, we built it manually by dividing the INEX

corpus into a training dataset containing 450 docu-

ments and the 16369 remaining documents are used

as a test corpus. To evaluate the impact of the query

reformulation, we use the same XML retrieval pro-

cess as described below.

In Table 1 we present a comparison between the

values obtained before reformulation (BR), after re-

formulation (AR) and the mean average of the ofﬁcial

results of all INEX participants (AVR). The parame-

ters δ and γ are respectively 0.70 and 8.50.

We can see through our experiments that our

query reformulation approach signiﬁcantly improves

the results on the f

generalized

quantization function

(until 0.38 %) which considers one element to be rel-

evant provided that it is both exhaustive and speciﬁc.

This function is an excellent illustration of structured

information retrieval. We note that during these ex-

periments we reformulate only the queries structures

without changing their original content, and therefore

we believe that this reformulation has brought an evo-

lution that could be accentuated by the reformulation

of the content.

STRUCTURE-BASED INTERROGATION AND AUTOMATIC QUERY REFORMULATION

127

Table 1: Comparative results before and after automatic

query reformulation.

Quantization Run MAep

BR 0.099

strict

AR 0.10076

AVG 0.0286

BR 0.0794

gen

AR 0.0832

AVG 0.0526

BR 0.0275

genLifted

AR 0.0279

AVG 0.0197

6 CONCLUSIONS

We have presented in this paper an XML retrieval ap-

proach based on tree matching. The approach con-

sists of comparing document and query representa-

tions, computing a structure and a content score to

each document node and then combine them into a

ﬁnal score.

Each score is computed independently of the

other, and the ﬁnal score depends on both of them.

Undertaking content and structure scores computa-

tion independently leads to the independencebetween

content and structure scores distributions. This as-

sumption is needed to estimate the score of each doc-

ument node by its probability of relevance.

We also proposed a representation of the original

query and relevant fragments under a form of a ma-

trix. After some processing and calculations on the

obtained matrix and after some analysis we have been

able to identify the most relevant nodes and their re-

lationships that connect them. The obtained results

show that the automatic reformulation of the query

structure contributes to the improvement of XML re-

trieval. The strategy of the reformulation is based on

a matrix representation of the XML trees deemed rel-

evant to the fragments and the original query.

We experimented our approach into a dataset pro-

vided by INEX. We have placed the emphasis on the

CAS tasks, which represent an excellent illustration

of ﬂexible XML retrieval. This task is the most ap-

propriate for our retrieval model. The system was de-

signed especially for such tasks.

Additional experiments have been undertaken to

show the effectiveness of using an automatic query

reformulation model. Through our experiments, we

show that the structure hints are very important not

only for XML retrieval but also for XML query refor-

mulation.

REFERENCES

Balog, K., Bron, M., and de Rijke, M. (2010). Category-

based query modeling for entity search. 32nd Eu-

ropean Conference on Information Retrieval, ECIR,

pages 319–331.

Ben Aouicha, M., Tmar, M., Boughanem, M., and Abid, M.

(2006). Vers une stratgie de recherche d’information

structure base sur la comparaison d’arbres. CORIA,

pages 65–72.

Ben Aouicha, M., Tmar, M., Boughanem, M., and Abid, M.

(2009). Experiments on element and document statics

for xml retrieval based on tree matching. International

Journal of Computer and Information Science and En-

gineering, IJCISE, 3(1):7–16.

Bordogna, G. and Pasi, G. (2000). Flexible querying of

structured documents. Proc. of the fourth Interna-

tional Conference on Flexible Query Answering Sys-

tems(FQAS).

Fuhr, N. and Grossjohann, K. (2001). Xirql: A query

language for information retrieval in xml documents.

Proc. of the 24th annual ACM SIGIR conference on

research and development in Information Retrieval,

New Orleans, USA, pages 172–180.

Piwowarski, B. and Dupret, G. (2006). Evaluation in (xml)

information retrieval: Expected precision-recall with

user modelling (eprum). Proc. of the 29th annual

ACM SIGIR conference on research and development

in Information Retrieval, pages 260–267.

Rocchio, J. (1971). Relevance feedback in information re-

trieval. Prentice Hall Inc., englewood cliffs, nj edition.

Schlieder, T. and Meuss, H. (2002). Querying and ranking

xml documents. Journal of the American Society for

Information Science and Technology, 6(53):489–503.

Selkow, S. M. (1977). The tree-to-tree edition problem. In-

formation processing letters, pages 184–186.

KMIS 2011 - International Conference on Knowledge Management and Information Sharing

128