
SEMANTIC MINING OF DOCUMENTS
IN A RELATIONAL DATABASE
Kunal Mukerjee, Todd Porter and Sorin Gherman
SQL Server RDBMS, Microsoft, Redmond, WA, U.S.A.
Keywords: Semantic mining, Documents, Full text search, SQL Server.
Abstract: Automatically mining entities, relationships, and semantics from unstructured documents and storing these
in relational tables, greatly simplifies and unifies the work flows and user experiences of database products
at the Enterprise. This paper describes three linear scale, incremental, and fully automatic semantic mining
algorithms that are at the foundation of the new Semantic Platform being released in the next version of
SQL Server. The target workload is large (10 – 100 million) enterprise document corpuses. At these scales,
anything short of linear scale and incremental is costly to deploy. These three algorithms give rise to three
weighted physical indexes: Tag Index (top keywords in each document); Document Similarity Index (top
closely related documents given any document); and Phrase Similarity Index (top semantically related
phrases, given any phrase), which are then query-able through the SQL interface. The need for specifically
creating these three indexes was motivated by observing typical stages of document research, and gap
analysis, given current tools and technology at the Enterprise. We describe the mining algorithms and
architecture, and outline some compelling user experiences that are enabled by these indexes.
1 INTRODUCTION
Managing unstructured and structured data in
separate systems leads to many problems, such as
consistency control, synchronizing backups, and
supporting multiple systems. Increasingly, this pain
drives users to move unstructured data into relational
databases. Such unstructured data includes files
(e.g., office documents, PDFs) and large text
fragments (e.g., emails, wiki pages, forum
comments), etc.
As users store more documents in databases, it is
critical that databases help manage them. Doing so
effectively requires more than storing and retrieving
bits; it requires providing access to the information
in documents. To illustrate, suppose a consumer
products company keeps corporate documents in a
database. These documents describe which
employees work on which products, how products
are related, how they compare to the competition,
etc. However, if the database treats these documents
merely as opaque bits, users cannot query this
information. To address this, we introduce the
Semantic Platform for SQL Server, which mines and
then exposes structured concepts within unstructured
data to database queries, by building three physical
indexes: 1) Tag Index (TI), which can return the top
keywords, given a document; 2) Document
Similarity Index (DSI), which can return the most
closely related documents, given any document; and
3) Semantic Phrase Similarity Index (SPSI), which
returns the top semantically related phrases, given
any phrase.
The view from one level up is that in SQL
Server, we are building a tightly streamlined and
integrated Document Understanding Platform,
comprising Integrated Full Text Search (IFTS) and
Semantic Platform for documents, under a unified
functional surface of SQL language extensions. We
avoid creating an entirely separate syntax for
Semantic Platform, by merely extending the IFTS
syntax that is already familiar to many customers.
The processing flow and algorithms are highly
optimized so that documents are crawled, parsed and
mined in a unified, 1-pass algorithm. The algorithm
is incremental, and efficiently updates the index as
the corpus evolves over time (increments may be
triggered both manually and automatically). The
Full-Text Index (FTI) is one output, in order to
satisfy the needs of document search.
Simultaneously, document level semantics are
mined into the three new indexes: TI, DSI, and
146
Mukerjee K., Porter T. and Gherman S..
SEMANTIC MINING OF DOCUMENTS IN A RELATIONAL DATABASE.
DOI: 10.5220/0003631401380150
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 138-150
ISBN: 978-989-8425-79-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

SPSI, without needing to re-crawl and re-parse the
original documents.
Additionally, the user does not have to go
through any special configuration steps in order to
tell the system about their data, e.g. set up special
classifiers, etc. Everything involved in mining these
indexes, figuring out what are the semantic concepts
contained in the document corpus, how they cluster,
etc., is fully automatic and inherent to the system.
This means that we have created a very low barrier
to entry for users of the document understanding
system.
We conducted experiments to verify two main
properties: linear scalability and quality. Results
show that building the FTI, TI, and DSI is linear and
highly scalable. Also, experimental results show that
both TI and DSI produce competitive precision
numbers when compared to other methods.
The rest of the paper is organized as follows:
Section 2 describes related products and algorithms
and then describes how we used customer and
scenario focused design to help guide our design. In
Section 3, we describe the overall architecture and
algorithmic components. Experimental results are
described in detail in section 4. We describe some
potential applications in Section 5, and conclude and
point to future work in Section 6.
2 ALGORITHMIC LINEAGE
AND DESIGN OBJECTIVES
Starting in February 1990, the NSF has been
publishing a set of goals for database research and
commercialization every 5 years. The NSF
prospectus (Silberschatz, 1996) clearly identifies the
need to cover IR over unstructured and semi-
structured data and document processing, as a large
emerging need for future database product lines.
Fifteen years later we have Full-Text Search
trending towards mainstream in multiple database
product lines including Microsoft SQL Server;
Oracle acquiring OpenText in 2008, etc.
We are currently at the cusp of widespread
adoption of document IR in the database, as
predicted by leading NSF researchers. In the
Enterprise space, Oracle, PostgreSQL, Microsoft
and others are competing in order to become
entrenched players in the space of Document
Understanding. Oracle's Open Text (McNabb, 2007)
has created integration with Share Point and
Microsoft Duet (Office + SAP). Oracle Open Text
offers a broad based document strategy, providing
good support for web docs, via their Red Dot
component, and over semi-structured data, by way
of LiveLink. Semi-structured search is also
supported with LiveLink ECM (McNabb, 2007).
Microsoft’s primary products in the space of
document understanding include SharePoint and
FAST, and also in-database IFTS, which has been
offered for a few releases now.
At the algorithmic level, two semantic mining
classics are Latent Semantic Indexing (LSI)
(Deerwester, 1988), Probabilistic LSI, or PLSI,
(Hofmann, 1999), and Latent Dirichlet Allocation
(LDA) (Blei, 2003). These have been extensively
used and built upon, in both Enterprise and Web
based search. There are a number of approaches for
extracting relevant keywords from a document, e.g.
(Cohen, 1995).
The main advantages of our semantic mining
algorithms over the existing algorithms are that our
algorithms scale linearly with the size of data, and as
we show in the results section (Section 5), linear
scale-out is achievable with additional
computational resources. They are also incremental
in nature. All of these are essential ingredients for
mining large (e.g. 10 to 100 million) Enterprise
document corpuses and keeping the indexes “fresh”
as the corpus evolves over time.
There are some similarities of our Semantic
Phrase Similarity Indexing (SPSI) approach with
PLSI: both these are statistically based and
incremental; however, our approach takes a
simplifying assumption over co-occurrences: that of
i.i.d (independent and identical distributions), and
generates the co-occurrence weights explicitly via
Jaccard similarity, and propagates weights explicitly,
via transitive closure. These explicit assumptions
and operations are very useful for rigorous
testability, in the application context of deploying in
a relational database.
In (Damashek, 1995) the authors propose a
language-independent means of gauging topical
similarity in unrestricted text, using character level
n-grams and a simple vector-space technique to infer
categorization and similarity. By contrast, we
bootstrap our system with fairly large and complete
statistical language models (LM), and work with
ngrams over LM words that are output by the word
breakers in our system (Full Text Search Overview),
to cheaply inject high level structural and contextual
constraints into our feature space very early on
(almost at the outset). This saves compute time for
our system.
In a related work also based on character level n-
grams (Cohen, 1995), the authors are motivated to
SEMANTIC MINING OF DOCUMENTS IN A RELATIONAL DATABASE
147

construct a highlight/abstract extraction system that
does not rely on any language-specific resources
such as stemmers and stop lists, whereas the
scenario is exactly opposite for IFTS and Semantic
Platform in SQL Server, where the language is
explicitly identified, and space constraints are not as
tight. So we do employ stop lists, stemmers and
sophisticated LMs as relatively cheap components
from our perspective, to reduce CPU load, which
aligns better with the more imperative aspects of our
typical customer workload.
In (Gabrilovich, 2007) the authors do inject
language specific resources; they go one step further
and use a knowledge model based on training a
space of concepts on Wikipedia. Their Explicit
Semantic Analysis (ESA) system reports good
correlation with subjective evaluation, and also has
the advantage of working over a vector space that
makes intuitive sense compared to the above
character-based vector space methods.
However, at the Enterprise (the primary domain
for SQL Server), a lot of the information tends to be
very domain-specific, technical, and full of jargon
and acronyms. For this reason we construct a system
that does use a vector space of language ngrams, but
stops short of constructing a vector space over a
generic knowledge model, because we have found
that these tend to be too generic.
For document similarity, our approach is close to
the classic vector space model (Salton, 1975). We
use cosine-similarity over the documents represented
in the vector space of weighted keywords, and use
LM entropy to boost semantic salience to correlate
well with subjective evaluation.
Our approach to phrase similarity is close to
(Hammouda, 2004). Whereas their objective is to
ultimately use the phrase graph to infer document
similarity, ours is to infer a semantic thesaurus that
incorporates transitive relationships between
phrases.
We also focus on scalability aspects and linear
approximation whilst generating a transitively closed
phrase graph, because linear scale is pretty much a
hard pre-requisite for SQL Server’s customer base.
Most important from our perspective is the fact that
our mining algorithms are tightly integrated as a
cohesive system such that the documents are parsed
or incrementally scanned in a single pass, and all the
data flows linearly through the entire system to
create the three new indexes, plus the already
Figure 1: System design directly mirrors typical customer activities in researching large document corpuses: 1) FT1 enables
full text search, returning references to the most relevant documents; 2) The next step is to query top documents for most
relevant keywords and phrases – this is facilitated by T1; 3)The subset of interesting documents is used to query all related
documents, using the DSI; and 4) Search terms are refined by way of SPSI (not shown here) – this takes us back to step 1.
Key Title Document
D1 Annual Budget …
D2 Corporate
Earnings
…
D3 Marketing Reports …
…… …
---------------
---------------
---------------
---------------
----------
---------------
---------------
---------------
---------------
----------
---------------
---------------
---------------
---------------
----------
ID Keyword Colid … compDocid CompOc CompPid
K1 revenue 1 … 10,23,123 (1,4),(5,8),(1,34) 2,5,6,8,4,3
K2 growth 1 … 10,23,123 (1,5),(5,9),(1,34) 2,5,6,8,5,4
… ……… … …
DocID MatchedDocID
D1 (Annual Budget)D2 (Corporate
Earnings)
D1 (Annual Budget)D7 (Finance Report)
D3 (Marketing Reports)D11 (Azure Strategy)
……
ID DocID
T1 (revenue growth)D1 (Annual Budget)
T1 (revenue growth)D2 (Corporate Earnings)
T2 (Windows Azure)D3 (Marketing Reports)
……
T1 (revenue growth)D7 (Finance Report)
……
T2 (Windows Azure)D11 (Azure Strategy)
……
ID Keyword
T1 revenue
T1 growth
T2 Windows
T2 Azure
……
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
148
existing FTI. Additionally, the one pre-existing and
three new indexes are created and maintained to
directly support four very fundamental customer
needs and interactions, which are described next.
This makes the end-to-end system highly optimized,
and ensures that all functionality and end outputs are
directly motivated by customer requirements.
2.1 Customer and Scenario Focused
Design
Customer focus groups reveal that the following is a
common work flow of events and actions when
perusing and researching a document corpus, as
depicted in Figure 1: 1) First, the user, by now very
accustomed to using search engines, starts by
searching the corpus for an idea, a word or a phrase;
2) Next, when the search returns a number of “hits”
comprising enterprise documents, the user needs to
quickly skim the top results for their content without
reading the entire document – this is an important
differentiator for the Enterprise user as opposed to
the user of web search, because Enterprise
documents may be hundreds of pages long, whereas
web pages are short enough to be scanned rapidly; 3)
When a small number of candidate documents have
been identified, the user wishes to round off their
search by querying for all documents that are related
to those exemplars – without this the research would
not be complete; and 4) Finally, the user may wish
to re-submit a search by refining the search terms,
typically by seeking out semantically related words
or phrases. For instance, “Google” may translate into
{search engine, relevance} by way of ordinary
thesaurus lookup; however, a semantically related
term for “Google”, when mined over a corpus of
Microsoft documents, might result in “competition”.
With the results of step 4, the user returns once
more to step 1, and the process refines and repeats
until the research is completed. The fundamentals of
system design of Semantic Platform follow almost
directly from the above work flow. Internally, we
provide four physical indexes to support the above
queries. 1) FTI, already available in past releases of
SQL Server, enables searching of words and
phrases; 2) TI summarizes each document into its
top phrases; 3) DSI finds the top related documents
to a given document; and 4) SPSI provides
semantically related phrases to a given phrase.
The family of mining algorithms that processes a
large enterprise document corpus linearly and
incrementally to produce the above four indexes,
constitutes a significant advance in the state of art,
because they may be applied to unify the search and
semantic inference processing suites of a
significantly large number of Enterprise products.
With modifications to handle spam and account for
web-specific relevance characteristics such as
hyperlink count (page rank), they may become
interesting for search engines. Our algorithms can
provide substantial savings of capital expenditure as
well as reduce document crawl- to-index
availability, i.e. end-to-end throughput and latency
of these products may be improved.
In this paper, we present the Semantic Platform
being released in the next version of SQL Server.
This paper specifically describes the underlying
mining algorithms of Semantic Platform, and
provides a brief outline of the SQL extensions and
new user experiences that are easy to build by
querying these indexes.
3 SEMANTIC MINING
ALGORITHMS AND
ARCHITECTURE
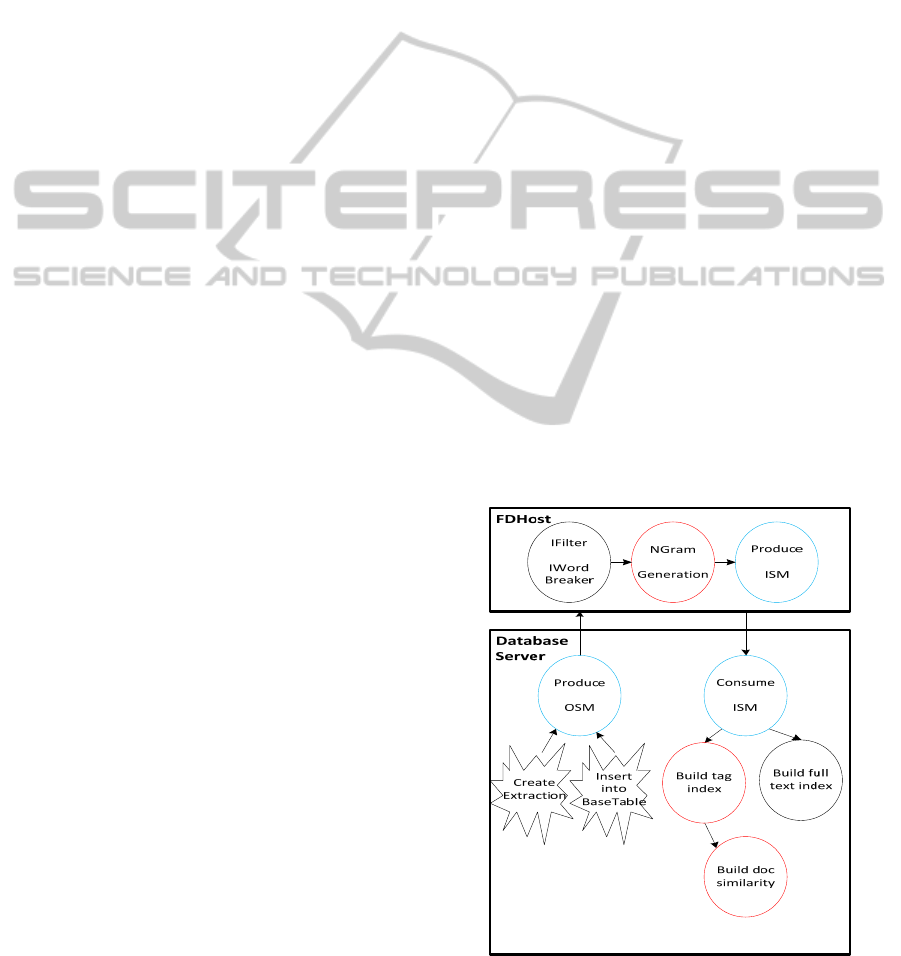
In this section, we first show the system level block
diagram, which shows how all the algorithmic
pieces of IFTS and Semantic Platform fit, and how
data flows through the tightly combined IFTS and
Semantic Platform system end-to-end. Next, we will
provide details on the three new Semantic mining
algorithms.
Figure 2: High level system architecture.
SEMANTIC MINING OF DOCUMENTS IN A RELATIONAL DATABASE
149

3.1 Top Level System Diagram
Figure 2 shows how all the pieces fit at the system
level. We start with a table in SQL database, where
one column contains references (e.g. URIs) to actual
documents. If the source of the data resides in a
relational database, the primary key in the relational
table or view goes in the main document index key
field. Once the extraction process is created and
launched by the user, the documents are crawled and
parsed in a separate process called FDHost, which
runs as a service, hosting third party DLLs such as
IFilters and word breakers, which crack open the
document formats, e.g. *.doc, *.pdf, and extract
words and word sequences (ngrams). Shared
memory is used for inter-process communications
between the database server processes.
Once the ngrams have been received back in the
database server process, the TI and FTI are built
and/or incremented concurrently. After the TI has
been built, it is in turn used as the source to
construct the DSI. After DSI is built or incremented,
the whole process is complete. Thus, this provides a
streamlined, single-pass and highly optimized
combined architecture for IFTS and Semantic
Platform in SQL Server.
Due to the close integration of the Semantic
mining platform with the pre-existing Full Text
Search pipeline, the cost/effort to develop and
maintain this architecture is moderate. We took 8
months with a team of 6 Developers, 5 Testers and 1
Program Manager to productize the system from
start to finish.
3.2 Mining the Tag Index
The primary objective of mining the tag index (TI) is
the need to summarize long enterprise documents
(sometimes 200 – 500 pages long) into their top few
key words and phrases. This is very important in
order to support the search experience at the
Enterprise, because the user might otherwise find
search results, which are links to long documents,
very time consuming to go through. Good tag
indexing therefore directly results in productivity
gains for the user of an Enterprise search based
system such as IFTS.
The TI mining algorithm is based on a LM and
weight and threshold functions. TI is the output of
the algorithm: given a document id, the TI returns a
list of its top N key phrases, each with a weight
signifying relative importance in the document.
The data flowing into the TI mining algorithm is
shown in the system block diagram above (Figure
2). The TI mining algorithm is kept simple for
scalability purposes, and is based on cross-entropy:
we compare the word distributions from the LM
(which contains expected distributions) to the word
distribution from the current document. We score
the ngrams based on how much more frequently
they appear in a document, compared to their
expected frequency as computed based on LM. This
can be viewed as an approximation to Term
Frequency Inverse Document Frequency (TFIDF)
weighting, but we are replacing the inverse
document frequency with the LM frequency. This
enables our algorithm to be corpus independent,
which is essential for Enterprise document corpuses
that are getting new documents daily – we do not
want to re-compute the TI every time this occurs.
Also, our algorithm is not machine learning based,
so there is no training phase, it can be used without
the need of a good corpus representative sample data
set for initial training.
A caveat is that for short documents the word
distributions are not very reliable. Therefore, we
take into account document length as well. For all
ngrams in any document that are considered as a
possible tag, the algorithm requires: 1) Ngram
frequency in the document; and 2) Ngram frequency
in the language. This is either directly available in
the LM, or is inferred from the LM, by treating
words as i.i.d and adding their log probabilities.
The pseudo-code for extracting keywords is
provided below.
ExtractTopNKeyPhrases(doc)
{
languageModel Å
SelectLanguageModel(doc);
candidates Å
Empty topN priority queue;
for each ((ngram, locations) in doc)
do
score = CrossEntropy(doc.GetSize(),
locations.Length,
// ngram frequency in doc
languageModel.Frequency(ngram)
);
Candidates.Add(ngram, score);
end for
return topN candidates by descending
score
}
ComputeCrossEntropy(docSize,
docFrequency,
LMFrequency)=(docFrequency/docSize)
x(BASE
Log10(LMFrequency)
)
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
150

3.3 Mining the Document Similarity
Index
The DSI mining algorithm works with a populated
and stable TI as its input/data source. The end output
of the algorithm is an index which can be queried by
any given document id, and returns the top N other
documents which share common highly ranked key
phrases with the given document, with connection
weights for each related document. Whereas
incrementing the TI is straightforward: on getting
new documents we simply add new rows to the TI,
incrementing the DSI is somewhat complex, because
it may include changing existing rows in the table.
Therefore, we present both the basic DSI mining
algorithm, and the incremental algorithm in this
section.
We only consider up to top K′ candidate
documents that we consider for similarities (to avoid
the O(N
2
) CPU issue), and only top K (where K ≤
K′) of those similarities will be stored. This allows
us to avoid the O(N
2
) space issue. This greedy
heuristic can be summarized as: given the target doc
T, we have the list of keywords in descending order
by their relative weight within T given by the TI; we
start exploring the keywords list top-down and we
find the documents where these keywords are also
highly weighted; we stop when we have found K′
such documents, or we finished exploring the
keywords list for doc T; those K′ documents are our
candidates.
Given two documents, doc1 and doc2, the TI
gives us the list of tags and corresponding weights
for each:
Doc
1
: {(tag
11
, weight
11
), (tag
12
, weight
12
),…,
(tag
1k
, weight
1k
)}
Doc
2
: {(tag
21
, weight
21
), (tag
22
, weight
22
),…,
(tag
2k
, weight
2k
)}
We use cosine-similarity to compute the
similarity between two documents, as shown below:
(
,
)
=
(
,
)
(
)×(
)
where:
(
,
)=
∑
{ℎ(,
)×ℎ(,
)}
for each tag that is common to doc
1
and doc
2
,
and
2
),()(
∑
=
ii
doctagWeightdocNorm
for each tag
in doc
i
.
The pseudo-code for the DSI mining algorithm is
provided below.
ExtractTopKDocumentSimilarities(TagInde
x TI)
{
for each (unprocessed docId) do
// Step 1: Find top K’ candidates
topK’Candidates
=SelectSimCandidates(TI, docId);
// Step 2: Find similarities,
// relative to candidates
resultsHeap <-EmptyHeap(size=K);
for each (candidateId in topK’) do
similarity=CosineSimilarity(T,
docId,candidateId);
resultsHeap.Add(candidateId,
similarity);
end for
// Step 3: Select top K results
for each
(candidateId,similarity) in
resultsHeap do
DSI.WriteRow(docId,candidateId,
similarity);
end for
end for
}
The details of the SelectSimCandidates function
are provided in pseudo-code.
SelectSimCandidates(TI, docId)
{
resultSet = Empty(Map<int, double>);
for each (tag, weight1) in
TI(docId) do
for each ((candidateId, weight)
in (select topK’ docs from
TI[tag]) do
if (candidateId ∉ resultSet)
resultSet.Add(candidateId,0.0);
end if
resultSet[candidateId]
+= weight1*weight2;
end for
end for
return top K items in resultSet;
}
3.3.1 Incremental DSI Algorithm
When the corpus evolves as new documents are
added, and older documents are updated and deleted,
it is not immediately obvious how to update the DSI
such that it remains “fresh”, as well as consistent
with the TI and FTI, without having to re-build it
from scratch each time, as that would be very costly.
We have designed a scalable approach to this
problem, which builds upon the candidate selection
SEMANTIC MINING OF DOCUMENTS IN A RELATIONAL DATABASE
151
heuristic that is at the core of our DSI mining
algorithm (see pseudo-code segments above).
For the documents in the update batch, (doc
1
,…,
doc
N
), we first extract and store the tags in the Tag
Index (TI). Then we compute document similarities
for each of doc
1
,…,doc
N
.
Let us detail the process for any one document in
this batch, doc
j
. We apply the standard DSI
algorithm for doc
j
and find the top K′ candidates for
it: cand
1
,…,cand
K′
, where each of the K′ candidates
can either be one of the documents already indexed
in previous batches, or it can be a document from the
same batch as doc
j
.
For the incremental step, we do the following for
each cand
j
in top K′: 1) If cand
j
is a document in the
current batch, do nothing special (since its
similarities will be up to date); 2) If cand
j
is a
document from a previous batch, compare
Similarity(doc
j
, cand
j
) with the weakest similarity
among the top-K similarities stored for cand
j
; if
there is a document X such as Similarity(cand
j
, X) <
Similarity(doc
j
, cand
j
), then we update the stored top
K similarities for cand
j
, by replacing
Similarity(cand
j
, X) with Similarity(doc
j
, cand
j
).
We will discuss the cost and accuracy
implications of the incremental algorithm in the
section on Experimental Results.
3.4 Mining the Semantic Phrase
Similarity Index (Graph)
N.B: This index is not being shipped in the next
version of SQL Server, but in a subsequent release
to be determined by Microsoft.
In this section we first describe the top level
objectives of the information we are trying to mine,
to clarify for the reader, fundamental differences
with related approaches like (Hammouda, 2004).
Whereas the end objective in (Hammouda, 2004) is
to infer document similarity, our objective is to infer
a phrase similarity graph that is approximately
closed under transitive closure, and has near-linear
time computational requirement.
3.4.1 Top Level Objective: Semantic
Thesaurus
The overall objective of mining the semantic phrase
similarity index (SPSI) is to derive a semantic
thesaurus which embodies the inferred semantic
space over phrases used at the Enterprise.
For example, given a Microsoft corpus of
documents, we would like “Google” to translate into
things like “search engine”, “ad revenue”, etc., that
we would normally get from a Thesaurus lookup,
but additionally, also get “competition”. In case the
corpus is mainly discussing the competition between
these companies, we want “competition” to be
heavily weighted. We also wish to discover so-
called latent relationships (Deerwester, 1988),
between words and phrases, such that if A Æ B with
a high weight and B Æ C with a high weight, then I
wish to infer the A Æ C relationship. Most
importantly, we wish to construct the mining
algorithm to scale linearly, be incremental, and
possible to integrate tightly into the overall FTI and
Semantic Platform architecture outlined in Section
3.1.
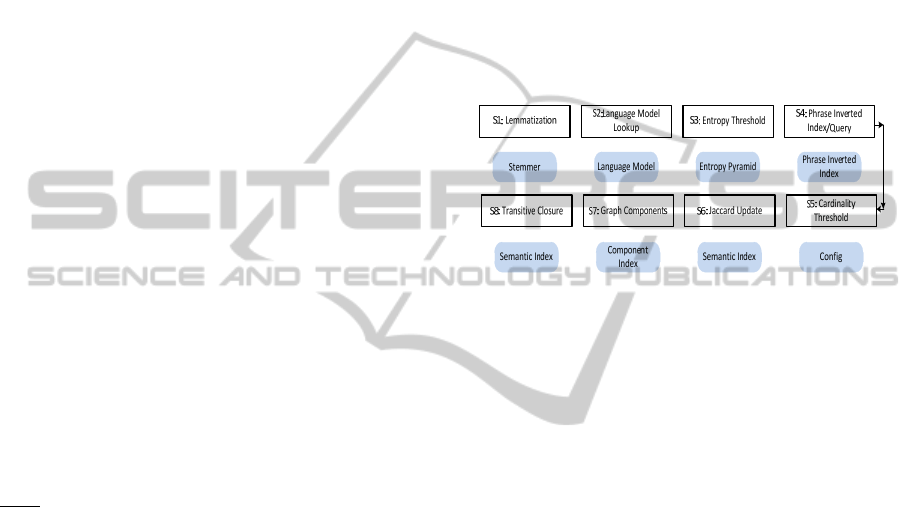
Figure 3: SPSI mining algorithm.
3.4.2 Eight Stage Algorithm
The SPSI algorithm consists of eight stages,
numbered S1 – S8 in Figure 3. Corresponding to
each stage is a data structure abstraction, as shown
in the figure.
To facilitate understanding this algorithm, we
will re-use a worked example from (Zamir, 1998).
Consider that the document corpus we are working
with contains the following three documents, with
ids: D
1
, D
2
and D
3
.
D
1
: “Cat ate cheese”
D
2
: “Mouse ate cheese too”
D
3
: “Cat ate mouse too”
In S1, which does tokenization and
lemmatization into base forms, we transform the
corpus thus:
D
1
: “cat eat cheese”
D
2
: “mouse eat cheese too”
D
3
: “cat eat mouse too”
In S2 we simply substitute LM ids for each word
(or ngram), so that the rest of the algorithm works
with integers. This makes the processing more
efficient than working with strings. However, for
ease of explanation, we will revert back to using
strings for the remainder of this worked example.
D
1
: 2022, 788, 4077
D
2
: 16788, 788, 4077, 345
D
3
: 2022, 788, 16788, 345
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
152

In S3, where we use an LM to filter out the low
entropy words in the language, we end up with the
following:
D
1
: “cat eat cheese”
D
2
: “mouse eat cheese too”
D
3
: “cat eat mouse too”
We pre-process the text using LMs to derive
entropy sliced pyramids (ESP). The top levels of
these pyramids contain the most salient semantic
entities. Lower levels of the ESP contain
progressively more terms, and the lowest level
contains everything and can be used for full text
search. ESP essentially gives us a multi-resolution
decomposition of the data, and imposes the
priority/scale constraints that the top levels of the
pyramid contain both the most semantically valuable
as well as least quantity of data, which means we
can “skim off the top” and compute only the most
salient information, entities and relationships faster
than the rest. This mechanism enables us to deal
very effectively with information at scale. Figure 4
shows an example of using an ESP on the incoming
text (presumably from a resume): “Skill set: I have
used C++ and MATLAB”.
Figure 4: Entropy Sliced Pyramid. Each level contains
terms at or above the entropy threshold for that level.
In S4, we create the inverted ngram index, as
shown below:
“cat”: {D
1
, D
3
}
“cheese”: {D
1
, D
2
}
“mouse”: {D
2
, D
3
}
“cat cheese”: {D
1
}
“mouse cheese”: {D
2
}
“cat mouse”: {D
3
}
Here it’s worth mentioning that we only used 1,
2, and 3-grams. There is a big space/disk cost to
using high order ngrams, and we repeatedly found
evidence of diminishing returns for ngrams longer
than 3 in a number of large (Enterprise) corpuses.
This is shown in Figure 5.
In S5 we filter out sets with cardinality less than
some threshold. For example, in our running
example, we may filter out the sets: “cat cheese”,
“mouse cheese” and “cat mouse” because they are
all singletons. Sometimes singleton sets are indicative
Figure 5: Ngram node length histogram mined from a
3000 doc corpus.
of noise, and they are rarely useful in linking
semantically similar content.
In S6, we create weighted adjacency lists, using
the Jaccard metric:
∪
∩
||
||
),(
21
21
21
DD
DD
DDJ =
. This
provides a notion of semantic nearness between any
two ngrams, as the count of documents they are both
present, over those only one is present. In our
running example, the pairwise Jaccard metric
applied to the surviving ngrams produces the
following output, which is an Adjacency Matrix:
cat: {(cheese, 0.33), (mouse, 0.33), (cat cheese,
0.5), (cat mouse, 0.5)}
cheese: {(cat, 0.33), (mouse, 0.33), (cat cheese,
0.5), (mouse cheese, 0.5)}
mouse: {(cat, 0.33), (cheese, 0.33), (mouse
cheese, 0.5), (cat mouse, 0.5)}
cat cheese: {(cat, 0.5), (cheese, 0.5)}
mouse cheese: {(cheese, 0.5), (mouse, 0.5)}
cat mouse: {(cat, 0.5), {mouse, 0.5)}
For S6, we compute the Jaccard graph that
relates all pairs of ngram nodes incrementally, with
each incoming document, as described below.
Induction Hypothesis: Graph is Jaccard complete
(i.e. all pairs have distance given by the Jaccard
metric) after we have seen the (i-1)
th
document.
Induction Step: We only partially update the
graph to change numerators and denominators of
only the “active ngrams” – these are the ngrams that
occur in the i
th
document. After the update step the
graph is once more Jaccard complete.
In the following we outline the steps of the fast
Jaccard update algorithm on receiving the ith
document.
1. Represent the incoming document as a set of
ngrams: Doc(i) = {ng
j1
, ng
j2
, …, ng
jn
};
2. Mark previously unseen and previously seen
ngrams, creating the set partitions:
∪
)()()( iUnseeniSeeniDoc =
;
SEMANTIC MINING OF DOCUMENTS IN A RELATIONAL DATABASE
153

3. Insert the unseen set into the Adjacency
Matrix, the unseen rows become: Doc(i), all
numerators and denominators = 1;
4. For each ngram in the Seen set, append the
Unseen set, and initialize all numerator =
denominator = 1;
5. For each ngram in Seen set, update the old row
with denominator++; and if the old word is in
Doc(i) then numerator++.
6. In order to guarantee strictly linear behaviour
wrt Jaccard updates, we reuse the incremental
update regime detailed in the context of DSI
updates in section 3.3.1. Namely, we maintain
a maximum of K’ candidates in each word’s
adjacency list; these are used to “bubble up”
the final K top relationships for each word. K’
> K.
Step S7 is actually an optimization/pre-
processing step to speed up S8, and so we first
describe S8, which is the transitive closure over the
graph obtained from S6.
At the output of S6, we have a pairwise
connected weighted graph represented by the
adjacency matrix. From this it is possible to compute
connected components and semantic clusters and
neighbourhoods. Indeed, that is what we do in S7.
However, in order to capture the latent semantic
relationships, it is necessary to consider transitive
relationships between ngram nodes. If we fail to do
that, the semantic inference available from the entire
process tends to be locked into “vocabulary silos”.
We compute the transitive closure over this
graph using the classic Floyd-Warshall algorithm, by
defining the relaxation step to be the maximum over
edge weight between vertices i, j, and intermediate
vertex k: e(i, k) x e(k, j). This exposes the latent
semantic relationships, and gives us functional
equivalence with LSI. The end result is an entity
relatedness graph with edge weights representing
relationship strengths between any pair of vertices.
Note that our edge weights are symmetrical, and so
we only need to deal with the upper triangular half
of the adjacency matrix, discounting diagonal entries
(each node is trivially related to itself).
Theorem: Given a Graph G, defining the
relaxation step on an edge connecting vertices V
i
and
V
j
as: e(i, j) = Max{e(i, j), e(i, k) x e(k, j)} where the
base edge weights represent Jaccard similarity, is
necessary and sufficient to induce transitive closure
over G, exposing latent semantic relationships.
Proof: If Jaccard similarity is considered as an
approximation of probability that nodes V
i
and V
j
are
related, and if the relationship between any two
(non-identical) pairs of vertices (e.g. {V
i
, V
j
} and
{V
i
, V
k
}) is independent, then their joint probability
is the result of multiplying independent probabilities.
But this is the same as multiplying edge weights
stemming from Jaccard similarity.
To complete the running example, here are the
outputs of the Transitive Closure step. Latent
relationships that emerge after transitive closure are
highlighted.
cat: {(cheese, 0.33), (mouse, 0.33), (cat cheese,
0.5), (cat mouse, 0.5), (mouse cheese, 0.165)}
cheese: {(cat, 0.33), (mouse, 0.33), (cat cheese,
0.5), (mouse cheese, 0.5), (cat mouse, 0.165)}
mouse: {(cat, 0.33), (cheese, 0.33), (mouse
cheese, 0.5), (cat mouse, 0.5), (cat cheese,
0.165)}
cat cheese: {(cat, 0.5), (cheese, 0.5), (mouse,
0.165), (mouse cheese, 0.25), (cat mouse,
0.25)}
mouse cheese: {(cheese, 0.5), (mouse, 0.5),
(cat, 0.165), (cat cheese, 0.25), (cat mouse,
0.25)}
cat mouse: {(cat, 0.5), {mouse, 0.5), (cheese,
0.165), (cat cheese, 0.25), (mouse cheese, 0.25)}
3.4.3 Transitive Closure Optimizations
Transitive Closure on a graph is an expensive O(N
3
)
operation. We outline a series of optimizations that
reduce the end-to-end complexity.
First, we enforce sparseness on the graph from
S6 by clamping weights, e(i,j), that are less than a
sparseness threshold, T, to zero: If (e(i, j) < T e(i, j))
= 0, then e(i,j) = 0.
We next run connected components algorithm on
the sparse graph. Connected components is O(N).
Once the M components are identified, the transitive
closure on the entire graph reduces to running
transitive closure on the M components. Thus, we
transform the overall complexity from O(N
3
) to
)(
0
3
∑
=
M
i
i
nO
.
A spin-off data structure of connected
components is the Component Index, which is
actually a hierarchy of embedded sub-components,
corresponding to different values of sparseness
threshold. This enables us to work with components
and clusters later on.
We now state without formal proof, a conjecture
based on substantive empirical evidence, that
actually results in completely eliminating the
expensive transitive closure operation for large
corpuses. Either transitive closure is necessary and
the document set is small, in which case it is cheap
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
154

to compute; or transitive closure is asymptotically
unnecessary (and can therefore be entirely
eliminated), beyond filling in the pair-wise Jaccard
similarities, when the document set is large.
Intuitive Explanation: Consider documents
relating Obama and the US presidency. These are
likely to be many. Consider documents relating
Obama and basketball. These are likely to be few. In
a small collection there may not be any single
document commenting on relationships between the
office of the President of USA and basketball.
However, if a sufficiently large document set is
constructed, then there is a high chance that some
document does talk about how presidents relate to
the game of basketball.
This intuitively explains why the net contribution
of transitive closure, or latent relationships, in
general, may be expected to diminish as we
approach very large document sets.
Experimental Evidence: We now present the
experimental evidence (Figure 6) which shows that
the contribution of the weight deltas due to the
transitive closure step seems to follow roughly an
exponential decay curve as the corpus size increases.
We have found that this generalizes over a variety of
different Enterprise (e.g. SharePoint design
document repository) and academic corpuses (e.g.
New England Journal of Medicine).
Figure 6: Contribution of transitive closure diminishes for
large corpuses.
4 EXPERIMENTAL RESULTS
Traditional accuracy metrics for full text search and
web search are Precision and Recall (Baeza-Yates,
1999). Whereas the precision of semantic search is
good, the recall is expected to be somewhat poor in
comparison to full text search products, because we
follow transitive links to other documents.
For our tagging experiment, we used the social
tagging dataset culled from delicious that was used
in (Jiang, 2009). There are two versions of the TI
algorithm that we tested - the normal algorithm and
a filtered version (Filtered TI). The filtered version
takes the keywords produced by the TI and then
filters out keywords that do not appear in the
document a minimum number of times normalized
by the document length. We compare our results to
corpus dependent machine learning methods: KEA
(Witten, 1999), Linear Support Vector Machine
(SVM) and Ranking Support Vector Machine
(Ranking SVM) (Jiang, 2009). We used the same
parameter settings, test/training splits, etc. as (Jiang,
2009), for consistency. We also compare our results
to the standard Term Frequency (TF) and TFIDF
methods. Table 1 shows our results based on the
Precision at 5 (P @ 5) and Precision at 10 (P @ 10)
metrics.
The results are quite promising. Without
filtering, TI produces results that are approximate to
TFIDF, but in a corpus independent way. Once we
filter TI, we achieve results that surpass TF and
TFIDF and, in fact, are closing in on KEA. The
advantage is that our method scales linearly. One
interesting result is that TF performed better than
TFIDF, which could be due to the small corpus size
(600). Overall, the results show that TI provides a
solid foundation upon which DSI can be built.
Table 1: Precision results for our algorithm (TI and
Filtered TI) compared to others.
P @ 5 P @ 10
TI 0.289 0.221
TFIDF 0.295 0.23
TF 0.34 0.267
Filtered TI 0.38 0.27
KEA 0.437 0.31
SVM 0.469 0.323
Ranking SVM 0.495 0.349
For document similarity precision performance,
we constructed a corpus of 2500 documents scraped
from Wikipedia. The corpus consisted of 25 topics,
each with 100 documents each. Sample topics
include “american actors”, “american singers”, and
“national football league players”. Note, some of the
documents belonged in two categories, such as an
actor that was also a singer. This negatively affects
precision results for all methods including DSI. To
test the precision, we took a single document from
each of the topics and used it as the query document,
and then we obtained the top 10 most similar
SEMANTIC MINING OF DOCUMENTS IN A RELATIONAL DATABASE
155
documents. Then precision numbers at 1, 3, 5, and
10 were calculated. We compared our results to the
traditional Cosine similarity measure (CosSim)
based on TFIDF (Baeza-Yates, 1999).
The results in Table 2 show that DSI provides a
similar precision level to CosSim, but does so in
linear time instead of in O(N
2
) time, and is
completely corpus independent, unlike CosSim.
This is a huge win for customers whose workloads
are in the millions of documents, anything other than
linear will simply not be feasible at such scale.
Table 2: Precision results for DSI and CosSim.
P @ 1 P @ 3 P @ 5 P @ 10
DSI 0.8 0.8 0.79 0.78
CosSim 0.8 0.82 0.83 0.82
Figure 7 shows how FTI, TI and DSI mining
stack up in terms of end-to-end execution time (i.e.
sum total of computing all three indexes) on a real
customer workload sampled at 200k document
increments, with an average sample size of 40KB
per document in plain text format. The test machine
had 32GB of RAM and a DOP (degree of
parallelism) of 32. The results clearly show linear
scaling.
Figure 7: Total execution time (sec.) vs. Docs mined.
4.1 Incremental DSI Algorithm
Performance
As the corpus evolves over time (new documents are
added, and old ones are updated), the incremental
algorithm keeps the index fresh in an efficient
manner. However, there are a few expensive
operations involved in “back updates”. These are, in
increasing order of cost: 1) Lookup to find if cand
j
is
in the new (incremental) batch or not. For this we
can use an in-memory hash table; 2) Lookup to find
the weakest of the top K stored similarities for cand
j
;
and 3) Update (or delete followed by insert) in case
we need to update the weakest similarity for cand
j
.
This is the most expensive operation.
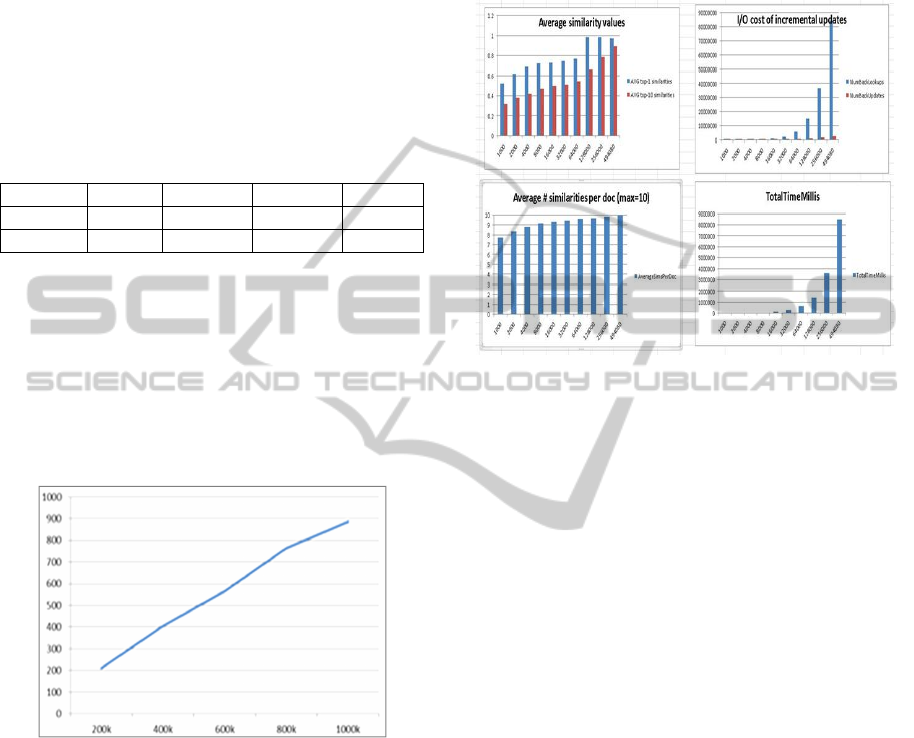
In Figure 8, we report on the accuracy and I/O
cost for various corpus sizes, from 1000 to ~500,000
documents (number of docs is on the X-axis).
Figure 8: Cost of incremental DSI.
One conclusion from the above analysis is that
the “average similarity values” (top left plot) shows
that the DSI approach gives quite good accuracy: we
will not have 100% accuracy (compared to some
“perfect similarity oracle”), but the fact that top-1
similarities, especially for large corpus sizes, are
close to 1 means that strong similarities are easily
identified; also, average top-10 similarities grow
nicely. The reason that those numbers (both for top-
1 and top-10) are lower for smaller size corpuses is
due to the fact that the lower the corpus size, the
lower the probability to find similar documents.
Secondly, the total time in milliseconds (lower-
right) graph shows that the runtime is linear: as we
double the document set size, the runtime roughly
doubles. Thirdly, the “I/O cost of incremental
updates” (upper-right) graph is similar to the
TotalTimeMillis one, in the sense that the number of
back-lookups and back-updates doubles when we
double the corpus size.
Another piece of learning from the above
analysis is that accuracy can benefit from the same
approach (back-updates) even for in-batch
documents. The reason is that back-updates act to
boost accuracy, and give some documents that may
have been missed by the candidate selection
heuristic a second chance. Given the high overhead
in I/O cost, we should be cautious to use this in all
cases, and we recommend to only using it for batch
updates, where this is absolutely needed, and to let
the non-incremental case run as fast as possible.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
156

The semantic mining algorithms have been
distributed in the form of SQL Server’s community
tech preview (CTP) bits, and have been well
received, with one Microsoft internal and one
external customer showing intent to adopt.
5 APPLICATIONS
With the search user experience, we have been used
to a document-centric rather than concept-centric
navigation of information. The overall
search/browse experience is somewhat broken at the
Enterprise (which is the primary concern of SQL
Server’s user base), because Enterprise documents
could be hundreds of pages long, and there may be
millions of documents in the repository, e.g.
SharePoint. People simply don’t have the time to
scan so much information and ultimately navigate to
the exact point of interest.
Based on mining the Phrase Similarity Index
(Section 3.4), we propose to enable a set of concept-
centric information navigation experiences (Figure
9). This enables the user to browse a document
collection by following links through concepts,
rather than through document names or a sequence
of search queries – especially useful in large
document collections where individual documents
are large, e.g. at the Enterprise. In Figure 10, we
show how the semantic graph may be used to
enhance the Windows Explorer user experience.
Figure 9: Exploring a concept graph.
Figure 10: Exploring mined concepts in a file system.
When a concept is browsed on the left, corresponding files
are highlighted on the right.
6 CONCLUSIONS
We have described the semantic mining algorithms
that lie at the core of Semantic Platform, which is
being released in the next version of SQL Server,
and shown that they scale linearly with large
document corpuses. The combination of the four
indexes facilitates the process and work flow of
browsing, searching and researching information at
the Enterprise, where documents can be large
compared to web pages. It also enables new and
intuitive user experiences along the lines of
browsing concepts that are contained in documents
instead of the documents themselves, e.g. using
filenames.
Future work includes keyword precision
improvements for the TI by utilizing additional
corpus independent features such as first occurrence
and phrase distribution (Jiang, 2009). Additionally,
for the DSI, exploring different candidate document
selection strategies and document similarity
functions are fruitful avenues of research that could
potentially yield gains in performance and precision.
We also plan to expose more tuning knobs (e.g. K
and K′ in Section 3.3) to better control the degree of
completeness of DSI results, and/or to adapt them as
the mining proceeds. Adaptive language modelling
is yet another promising future direction when
mining Enterprise document corpuses.
SEMANTIC MINING OF DOCUMENTS IN A RELATIONAL DATABASE
157

REFERENCES
Administering Full Text Search (http://msdn.microsoft.
com/en-us/library/ms142557.aspx).
Baeza-Yates, R., Ribeiro-Neto, B., Modern Information
Retrieval, Addison-Wesley, 1999.
Blei, D. M., Ng, A. Y., Jordan, M., Latent Dirichlet
allocation, Journal of Machine Learning Research No.
3, pp. 993 – 1022, 2003.
Cohen, J. D., Highlights: Language- and domain
independent automatic indexing terms for abstracting,
Journal of the American Society of Information
Science, Volume 46, Issue 3, pp. 162-174, April 1995.
Damashek, M., Gauging similarity with N-grams:
Language-independent categorization of text, Science
267, Feb. 1995.
Deerwester, S., et al., Improving Information Retrieval
with Latent Semantic Indexing, Proceedings of the
51st Annual Meeting of the American Society for
Information Science 25, 1988, pp. 36–40.
Full Text Search Overview (http://msdn.microsoft.com/en-
us/library/ms142571.aspx).
Gabrilovich, E., Markovitch, S., Computing semantic
relatedness using Wikipedia-based explicit semantic
analysis, in Proceedings of the 20
th
International Joint
Conference on Artificial Intelligence, 2007.
Hammouda, K., M., Kamel, M., S., Document Similarity
using a Phrase Indexing Graph Model, Journal of
Knowledge and Information Systems, Vol. 6, Issue 6,
November 2004.
Hofmann, T., “Probabilistic Latent Semantic Indexing”,
Proc. SIGIR, 1999.
Jiang, X., Hu, Y., Li, H., A Ranking Approach to
Keyphrase Extraction, Microsoft Research Technical
Report, 2009.
McNabb, K., Moore, C., and Levitt, D., Open Text Leads
ECM Suite Pure Plays, The Forrester Wave Vendor
Summary, Q4 2007.
Salton, G., Wong, A., Yang, C. S., “A Vector Space
Model for Automatic Indexing”, Communications of
the ACM, vol. 18, nr. 11, pages 613-620, 1975.
Silberschatz, A., Stonebraker, M., and Ullman, J.,
Database Research: Achievements and Opportunities
into the 21
st
Century. Technical Report, Stanford,
1996.
Tan, P-N., Steinbach, M., Kumar, V., Introduction to Data
Mining, 2005
Witten, I. H., Paynter, G. W., Frank, E., Gutwin, C., and
Nevill-Manning, C., G., KEA: Practical automatic
keyphrase extraction, Proc. DL ’99, pp. 254-256.
Zamir, O., Etzioni, O., Web Document Clustering: A
Feasibility Demonstration, in Proc. ACM SIGIR’98,
1998.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
158
