WIKIPEDIA AS DOMAIN KNOWLEDGE NETWORKS

Domain Extraction and Statistical Measurement

Zheng Fang

, Jie Wang

, Benyuan Liu

and Weibo Gong

Department of Computer Science, University of Massachusetts, Lowell, MA, U.S.A.

Department of Electrical and Computer Engineering, University of Massachusetts, Amherst, MA, U.S.A.

Keywords:

Knowledge network, Statistics, Power law, Degree distribution, Betweenness centrality, Clustering coefﬁcient,

Wikipedia, MathWorld.

Abstract:

This paper investigates knowledge networks of speciﬁc domains extracted from Wikipedia and performs sta-

tistical measurements to selected domains. In particular, we ﬁrst present an efﬁcient method to extract a

speciﬁc domain knowledge network from Wikipedia. We then extract four domain networks on, respectively,

mathematics, physics, biology, and chemistry. We compare the mathematics domain network extracted from

Wikipedia with MathWorld, the web’s most extensive mathematical resource created and maintained by pro-

fessional mathematicians, and show that they are statistically similar to each other. This indicates that Math-

World and Wikipedia’s mathematics domain knowledge share a similar internal structure. Such information

may be useful for investigating knowledge networks.

1 INTRODUCTION

Wikipedia, created a decade ago, has developed and

evolved rapidly into the most comprehensive online

encyclopedia. While people enjoy using it, their con-

cerns about the credibility of Wikipedia as an accurate

knowledge source linger on, which has triggered ex-

tensive research in recent years.

A body of knowledge may be viewed as a net-

work, where nodes in the network represent concepts

and tools, and edges between nodes represent the re-

lationship between them. The measurement of ma-

tureness of a speciﬁc knowledge network should in-

clude measures of accuracy and completeness. How-

ever, there has been no efﬁcient algorithm to evalu-

ate these two essential properties. A viable alterna-

tive would be to compare statistical properties of the

target knowledge network with a trusted knowledge

source, such as paper-based encyclopedia. Restricted

by weight and volume, however, paper-based ency-

clopedias cannot be truly comprehensive for measur-

ing completeness.

MathWorld, the web’s most extensive mathemati-

cal resource created and maintained by professional

mathematicians, matches the scale of Wikipedia’s

domain on mathematics and provides an excellent

trusted source as a base for comparison with the math-

ematics knowledge network contained in Wikipedia.

To carry out the comparison we must ﬁrst extract

the mathematics network contained in Wikipedia. In

particular, we will need to devise an effective mech-

anism to extract a knowledge network in a speciﬁc

domain from Wikipedia. To this end we devise a

three-step method to extract a speciﬁc knowledge net-

work from Wikipedia with high quality. We use

this method to extract four domain knowledge net-

works from Wikipedia on, respectively, mathematics,

physics, biology,and chemistry. We will refer to these

networks as, respectively, Wikipedia Math, Wikipedia

Physics, Wikipedia Biology, and Wikipedia Chem-

istry. We then carry out statistical analysis on these

four knowledge networks.

We show that Wikipedia Math and MathWorld

have similar statistical properties, which suggest that

the MathWorld and Wikipedia Math share a similar

internal structure. Such information may be served

as supporting evidence and necessary condition for

Wikipedia Math to be mature. While the compari-

son is on the mathematics domain, it still provides

a strong indication that other domains in Wikipedia

would also share such similarity with corresponding

professionally maintained sources, for the contribu-

tors of Wikipedia are volunteers from all areaswith no

particular quality preference on the mathematics do-

main. The measurement of statistical similarity may

be useful for investigating knowledge networks in ad-

159

Fang Z., Wang J., Liu B. and Gong W..

WIKIPEDIA AS DOMAIN KNOWLEDGE NETWORKS - Domain Extraction and Statistical Measurement.

DOI: 10.5220/0003633001510157

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 151-157

ISBN: 978-989-8425-79-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

dition to directly measuring accuracy and complete-

ness.

The rest of the paper is organized as follows. Sec-

tion 2 brieﬂy reviewspreviouswork on measuring and

analyzing Wikipedia. Section 3 presents a three-step

method to extract from Wikipedia a speciﬁc domain

knowledge network, and compares Wikipedia Math

with MathWorld. Section 4 concludes the paper.

2 RELATED WORK

Early attempts to measure Wikipedia, started in 2004,

were focused on content accuracy and reputation (Lih,

2004; Giles, 2005; Chesney, 2006). Most of these at-

tempts were centered on the metrics of content cor-

rectness and quality, not on the completeness of the

topics covered. For example, Voss (Voss, 2005) per-

formed statistical analysis on all available language

versions of Wikipedia. He examined a number of ar-

ticles and the growth rate in each available language

version of Wikipedia. Halavais and Lackaff (Halavais

and Lackaff, 2008) analyzed the diversity of the con-

tent of Wikipedia. They selected a number of topics

in paper-based encyclopedia and matched them with

those in Wikipedia. They concluded that Wikipedia is

indeed diversiﬁed in its content coverage.

Other work has focused on the relationship be-

tween collaborativeeditingand content quality (Zlati´c

et al., 2006; Kittur and Kraut, 2008). These studies in-

dicated that in the online collaboration environment,

the quality of the content can be improved through

cooperation of multiple contributors over time, and

coordination can lead to better quality. However,

there has been no direct evidence provided to mea-

sure the quality of the content currently presented in

Wikipedia.

While most of the research treats Wikipedia as

one complex network, a number of authors have in-

vestigated the hierarchical structure of Wikipedia.

For example, Muchnik et al (Muchnik et al., 2007)

studied how to automatically discover hierarchies in

Wikipedia, Yu et al (Yu et al., 2007) studied how

to evaluate ontology with Wikipedia categories, and

Silva et al (Silva et al., 2010) studied how to identify

borders of certain knowledge networks.

Previous analysis of degree distributions in

Wikipedia were focused on the entire Wikipedia,

which concluded that the Wikipedia’s degree distri-

bution follows the power law, the same as that of the

World Wide Web (Voss, 2005; Capocci, 2006; Kamps

and Koolen, 2009).

3 STATISTICAL MEASUREMENT

OF WIKIPEDIA

In the case when there exists a trusted mature knowl-

edge network of a certain domain, measuring the

same domain knowledge networks extracted from

Wikipedia can be carried out by comparing the topic

coverage and the statistical structures of the two net-

works. The growth of online resources has provided

trusted domain-speciﬁc knowledge that could match

the scale of Wikipedia in the same domain. For ex-

ample, MathWorld, produced by Wolfram Research,

is a reliable and extensive resource on the knowledge

of mathematics. It was created and has been main-

tained by a group of mathematicians and related pro-

fessionals for over a decade, and is therefore viewed

as a mature knowledge network on mathematics. The

existence of MathWorld allows us to compare the ma-

tureness of Wikipedia.

3.1 Extraction of a Speciﬁc Domain

Knowledge Network

The richness of content presented in Wikipedia, while

being the reason for the popularity of Wikipedia, also

makes it difﬁcult to extract a speciﬁc knowledge do-

main, for the boundaries between domains are blurry

as people keep pushing the fringes and adding more

materials.

To extract a certain domain knowledge network

from Wikipedia, e.g chemistry, an ideal approach

would be to ﬁnd a complete list of unambigu-

ous chemistry terminologies (this list should con-

tain words of all named reactions and named com-

pounds, among other things), extract all Wikipedia

pages whose titles match the words in the list, and

rebuild links between these pages. Commonly used

chemistry dictionaries would help, but not sufﬁcient,

since the completeness and unambiguity are hardly

guaranteed (e.g. mercury as a chemical element vs.

mercury as a planet).

Page tracing is an effective alternative to building

the chemistry knowledge network from Wikipedia.

That is, starting from the main chemistry page, titled

“Chemistry”, we follow all the links presented in this

page to include new pages to the network, and do so

recursively until no new pages are found. Note that it

is quite often that a link from a page in the domain of

chemistry will lead to a page in a completely differ-

ent domain. Therefore, appropriate ﬁlters should be

applied to examine the links to ensure that the linked

pages are still in the scope of chemistry.

Filters may be a keyword-based pass ﬁlter or

a keyword-based block ﬁlter. Given a set of pre-

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

160

determined keywords in a speciﬁc domain, a pass ﬁl-

ter passes a page if the page title matches or contains

one of these keywords, and blocks it otherwise. Given

a set of pre-determined keywords not in the given do-

main, a block ﬁlter blocks a page if the title of the

page matches or contains one of the keywords, and

passes it otherwise. Constructing either type of ﬁl-

ters, however, is challenging, for it is difﬁculty to

predict what kind of keywords will appear or not ap-

pear in the title of a page and the outgoing link could

point to a completely different and unexpected cate-

gory. In particular, an overstrict pass ﬁlter may fail

to include pages that should be included, while an in-

sufﬁcient block ﬁlter may include pages that should

not be included. There is another major drawback in

page tracing: It may fail to discover pages that are

not reachable from other pages. Such “hidden” pages

may be newly created pages that have not been linked

to from any existing page, pages that contain fringe

topics known to only a small number of people, or

pages that consist of rarely used organic compounds

in chemistry.

To overcome these drawbacks, we devise an effec-

tive method to extract a domain knowledge network

from Wikipedia based on page titles and page cate-

gories. The page category, a feature of Wikipedia,

is used to classify pages. Each page belongs to one

or more categories and each category contains several

pages or sub-categories. The categories of a page can

be found at the end of the page, and the category itself

can be viewed as a special page. Although typically

hidden from the user, the category information can

be obtained by explicitly loading the page with the

“Category:” preﬁx. We use page categories to gen-

erate new pages and check whether a page should be

included in the network. Our extraction mechanism

consists of the following three steps.

Step 1: Extract Domain Category Hierarchy.

Each category may contain a number of pages or sub-

categories, thus categories themselves could form a

hierarchy, representing a framework of the domain

knowledge. We use page categories to generate new

pages in this step.

An ideal domain hierarchy should be a directed

acyclic graph containing exactly those nodes in the

domain, but the Wikipedia categoryhierarchies are far

from being ideal. In particular, a category hierarchy

may contain two types of loops. They are local loops

and out-domain loops. By local loops it means that

two or more closely related categories (sometimes

they are actually the same but with slightly different

categorical descriptions)contain each other. This type

of loops has no important effecton the domain knowl-

edge generation. By out-domain loops it means loops

containing a node in a different domain. Out-domain

loops could be catastrophic if not handled properly,

for they might lead to a super-category that contains

chemistry as a subcategory. Take the following out-

domain loop as an example:

Chemistry → ··· → Silicon → ··· → Memory →

Knowledge → Science → ··· → Chemistry

where the ambiguity of “Memory” leads to a misin-

terpretation as human memory instead of computer

memory as it is intended to be, which in turn leads to

the super-category of “Knowledge” of human knowl-

edge. If such out-domain loop is not handled prop-

erly, all categories under “Knowledge” would be in-

cluded. Fortunately, such out-domain loops are rare,

as the category misclassiﬁcation errors are reported

by users everyday, and Wikipedia editors correct such

errors efﬁciently.

Deploying keyword-based block ﬁlters can avoid

such misinterpretations by properly selecting a set of

keywords. We repeat the process of generating the

domain category hierarchy several times and update

the block ﬁlter accordingly until a satisfactory quality

is obtained.

Step 2: Extract Pages. With the hierarchy of do-

main categories at hand, we are ready to extract pages

that belong to the hierarchy. We note that some pages

listed under a category in the hierarchy may not be-

long to the domain of interest and should not be in-

cluded. For example, a biography of a chemist might

be listed in the hierarchy and should not be included

in the Wikipedia Chemistry network. The category

information of a page can be used to check for in-

clusion. Since a page might belong to several dif-

ferent categories, the page which should not be in-

cluded would contain keyword in the titles of its con-

catenated categories. For instance, chemists also be-

long to the category of “People”. To avoid adding

chemists into our knowledge network, we can simply

add a keyword “People” to the block ﬁlter. Other sim-

ilar block-keywords would be “Birth”, “Prize”, and

“Facility”, to name only a few.

After extracting pages that pass the block ﬁlter, we

scan each page for linkage and build links within the

current set of pages. No new pages will be included

at this point.

Step 3: Trim Disconnected Component. Note that

certain pages in the network after the previous two

steps might belong to a cluster that are disconnected

from any other node in the network. This can be used

WIKIPEDIA AS DOMAIN KNOWLEDGE NETWORKS - Domain Extraction and Statistical Measurement

161

to remove further unwanted pages that are still con-

tained in the category hierarchy. Intuitively, the mis-

classiﬁed categories will generate its own pages that

clustered together, but with no links to the target do-

main. For example, the “metal music genre”, which is

misclassiﬁed as a subcategory of “metal” and passes

the block ﬁlter, will generate pages such as “history

of metal music”, “metal music band”, “songs”, and

other things. But none of these pages has links to the

chemistry knowledge network. Removing the largest

connected component of such pages, we will have a

network of higher quality with less noise.

Remark. Theoretically it may be possible to have

disconnected components that contain the wanted

domain knowledge. But such phenomena never

happened in our experiments. This makes sense, for

the real-world domain knowledge networks probably

do not work that way. It is hard to imagine that within

the same domain there are parts that are completely

isolated from each other. We also note that, although

the data set we extracted from Wikipedia may still

contain misclassiﬁed nodes, the fraction of these

nodes is very small. Thus, any negative effect there

is to the accuracy of statistical analysis will be small

and can be safely ignored.

We present four domain knowledge networks ex-

tracted from Wikipedia using our three-step method.

They are Wikipedia Math, Wikipedia Physics,

Wikipedia Biology, and Wikipedia Chemistry. Ta-

ble 1 shows the number of nodes and edges for each

of these networks.

Table 1: Wikipedia four domains statistics.

Math Phys Bio Chem

Nodes 18,673 16,132 162,726 39,674

Edges 295,772 206,878 2,526,351 1,677,833

3.2 Comparison of Wikipedia Math

with MathWorld

We compare Wikipedia Math with MathWorld on de-

gree distribution, betweenness centrality, and cluster-

ing coefﬁcients. Jia et al (Jia and Guo, 2009) provided

the statistical analysis of MathWorld, which will serve

as the base of our comparison.

3.2.1 Degree Distribution

The MathWorld network studied in (Jia and Guo,

2009) contains over 12,000 entries as on December

1st, 2008 (MathWorld currently contains 13,067 en-

tries as on May 3rd, 2011). The degree distributions

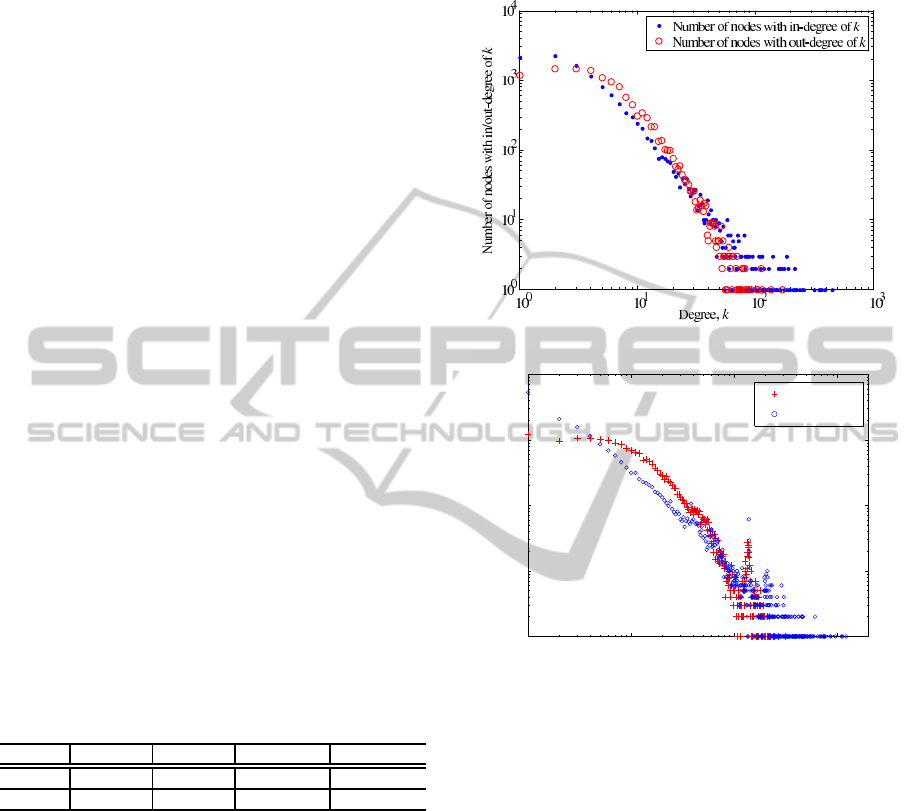
of MathWorld and Wikipedia Math are plotted in Fig-

ure 1.

(a) MathWorld (Jia and Guo, 2009).

Degree

Number of ndoes

out−degree

in−degree

(b) Wikipedia Math.

Figure 1: Degree distribution of MathWorld and Wikipedia

Math.

It can be seen from the degree plots that both in-

degree and out-degree distributions between Math-

World and Wikipedia Math are very similar, and ex-

hibits power-law behavior. The data run short of the

heavy tail and drop downquickly at the end. This phe-

nomenon also happens in some other studies on the

power law, which is analyzed and discussed in (Gong

et al., 2005). In the Wikipedia Math plot, the ver-

tical feature around degree 100 implies that the data

set contains several ensemble pages (a.k.a. directory

pages) that serve as containers of a list of pages. For

instance, “outline of probability” and “NP-complete

problems” are container pages.

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

162

3.2.2 Betweenness Centrality

Betweenness centrality of node i is deﬁned by

bc(i) =

∑

j,k∈N,i6= j6=k

(i)

(1)

where n

denotes the number of shortest paths from

node j to node k and n

(i) is the number of presence

of i on the shortest paths. A node will have a large be-

tweenness centrality value if it connects a large num-

ber of nodes on their shortest paths. In a knowledge

network, the nodes of large betweenness centrality

would be considered as important fundamental con-

cepts in the knowledge network. The comparison of

betweenness centrality is shown in Figure 2.

(a) MathWorld (Jia and Guo, 2009).

0 5,000 10,000 15,000 20,000

x 10

Ordered node index

Betweenness centrality

(b) Wikipedia Math.

Figure 2: Betweenness centrality of MathWorld and

Wikipedia Math.

Most nodes in MathWorld and Wikipedia Math

have low betweenness centrality with a value less

than 1. Only a small portion of nodes have very

large betweenness centrality values. Table 2 lists

top ten highest betweenness centrality topics in

both MathWorld (Jia and Guo, 2009), Wikipedia

Math, Wikipedia Physics, Wikipedia Biology, and

Wikipedia Chemistry. The top ten topics in Wikipedia

Math approximately match those in MathWorld. This

suggests a similar set of core knowledge that play an

important role in connecting knowledge are shared

in both MathWorld and Wikipedia Math. The top-

ics with top 10 betweenness centrality in the rest of

the domains also match important concepts of each

domain.

3.2.3 Clustering Coefﬁcient

The clustering coefﬁcient of a node is a measure of

direct connectivity of its neighbors. There is ev-

idence suggests that in most real-world networks,

especially in social networks, nodes tend to create

tightly knit groups over those in randomly generated

networks (Holland and Leinhardt, 1971; Watts and

Strogatz, 1998). Therefore, the clustering coefﬁcient

may be used to discover hierarchies in a given net-

work (Watts and Strogatz, 1998). The measurement

of clustering coefﬁcient for node i in a directed graph

is deﬁned as follows (Caldarelli, 2007):

− 1)

∑

j,k

+ A

(2)

out

− 1)

∑

j,k

+ A

(3)

Where k

and k

out

denote, respectively, the in-degree

and out-degree of node i, and A

equals 1 if there

exists an edge from i to j, 0 otherwise.

The clustering coefﬁcients plotted against ordered

node indexes is shown in Figure 3. In MathWorld,

the average in-clustering and out-clustering coefﬁ-

cients reported are 0.2536 and 0.1980 (Jia and Guo,

2009), respectively, while in Wikipedia Math the cor-

responding numbers are 0.2324 and 0.2898. The in-

clustering coefﬁcient is similar but the out-clustering

coefﬁcient is slightly higher in Wikipedia Math. This

can be explained as follows: In Wikipedia Math, top-

ics are often elaborated in more details with more

references (i.e., with more outgoing links) to fun-

damental concepts used in the articles. Compare

with the theoretical value O(|N|

−1

) in random net-

works (8.3× 10

−5

for MathWorld and 5.4× 10

−5

for

Wikipedia Math), the average clustering coefﬁcients

in two mathematics networks are both substantially

larger by several order of magnitude, which indicate

that both networks contain a hierarchical structure.

WIKIPEDIA AS DOMAIN KNOWLEDGE NETWORKS - Domain Extraction and Statistical Measurement

163

Table 2: Top 10 topics with highest betweenness centrality.

MathWorld Math Physics Biology Chemistry

1 Circle Statistics Physics Animal Carbon

2 Polynomial Integer Hydrogen Plant Hydrogen

3 Binomial Coefﬁcient Function Refractive Insect Chemical Compound

4 Prime Number Topology Quantum Mechanics Arthropod NMR Spectroscopy

5 Integer Matrix Molecule Fungus Catalysis

6 Set Group Density Gene Infrared Spectroscopy

7 Matrix Vector Space Wavelength Protein Chemical Reaction

8 Group Number Theory General Relativity Enzyme Chemistry

9 Power Prime Number Temperature Lepidoptera Relative Permittivity

10 Graph Set Magnetic Field Bacteria Nucleotide

(a) MathWorld (Jia and Guo, 2009).

0 2,500 5,000 7,500 10,00012,50015,00017,50020,000

0.2

0.4

0.6

0.8

Ordered node index

Clustering coefficient

In−clustering

Out−clustering

(b) Wikipedia Math.

Figure 3: Clustering coefﬁcient in MathWorld and

Wikipedia Math.

3.3 From Mathematics to Other

Domains

The comparison results between MathWorld and

Wikipedia Math suggest that these two mathemati-

cal knowledge networks are statistically similar. This

matches the common impression of knowledge in

Wikipedia’s mathematical domain. Such statistical

similarity suggests that MathWorld and Wikipedia

Math share a similar internal structure, which may be

served as supporting evidence and necessary condi-

tion to measure the matureness of Wikipedia Math.

It would be more comprehensiveto compare other

domain knowledge networks with corresponding pro-

fessionally maintained sources of the same domain as

well. However, such sources rarely exist and if any,

is hard to obtain. Nevertheless, although our compar-

ison is only based on the domain of mathematics, it

still provides a strong indication that other domains

in Wikipedia would also share the statistical simi-

larity with corresponding professionally maintained

sources, for the contributors of Wikipedia are from

all areas and have no preference of particular quality

on the domain of mathematics.

4 CONCLUSIONS

Measuring Wikipedia and studying its properties as

a comprehensive human knowledge network have at-

tracted much attention in knowledge discovery and

complex system. In this paper we compare Wikipedia

Math with MathWorld from a statistical point of view,

and conclude that Wikipedia Math is statistically sim-

ilar to MathWorld.

To compare Wikipedia’s domain knowledge net-

works, we devise an efﬁcient three-step method to ex-

tract domain knowledge with high quality. Four do-

main knowledge networks on mathematics, physics,

biology, and chemistry are extracted from Wikipedia.

Our experiments demonstrate the effectiveness of the

proposed method. Statistical analysis are carried out

on the four domains knowledge networks.

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

164

ACKNOWLEDGEMENTS

The ﬁrst author was supported in part by the NSF un-

der grant CCF-0830314. The second author was sup-

ported in part by the NSF under grants CCF-0830314,

CNS-0958477, and CNS-1018422. The third author

was supported in part by the NSF under grants CNS-

0721626, CNS-0953620, and CNS-1018303. The

fourth author was supported in part by NSF under

grant EFRI-0735974 and by the Army Research Of-

ﬁce under Contract W911NF-08-1-0233.

The authors thank Xu Yuan for his help on the

early stage of knowledge network extractions.

REFERENCES

Caldarelli, G. (2007). Scale-Free Network. Oxford Uni-

veristy Press.

Capocci, A. (2006). Preferential attachment in the

growth of social networks: The internet encyclopedia

wikipedia”. Phys. Rev. E; Physical Review E, 74(3).

Chesney, T. (2006). An empirical examination of

wikipedia’s credibility. Firstmonday, 11.

Giles, J. (2005). Internet encyclopaedias go head to head.

Nature, 438(7070):900–901.

Gong, W., Liu, Y., Misra, V., and Towsley, D. F. (2005).

Self-similarity and long range dependence on the in-

ternet: a second look at the evidence, origins and im-

plications. Computer Networks, 48(3):377–399.

Halavais, A. and Lackaff, D. (2008). An analysis of top-

ical coverage of wikipedia. Journal of Computer-

Mediated Communication, 13(2):429–440.

Holland, P. W. and Leinhardt, S. (1971). Transitivity

in structural models of small groups. Comparative

Group Studies, 2(2):107–124.

Jia, Q. and Guo, Y. (2009). Discovering the knowledge hi-

erarchy of mathworld for web intelligence. In Fuzzy

Systems and Knowledge Discovery, 2009. FSKD ’09.

Sixth International Conference on, volume 7, pages

535 –539.

Kamps, J. and Koolen, M. (2009). Is wikipedia link struc-

ture different? In Proceedings of the Second ACM

International Conference on Web Search and Data

Mining, WSDM ’09, pages 232–241, New York, NY,

USA. ACM.

Kittur, A. and Kraut, R. E. (2008). Harnessing the wisdom

of crowds in wikipedia: quality through coordination.

In Proceedings of the 2008 ACM conference on Com-

puter supported cooperative work, CSCW ’08, pages

37–46, New York, NY, USA. ACM.

Lih, A. (2004). Wikipedia as participatory journalism: Re-

liable sources? metrics for evaluating collaborative

media as a news resource. Proceedings of the Inter-

national Symposium on Online Journalism 2004.

Muchnik, L., Itzhack, R., Solomon, S., and Louzoun, Y.

(2007). Self-emergence of knowledge trees: Extrac-

tion of the wikipedia hierarchies. Physical Review

E (Statistical, Nonlinear, and Soft Matter Physics),

76(1).

Silva, F. N., Travencolo, B. A., Viana, M. P., and da Fon-

toura Costa, L. (2010). Identifying the borders of

mathematical knowledge. Journal of Physics A:

Methematical and Theoretical, 43(325202).

Voss, J. (2005). Measuring wikipedia. In Proceedings of

the 10th International Conference of the International

Society for Scientometrics and Informetrics.

Watts, D. and Strogatz, S. (1998). Collective dynamics of

small-world networks. Nature, 393(6684):440–442.

Yu, J., Thom, J. A., and Tam, A. (2007). Ontology eval-

uation using wikipedia categories for browsing. In

Proceedings of the sixteenth ACM conference on Con-

ference on information and knowledge management,

CIKM ’07, pages 223–232, New York, NY, USA.

ACM.

Zlati´c, V., Boˇziˇcevi´c, M.,

Stefanˇci´c, H., and Domazet, M.

(2006). Wikipedias: Collaborative web-based ency-

clopedias as complex networks. Physical Review E,

74(1):016115.

WIKIPEDIA AS DOMAIN KNOWLEDGE NETWORKS - Domain Extraction and Statistical Measurement

165