
A TWO-WAY APPROACH FOR PROBABILISTIC GRAPHICAL
MODELS STRUCTURE LEARNING AND ONTOLOGY
ENRICHMENT
Mouna Ben Ishak
1
, Philippe Leray
2
and Nahla Ben Amor
1
1
LARODEC Laboratory, ISG, University of Tunis, 2000 Tunis, Tunisia
2
Knowledge and Decision Team, LINA Laboratory UMR 6241, Polytech’Nantes, Nantes, France
Keywords:
Ontologies, Probabilistic graphical models (PGMs), Machine learning, Ontology enrichment.
Abstract:
Ontologies and probabilistic graphical models are considered within the most efficient frameworks in knowl-
edge representation. Ontologies are the key concept in semantic technology whose use is increasingly preva-
lent by the computer science community. They provide a structured representation of knowledge characterized
by its semantic richness. Probabilistic Graphical Models (PGMs) are powerful tools for representing and rea-
soning under uncertainty. Nevertheless, both suffer from their building phase. It is well known that learning
the structure of a PGM and automatic ontology enrichment are very hard problems. Therefore, several algo-
rithms have been proposed for learning the PGMs structure from data and several others have led to automate
the process of ontologies enrichment. However, there was not a real collaboration between these two research
directions. In this work, we propose a two-way approach that allows PGMs and ontologies cooperation. More
precisely, we propose to harness ontologies representation capabilities in order to enrich the building process
of PGMs. We are in particular interested in object oriented Bayesian networks (OOBNs) which are an ex-
tension of standard Bayesian networks (BNs) using the object paradigm. We first generate a prior OOBN
by morphing an ontology related to the problem under study and then, we describe how the learning process
carried out with the OOBN might be a potential solution to enrich the ontology used initially.
1 INTRODUCTION
Ontologies are the key concept in semantic web, they
allow logical reasoning about concepts linked by se-
mantic relations within a knowledge domain. Prob-
abilistic graphical models (PGMs), from their side,
provide an efficient framework for knowledge rep-
resentation and reasoning under uncertainty. Even
though they represent two different paradigms, On-
tologies and PGMs share several similarities which
has led to some research directions aiming to combine
them. In this area, Bayesian networks (BNs) (Pearl,
1988) are the most commonly used. However, given
the restrictive expressiveness of BNs, proposed meth-
ods focus on a restrained range of ontologies and ne-
glect some of their components. To overcome this
weakness, we propose to explore other PGMs, signif-
icantly more expressive than standard BNs, in order
to address an extended range of ontologies.
We are in particular interested in object oriented
Bayesian networks (Bangsø and Wuillemin, 2000)
(OOBN), which are an extension of standard BNs.
In fact, OOBNs share several similarities with on-
tologies and they are suitable to represent hierarchi-
cal systems as they introduce several aspects of ob-
ject oriented modeling, such as inheritance. Our idea
is to define the common points and similarities be-
tween these two paradigms in order to set up a set of
mapping rules allowing us to generate a prior OOBN
by morphing ontology in hand and then to use it as a
starting point to the global OOBN learning algorithm,
this latter will take advantages from both semanti-
cal data, derived from ontology which will ensure its
good start-up and observational data. We then capi-
talize on the final structure resulting from the learning
process to carry out the ontology enrichment. By this
way, our approach ensures a real cooperation, in both
ways, between ontologies and OOBNs.
The remainder of this paper is organized as fol-
lows: In sections 2 and 3 we provide a brief represen-
tation of our working tools. In section 4, we introduce
our new approach. In section 5, we look over the re-
lated work. The final section summarizes conclusions
reached and outlines directions for future research.
189
Ben Ishak M., Leray P. and Ben Amor N..
A TWO-WAY APPROACH FOR PROBABILISTIC GRAPHICAL MODELS STRUCTURE LEARNING AND ONTOLOGY ENRICHMENT.
DOI: 10.5220/0003634801890194
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2011), pages 189-194
ISBN: 978-989-8425-80-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

2 ONTOLOGIES
For the AI community, an ontology is an explicit spec-
ification of a conceptualization (Gruber, 1993). That
is, an ontology is a description of a set of represen-
tational primitives with which to model an abstract
model of a knowledge domain. Formally, we define
an ontology O = hC p, R , I , A i as follows:
• C p = {cp
1
, . . . cp
n
} is the set of n concepts
(classes) such that each cp
i
has a set of k prop-
erties (attributes) P
i
= {p
1
, . . . p
k
}.
• R is the set of binary relations among elements of
C p which consists of two subsets:
– H
R
which describes the inheritance relations
among concepts.
– S
R
which describes semantic relations among
concepts. That is, each relation cp
i
s
R
cp
j
∈ S
R
has cp
i
as a domain and cp
j
as a range.
• I is the set of instances, representing the knowl-
edge base.
• A is the set of the axioms of the ontology. A con-
sists of constraints on the domain of the ontology
that involve C p, R and I .
During the last few years, increasing attention has
been focused on ontologies and ontological engineer-
ing. By ontological engineering we refer to the set
of activities that concern the ontology life cycle, cov-
ering its design, deployment, up to its maintenance
which is becoming more and more crucial to ensure
the continual update of the ontology toward possible
changes. The ontology evolution process (Stojanovic
et al., 2002) is defined as the timely adaptation of an
ontology in response to a certain change in the do-
main or its conceptualization. Evolution can be of
two types (Khattak et al., 2009):
• Ontology Population Process. consists in intro-
ducing new instances of the ontology concepts
and relations.
• Ontology Enrichment Process. consists in
adding (removing) concepts, properties and (or)
relations in the ontology or making some modi-
fications in the already existing ones because of
changes required in the ontology definition itself,
and then populate it for its instances. Ontology
enrichment techniques are automatic processes,
which generate a set of the possible modifications
on the ontology and propose these suggestions to
the ontology engineers.
This paper proposes to harness PGMs structure
definition in order to improve the process of ontolo-
gies enrichment. We are in particular interested in ob-
ject oriented Bayesian networks. Before introducing
our method, we give basic notions on this framework.
3 OBJECT ORIENTED BAYESIAN
NETWORKS
Probabilistic graphical models (PGMs) provide
an efficient framework for knowledge represen-
tation and reasoning under uncertainty. Ob-
ject oriented Bayesian networks (OOBNs) (Bangsø
and Wuillemin, 2000) (Koller and Pfeffer, 1997)
are an extension of standard Bayesian networks
(BNs) (Pearl, 1988) using the object paradigm. They
are a convenientrepresentation of knowledge contain-
ing repetitive structures. So they are a suitable tool to
represent some special relations which are not obvi-
ous to represent using standard BNs (e.g., examine
a hereditary character of a person given those of his
parents). Thus an OOBN models the domain using
fragments of a Bayesian network known as classes.
Each class can be instantiated several times within
the specification of another class. Formally, a class
T is a DAG over three, pairwise disjoint sets of nodes
(I
T
, H
T
, O
T
), such that for each instantiation t of T:
• I
T
is the set of input nodes. All input nodes are
references to nodes defined in other classes (called
referenced nodes).
• H
T
is the set of internal nodes including instan-
tiations of classes which do not contain instantia-
tions of T .
• O
T
is the set of output nodes. They are nodes from
the class usable outside the instantiations of the
class. An output node of an instantiation can be
a reference node if it is used as an output node of
the class containing it.
Internal nodes (expect classes instantiations) and
output nodes (except those which are reference nodes)
are considered as real nodes and they represent vari-
ables. In an OOBN, nodes are linked using either di-
rected links (i.e., links as in standard BNs) or refer-
ence links. The former are used to link reference or
real nodes to real nodes, the latter are used to link ref-
erence or real nodes to reference nodes. Each node
in the OOBN has its potential, i.e. a probability dis-
tribution over its states given its parents. To express
the fact that two nodes (or instantiations) are linked
in some manner, we can also use construction links
(− − −) which only represent a help to the specifica-
tion.
When some classes in the OOBN are similar (i.e.
share some nodes and potentials), their specification
KEOD 2011 - International Conference on Knowledge Engineering and Ontology Development
190
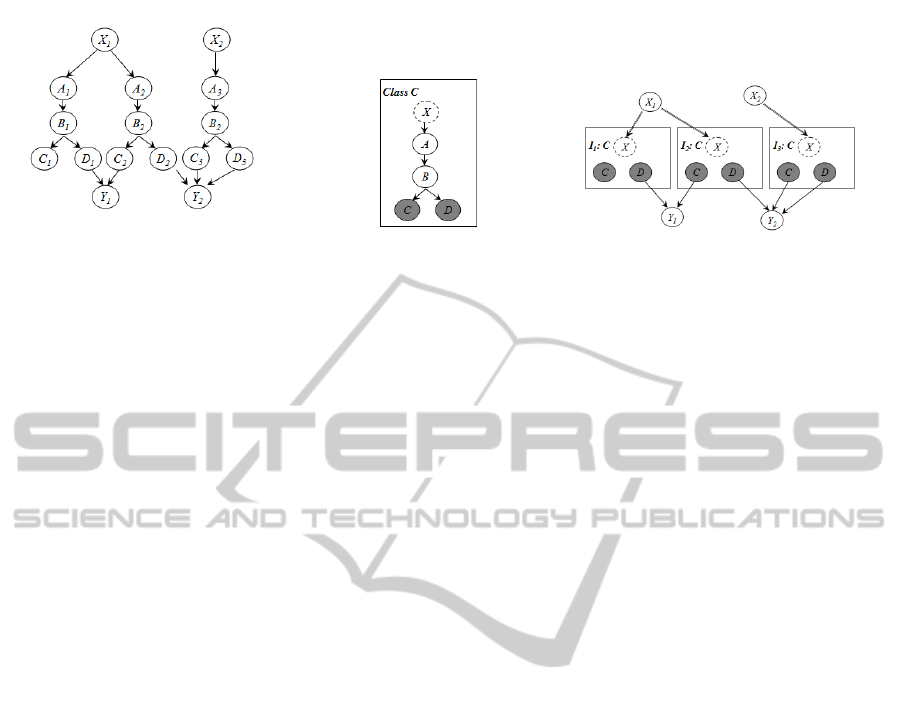
(a) The standard BN. (b) The class definition. (c) The OOBN representation.
Figure 1: An OOBN example.
can be simplified by creating a class hierarchy among
them. Formally, a class S over (I
S
, O
S
, H
S
) is a sub-
class of a class T over (I
T
, O
T
, H
T
), if I
T
⊆ I
S
, O
T
⊆
O
S
and H
T
⊆ H
S
.
In the extreme case where the OOBN consists of a
class having neither instantiations of other classes nor
input and output nodes we collapse to standard BNs.
Example 1. In figure 1, assume that in the BN of 1(a)
X
1
and X
2
have the same state space and the condi-
tional probability tables (CPTs) associated with all
nodes labeled A
i
as well as nodes labeled B
i
, C
i
and
D
i
, where i = {1, 2, 3} are identical. Hence, we have
three copies of a same structure. Thus, when model-
ing an OOBN such a repetitive structure will be pre-
sented by a class 1(b), where the dashed node X is
the input node (an artificial node having the same
state space as X
1
and X
2
), the shaded nodes C and
D are output nodes, and A and B are the encapsu-
lated nodes. Thus, we can represent the BN of figure
(a) using an OOBN model (c). The class C is instan-
tiated three times and the nodes X
1
, X
2
, Y
1
and Y
2
are
connected to the appropriate objects labeled I.1, I.2
and I.3.
4 A NEW APPROACH FOR
OOBN-ONTOLOGY
COOPERATION: 2OC
In this section, we expose our two-way approach that
integrates the ontological knowledge in the OOBN
learning process by morphing an ontology into a prior
OOBN structure then, the final structure derived from
the learning process is used to provide a set of possi-
ble extensions allowing the enrichment of the ontol-
ogy used initially.
4.1 The Morphing Process
We associate ontology concepts to classes of the
OOBN framework and concept properties to their sets
of random variables (real nodes). Concepts that are
connected by a subsumption relationship in the ontol-
ogy will be represented by a class hierarchy in the
prior OOBN, and semantic relations, which we as-
sume that they follow a causal orientation (Ben Ishak
et al., 2011), are used to specify classes interfaces and
instantiations organization in the OOBN.
To provide the morphing process, we assume that
the ontology conceptual graph is a directed graph
whose nodes are the concepts and relations (seman-
tic and hierarchical ones) are the edges. Our target
is to accomplish the mapping of this structure into
a prior OOBN structure while browsing each node
once and only once. To this end, we adapt the generic
Depth-First Search (DFS) algorithm for graph travers-
ing. The idea over the Depth-First Search algorithm is
to traverse a graph by exploring all the vertices reach-
able from a source vertex: If all its neighbors have al-
ready been visited (in general, color markers are used
to keep track), or there are no ones, then the algorithm
backtracks to the last vertex that had unvisited neigh-
bors. Once all reachable vertices have been visited,
the algorithm selects one of the remaining unvisited
vertices and continues the traversal. It finishes when
all vertices have been visited. The DFS traversal al-
lows us to classify edges into four classes that we use
to determine actions to do on each encountered con-
cept:
• Tree Edges: are edges in the DFS search tree.
They allow to define actions on concepts encoun-
tered for the first time.
• Back Edges: join a vertex to an ancestor already
visited. They allow cycle detection, in our case
these edges will never be encountered. As our
edges respect a causal orientation having a cycle
of the form X
1
→ X
2
→ X
3
→ X
1
means that X
1
is
A TWO-WAY APPROACH FOR PROBABILISTIC GRAPHICAL MODELS STRUCTURE LEARNING AND
ONTOLOGY ENRICHMENT
191

the cause of X
2
which is the cause of X
3
so this lat-
ter cannot be the cause of X
1
at the same instant t
but rather at an instant t + ε. We are limited to on-
tologies that do not contain cycles, because such
relationships invoke the dynamic aspect which is
not considered in this work.
• Forward and Cross Edges: all other edges. They
allow to define actions to do on concepts that are
already visited crossing another path and so hav-
ing more than one parent.
A deep study of the similarities between on-
tologies and the OOBN framework and a more de-
tailed description of the morphing process can be find
in (Ben Ishak et al., 2011).
4.2 The Learning Process
Few works have been proposed in the literature to
learn the structure (Bangsø et al., 2001) (Langseth
and Nielsen, 2003) of an OOBN. (Langseth and
Nielsen, 2003) proposed the OO-SEM algorithm
which consists of two steps. First, they take advan-
tages from prior information available when learn-
ing in object oriented domains. Thus, an expert is
asked about a partial specification of an OOBN by
grouping nodes into instantiations and instantiations
into classes. Having this prior model, the second
step starts by learning the interfaces of the instanti-
ations. Then, the structure inside each class is learned
based on the candidate interfaces founded previously.
Thanks to the morphing process described above, we
are not in need of expert elicitation as our process al-
lowed us to take advantage of the semantic richness
provided by ontologies to generate the prior OOBN
structure. This later will be used as a starting point
to the second step which will be done as described
in (Langseth and Nielsen, 2003).
4.3 The Change Detection Process
To get the final OOBN structure we have gathered
both ontology semantic richness and observational
data. Yet, in some cases, data may contradict the on-
tological knowledge which leads us to distinguish two
possible working assumptions:
• A Total Confidence in the Ontology. Any con-
tradiction encountered during the learning pro-
cess is due to data. The conflict must be man-
aged while remaining consistent with the onto-
logical knowledge. The enrichment process will
be restrained to the addition of certain knowledge
(relations, concepts, etc.) while preserving the
already existing ones and what was regarded as
truth remains truth.
• A Total Confidence in the Data. Any contra-
diction encountered during the learning process is
due to the ontology. The conflict must be man-
aged while remaining faithful to the data. In
this case, changing the conceptualization of the
ontology will be allowed, not only by adding
knowledge, but also by performing other possi-
ble changes, such as deleting, merging, etc. This
means that the data will allow us to get new truths
that may suspect the former. In the following we
will adopt this assumption.
As described above, the OO-SEM algorithm starts
by learning the interface of each class then learns the
structure inside each class. We can benefit of these
two steps in order to improve the ontology granular-
ity. In fact, the first step allows us to detect the possi-
ble existence of new relations and / or concepts which
might be added to the ontology at hand. The second
step may affect the definition of the already existing
concepts and / or relations.
4.3.1 Interfaces Learning vs Relations and/or
Concepts Adding or Removing
Remove Relations. When we have generated the
OOBN, concepts related by a semantic relations were
represented by instances of classes encapsulated in
each other, and we have expect that the learning pro-
cess will identify the variables that interact between
the two instances. If no common interface is identi-
fied, then these two concepts should be independent.
So their semantic relation have to be checked.
Figure 2: Enrichment process: an example of removing a
relation (S
R
is a semantic relation). Here we suppose that
after performing the learning process, we didn’t find nodes
from C
cp
1
that reference nodes from C
cp
2
. Thus, we can
propose to delete the semantic relation which appears in the
ontology.
Add Concepts/Relations. A class c
i
communicates
via its interface with a set S
c
of classes. If S
c
is a
singleton then we can simply propose to add a new
relation between concepts representing these classes
in the underlying ontology. Otherwise, we can use
KEOD 2011 - International Conference on Knowledge Engineering and Ontology Development
192
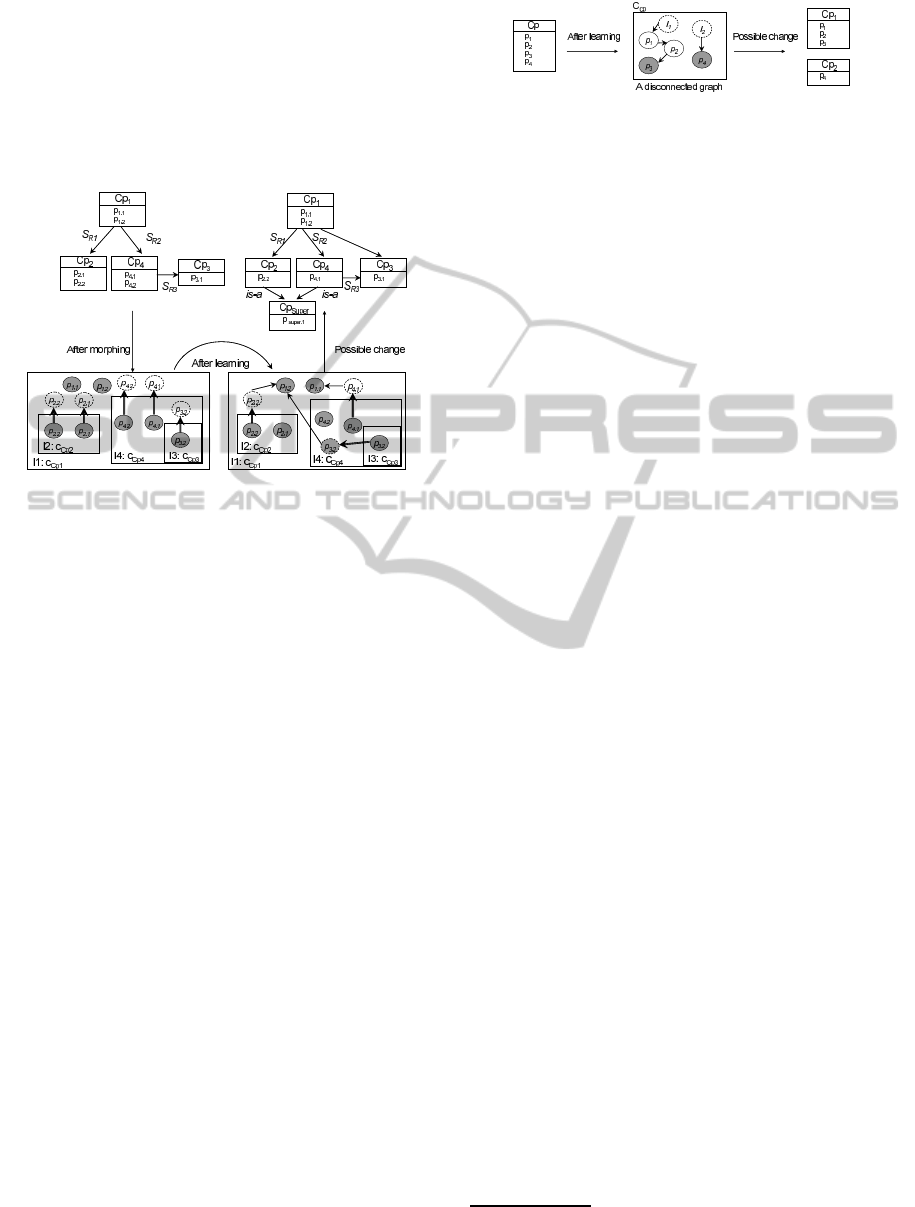
this exchange between classes whether by translating
it into relations or concepts allowing the factorization
of some other ones already present in the ontology. If
some classes in S
c
similar sets of nodes and have sim-
ilar structures, then we can extract a super-concept
over them. Otherwise, these relations may be trans-
lated into relations in the ontology.
Figure 3: Enrichment process: an example of adding con-
cepts and relations (S
R1
, S
R2
and S
R3
are semantic rela-
tions). Here we suppose that p
2.1
and p
4.2
have the same
state space and their respective classes C
cp
2
and C
cp
4
com-
municate with the same class C
cp
1
. Thus, in the ontological
side, we can define a super-concept over cp
2
and cp
4
having
p
super
as property which substitute both p
2.1
and p
4.2
. Note
thatC
cp
3
communicates also with C
cp
1
, but as it doesn’t rep-
resent shared properties with the other classes, then we will
simply add a new relation between cp
3
and cp
1
in the on-
tology.
4.3.2 Classes Learning vs Concepts Redefinition
As defined above, each class c in the OOBN is a DAG
overits three sets of nodesI
c
, H
c
and O
c
. Suppose that
the result of the learning process, was a disconnected
graph (as the example of figure 4), this means that
I
c
, H
c
and O
c
are divided into multiple independent
connected components (two in figure 4). Thus, nodes
of each component are not really correlated with those
of the other components. This can be translated in
the ontological side by proposing to deconstruct the
corresponding concept into more refined ones, where
each concept represents a component of the discon-
nected graph.
The possible changes are then communicated to
an expert via a warning system which detects the
changes and allows the expert to state actions to be
done. If he chooses to apply the change, he shall first
denominate the discovered relations and / or concepts.
Figure 4: Enrichment process: an example of concept re-
definition.
5 RELATED WORK
In recent years, a panoply of works have been pro-
posed in order to combine PGMs and ontologies so
that one can enrich the other.
One line of research aims to extend existing on-
tology languages, such as OWL
1
, to be able to
catch uncertainty in the knowledge domain. Pro-
posed methods (Ding and Peng, 2004), (Yang and
Calmet, 2005), (Costa and Laskey, 2006) use ad-
ditional markups to represent probabilistic informa-
tion attached to individual concepts and properties in
OWL ontologies. Other works define transition ac-
tions in order to generate a PGM given an ontology
with the intention of extending ontology querying to
handle uncertainty while keeping the ontology for-
malism intact (Bellandi and Turini, 2009).
On the other hand, some solutions proposed the
use of ontologies to help PGMs construction. Some of
them are designed for specific applications (Helsper
and van der Gaag, 2002), (Zheng et al., 2008), while
some others give various solutions to handle this is-
sue (Fenz et al., 2009), (Ben Messaoud et al., 2011).
However, all these solutions are limited to a re-
strained range of PGMs, usually BNs. So, they ne-
glect some ontology important aspects such as repre-
senting concepts having more than one property, non
taxonomic relations, etc. Moreover, the main idea
behind these methods was to enhance ontology rea-
soning abilities to support uncertainty. However, we
cannot provide a good basis for reasoning while we
do not have a well defined ontology, which takes into
consideration changes of its knowledge domain.
Thanks to the mapping process found between
ontologies and OOBNs, our 2OC approach allowed
us to deal with ontologies without significant restric-
tions. We focused on concepts, their properties, hier-
archical as well as semantic relations and we showed
how these elements would be useful to automatically
generate a prior OOBN structure, this latter is then
learned using observational data. This mixture of se-
mantical data provided by the ontology and observa-
tional data presents a potential solution to discover
1
ttp://www.w3.org/TR/2004/REC-owl-features-
20040210/
A TWO-WAY APPROACH FOR PROBABILISTIC GRAPHICAL MODELS STRUCTURE LEARNING AND
ONTOLOGY ENRICHMENT
193

new knowledge which is not yet expressed by the on-
tology thus, our idea was to translate new relations
discovered by the learning process into knowledge
which may be useful to enrich the initial ontology.
6 CONCLUSIONS AND FUTURE
WORKS
In this paper, we have proposed a new two-way ap-
proach, named OOBN-Ontology Cooperation (2OC)
for OOBN structure learning and automatic ontology
enrichment. The leading idea of our approach is to
capitalize on analyzing the elements that are common
to both tasks with the intension of improving their
state-of-the-art methods. In fact, our work is consid-
ered as an initiative aiming to set up new bridges be-
tween PGMs and ontologies. The originality of our
method lies first, on the use of the OOBN framework
which allowed us to address an extended range of on-
tologies, second, on its bidirectional benefit as it en-
sures a real cooperation, in both ways, between on-
tologies and OOBNs.
Nevertheless, this current version is subject to sev-
eral improvements. As a first line of research, we aim
to implement our method and test it on real world ap-
plications based on ontologies, furthermore, in this
work, our aim was to provide a warning system able
to propose a set of possible changes to the ontology
engineers. The discovered relations and / or con-
cepts have to be denominated so, as possible research
direction, we will be interested in natural language
processing (NLP) methods to allow the automation
of this process. Our last perspective concerns the
use of another PGM, Probabilistic Relational Models
(Getoor et al., 2007),whose characteristics are similar
to OOBNs.
REFERENCES
Bangsø, O., Langseth, H., and Nielsen, T. D. (2001). Struc-
tural learning in object oriented domains. In Proceed-
ings of the 14th International Florida Artificial Intel-
ligence Research Society Conference, pages 340–344.
Bangsø, O. and Wuillemin, P.-H. (2000). Object oriented
bayesian networks: a framework for top-down spec-
ification of large bayesian networks with repetitive
structures. Technical report, Aalborg University.
Bellandi, A. and Turini, F. (2009). Extending ontology
queries with bayesian network reasoning. In Proceed-
ings of the 13th International Conference on Intelli-
gent Engineering Systems, pages 165–170, Barbados.
Ben Ishak, M., Leray, P., and Ben Amor, N. (2011).
Ontology-based generation of object oriented
bayesian networks. In Proceedings of the 8th
Bayesian Modelling Applications Workshop, pages
12–20, Barcelona, Spain.
Ben Messaoud, M., Leray, P., and Ben Amor, N. (2011).
Semcado: a serendipitous strategy for learning causal
bayesian networks using ontologies. In Proceedings
of the 11th European Conference on Symbolic and
Quantitative Approaches to Reasoning with Uncer-
tainty, pages 182–193, Belfast, Northern Ireland.
Costa, P. and Laskey, K. (2006). PR-OWL: A framework
for probabilistic ontologies. Frontiers In Artificial In-
telligence and Applications, 150:237–249.
Ding, Z. and Peng, Y. (2004). A probabilistic extension to
ontology language OWL. In Proceedings of the 37th
Hawaii International Conference On System Sciences.
Fenz, S., Tjoa, M., and Hudec, M. (2009). Ontology-based
generation of bayesian networks. In Proceedings of
the 3rd International Conference on Complex, Intelli-
gent and Software Intensive Systems, pages 712–717,
Fukuoka, Japan.
Getoor, L., Friedman, N., Koller, D., Pfeffer, A., and Taskar,
B. (2007). Probabilistic relational models. In Getoor,
L. and Taskar, B., editors, An Introduction to Statisti-
cal Relational Learning, pages 129–174. MIT Press.
Gruber, T. (1993). A translation approach to portable ontol-
ogy specifications. Knowledge Acquisition, 5(2):199–
220.
Helsper, E. M. and van der Gaag, L. C. (2002). Building
bayesian networks through ontologies. In Proceedings
of the 15th European Conference on Artificial Intelli-
gence, pages 680–684, Amsterdam.
Khattak, A. M., Latif, K., Lee, S., and Lee, Y.-K. (2009).
Ontology evolution: A survey and future challenges.
In The 2nd International Conference on u-and e- Ser-
vice, Science and Technology, pages 285–300, Jeju.
Koller, D. and Pfeffer, A. (1997). Object-oriented bayesian
networks. In Proceedings of the 13th Conference on
Uncertainty in Artificial Intelligence, pages 302–313,
Providence, Rhode Island, USA. Morgan Kaufmann.
Langseth, H. and Nielsen, T. D. (2003). Fusion of domain
knowledge with data for structural learning in object
oriented domains. Journal of Machine Learning Re-
search, 4:339–368.
Pearl, J. (1988). Probabilistic reasoning in intelligent sys-
tems. Morgan Kaufmann, San Franciscos.
Stojanovic, L., Maedche, A., Stojanovic, N., and Motik, B.
(2002). User-driven ontology evolution management.
In Proceedings of the 13th International Conference
on Knowledge Engineering and Knowledge Manage-
ment, pages 285–300, Siguenza, Spain.
Yang, Y. and Calmet, J. (2005). Ontobayes: An ontology-
driven uncertainty model. In The International Con-
ference on Intelligent Agents, Web Technologies and
Internet Commerce, pages 457–463, Vienna, Austria.
Zheng, H., Kang, B.-Y., and Kim, H.-G. (2008). An
ontology-based bayesian network approach for rep-
resenting uncertainty in clinical practice guidelines.
In ISWC International Workshops, URSW 2005-2007,
Revised Selected and Invited Papers, pages 161–173.
KEOD 2011 - International Conference on Knowledge Engineering and Ontology Development
194
