A MEMETIC ALGORITHM FOR A CONTINUOUS CASE OF THE

BERTH ALLOCATION PROBLEM

Geraldo Regis Mauri

, Larice Nogueira de Andrade

and Luiz Antonio Nogueira Lorena

Federal University of Esp´ırito Santo - UFES, Alegre, ES, Brazil

Federal University of Triˆangulo Mineiro - UFTM, Uberaba, MG, Brazil

National Institute for Space Research - INPE, S˜ao Jos´e dos Campos, SP, Brazil

Keywords:

Berth allocation, Memetic algorithm, Simulated annealing, Combinatorial optimization.

Abstract:

This work presents a Memetic Algorithm heuristic to solve a continuous case of the Berth Allocation Problem

(BAP). The BAP deals with programming and allocating ships to berthing areas along a quay. In general, the

continuous case considers that ships have different lengths and can moor anywhere along the quay. However,

we consider a quay divided in berths that have limited areas and different equipments to handle the ships. So,

we must to assign the ships to berths and determine the berthing time and position for each ship. We treat

the ships as rectangles to be placed into a space × time area avoiding overlaps and satisfying time window

constraints. Our MA uses a Simulated Annealing (SA) as the local search mechanism, and SA is also applied

in a stand alone way to solve the BAP. A two-phase heuristic is also presented to compute the berthing time

and position for all of ships during MA and SA execution. Computational results are performed on a set of

instances proposed in the literature and new best-known solutions are presented.

1 INTRODUCTION

The port importance grows with the increasing

progress in the construction technology of great ships.

Besides, due to the improved trades among the na-

tions caused by globalization, the frequency of trans-

ports among ports also increases, mainly due to the

constant economical growth and volume of the trade

among several countries.

Maritime transport can be seen as a central pil-

lar for the international trade. Approximately 80% of

global market is conducted through the sea (Buhrkal

et al., 2011). Moreover, in 2008 the ﬂeet of ships car-

rying containers had an increase in capacity of 17.3

million tons, or 11.9%, and now represents 13.6% of

world total. In 2009, the world merchant ﬂeet reached

1.19 million, an increase of 6.7% compared to Jan-

uary 2008, and since the beginning of the decade, the

number of containers increased by 154% (UNCTAD,

2009).

Due to intense ﬂow of ships and containers in

ports, these are forced to invest heavily to accommo-

date the ships, deepening and widening channels and

building new installations of moor, everything to min-

imize the service time of the ships. So, a port should

operates in an efﬁcient way (Hansen et al., 2008).

The allocation and programming of ships to berths

have a primary impact on the efﬁciency of these op-

erations (Imai et al., 2003). Vis and Koster (2003)

present a discussion about the decision problems that

appear in a port. A classiﬁcation of the processes and

operations of different marine terminals is presented

by Steenken et al. (2004). The crucial problem in a

port administration is optimizing the balance among

the ships holder that demand fast services, and the

economical use of the available resources into the port

(Dragovic et al., 2005).

The Berth Allocation Problem (BAP) consists of

optimally assigning ships to berthing areas along a

quay in a port. The choice of “where” and “when”

the ships shall berth is the main decision to be made

in that process (Cordeau et al., 2005).

The BAP has a lot of physical and technical re-

strictions, among others. This makes possible to

model it in different ways. Considering the spatial

aspects of the berths, the BAP can be modeled as dis-

crete and continuous (Imai et al., 2005). In the dis-

crete case, the quay is divided into several berths and

only one ship is serviced at a time in every berth, re-

gardless of their length. In the continuous case, there

is no division of the quay and thus the ships can moor

at any position. Another conception for the continu-

105

Regis Mauri G., Nogueira de Andrade L. and Antonio Nogueira Lorena L..

A MEMETIC ALGORITHM FOR A CONTINUOUS CASE OF THE BERTH ALLOCATION PROBLEM.

DOI: 10.5220/0003636601050113

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 105-113

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

ous case considers that the quay is divided in berths,

but the big ships can occupy more than one posi-

tion, thus allowing small ships to share their berth

(Cordeau et al., 2005). This last approach represents

the real cases of a more appropriate way, where some

berths have different equipments (reaching limited ar-

eas) to operate speciﬁc type of cargo(container of var-

ious sizes, for example).

If we consider the arrival of ships, the BAP can be

still treated as static or dynamic (Imai et al., 2001).

The static case assumes all ships already in port for

the service, while the dynamic case allows ships to

arrive at any time (estimated in advance). In recent

works, we have notice that the term “dynamic” has

been unusual, because in practice, the static case is

not close to real situations. Then, the remainder of

this paper will denotes the “dynamic and continuous

case” only as continuous case.

This paper solves a continuous case of the BAP by

means of an effective Memetic Algorithm (MA) using

a Simulated Annealing (SA) as the local search mech-

anism. SA is also applied in a stand alone way, and

both SA and MA use a two-phase heuristic to com-

pute the berthing time and position for all of ships

presenting results that outperform those obtained by

another heuristic approach reported in the literature.

The remainder of this paper is organized as fol-

lows. The next section reports a brief literature re-

view. Section 3 presents details about the BAP. Our

MA, SA and two-phase heuristic are described in Sec-

tion 4. Computational results are presented in Section

5, followed by conclusions in Section 6.

2 BRIEF LITERATURE REVIEW

Initial works about the BAP appear at the end of the

80s, but these works have been gaining focus in the

last 10 years.

Approaches based on using heuristic alternatives

to solve the BAP are the most explored, and we be-

lieve that such methods have been predominating for

allowing the inclusion of several constraints in a “soft

way”.

Imai et al. (2001) present a method based on La-

grangian relaxation of the original problem. Two

years later, Imai et al. (2003) upgraded their approach

considering different service priorities between the

ships. Furthermore, the authors proposed a Genetic

Algorithm as a method of solution. The same authors

also treated a continuous case (see Imai et al. (2005)).

Cordeau et al. (2005) present a Tabu Search based

heuristic for solve two different models for a discrete

case of the BAP. They also present a TS heuristic for

a continuous case of the problem. They compared

their TS with a truncated branch-and-bound applied

to an exact formulation. Comparisons were made for

the discrete case. For the continuous approach, the

TS was able to solving more realistic instances than

those previously considered by other authors. The

proposed TS could handles various features of real-

life problems, including time windows and favorite

and acceptable berthing areas. The objective function

treated a weighted sum of the ship’s service times.

Mauri et al. (2008a) proposed an approach based

on the application of Simulated Annealing for solving

the discrete case of BAP. The authors treat the prob-

lem as a Multi-Depot Vehicle Routing Problem with

Time Windows (MDVRPTW). The computational re-

sults improved those obtained by CPLEX and Tabu

Search proposedby Cordeau et al. (2005). Mauri et al.

(2008b) solves the discrete case of the BAP by using a

hybrid method called PTA/LP, which uses the Popula-

tion Training Algorithm with a Linear Programming

model through a Column Generation technique. The

results improved those shown in their previous work.

Giallombardo et al. (2010) present two models

based on quadratic and linear programming to repre-

sent a discrete case of the BAP. Moreover, the authors

use a Tabu Search and a mathematical programming

technique to solve instances based on real data.

Recently, Buhrkal et al. (2011) reviewed some ap-

proaches about BAP and described three models for

the discrete berth allocation problem. The authors

proven the optimal solutions for some instances pre-

sented by Cordeau et al. (2005) for the discrete case

of BAP.

3 BERTH ALLOCATION

As mentioned before, the Berth Allocation Prob-

lem (BAP) consists of optimally assigning ships to

berthing areas along a quay in a port respecting sev-

eral physical and technical restrictions.

Related to the berth position, there exist con-

straints concerning to the depth of the water (allow-

able draft) and to the maximum distance from the

most favorable location along the quay, considering

the ship’s length and the location of the outbound and

inbound containers.

Some ports have hard allowable draft constraints

since they are located in geographical regions subject

to meaningful tide variation. In such cases, the ships

only can berth in known time windows of about two

hours around the high tide.

Besides this time window constraint, there exist

the time windows for completion time of ship servic-

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

106

ing (Cordeau et al., 2005). The handling time of a

ship depends on its berthing point and it is a function

of the distance from the berth to the pick-up and de-

livery area of containers stored in the port yard. This

dependency strongly affects the performance of the

port (Cordeau et al., 2005).

Managers want to minimize both port and user

costs, which are related to service time. The objec-

tive of the BAP is usually to minimize the total ser-

vice time of all ships. Since ships do not have equal

importance, a weighted sum of the ship service times

may better reﬂect the management practice of some

ports. The weights in this sum can represent a pric-

ing scheme (demurrage) over delayed operations, the

number of container moves, and the urgent need of a

given load. Penalty terms can be explicitly included

in the objective function, for example, the demurrage

cost when the service time of a ship exceeds the con-

tracted value (see Barros et al. (2011), for example).

As reported by Cordeau et al. (2005), the BAP

can be represented in a two-dimensional area (see

Figures 1 and 2) considering the ships as rectangles

whose dimensions are length, including a safety mar-

gin, and handling time (space x time area). So, the

BAP can be deﬁned by placing these rectangles in the

port area without overlapping and satisfying several

constraints.

The spatial dimension is ignored in the discrete

case of the BAP, and the berths can be described as

ﬁxed length segments, or simple points. For the con-

tinuous case, we consider that the quay is also divided

in berths (as explained in Section 1), but now the spa-

tial dimension is not ignored. We will denote these

approaches as BAP-D and BAP-C, respectively. For

the BAP-C, a ship may occupy part of neighboring

berths (see Cordeau et al. (2005)).

100

150

200

250

300

SPACE

TIME

B10

B11

B12

B13

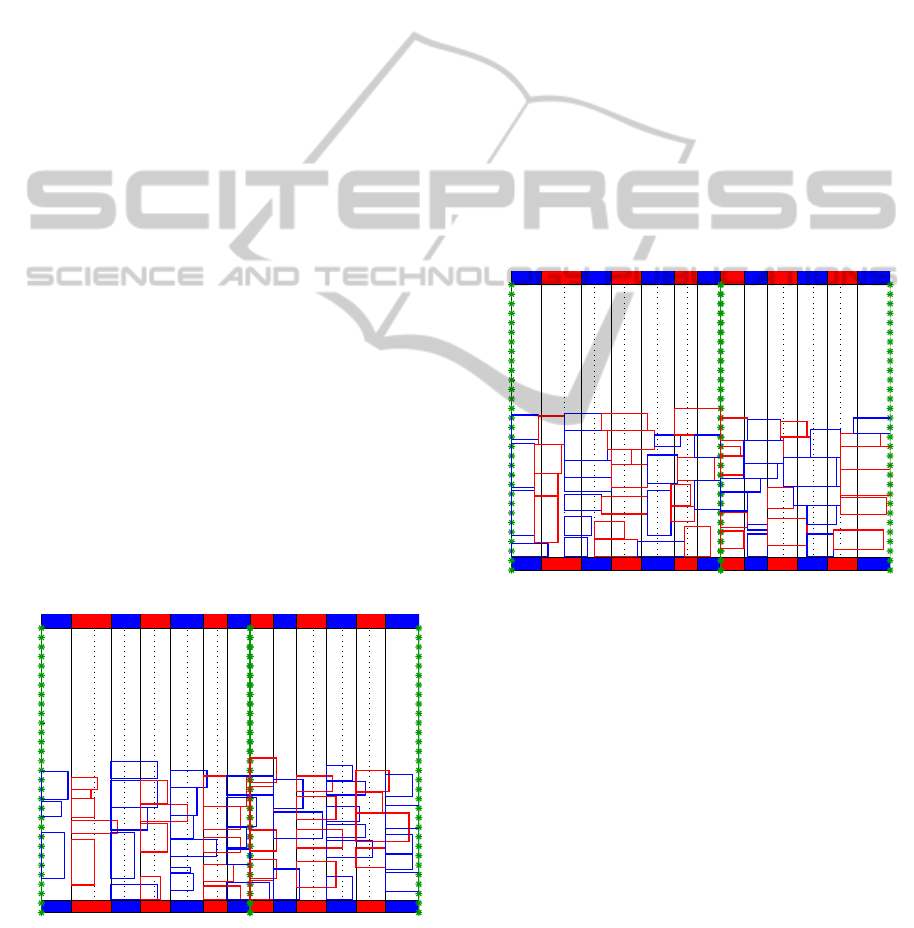
Figure 1: Optimal solution for BAP-D: i01 = 1409.

Cordeau et al. (2005) considered a quay divided

into berths with two parts, left and right. So, each

berth k has two neighbors, the right part of the berth

k−1 and the left part of the berth k+1. Discontinuous

segments must be also considered, representing the

initial and ﬁnal berths and also natural obstacles, as

sharp curves, for example. In these cases, the berths

have only one neighbor and they are not divided (see

berths 1, 7, 8, 9 and 13 in Figure 1).

Figure 1 presents an optimal solution (cost =

1409) for the instance i01 (one of those used on our

computational experiments - see Section 5) consider-

ing the BAP-D approach. In this ﬁgure, we used the

colors red and blue to enhance visualization. Then,

each rectangle represents a ship, and the blue ones are

assigned to the nearest blue berth. This is also true

for the red ones. Marked green lines indicate discon-

tinuities and solid and dotted black lines indicate the

different berths and their parts (left and right), respec-

tively. Bottom and top ﬁlled boxes indicate the start

and the end of availability time for the berths. We can

see that there are overlapping of ships, and the dis-

continuous berths are not respected.

100

150

200

250

300

SPACE

TIME

B10

B11

B12

B13

Figure 2: Best-known solution for BAP-C: i01 = 1613.

A best-known solution (cost = 1613 - found by

our MA described in Section 4) for this same instance

(i01) considering the continuous case (BAP-C) is pre-

sented in Figure 2. No overlapping and violations of

the discontinuities are observed in this case.

Cordeau et al. (2005) reported that BAP-D can be

regarded as a relaxation of the BAP-C, because a solu-

tion for the BAP-D can violate the spatial constraints

(compare Figures 1 and 2). So, we notice that a so-

lution for the BAP-D can be seen as a lower bound

for the BAP-C (Imai et al., 2005). In this paper, we

will treat only the continuous case (BAP-C) aiming to

minimize the sum of the times while the ships stayed

into the port (service times), i.e., the elapsed time

since the ships incoming, berthing and handling. Fig-

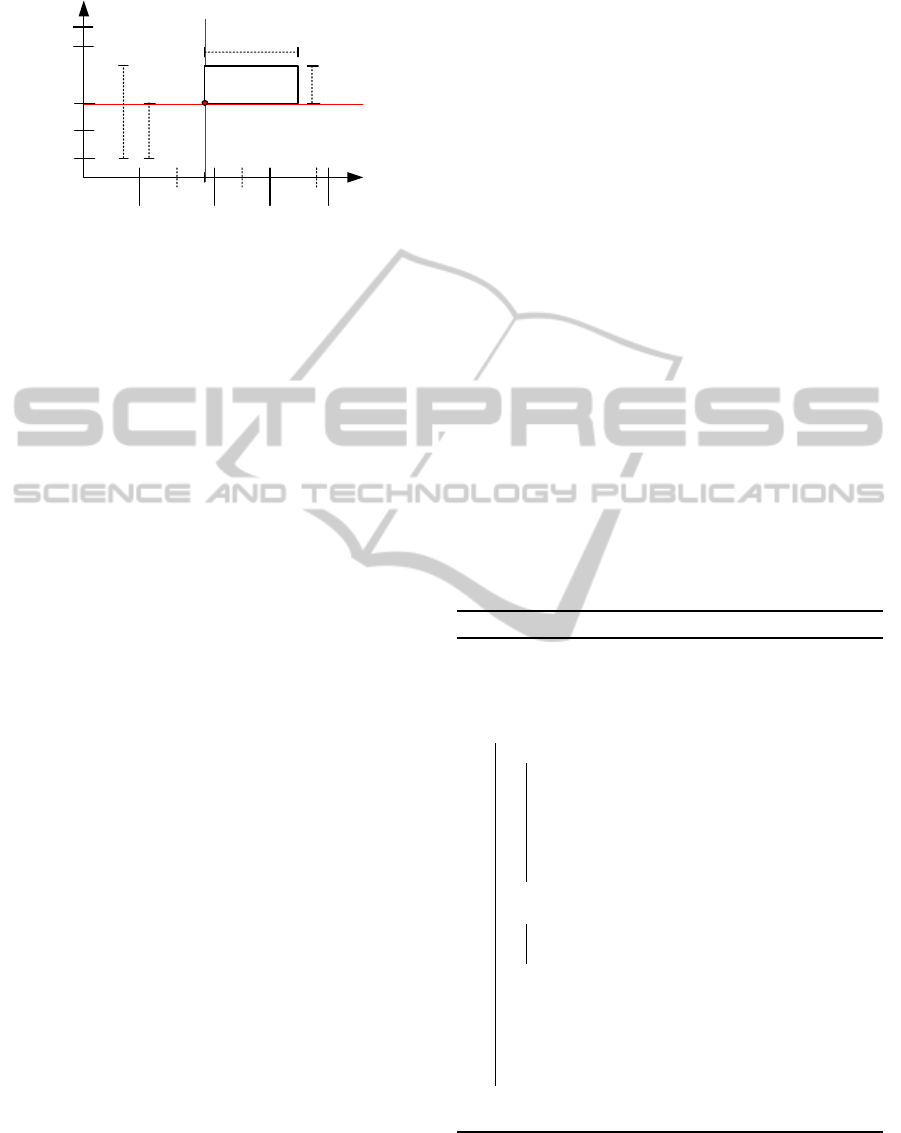
ure 3 illustrates the service time for a ship i assigned

to a hypothetical berth 3.

A MEMETIC ALGORITHM FOR A CONTINUOUS CASE OF THE BERTH ALLOCATION PROBLEM

107

berth 1 berth 2 berth 3

...

berth 4

waiting

time

service time

),(

TIME

SPACE

ship i

Figure 3: Data description for the ships berthing.

Now, our objective can be described as to assign

n ships to m berths. Then, we can determine, in ad-

vance, the following data:

• N: set of ships, n = |N|;

• M: set of berths, m = |M|;

• a

: arrival time of ship i;

• b

: limit time to complete the service for ship i;

• t

: handling time of ship i at berth k;

• z

: length of ship i (including a safety margin);

• s

: start of availability time for berth k;

• e

: end of availability time for berth k;

• P

: start position for berth k (including the right

part of its left neighbor);

• P

: ﬁnal position for berth k (including the left

part of its right neighbor);

• R

: neighbor at right side for berth k (0 if none);

• L

: neighbor at left side for berth k (0 if none).

Using these data, we must to assign the ships to

berths determining the berthing time and position for

each ship i (i = 1,.. . , n). We will denote them as T

and P

respectively. These variables can be seen as

the coordinates for the left lower corner point of the

rectangles (see Figure3).

Several mathematical models for both BAP-D and

BAP-C can be found in the literature. See for ex-

ample Imai et al. (2001), Nishimura et al. (2001),

Cordeau et al. (2005) and Buhrkal et al. (2011). How-

ever, we did not ﬁnd any model for the continuous

case (BAP-C) that considers all of the features previ-

ously described, as discontinuities, the use of neigh-

boring berths and different berths capacity (different

handling times). A comparison among some recent

models is presented by Buhrkal et al. (2011).

4 MEMETIC ALGORITHM

In this section, we present our MA algorithm for the

BAP-C.

Evolutionary algorithms have been applied suc-

cessfully for solve several classes of combinatorial

optimization problems. Memetic Algorithms (MAs)

are evolutionary algorithms which can be seen as

Genetic Algorithms (GAs) that uses a local search

procedure to improve the search reﬁning individuals

(Moscato, 1999).

The “meme” suggests a cultural evolution within

a lifetime, and MA uses this concept by applying a

local search to represent a learning to the individuals.

The MAs use evolutionary operators to ﬁnd

promising regions on the search space applying a lo-

cal search procedure to intensify the investigation in

these regions. According to Moscato and Norman

(1992), the basic idea of the MAs consists of explor-

ing the neighborhood of the solutions obtained by a

GA searching to local optimal.

The recombination mechanism (crossover) allows

that the mixing of information from one generation

can be transmitted to its offspring, and the mutation

introduces innovation in the population. More details

about the MAs are reported by Moscato (1999).

Algorithm 1: Memetic Algorithm - MA.

1 Input: #gen, #pop, #eli, #cro, #mut and #ls

2 curPop ← INITIAL-POPULATION(#pop)

3 bstInd ← the best individual in curPop

4 newPop ← {

5 for i = 1 to #gen do

6 for j = 1 to #cros do

7 p

← SELECT(one from the best #eli% in

curPop)

8 p

← SELECT(one from all in curPop)

9 of f ← CROSSOVER(p

)

10 of f ← LOCAL-SEARCH(of f,#ls)

11 newPop ← ADD(of f)

12 end

13 for j = 1 to #mut do

14 ind ← SELECT(one from newPop)

15 MUTATION(ind)

16 end

17 ind ← TAKE(the best individual in newPop)

18 bstInd ← BEST(bstInd,ind)

19 DISCARD(curPop)

20 curPop ← the best #pop individuals in newPop

21 newPop ← {

22 end

23 Output: bstInd

Our MA contains some user-controlled parame-

ters, and we will denote them as: #gen, #pop, #eli,

#cro, #mut and #ls. #gen is the number of generations

for the algorithm converging; #pop is the population

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

108

size (number of individuals); #eli is a percentage of

the best individuals in a population (elite); #cro and

#mut are the number of crossover and mutation per-

formed at each generation; and #ls is the “deep” of

the local search.

First, #pop individuals (solutions) are randomly

created to form an initial population. #cros crossovers

are performed between two parents randomly selected

from the current population: one elite individual and

any other. A local search is performed over the re-

sulting offspring, and it is added into a new popu-

lation. Then, #mut mutations are applied over indi-

viduals randomly selected from the new population.

The best individual in the new population is stored,

the current population is discarded and the new pop-

ulation becomes the current one. This process is re-

peated for #gen generations. Our MA pseudo-code is

presented in Algorithm 1.

We now describe the main elements of our MA

implementation for the BAP-C.

Individual Representation. An individual represents

one possible solution for the BAP-C and it is de-

scribed as a matrix with the lines indicating the berths

and the columns presenting the sequence of ships to

be handling at each berth. Figure 4 illustrates an in-

dividual (solution) for a hypothetical problem with 4

berths and 14 ships.

8 12

13Berth 1

Berth 4

Berth 3

Berth 2

Figure 4: Individual representation.

Initial Population. A random individual can be con-

structed through a simple and balanced heuristic. Ini-

tially, the ships are organized by incoming order on

port (a

) and distributed to the berths in a random

way. In this process, the selected berth must always

be able to assist the selected ship. This procedure en-

sures that each ship will be assigned to a berth that

must be able to attend it, i.e., the berth length is suf-

ﬁcient to receive the ship and the berth’s equipments

are suitable to operate the type of cargo into the ship.

So, this procedure is repeated for #pop times forming

an initial population. This procedure does not guaran-

tee that the berthing time (T

) and position (P

) for the

ship i (i = 1, . . . , n) present no overlappingon time and

space dimensions. This strategy is based on the dis-

tribution heuristic presented by Mauri et al. (2008a,b)

and the FCFS-G heuristic presented by Cordeau et al.

(2005).

Computing Berthing Times and Positions. After

generating a random individual (solution), we must

deﬁne the berthing time and position for all of ships.

We present a two-phase heuristic to determine these

values.

• Phase 1: Berthing time and position for all of

ships assigned to a speciﬁc berth are set to initial

values according to Algorithm 2. At this moment,

the berthing times are set to equal the arrival times

of the ships, if the berth is available. The berthing

positions are set to equal the start position of the

berth. This phase is applied to give initial values

for P

and T

, that are updated in phase 2. This pro-

cedure is based on the ones presented by Mauri

et al. (2008a,b), Pacheco et al. (2010) and Ribeiro

et al. (2011) adding the position deﬁning.

Algorithm 2: Two-phase heuristic - phase 1.

1 Input: berth k

2 for each ship i assigned to k do

3 T

←

(

max





i = 1

max



i−1



i > 1

4 P

← P

5 end

• Phase 2: The spatial distribution for the ships to

the berths are updated and improved. This proce-

dure updates the berthing times and positions con-

sidering a simple idea: if some overlap is detected

for each ship, its berthing time is delayed until

eliminate all of them. If a berth has no neighbor

at the left side, all of ships assigned to it have the

berthing position set to equal the start position of

the berth, i.e., all of ships (rectangles) are aligned

at left. If a berth has no neighbor at the right side,

all of ships assigned to it have the berthing po-

sition set to equal the ﬁnal position of the berth

minus the ship length, i.e., all of ships are aligned

at right. Finally, if a berth has neighbors on both

sides, we try to ﬁt the ships among the ones as-

signed to the two neighbor berths. This procedure

is described in Algorithm 3.

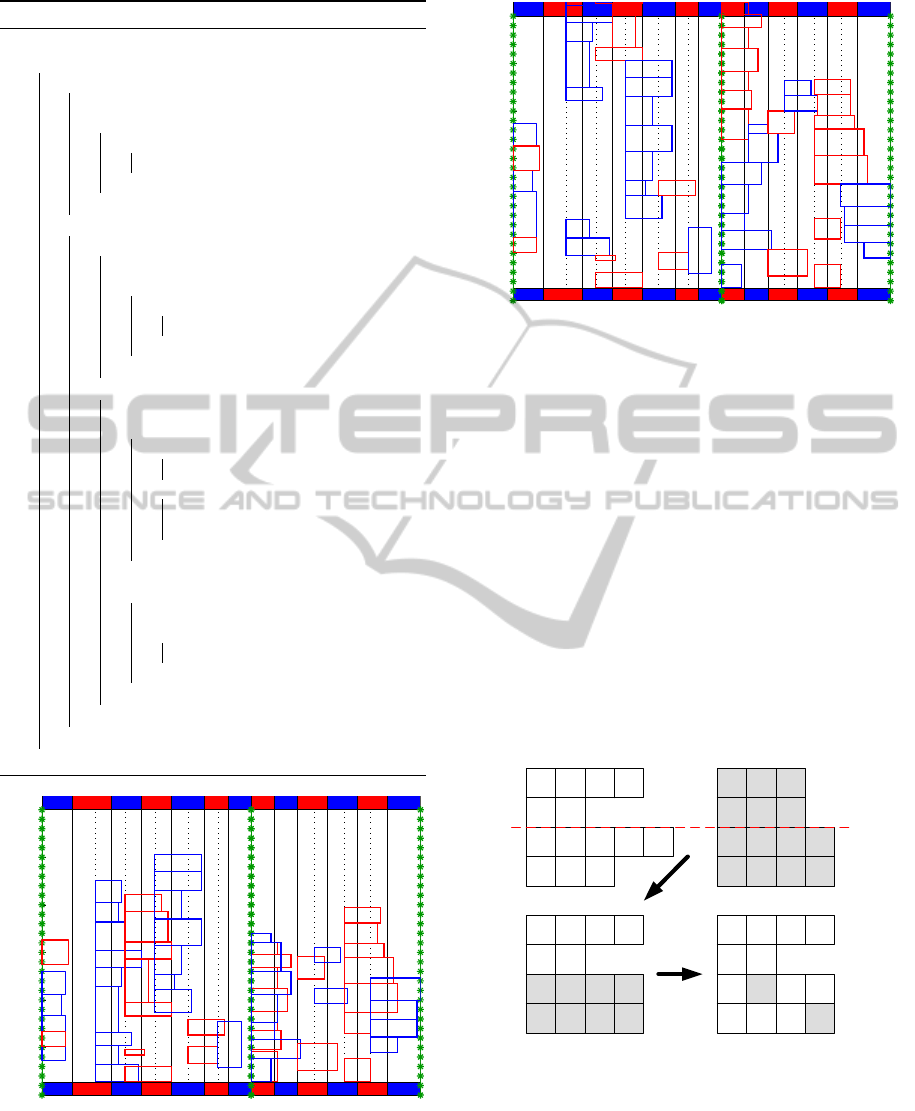
Figures 5 and 6 illustrate a randomly generated in-

dividual after running only phase 1 and after phases 1

and 2 of our two-phase heuristic.

In the ﬁrst case (Figure 5), only the phase 1 of our

heuristic was performed, and we can note that over-

lapping were not treated. In the second case (Figure

6), both phases were computed and no overlapping is

presented. However, we can observe that some ships

violate the deadlines for some berths (see berths 2, 3,

4, 8 and 9), and these violations must be eliminated by

our MA through a penalized objective function (see

expression 1).

A MEMETIC ALGORITHM FOR A CONTINUOUS CASE OF THE BERTH ALLOCATION PROBLEM

109

Algorithm 3: Two-phase heuristic - phase 2.

1 Input: berth k

2 for each ship i assigned to k do

3 if L

= 0 then

4 P

← P

5 for each ship j assigned to k+ 1 do

6 if i overlaps j then

7 T

← max(T

k+1

)

8 end

9 end

10 else

11 if R

= 0 then

12 P

← P

− z

13 for each ship j assigned to k− 1 do

14 if i overlaps j then

15 T

← max(T

k−1

)

16 end

17 end

18 else

19 P

← P

20 while ∃ j assigned to k− 1 overlapping i do

21 if (P

+ z

≥ P

) and (P

+ z

≤ P

) then

22 P

← P

+ z

23 else

24 T

← max(T

k−1

)

25 P

← P

− z

26 end

27 end

28 while ∃ j assigned to k+ 1 overlapping i do

29 T

← max(T

k+1

)

30 while ∃ l assigned to k− 1 overlapping i do

31 T

← max(T

k−1

)

32 end

33 end

34 end

35 end

36 end

100

150

200

250

300

SPACE

TIME

B10

B11

B12

B13

Figure 5: Random solution after phase 1.

Individual Evaluation. We may notice that our two-

phase heuristic guarantees that no overlapping will

occur and no ship will exceed the spatial limit of the

berths. However, our solutions can still present viola-

100

150

200

250

300

SPACE

TIME

B10

B11

B12

B13

Figure 6: Random solution after phases 1 and 2.

tions on the limit time to complete the service of the

ships (b

,∀i = 1,... , n) and on the end of availability

time of the berths (e

,∀k = 1,...,m). So, we deﬁne a

function to compute the cost of an individual consid-

ering a weight λ to penalty theses violations (see ex-

pression 1). This function is composed by three terms

representing the service times for the ships (sum of

the times when the ships stayed in port) and the sum

of violating deadlines for the ships and berths respec-

tively. The ﬁtness measure used to evaluate the indi-

viduals was 1/ f(I).

f(I) =











∑

k∈M

∑

i∈N



+ t

− a



∑

k∈M

∑

i∈N

max



0,T

+ t

− b



∑

k∈M

∑

i∈N

max



0,T

+ t

− e



(1)

8 12

13 2

13 4

off

Figure 7: Crossover.

Crossover. A one-point based crossover was im-

plemented. Given two parents p

and p

, a number

of berths x (0 < x < m) is randomly selected and

then the ﬁrst x berths from p

are inserted into the

offspring of f. Then, the last m − x berths from p

are inserted into of f removing the duplicated ships,

and the ships that have not been assigned to any berth

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

110

are randomly allocated at the last m− x berths in of f.

The ships assigned to each of the last m − x berths

are organized by incoming order on port (a

) and the

two-phase heuristic is applied only to these berths in

of f. Finally, function 1 is used to compute the cost

(f(of f)) and ﬁtness for of f (1/ f(o f f )). Figure 7

illustrates our crossover.

Mutation. Three different procedures explored in

previous works (see Mauri et al. (2008a), Pacheco

et al. (2010) and Ribeiro et al. (2011)) were used

to compose a neighborhood structure: Re-order

ships, Re-allocate ship and Swap ships. We will

denote them as ω

, ω

and ω

respectively. ω

obtained by randomly choosing two ships of the

same berth, and swapping them; ω

is obtained by

inserting a ship i chosen at random from some berth

into another berth in a position chosen at random;

and ω

is obtained by swapping two ships from two

different berths, all chosen at random. So, a mutation

is deﬁned by applying one of these procedures

(randomly selected) over an individual followed

by performing the two-phase heuristic on the modi-

ﬁed berths. Finally, the individual’s ﬁtness is updated.

Local Search. A traditional Simulated Annealing

(SA) presented in previous works (see Ribeiro et al.

(2011)) was used as the local search mechanism for

our Memetic Algorithm (MA). The neighborhood

structure for our SA were composed by selecting (at

random) one of the three procedures adopted in the

Mutation. We must emphasize that low values for the

SA parameters were used into our MA to make only a

fast local search. These parameters values were: α =

0.95, T

start

= 10, T

frozen

= 0.01 and SA

max

= #ls (de-

ﬁned in the next section).

5 COMPUTATIONAL RESULTS

This section presents a comparative evaluation of our

Memetic Algorithm (MA) and Simulated Annealing

(SA) applied in a stand alone way. Both heuristics

were applied 10 times to each instance, and to be fair,

we imposed a time limit as unique stopping criterion

for them: 120 seconds for each instance, i.e., the same

time used by Tabu Search (TS) proposed by Cordeau

et al. (2005).

The SA and MA heuristics have stopping condi-

tions based on the temperature and on the number of

generations, respectively. If they reach their stopping

conditions before the time limit, we restart the heuris-

tic from the best solution identiﬁed during the search.

This process is repeated until the heuristic reaches the

time limit.

The SA and MA heuristics were coded in C++

and ran on a PC with Intel Core i3 processor of 2.66

GHz with 4 GB of RAM Memory under Windows

7 operating system. Cordeau et al. (2005) had use a

Sun workstation (900 MHz) to run their TS. Our algo-

rithms were tested on a BAP instances set randomly

generated by Cordeau et al. (2005). This set is com-

posed by 30 different instances with 60 ships and 13

berths, and it was provided to us by the authors in a

previous situation.

The parameters of SA and MA were chosen em-

pirically after running them over three randomly se-

lected instances. We ran SA and MA ﬁve times for

each parameter setting, and the setting yielding the

best average results was chosen. So, the ﬁnal values

for the SA parameters were: T

start

= 15000, T

frozen

0.01, α = 0.975, SA

max

= 1000. The parameters for

our MA were: #pop = 30, #eli = 10, #cro = 25, #mut

= 5 and #ls = 7. The parameters used by SA (as a

local search) inside the MA were deﬁned in Section

A special attention was given to the weight λ, be-

cause we note that a large value for this weight often

traps the search in a locally suboptimal solution. So,

the weight value was set to 10 (λ = 10).

Table 1: Results from our SA and MA heuristics.

SA MA

Instance f(I

∗

) Time (s) f(I

∗

) Time (s)

bst avge bks bst bst avge bks bst

i01 1639 1661.60 21.45 58.45 1613 1666.50 37.49 85.41

i02

1326 1341.20 28.17 41.47 1326 1347.80 51.91 75.85

i03

1242 1254.90 28.12 58.51 1234 1261.90 20.58 79.99

i04

1392 1416.40 31.79 65.63 1392 1421.00 36.36 84.54

i05

1285 1300.80 16.53 91.54 1285 1302.00 8.55 90.02

i06

1461 1492.00 17.28 67.69 1461 1492.10 5.84 85.67

i07

1333 1347.10 19.48 64.68 1333 1352.00 12.38 92.50

i08

1425 1470.30 34.69 80.23 1425 1466.40 12.88 91.94

i09

1651 1693.80 55.22 59.20 1651 1698.20 40.06 89.57

i10

1371 1380.40 40.67 61.45 1371 1393.00 38.93 72.64

i11

1574 1606.50 20.82 59.57 1557 1602.10 5.70 72.93

i12

1541 1568.60 22.21 56.87 1537 1565.80 7.64 88.01

i13

1457 1468.60 18.39 47.73 1449 1482.50 23.66 83.02

i14

1284 1289.80 16.98 58.90 1287 1306.90 6.57 80.19

i15

1362 1376.50 19.10 65.92 1362 1394.20 14.44 75.85

i16

1508 1539.00 14.49 70.45 1508 1581.10 4.28 87.78

i17

1310 1321.40 52.24 54.70 1318 1335.30 68.71 83.41

i18

1529 1549.10 25.59 59.68 1519 1552.10 21.68 89.47

i19

1572 1614.60 33.32 62.10 1573 1628.60 26.00 84.78

i20

1438 1456.40 52.98 50.21 1428 1469.30 67.47 91.01

i21

1478 1494.80 16.03 86.28 1481 1510.40 7.64 80.47

i22

1484 1519.00 22.22 78.94 1484 1521.00 12.57 86.19

i23

1425 1456.00 23.58 54.52 1425 1456.10 3.56 84.86

i24

1365 1375.30 15.99 73.48 1359 1383.40 14.40 87.65

i25

1546 1578.20 45.12 53.87 1546 1604.50 38.04 79.12

i26

1475 1507.40 30.07 62.51 1475 1520.10 22.25 80.51

i27

1356 1371.50 15.39 88.81 1356 1382.30 6.59 70.23

i28

1504 1525.20 44.35 69.11 1486 1553.90 53.80 81.15

i29

1340 1351.20 16.03 55.84 1338 1360.80 6.76 74.49

i30

1512 1547.30 15.17 82.53 1512 1555.60 7.43 84.63

Avge 1439.50 1462.50 27.11 64.70 1436.37 1472.23 22.81 83.13

Table 1 presents a detailed comparison between

our SA and MA performance. Five different columns

are used for all results: the instance name, the best so-

A MEMETIC ALGORITHM FOR A CONTINUOUS CASE OF THE BERTH ALLOCATION PROBLEM

111

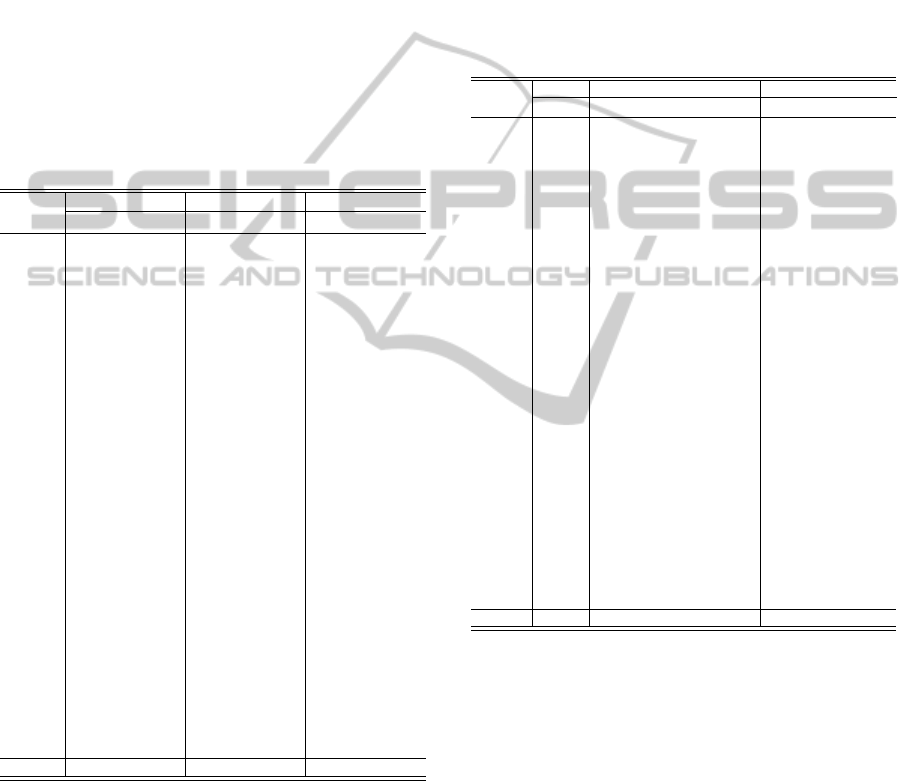
lution found (f(I

∗

) → bst), the averagesolution found

(avge), the computational time (bks) to reach the best-

known so far (TS by Cordeau et al. (2005)) and the

computational time to found the best solution for each

algorithm (Times(s) → bst).

In Table 1, we can note that MA found ten best

solutions and four worse than SA. The others sixteen

solutions were equal. Despite the differences, we no-

tice that MA is slightly better, but in general, the so-

lutions of SA and MA are very close. This fact can

indicate that our solutions are probably next to the

optimal ones. We conﬁrmed this situation in Tabel

3. The average values (last line) are also close, and

we emphasize that our heuristics ﬁnd the same solu-

tions of TS proposed by Cordeau et al. (2005) using

less than 30 seconds.

Table 2: Comparison with the TS of Cordeau et al. (2005).

TS SA MA

Instance

bst dev (%) bst dev (%) bst dev (%)

i01 1706 5.77 1639 1.61 1613 0

i02 1355 2.19 1326 0 1326 0

i03

1286 4.21 1242 0.65 1234 0

i04 1440 3.45 1392 0 1392 0

i05

1352 5.21 1285 0 1285 0

i06

1565 7.12 1461 0 1461 0

i07 1389 4.20 1333 0 1333 0

i08

1519 6.60 1425 0 1425 0

i09 1713 3.76 1651 0 1651 0

i10

1411 2.92 1371 0 1371 0

i11 1696 8.93 1574 1.09 1557 0

i12

1629 5.99 1541 0.26 1537 0

i13 1519 4.83 1457 0.55 1449 0

i14

1369 6.62 1284 0 1287 0.23

i15

1455 6.83 1362 0 1362 0

i16 1715 13.73 1508 0 1508 0

i17

1322 0.92 1310 0 1318 0.61

i18 1594 4.94 1529 0.66 1519 0

i19

1673 6.42 1572 0 1573 0.06

i20 1450 1.54 1438 0.70 1428 0

i21

1565 5.89 1478 0 1481 0.20

i22 1618 9.03 1484 0 1484 0

i23

1539 8.00 1425 0 1425 0

i24

1425 4.86 1365 0.44 1359 0

i25 1590 2.85 1546 0 1546 0

i26

1567 6.24 1475 0 1475 0

i27 1458 7.52 1356 0 1356 0

i28

1550 4.31 1504 1.21 1486 0

i29 1415 5.75 1340 0.15 1338 0

i30

1621 7.21 1512 0 1512 0

Avge 1516.87 5.59 1439.50 0.24 1436.37 0.04

Table 2 presents a comparison among our algo-

rithms and the Tabu Search by Cordeau et al. (2005).

The columns present the best solutions found (bst)

by each heuristic and their deviations (dev(%)). The

deviations are calculated as dev(%) = 100 × (bst −

bst

∗

)/bst

∗

, where bst

∗

is the best-known solution

value obtained by any of the three heuristics for a

given instance. We can observe that both SA and MA

found better solutions than TS for all of instances, and

MA presents better solutions than SA.

Table 3 shows the gaps over the lower bounds

(BAP-D) presented by Buhrkal et al. (2011). The

column OPT BAP-D reports the optimal solutions

(proven by Buhrkal et al. (2011)) for the discrete case

of BAP. As mentioned before, according to Cordeau

et al. (2005) and Imai et al. (2005), solutions for

the BAP-D are lower bounds for the BAP-C. The

gaps shown in the last columns are calculated as

Gaps(%) = 100× (X −Y)/Y, where X is the best so-

lution found by each of three heuristics for the BAP-C

and Y is the value for the lower bound (OPT BAP-D).

Table 3: Comparison with the optimal solutions for BAP-D.

OPT BAP-C Gaps (%)

Instance

BAP-D TS SA MA BT SA MA

i01 1409 1706 1639 1613 21.08 16.32 14.48

i02

1261 1355 1326 1326 7.45 5.15 5.15

i03

1129 1286 1242 1234 13.91 10.01 9.30

i04 1302 1440 1392 1392 10.60 6.91 6.91

i05

1207 1352 1285 1285 12.01 6.46 6.46

i06 1261 1565 1461 1461 24.11 15.86 15.86

i07

1279 1389 1333 1333 8.60 4.22 4.22

i08 1299 1519 1425 1425 16.94 9.70 9.70

i09

1444 1713 1651 1651 18.63 14.34 14.34

i10 1213 1411 1371 1371 16.32 13.03 13.03

i11

1368 1696 1574 1557 23.98 15.06 13.82

i12 1325 1629 1541 1537 22.94 16.30 16.00

i13

1360 1519 1457 1449 11.69 7.13 6.54

i14

1233 1369 1284 1287 11.03 4.14 4.38

i15 1295 1455 1362 1362 12.36 5.17 5.17

i16

1364 1715 1508 1508 25.73 10.56 10.56

i17 1283 1322 1310 1318 3.04 2.10 2.73

i18

1345 1594 1529 1519 18.51 13.68 12.94

i19 1367 1673 1572 1573 22.38 15.00 15.07

i20

1328 1450 1438 1428 9.19 8.28 7.53

i21 1341 1565 1478 1481 16.70 10.22 10.44

i22

1326 1618 1484 1484 22.02 11.92 11.92

i23 1266 1539 1425 1425 21.56 12.56 12.56

i24

1260 1425 1365 1359 13.10 8.33 7.86

i25

1376 1590 1546 1546 15.55 12.35 12.35

i26 1318 1567 1475 1475 18.89 11.91 11.91

i27

1261 1458 1356 1356 15.62 7.53 7.53

i28 1359 1550 1504 1486 14.05 10.67 9.35

i29

1280 1415 1340 1338 10.55 4.69 4.53

i30 1344 1621 1512 1512 20.61 12.50 12.50

Avge 1306.77 1516.87 1439.50 1436.36 16.0 10.1 9.8

Looking at Table 3, it is interesting to highlight

the gaps over the optimal solutions for the BAP-D.

We can verify that our MA solutions are relatively

close to the optimal, because the average gap was of

9.8%. We may also note a signiﬁcant reduction over

the solutions provided by the Tabu Search proposed

by Cordeau et al. (2005).

6 CONCLUSIONS

In this paper we have developed a Memetic Algorithm

(MA) to solve a continuous case of the Berth Alloca-

tion Problem (BAP).

MA was employed by using a Simulated Anneal-

ing (SA) as the local search mechanism and a two-

phase heuristic to compute the berthing time and po-

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

112

sition for all of ships. SA was also applied in a stand

alone way.

On test instances, both SA and MA yield good re-

sults and outperform the rather good Tabu Search of

Cordeau et al. (2005). Our results show a relative su-

periority of the MA, but SA also found good solu-

tions.

The integrated use of MA, SA and the two-phase

heuristic results in a powerful approach to solve the

continuous case of the BAP, providing good solutions

in low computational times.

MA showed to be extremely efﬁcient, presenting

small gaps over the best-known lower bounds and

suggesting that our solutions are probably close to op-

timal.

So, considering that the continuous case of the

BAP represents real situations in a more appropriate

way, and considering that BAP has a signiﬁcant im-

pact on the efﬁciency of the marine terminals, a mini-

mal reduction on the service times may reﬂects a gain

and/or economy of millions of dollars.

ACKNOWLEDGEMENTS

The authors acknowledge Esp´ırito Santo Research

Foundation - FAPES (process 45391998/09) and

National Council for Scientiﬁc and Technological

Development - CNPq (processes 300747/2010-1,

300692/2009-9 and 470813/2010-5) for their ﬁnan-

cial support.

REFERENCES

Barros, V. H., Costa, T. S., Oliveira, A. C. M., and Lorena,

L. A. N. (2011). Model and heuristic for berth allocation

in tidal bulk ports with stock level constraints. Comput-

ers & Industrial Engineering, 60:606–613.

Buhrkal, K., Zuglian, S., Ropke, S., Larsen, J., and Lusby,

R. (2011). Models for the discrete berth allocation

problem: a computational comparison. Transportation

Research Part E: Logistics and Transportation Review,

47:461–473.

Cordeau, J. F., Laporte, G., Legato, P., and Moccia, L.

(2005). Models and tabu search heuristics for the berth

allocation problem. Transportation Science, 39:526–

538.

Dragovic, B., Park, N. K., and Radmilovic, Z. (2005). Sim-

ulation modelling of ship-berth link with priority service.

Maritime Economics & Logistics, 7:316–335.

Giallombardo, G., Moccia, L., Salani, M., and Vacca, I.

(2010). Modeling and solving the tactical berth alloca-

tion problem. Transportation Research Part B, 44:232–

245.

Hansen, P., Oguz, C., and Mladenovic, N. (2008). Variable

neighborhood search for minimum cost berth allocation.

European Journal of Operational Research, 191:636–

649.

Imai, A., Nishimura, E., and Papadimitriou, S. (2001).

The dynamic berth allocation problem for a container

port. Transportation Research Part B: Methodological,

35:401–417.

Imai, A., Nishimura, E., and Papadimitriou, S. (2003).

Berth allocation with service priority. Transportation Re-

search Part B: Methodological, 37:437–457.

Imai, A., Sun, X., Nishimura, E., and Papadimitriou, S.

(2005). Berth allocation in a container port: using a

continuous location space approach. Transportation Re-

search Part B, 39:199–221.

Mauri, G. R., Oliveira, A. C. M., and Lorena, L. A. N.

(2008a). Heur´ıstica baseada no simulated annealing apli-

cada ao problema de alocac¸˜ao de berc¸os. GEPROS -

Gest˜ao da Produc¸˜ao, Operac¸˜oes e Sistemas, 1:113–127.

Mauri, G. R., Oliveira, A. C. M., and Lorena, L. A. N.

(2008b). A hybrid column generation approach for the

berth allocation problem. Lecture Notes in Computer Sci-

ence, 4972:110–122.

Moscato, P. (1999). Memetic algorithms: a short introduc-

tion. In Corne, D., Dorigo, M., Glover, F., Dasgupta, D.,

Moscato, P., Poli, R., and Price, K. V., editors, New ideas

in optimization. 219–234.

Moscato, P. and Norman, M. (1992). A memetic approach

for the travelling salesman problem: implementation of

a computational ecology for combinatorial optimization

on message-passing systems. In Proceedings of the Inter-

national Conference on Parallel Computing and Trans-

portation Applications. 177–186.

Nishimura, E., Imai, A., and Papadimitriou, S. (2001).

Berth allocation planning in the public berth system by

genetic algorithms. European Journal of Operational

Research, 131:282–292.

Pacheco, A. V. F., Ribeiro, G. M., and Mauri, G. R. (2010).

A grasp withpath-relinking for the workover rig schedul-

ing problem. International Journal of Natural Comput-

ing Research, 1:1–14.

Ribeiro, G. M., Mauri, G. R., and Lorena, L. A. N. (2011).

A simple and robust simulated annealing algorithm for

scheduling workover rigs on onshore oil ﬁelds. Comput-

ers & Industrial Engineering, 60:519–526.

Steenken, D., Voss, S., and Stahlbock, R. (2004). Container

terminal operation and operations research: a classiﬁca-

tion and literature review. OR Spectrum, 26:3–49.

UNCTAD (2009). Review of maritime transport. United

Nations conference on trade and development.

Vis, I. F. A. and Koster, R. D. (2003). Transshipment of

containers at a container terminal: an overview. Euro-

pean Journal of Operational Research, 147:1–16.

A MEMETIC ALGORITHM FOR A CONTINUOUS CASE OF THE BERTH ALLOCATION PROBLEM

113