AN INNOVATIVE PROTOCOL FOR COMPARING PROTEIN

BINDING SITES VIA ATOMIC GRID MAPS

M. Bicego

1,2

, A. D. Favia

, P. Bisignano

, A. Cavalli

and V. Murino

1,2

PLUS Lab, Istituto Italiano di Tecnologia, I-16163 Genoa, Italy

Dipartimento di Informatica, University of Verona, I-37134 Verona, Italy

Department of Drug Discovery and Development (D3), Istituto Italiano di Tecnologia, I-16163 Genoa, Italy

Keywords:

Protein similarity, 3D points alignment, Iterative closest point, Drug design, Multitarget.

Abstract:

This paper deals with a novel computational approach that aims to measure the similarities of protein binding

sites through comparison of atomic grid maps. The assessment of structural similarity between proteins is a

longstanding goal in biology and in structure-based drug design. Instead of focusing on standard structural

alignment techniques, mostly based on superposition of common structural elements, the proposed approach

starts from a physicochemical description of the proteins’ binding site. We call these atomic grid maps. These

maps are preprocessed to reduce the dimensionality of the data while retaining the relevant information. Then,

we devise an alignment-based similarity measure, based on a rigid registration algorithm (the Iterative Closest

Point –ICP). The proposed approach, tested on a real dataset involving 22 proteins, has shown encouraging

results in comparison with standard procedures.

1 INTRODUCTION

In this paper, we address a fundamental issue in

structural biology and in structure-based drug design,

namely the characterization, for comparative pur-

poses, of a set of macromolecular entities such as pro-

teins (Kahraman and Thornton, 2008). Since struc-

ture is more conserved than sequence, the most com-

mon approaches rely on the superposition of common

structural elements. Such methods allow researchers

to compare, with an increasing degree of difﬁculty,

a) different conformations of the same protein, b)

homologous proteins and, c) evolutionarily-unrelated

proteins.

Traditionally, structural alignment techniques rely

on the punctual superposition of correspondent atoms,

usually the protein backbones or C-α, in different

entries (Shindyalov and Bourne, 1998; Holm and

Sander, 1993). A more sophisticated class of pro-

tocols considers elements of the protein secondary

structures (Jung and Lee, 2000; Chen and Crippen,

2005; Kawabata, 2003). However, these reductionist

approaches, based on geometric hashing, do not take

into account the physicochemical complexity of the

systems. This is because they completely ignore the

ﬁelds produced by the macromolecule (e.g. the ones

experienced by interacting molecules) (Favia, 2011).

Furthermore, these methods cannot be safely applied

to evolutionarily-distant proteins, due to the lack of

sound correspondences between atoms.

To overcome these limits, we herein introduce a

new protocol, based on van der Waals potential en-

ergies (IUPAC, 1997) calculated at regularly spaced

points within a predeﬁned volume. The deﬁnition of

the volume is case-speciﬁc and is usually deﬁned ac-

cording to the binding site deﬁnition. This method

allows one a) to compare binding sites and, in a more

advanced application, b) to guide a more physico-

chemically sound structure alignment. Van der Waals

interactions between nonbonded atoms can be ex-

pressed as a function of their internuclear separation

through the Lennard-Jones equations. At each of the

regularly spaced points, a virtual atom type is placed

and its potential is evaluated. This atom type can be

thought of as a chemical probe that experiences the

protein ﬁelds. The energy at each grid point is deter-

mined by the set of parameters supplied for that par-

ticular probe, and is estimated as the summation over

all atoms of the macromolecule, within a non-bonded

cutoff radius, of all pairwise interactions. Different

probes experience different ﬁelds, according to their

assigned chemical features. Taken together, a mini-

mal set of selected probes, namely carbon, oxygen,

and hydrogen atoms, can give a useful description of

the studied volume based on shape (C probe), H-bond

donor, and acceptor propensity (H and O probes, re-

spectively) (see Fig. 1). Once this physicochemi-

cal description of the volume is achieved, it can be

413

Bicego M., D. Favia A., Bisignano P., Cavalli A. and Murino V..

AN INNOVATIVE PROTOCOL FOR COMPARING PROTEIN BINDING SITES VIA ATOMIC GRID MAPS.

DOI: 10.5220/0003637404050414

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 405-414

ISBN: 978-989-8425-79-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Grid point generation. An enclosing box is deﬁned within a protein active site (A). The grid maps can then be

conveniently visualize as isocontour maps. The carbon, oxygen and hydrogen maps are shown in (B), (C) and (D) at 0, -1 and

-0.6 kcal/mol isocontour level, respectively. The protein structure is shown in the background of the 4 panels.

used to compare a) different conformations of the

same protein and b) different proteins altogether. The

presented protocol is similar in spirit to the recently

developed protocol for ligand-binding site superposi-

tion and comparison based on Atomic Property Fields

(Totrov, 2011).

This paper introduces a computational approach

able to compare two or more proteins starting from

the above-mentioned physicochemical description of

their binding site. We call these descriptions atomic

grid maps. In particular, the idea is to exploit tech-

niques from the Computer Vision and Pattern Recog-

nition ﬁelds to devise similarity between maps in or-

der to understand and highlight relations between dif-

ferent proteins.

The computation of the similarity is carried out

in two steps: ﬁrst, a chemically plausible prepro-

cessing transforms the real-valued potential maps into

discrete-valued maps (which we call ”meta-maps”);

then, the meta-maps are compared using a rigid align-

ment algorithm (the Iterative Closest Point – ICP

((Besl and McKay, 1992; Chen and Medioni, 1992)),

setting the distance between the pair of proteins as the

alignment error. This alignment may be performed

either by using a single value of the meta-map or by

combining together all the values. A similarity clearly

expresses the relation between two proteins: a more

general view may be obtained by taking a set of pro-

teins, computing all the pairwise distances, and visu-

alizing all the relations through a hierarchical cluster-

ing approach (Jain and Dubes, 1988).

The proposed approach has been applied to a real

dataset composed of diverse X-ray structures of GSK-

3β, a protein involved in Alzheimer’s disease (Her-

nandez et al., 2009), as extracted from the Worldwide

Protein Data Bank (wwPDB) (Berman et al., 2003).

The similarity measures obtained with the proposed

approach have been compared with those obtained

through a time-consuming computational procedure

based on the comparison of structure-assisted virtual

screening ranked distributions (Bottegoni et al., 2011)

(which can be considered as the ”true” distances). We

will show in our experiments that the proposed com-

putational method can approximate these true dis-

tances in an encouraging way.

We note that this could be an invaluable drug

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

414

design tool. This is because representative confor-

mations of a studied protein could be used to run

time-demanding molecular simulations (e.g. dock-

ing), rather than using the whole ensemble of avail-

able structures. More broadly, when applied to un-

related proteins, the methodology could conveniently

highlight common hotspots that could be exploited

to design multitarget drugs (i.e. molecules capable

of binding different proteins). These are particu-

larly useful in treating complex diseases (Morphy and

Rankovic, 2006).

The remainder of the paper is organized as fol-

lows: Section 2 describes how potentials maps are

extracted. In Section 3, we present the proposed ap-

proach. Section 4 describes an experimental evalua-

tion that validates the methodology. Finally, in Sec-

tion 5, conclusions are drawn and future perspectives

are envisaged.

2 POTENTIAL MAPS

The active sites of the selected structures of GSK-3β

were ﬁrst superimposed using the McLachlan algo-

rithm (McLachlan, 1982) as implemented in the pro-

gram ProFit

. Then, van der Waals forces were com-

puted, using the AutoGrid software as distributed with

AutoDock4.2 (Morris et al., 2009). AutoGrid solves

the Lennard-Jones equations at regularly spaced grid

points (0.375

A) enclosed in a box centered on the

center of mass of the atoms belonging to the active

site, spanning 14.25, 11.25 and 21

A along the three

axes. To give an accurate description of the site, three

diverse atom probes were placed at each node of the

grid to sense the protein environment, namely the car-

bon, hydrogen and oxygen probes. In particular, the

carbon probe accounts for the shape and hydropho-

bic features of the binding site, while the hydrogen

and the oxygen probes account for the hydrogen bond

propensity. Pairwise atomic interactions are approxi-

mated through the following equation:

V (r) =

−

= C

−n

− C

−m

(1)

Here, m and n are integers, C

and C

are constants

whose values vary according to the type of atoms and

probes involved and r is the distance between them.

At distances shorter than the equilibrium distance (in

correspondence to the minimum of the function), the

potential energy function increases rapidly (i.e. the

probe clashes with the protein), while at long dis-

tances the function tends to zero (i.e. the probe does

not feel the presence of the protein).

A.C.R. Martin http://www.bioinf.org.uk/software/proﬁt/

3 THE PROPOSED APPROACH

The goal of the proposed approach is to characterize

a set of proteins, each one described by a set of poten-

tials maps. The idea is to highlight the relations be-

tween the different proteins of the chosen set by de-

vising a similarity measure, which could potentially

be used in a clustering scenario to highlight all the

possible relations. Some different distances are de-

ﬁned and described in Sect. 3.2. These are all based

on a chemically sound preprocessing algorithm used

to simplify the potential maps, as described in the next

Section.

3.1 Preprocessing of Data: The

Meta-maps

AutoGrid produces real-valued potential maps. As

such, they are difﬁcult to interpret. Hence, we parsed

the three Auto-Grid readouts to yield a single map that

retains all the relevant information. A few considera-

tions must be made here:

• the oxygen and hydrogen probes are mutually ex-

clusive;

• both are considered to be more relevant, from a

chemical perspective, than the carbon probe;

• we were only interested in negative values (i.e.

when probes and protein do not clash)

• after a heuristically deﬁned cutoff, small differ-

ences in potential energies are negligible.

Bearing this in mind, every position of the potential

maps may be described with one of four different val-

ues:

• value ’1’: if the oxygen probe, in this posi-

tion, recorded a potential energy lower than -1

kcal/mol;

• value ’-1’: if the hydrogen probe, in this position,

recorded a value lower than -0.6 kcal/mol;

• value ’0’: if the carbon probe, in this position,

recorded any negative value of the potential en-

ergy function;

• no value if none of the above criteria were fulﬁlled

in this position;

In doing so, a net compression of the data is possi-

ble, yet the relevant information is retained and con-

veniently encoded into a single, ternary grid map.

3.2 Devising the Similarity

Once the meta-maps have been obtained, the next step

is to deﬁne the similarity measure. One reasonable

AN INNOVATIVE PROTOCOL FOR COMPARING PROTEIN BINDING SITES VIA ATOMIC GRID MAPS

415

strategy is to link the similarity to the alignment of

the meta-maps, in order to measure, in some sense,

how dissimilar two maps remain after maximizing the

overlap between them (it may also be seen as the op-

posite of the overlap ratio between two maps).

In particular, we investigated two different ap-

proaches:

1. Alignment based on a Single Value. Here, we

selected only those meta-maps points with a spe-

ciﬁc value (-1, 0 or 1). In this way, the alignment

was transformed into a simpler problem of regis-

tration of point clouds – where the term ”registra-

tion” describes the geometric alignment of a pair

of 3D data-point sets. This is a well-known prob-

lem in computer vision (Trucco and Verri, 1998),

and many techniques to solve it have been pro-

posed in the past. One of the most famous is the

Iterative Closest Point (ICP – (Besl and McKay,

1992; Chen and Medioni, 1992)), brieﬂy summa-

rized later in this section;

2. Alignment based on all Values. The distance

was computed by simultaneously using all the val-

ues of the metamaps.

Before entering into the details, we will review

the Iterative Closest Point (ICP) algorithm (Besl and

McKay, 1992; Chen and Medioni, 1992).

3.2.1 Iterative Closest Point Algorithm

Let us suppose that we have two sets of 3D points,

and V

. The registration consists of ﬁnding a 3D

transformation which, when applied to V

, minimizes

the distance between the two point sets. In general,

point correspondences are unknown. For each point

from the set V

, there exists at least one point on

the surface of V

that is closer to y

than all the other

points in V

. This is the closest point, x

. The basic

idea behind the ICP algorithm is that, under certain

conditions, closest points are a reasonable approxi-

mation to the true point correspondences. The ICP

algorithm can be summarized as follows:

1. For each point in V

, compute the closest point in

;

2. With the correspondence from step 1, compute the

incremental transformation (R

i, j

, t

i, j

);

3. Apply the incremental transformation from step 2

to the set V

;

4. If the change in total mean square error is less than

a threshold, terminate. Otherwise, go to step 1.

Besl and McKay (Besl and McKay, 1992) proved

that this algorithm is guaranteed to converge mono-

tonically to a local minimum of the mean square error.

Thus, a good initialization is required. To overcome

this problem, we manually pre-aligned the proteins

in our experiments. For step 2, efﬁcient, noniterative

solutions to this problem (known as the point set reg-

istration problem) were compared in (Lorusso et al.,

1997). The solution based on singular value decom-

position was found to be the best in terms of accuracy

and stability.

After the convergence of the algorithm, the total

mean square error represents the registration error be-

tween the two sets of points.

After the convergence of the algorithm, the total

mean square error represents the registration error be-

tween the two sets of points.

3.2.2 Single Value Analysis

Given two proteins to be compared, the distance is

computed via the following steps:

1. for every protein, the three potential maps are

preprocessed to produce the corresponding meta-

map;

2. from the meta-map, only points with a speciﬁc

value are extracted (for example, all points with

’0’ value). This results in a cloud of 3D points;

3. the two 3D point clouds (relative to the two pro-

teins) are registered through the ICP algorithm.

The registration error represents the ﬁnal distance.

3.2.3 Multiple Values Analysis

The previous approach is of course limited by the fact

that the meta-maps are decomposed in three different

non-overlapping sets, which are used alone – in this

sense using only partial information. It seems reason-

able, therefore, to try to develop a method that can

integrate and use all the information present in the

meta-maps. From a very general Pattern Recognition

point of view, this problem may be contextualized

in the Multiclassiﬁer theory (also called Multimodal

or Fusion theory, depending on the context). These

theories aim to integrate the potentially complemen-

tary information provided by different methodolo-

gies/representations in a particular problem, by ex-

ploiting the different peculiarities of the fused tech-

niques. This theory, ﬁrst introduced in the classiﬁ-

cation context (Ho et al., 1994; Kittler et al., 1998;

Melnik et al., 2004) and, more recently, in the clus-

tering context ((Topchy et al., 2005; Fred and Jain,

2005) and references therein), seems to be particu-

larly suited for the context we are investigating. In

particular, the information fusion could be performed

at three different levels (Ross and Jain, 2004): data or

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

416

feature level, where feature representations are com-

bined; score level, where scores derived from differ-

ent modalities (e.g. similarities) are composed to get

a new score; and decision level, where the ﬁnal out-

puts (i.e. clusterings or trees) of multiple strategies

are consolidated.

In this preliminary analysis, we investigate a very

simple yet promising approach, aimed at perform-

ing an integration at the distance level. The idea is

to derive three different single-value-based registra-

tions, leading to three different distance measures,

which are ﬁnally integrated in a ﬁnal distance mea-

sure. In more detail, given a protein pair (i, j), the

starting point is represented by the three distances

−1

(i, j), d

(i, j) and d

(i, j). The main goal is to

combine them in order to obtain a more meaningful

one. Clearly, in the multiclassiﬁer taxonomy provided

above, we are performing score-level fusion. In gen-

eral, fusion at score level is preferred (Duin and Tax,

2000; Tax et al., 2000). This is because it is rela-

tively easy to access and combine scores produced by

the different modalities. Furthermore, some studies

have reported its superiority against feature-level fu-

sion and decision-level fusion – e.g. (Kumar et al.,

2003). Many techniques have been proposed in the

past, with different characteristics. Here we use two

rules:

1. Mean Rule. In this case the three distances are

simply averaged.

(i, j) =

−1

(i, j) + d

(i, j)

(2)

Despite its simplicity, this rule (also called SUM

rule) has proven to be very competitive in many

applications, while maintaining many interesting

theoretical properties (Kittler et al., 1998).

2. Weighted Mean Rule. In this case, the new dis-

tance is a convex combination of the three dis-

tances:

W M

(i, j) = α

−1

(i, j) + α

(i, j)

(3)

such that

−1

+ α

= 1

Deﬁning the three weights may be difﬁcult. An

interesting theoretical analysis of linear combin-

ers for multiple classiﬁers systems can be found

in (Fumera and Roli, 2005). Here, we performed

a large scale analysis, trying many different val-

ues, and selecting a posteriori the best triplet. We

are aware that this a posteriori choice is not opti-

mal, and we are currently experimenting with an

alternative and cleverer search strategy, which is

based on problem-driven information (following

the rationale applied in the phylogeny context by

(Bicego et al., 2007)).

4 EXPERIMENTAL RESULTS

The proposed approach was validated using a protein

dataset comprising 22 proteins. In particular, the dif-

ferent distances were computed following the proce-

dure described in the previous section. In the speciﬁc

case of comparing protein structures, one procedure

to determine a reliable distance between them can

be achieved through an undeniably time-consuming

computational procedure (see below for details). The

main goal of this experimental evaluation was to com-

pare, within the speciﬁc set of proteins, these ”true

similarities” (similarities obtained via docking) with

the similarity obtained by our approach. We car-

ried out both a qualitative and a quantitative analy-

sis. For the qualitative analyses, we used the pro-

posed distances to derive a dendrogram – via a stan-

dard agglomerative hierarchical clustering approach

(Jain and Dubes, 1988). We made some observations

by comparing the trees obtained with our distances

and those obtained with the true ones. For the quan-

titative analyses, the proposed similarities were com-

pared with the true ones using the Mantel test (Man-

tel, 1967).

4.1 The Dataset

The protein dataset was composed of 22 X-ray pro-

tein structures of GSK-3β as available at the wwPDB.

Being obtained under different experimental condi-

tions, the structures were available at different crys-

tallographic resolutions and were solved either alone

or in complex with structurally diverse inhibitors (see

Tab. 1). As a direct consequence of this, the se-

lected PDB entries were conformationally distinct

from each other and each represented an experimen-

tally observed moment of the protein dynamics (see

Fig. 2).

GSK-3β is a pharmacological target for

Alzheimer’s disease and, due to the abundance

of experimentally determined data, structure-assisted

methods, such as molecular docking, are widely used

in drug discovery pipelines, both in academia and in

industry.

Before starting a virtual ligand screening, when a

number of X-ray structures of the same protein are

available, one fundamental question that should be

addressed is: how diverse are the included structures?

Having access to this information would allow re-

searchers to select only a minimal subset of entries,

which preserves most of the relevant variance, for

running time-demanding docking simulations. Un-

fortunately, it is still not possible to assess, a priori,

redundancy between entries for virtual screening pur-

AN INNOVATIVE PROTOCOL FOR COMPARING PROTEIN BINDING SITES VIA ATOMIC GRID MAPS

417

Table 1: Detailed list of the structures included in the dataset used in this study.

PDB

Entry

(Ref)

Resolution

(Å)

Chain

Residues

nhibitor

GNG

2.60

385

B: 28- 384

H8F

2.80

B: 35- 384

2.70

384

issing

120

126, 286

300)

B: 37-382 (missing 286-290)

1J1B

1.80

388

B: 23-386

(ANP)

phosphoaminophosphonic acid

adenilate

ester

1J1C

2.10

388

B:23-386

(ADP) adenosine- 5’-diphosphate

1PYX 2.40

386

(missing 120

124, 287

290)

B:35-386 (missing 120-124, 285-290, 384-

386)

(ANP) phosphoaminophosphonic acid-adenilate

ester

1Q3D 2.20

385

(missing

120

124,287

292

)

B:35-385 (missing 120-123,287-

292,384,385)

(STU) staurosporine

1Q3W 2.30

A:35

385

(missing 121

124,288

291

)

B:35-385 (missing 121-123, 287-291,384-

385)

(ATU) Alsterpaullone

1Q41 2.10

386

(missing

120

125,285

291

)

B:35-386 (missing 120-125,384-386)

(IXM) Indirubin-3’-monoxime

1Q4L 2.77

386

(missing

121

123,286

292

)

B:35-386 (missing 292-299,384-386)

(679) I-5

1Q5K 1.94

384

(missing 120,121,287

289

)

B:35-386 (missing 287-289,295-297)

(TMU)

A014418

1R0E 2.25 A/B:35-383 (missing 120-124)

(

DFN

)

{[(2S)

2,3

dihydroxypropyl]amino}phenyl)-4-(5-fluoro-1-

methyl-1H-indol-3-yl)-1H-pyrrole-2,5-dione

1UV

2.80

383

(BRW)

bromoindirubin

3’

oxime

2JLD 2.35

385

(missing 120,290)

B:35-384 (missing 292)

(AG1)

ruthenium pyridocarbazole

2O5K 3.20 A:35-384 (HBM) 7-hydroxy-1H-benzoimidazole

2OW3

2.80

A:35

386

(missing

119

122, 386)

B:35-386

(BIM) Bis(indoyl)maleimide–para-pyridinophane

3DU8 2.20

A:35

382

(missing 120

125,287

292)

B: 35-385 (missing 120-125,287-292)

(553)(7S)-2-(2-aminopyrimidin-4-yl)-7-(2-

fluoroethyl)-1,5,6,7-tetrahydropyrrolo[3,2-

c]pyridin-4-one

3F7Z 2.40

A:35

383

(missing 122

124,288

294)

B:35-383 (missing 120-125,290-293)

(34O

)

(1,3

benzodioxol

yl)

[(3

fluoro

methoxy-phenyl)methylsulfanyl]-1,3,4-oxadiazole

3F88 2.60

A/B:35-383 (missing 120-125,288,289)

(2HT) 3-methylbenzonitrile

(3HT) 5-[3-(4-methoxyphenyl)benzimidazol-5-yl]-

3H-1,3,4-oxadiazole-2-thione

3I4B

2.30

A:33-385

B:36-382

(Z48)

[(1S)

hydroxy

phenylethyl]

methyl- 2-(phenylamino)pyrimidin-4-yl]-1H-

pyrrole- 2-carboxamide

3GB2 2.40 A:35-119;125-286; 290-383

(G3B) 2

methyl

[(S)

methylsulfinyl]phenyl}

1-benzofuran-5-yl)-1,3,4-oxadiazole

3L1S 2.90

A:25

118 (missing 32,33,34);

126-285;300-384

B:36-422 (missing 120-121; 286-300;383-

420)

(Z92) (4E)-4-[(4-chlorophenyl)hydrazono]-5-(3,4-

dimethoxyphenyl)-2,4-dihydro-3H-pyrazol-3-one

poses.

To this end, the set used in this study was ﬁrst

characterized using a standard molecular docking

simulation, described below. This procedure is com-

putationally demanding, and may be unfeasible in real

life scenarios for larger datasets of protein structures.

Nevertheless, it allowed us to generate a ground truth,

to be used retrospectively to assess the accuracy of the

proposed method.

4.1.1 The Ground Truth

In a molecular docking simulation, a molecule is com-

putationally docked at a protein active site with the

aim of predicting possible modes of interaction be-

tween the two. A number of poses are generated

and ranked according to the associated estimation

of the binding energy (score). Top scoring poses

are usually the ones considered, since these are sup-

posedly the ones that occur experimentally. In a

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

418

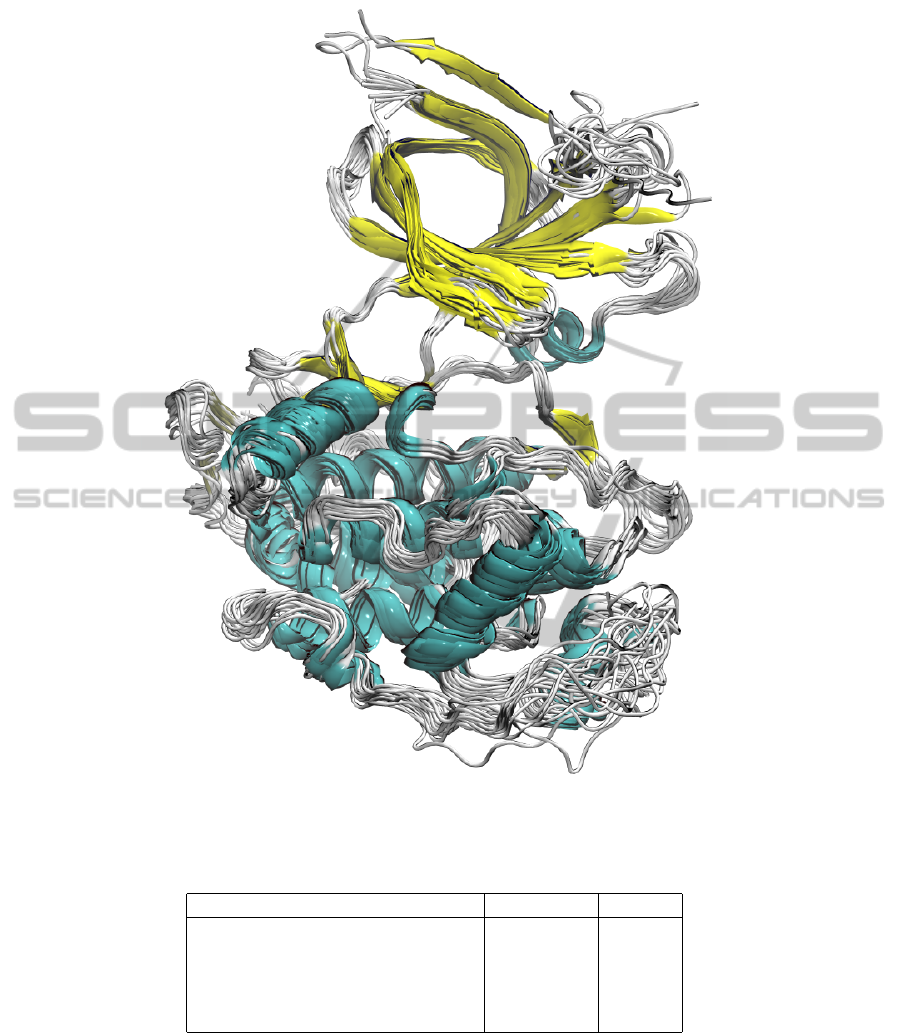
Figure 2: Structural superposition of the 22 PDB entries employed in this study. The structures are depicted in ribbon and

coloured according to the secondary structure elements.

Table 2: Correlations computed with the Mantel test for the different approaches.

Method Correlation p-value

Single value (-1) 0.708 0.001

Single value (0) 0.240 0.071

Single value (+1) 0.305 0.020

Multi values - mean rule 0.548 0.001

Multi values - weighted mean rule 0.721 0.001

virtual screening effort, a number of molecules are

docked at an enzyme-binding site and their bind-

ing afﬁnities are estimated. Assuming that, for each

molecule, only one pose is taken into account (i.e.

the top scoring one), the ﬁnal ranked distribution

will reﬂect the molecular preferences of a given pro-

tein. In fact, different proteins will reward differ-

ent classes of molecules, characterized by speciﬁc

physico-chemical features. An extension of this con-

sideration is that different conformations of the same

protein will reward different molecules too. This is

because docking algorithms treat these conformations

as if they were different molecular entities altogether.

In this context, the ranked distribution indirectly de-

scribes the physicochemical characteristics of a pro-

tein. We can think of these as ﬁngerprints, where each

AN INNOVATIVE PROTOCOL FOR COMPARING PROTEIN BINDING SITES VIA ATOMIC GRID MAPS

419

0.1

1I09

1GNG

1H8F

2O5K

1J1B

1J1C

1Q3D

1Q4L

1PYX

3DU8

3F7Z

3F88

1Q3W

3GB2

2JLD

3L1S

1Q5K

1UV5

1Q41

3I4B

1R0E

2OW3

(a)

0.1

1GNG

1I09

2O5K

1H8F

1Q3W

3F88

3DU8

1PYX

1J1B

1J1C

3L1S

1UV5

1Q41

1Q5K

3I4B

1Q4L

2JLD

3GB2

1Q3D

2OW3

1R0E

3F7Z

(b)

Figure 3: Trees obtained with UPGMA of the phylip package: (a) ground truth; (b) obtained with ’-1’ map.

position in the rank represents a bit and the unique

molecule in that position represents its assigned value.

To obtain meaningful results, a reasonable number

of molecules should be used. The set should be big

enough to allow a ﬁne distinction between proteins,

yet small enough to be computationally feasible. It

should be composed of chemically diverse entries in

order to eliminate noise-generating redundancy. In

this procedure, a set of 6354 diverse compounds was

docked at each of the 22 protein structures. Pear-

sons correlation coefﬁcients calculated between the

obtained ranks represent the ﬁnal distance, on which

the clustering procedure can be built.

In a real life scenario, where millions of com-

pounds and several tens of proteins can be involved,

using ranked distributions for clustering purposes

could be unfeasible. Grid-driven clustering offers a

quicker approach to this challenge. Moreover, maps-

driven analysis can be more easily interpreted from a

chemical standpoint.

4.2 Quantitative Evaluation

Table 2 reports the correlation coefﬁcients between

the proposed methods and the ground truth distances

(we note that the correlation, in this case, takes val-

ues from -1 to +1 – the higher the value, the better the

result). In addition to the correlation factor, a p-value

is also provided, which measures the probability that

the same correlation is obtained if randomly permut-

ing the rows or the columns of one of the matrices.

Some observations may be drawn from the table:

• the information carried out by the three single-

value maps is rather different: the analysis based

on the single values 0 and +1 is not as good as the

analysis made with the value -1 – even if it shows

a positive correlation with the ground truth

• this is conﬁrmed by the results obtained with the

mean rule (which gives the same weight to all the

maps); a proper weighing of the three distances

yields better results.

• combining the three distances improves the

single-value analysis, thus conﬁrming the com-

plementary information present in the original

sources.

4.3 Qualitative Evaluation

Given the distance, a qualitative analysis could be car-

ried out by looking at trees obtained via the applica-

tion of clustering techniques to the similarity matrices

– the proposed ones and the ground truth ones. In par-

ticular, dendrograms were obtained with the UPGMA

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

420

clustering algorithm (as implemented in the Phylip

Package

). In Fig. 3 two trees are reported, namely

the ground truth one and the one obtained with the -1

map.

Rather than looking at the global similarity be-

tween trees, a perceptive comparison should focus

mostly on the local matches. This is because, above a

deﬁned cutoff, distances between entries tend to be

less consistent. Indeed, the map-driven tree repro-

duced nicely some of the trends recorded by the dock-

ing ranks. For instance, entries 1GNG, 1I09, 2O5K

and 1H8F were singletons, according to the ground

truth. As illustrated in Fig. 3, the oxygen map-

driven tree put 5 entries distant from the rest. Four

of those entries were indeed the ground truth single-

tons, while the remaining entry (i.e. 1QW3) was er-

roneously recognized as close to 1H8F. From a bio-

logical perspective, 3 out of those 4 entries were pe-

culiar cases, being the only proteins of the set whose

crystals lacked a molecule bound. Another very inter-

esting achievement is the pairing of 1J1B and 1J1C.

Those Xray structures in fact showed very similar

molecules bound, which in turn yielded highly com-

parable conformational rearrangements. Another no-

table result was found for the cluster composed of

entries 3L1S, 1UV5, 1Q41, 1Q5K and 314B, which

perfectly matched the one found in the ground truth.

Entries 3F88, 3DU8 and 1PYX clustered together in

the map-driven tree. The same trend was found in the

ground truth, with the exception of entry 3F7Z, which

was missing in the former. Overall, the remarkable

resemblance between the ground truth and the map-

driven trees speaks to the accuracy of the proposed

methodology in ﬁnding hidden relevant chemical pat-

terns in protein structures. Nonetheless, there is room

for improvement. For instance, in a less reductionist

approach, more atom probes could be used.

5 CONCLUSIONS

In this paper, we proposed a novel computational ap-

proach to comparing two or more proteins, starting

from a physico-chemical description of their binding

site (atomic grid maps). These maps were prepro-

cessed via a chemically plausible procedure that sim-

pliﬁed the data while retaining the relevant informa-

tion. Different alignment-based similarity measures

were proposed based on a rigid registration algorithm.

The proposed approach was tested on a real dataset in-

volving 22 proteins. Retrospective evaluations, both

All information on software and models could be found

at http://evolution.gs.washington.edu/phylip.html.

qualitative and quantitative, proved the feasibility of

the method.

ACKNOWLEDGEMENTS

We kindly acknowledge the IIT computational plat-

form initiative for providing computer time. We

thank Grace Fox for editing and proofreading the

manuscript.

REFERENCES

Berman, H., Henrick, K., and Nakamura, H. (2003). An-

nouncing the worldwide protein data bank. Nat Struct

Biol, 10:980.

Besl, P. and McKay, N. (1992). A method for registration

of 3d shapes. IEEE Trans. on Pattern Analysis and

Machine Intelligence, 14:239–256.

Bicego, M., Dellaglio, F., and Felis, G. (2007). Multimodal

phylogeny for taxonomy: Integrating information

from nucleotide and amino acid sequences. J. Bioin-

formatics and Computational Biology, 5(5):1069–

1085.

Bottegoni, G., Rocchia, W., Rueda, M., Abagyan, R., and

Cavalli, A. (2011). Systematic exploitation of multi-

ple receptor conformations for virtual ligand screen-

ing. Plos One. in press.

Chen, Y. and Crippen, G. (2005). A novel approach to struc-

tural alignment using realistic structural and environ-

mental information. Protein Sci, 14:2935–2946.

Chen, Y. and Medioni, G. (1992). Object modeling by reg-

istration of multiple range images. Image Vision Com-

puting, 10:145155.

Duin, R. and Tax, D. (2000). Experiments with classiﬁer

combining rules. In Proc. Workshop on Multiple Clas-

siﬁer Systems, pages 16–29.

Favia, A. (2011). Theoretical and computational ap-

proaches to ligand-based drug discovery. Frontiers in

Bioscience, 16:1276–1290.

Fred, A. and Jain, A. (2005). Combining multiple

clusterings using evidence accumulation. IEEE

Trans. on Pattern Analysis and Machine Intelligence,

27(6):835–850.

Fumera, G. and Roli, F. (2005). A theoretical and experi-

mental analysis of linear combiners for multiple clas-

siﬁer systems. IEEE Trans. on Pattern Analysis and

Machine Intelligence, 27(6):942–956.

Hernandez, F., De Barreda, E., Fuster-Matanzo, A., Goni-

Oliver, P., Lucas, J., and Avila, J. (2009). The role of

gsk3 in alzheimer disease. Brain Res Bull, 80:248–

250.

Ho, T., Hull, J., and Stihari, S. (1994). Decision combi-

nation in multiple classiﬁer systems. IEEE Trans. on

Pattern Analysis and Machine Intelligence, 16(1):66–

75.

AN INNOVATIVE PROTOCOL FOR COMPARING PROTEIN BINDING SITES VIA ATOMIC GRID MAPS

421

Holm, L. and Sander, C. (1993). Protein structure compar-

ison by alignment of distance matrices. J Mol Biol,

233:123–138.

IUPAC (1997). Compendium of chemical terminology. (the

”Gold Book”). Online corrected version: (1994) ”Van

der Waals forces”.

Jain, A. and Dubes, R. (1988). Algorithms for clustering

data. Prentice Hall.

Jung, J. and Lee, B. (2000). Protein structure alignment

using environmental proﬁles. Protein Eng, 13:535–

543.

Kahraman, A. and Thornton, J. (2008). Methods to char-

acterize the structure of enzyme binding sites. In

Schwede, T. and Peitsch, M., editors, Computational

Structural Biology - Methods and Applications, vol-

ume 1, pages 189–221. World Scientiﬁc Publishing

Co.

Kawabata, T. (2003). Matras: A program for protein 3d

structure comparison. Nucleic Acids Res, 31:3367–

3369.

Kittler, J., Hatef, M., Duin, R., and Matas, J. (1998). On

combining classiﬁers. IEEE Trans. on Pattern Analy-

sis and Machine Intelligence, 20(3):226–239.

Kumar, A., Wong, D., Shen, H., and Flynn, P. (2003). Per-

sonal veriﬁcation using palmprint and hand geome-

try biometric. In Proc. of Int. Conf. on Audio and

Video-based biometric person authentication, pages

668–678.

Lorusso, A., Eggert, D., and Fisher, R. (1997). A compar-

ison of four algorithms for estimating 3-d rigid trans-

formations. Machine Vision Applications, 9:272290.

Mantel, N. (1967). The detection of disease clustering and

a generalized regression approach. Cancer Research,

27(2):209–220.

McLachlan, A. (1982). Rapid comparison of protein struc-

tures. Acta Cryst, A38:871–873.

Melnik, O., Vardi, Y., and Zhang, C.-H. (2004). Mixed

group ranks: Preference and conﬁdence in classiﬁer

combination. IEEE Trans. on Pattern Analysis and

Machine Intelligence, 26(8):973–981.

Morphy, R. and Rankovic, Z. (2006). The physicochemi-

cal challenges of designing multiple ligands. J Med

Chem, 49:4961–4970.

Morris, G., Huey, R., Lindstrom, W., Sanner, M., Belew, R.,

Goodsell, D., and Olson, A. (2009). Autodock4 and

autodocktools4: Automated docking with selective re-

ceptor ﬂexibility. J Comput Chem, 30:2785–2791.

Ross, A. and Jain, A. (2004). Multimodal biometrics: an

overview. In Proc. of European Signal Processing

Conference, pages 1221–1224.

Shindyalov, I. and Bourne, P. (1998). Protein struc-

ture alignment by incremental combinatorial exten-

sion (ce) of the optimal path. Protein Eng., 11:739–

747.

Tax, D., Breukelen, M., Duin, R., and Kittler, J. (2000).

Combining classiﬁers by averaging or by multiplying?

Pattern Recognition, 33:1475–1485.

Topchy, A., Jain, A., and Punch, W. (2005). Clustering en-

sembles: models of consensus and weak partitions.

IEEE Trans. on Pattern Analysis and Machine Intel-

ligence, 27(12):1866–1881.

Totrov, M. (2011). Ligand binding site superposition and

comparison based on atomic property ﬁelds: identi-

ﬁcation of distant homologues, convergent evolution

and pdb-wide clustering of binding sites. BMC Bioin-

formatics, 12(Suppl 1):S35.

Trucco, E. and Verri, A. (1998). Introductory Techniques

for 3-D Computer Vision. Prentice-Hall.

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

422