A TALE OF TWO (SIMILAR) CITIES

Inferring City Similarity through Geo-spatial Query Log Analysis

Rohan Seth, Michele Covell, Deepak Ravichandran, D. Sivakumar and Shumeet Baluja

Google, Inc., San Francisco, CA, U.S.A.

Keywords: Data mining, Spatial data mining, Log analysis, Large scale similarity measurement, Search engine queries,

Query logs, Census data.

Abstract: Understanding the backgrounds and interest of the people who are consuming a piece of content, such as a

news story, video, or music, is vital for the content producer as well the advertisers who rely on the content

to provide a channel on which to advertise. We extend traditional search-engine query log analysis, which

has primarily concentrated on analyzing either single or small groups of queries or users, to examining the

complete query stream of very large groups of users – the inhabitants of 13,377 cities across the United

States. Query logs can be a good representation of the interests of the city’s inhabitants and a useful

characterization of the city itself. Further, we demonstrate how query logs can be effectively used to gather

city-level statistics sufficient for providing insights into the similarities and differences between cities.

Cities that are found to be similar through the use of query analysis correspond well to the similar cities as

determined through other large-scale and time-consuming direct measurement studies, such as those

undertaken by the Census Bureau.

1 CENSUS & QUERY LOGS

Understanding the backgrounds and interest of the

people who are consuming a piece of content, such

as a news story, video, or music, is vital for the

content producer as well the advertisers who rely on

the content to provide a channel on which to

advertise. A variety of sources for demographic and

behavioral information exist today. One of the

largest-scale efforts to understand people across the

United States is conducted every 10 years by the US

Census Bureau. This massive operation, which

gathers statistics about population, ethnicity and

race, is supplemented by smaller surveys, such as

the American Community Survey, that gathers a

variety of more in-depth information about

households. Advertisers often use the high-level

information gathered by these surveys to help target

their ad campaigns to the most appropriate regions

and cities in the US.

In contrast to the Census studies, passive studies

of search engine query logs have become common

since the introduction of search engines and the

massive adoption of the Internet to quickly find

information (Jansen and Spink, 2006); (Silverstein

et. al., 1999). These studies provide the quantitative

data to not only improve the search engine’s results,

but also to provide a deeper understanding of the

user and the user’s interests than the data collected

by the Census and similar surveys.

The goal of our work is to extend techniques and

data sources that have commonly been used for on-

line single-user (or small group) understanding to

extremely large groups (up to millions of users) that

are usually only taken on by large studies by the

Census. We want to determine whether the query

stream emanating from groups of users – the

inhabitants of 13,377 cities across the United States

– is a good representation for the interests of the

city’s inhabitants, and therefore a useful characteri-

zation of the city itself. Figure 1 shows the geogra-

phic distribution of the queries analyzed in this study.

As a motivating example, consider whether by

examining the queries emanating from cities in

Silicon Valley, California could be automatically

determined to be similar to other technology centers

in the United States – for example in Redmond,

Washington or Cambridge, Massachusetts. Beyond a

city’s businesses, other factors, such as weather

patterns, socio-economic distributions, and

ethnicities, etc., play an important role in which

queries are submitted by a city’s denizens.

179

Seth R., Covell M., Ravichandran D., Sivakumar D. and Baluja S..

A TALE OF TWO (SIMILAR) CITIES - Inferring City Similarity through Geo-spatial Query Log Analysis.

DOI: 10.5220/0003641501710181

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 171-181

ISBN: 978-989-8425-79-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Geographic distribution of query samples used in

this study.

We show that by effectively combining location

information (at the city level) with search engine

query logs, we can ascertain the similarity of cities –

even those that may not be geographically close.

Finding similar cities provides a valuable signal to

advertisers and content creators. Once success (or

failure) is determined for the advertiser/content-

creator in one city, this analysis provides a basis for

setting expectations for similar cities – thereby

providing advertisers and content creators new cities

to target (or avoid). Additionally, knowledge of the

interests inherent in a city’s population provides

important information for tailoring search-engine

results to deliver results with a relevant local focus.

It is important to note that all of the signals used in

this paper can be discovered with minimal privacy

concerns – individuals do not need to be identified

and their individual search history need not be used.

As background, it should be pointed out that

there has been growing interest in utilizing

geography as a signal for returning search engine

results. Many search-engine query log analyses have

examined a user’s queries to better understand the

user’s interests and infer the user’s intent (Gan et al.,

2008); (Sanderson and Kohler, 2004); (Yi et al.,

2009). The hope is that by gaining this insight, the

search results returned to a user can be better

tailored to the user’s needs. Other studies have

combined the user’s IP location with the query to

determine what type of content the user may be

interested in (Hassan et al., 2009); (Jones et al.,

2008a) and also how to rank the search engine

results in light of strong geographic signals

(Andrade and Silva, 2006); (Jones et al., 2008b).

Systems to efficiently combine geographic relevance

with relevance as measured by more traditional

information retrieval measures have been developed

(Backstrom et al., 2008); (Chen et al., 2006). Often

geographic queries do not explicitly contain location

names. Nonetheless, by looking at the geographic

distribution of clicks or queries, the geo-sensitivity

of the query can be determined (Zhuang et al.,

2008a); (Zhuang et al., 2008b). Additionally, once

geo-intent is determined, language models specific

to geo-content or to a particular city can be

developed (Yi et al., 2009).

To analyze the massive set of queries required

for this study in order to determine city-level query-

streams, three problems must be overcome: (1)

extremely noisy query stream data: many queries

are mistakes, tests, or spam; (2) different city

population sizes: computer usage and access

patterns for cities make direct city comparisons

difficult; (3) “regression to the mean”: when

looking at aggregate level statistics, at a coarse level,

the diversity of people in each city lead effectively

to masking differences between cities within an

already diverse set of queries (i.e. all cities have a

large number of queries for “Twitter,” “Facebook,”

etc. and smaller amounts for “dog”, “topaz”, etc).

2 DATA COLLECTION

The analysis presented in this paper is based on

seven days of logs from Google.com gathered in

December, 2009. From this data, over 75 GB of

summary data was extracted, based on queries

originating in the United States. Based on the user’s

IP address that submitted the query, each query was

assigned a geographic “city-level” location, using a

database of IP-to-location mappings in conjunction

with the Google geocoder city-level “localities”

(discussed later), for a total of 13,377 distinct

locations. The accuracy of the IP-to-geographic

mapping varies depending on the location. In

particular, the number, layout, and size of the

internet service providers greatly affect the accuracy

of the mapping. The city-level locality is at a similar

accuracy level for many of the IP-address mappings.

We will refer to these 13,377 localities as Cities

Very simple pre-processing steps were employed

to clean the query stream. First, we normalized each

query by removing extraneous white spaces, special

characters, and capitalizations. Second, we discarded

any query that did not occur in at least 10 unique

cities. No more complex heuristics were employed.

Hereafter, the final set of unique queries will be

referred to as Q.

To begin this study, we first verified that

geography is a factor in query distributions

(Backstrom et al., 2008); (Zhuang et al., 2008a);

(Zhuang et al., 2008b). Figure 2 displays a few

example query distributions for terms that were

highly localized: “San Jose Mercury News,” and

“Northern Virginia Community College. (NVCC)”

NVCC appears almost exclusively in the northern

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

180

igure 2: Geographic localized queries. Top: Northern

irginia Community College. Bottom: San Jose Mercury

ews.

Figure 3: Non-localized queries. Top: “Christmas.

”

Bottom: “Google.”

parts of Virginia. “San Jose Mercury News” appears

in San Jose and surrounding towns, a bit in Los

Angeles, and a bit in New York – places commonly

associated with venture capital funding for startup

companies. In contrast, the geographic distribution

of other queries, for example those of a more general

interest, exhibit far less geographical coherence. A

few examples, “Google,” and “Christmas,” are

shown in Figure 3.

2.1 Ground-truth Data

There is no definitive measure of city-to-city

similarity. Often, simple measures such as

distribution of income levels, ethnicity, or education

level are used. However, each of these attributes

only captures a specific, small aspect of a city.

Rather than limiting our analysis to a single

dimension or risking introducing potential sources of

bias in our analysis by hand-selecting a single or

small set of attributes as our target, we took a more

comprehensive and automated approach.

We gathered over 750 city-to-city similarity lists,

based on information in the census-related surveys.

These lists only contained “the top 101” cities (and

counties) in the United States, in each of the 750

categories. List categories ranged from the expected

(population size, % of population with advanced

degrees, income level, etc.) to the obscure (largest %

of males working as cashiers, smallest percentage of

divorced people). Each list was used as a

component in our ground-truth calculations. To

create our ground truth similarities, we simply count,

for all pairs of cities, the number of lists in which

they co-occur. The end result is a “city-to-city”

association list that contains pairs of 12,873 unique

cities and counties. The highest-co-occurrence of

any two cities is 30. A wide range of cities is

included in these 12,873: for example, ranging in

population from 9.5 million (Los Angeles County

CA) to 95 (Indian Beach NC). This final list has the

advantage of measuring similarity across a large set

of dimensions and avoids testing biases introduced

by manually choosing a set of criteria.

Recall that this namespace of 12,873 cities and

counties have been generated by a completely

separate process than the logs analysis that generated

the 13,377 Cities

set. The set of 12,873 location

names are simply what was present on the 750 “top

101” lists that we used, derived the Census data.

The 13,377 Cities

set are based on the geo-coding

of the IP addresses we saw in the query logs that we

analyzed. As such, the names generally will not

match. We address this in Section 2.2.

While all 12,873 of city-to-city locations have

associations with 100 other cities (each list has 101

entries), many are only on a single list. This weak

information will be biased by which list that city was

listed on, which is what we are trying to avoid by

using 750 lists. To avoid this problem, we will only

consider as target cities for evaluation, those cities

that have at least one cohort city that shared lists

with them at least 3 times. This reduces the list of

“target cities” down to 8123 city-to-city locations.

We continue to use the full list of 12,873 as potential

partners to each target city, using the co-occurrence

to weight the associations and give more emphasis

to city pairs that occur more frequently.

2.2 Location Alignment

For reproducibility of our experiments, we provide a

A TALE OF TWO (SIMILAR) CITIES - Inferring City Similarity through Geo-spatial Query Log Analysis

181

detailed description of our location alignment

procedure. For readers not specifically interested in

implementing similar experiments, a skim of this

section will suffice.

As noted in the previous section, the ground-

truth and query-analysis results are built on two

separate namespaces. To try to bring the two

together, we passed each city-to-city name through a

geo-coder supplied by http://maps.google.com. Each

location was translated into latitude and longitude

coordinates. We then reverse geo-coded each of

these 12,873 latitude/longitude coordinates, mapping

each to the city-level “localities” used by

Google.com. These forward-reverse geo-coding

operations resulted in many-to-one assignments

from the 12,873 city-to-city lists to Google

localities. While all of these mapped into the Cities

set (for which we have query-log data), the mapping

was such that they mapped onto only 8093 Google

localities. Many-to-one mappings typically occurred

when counties from the city-to-city lists mapped to

the same locality as one of the also-referenced cities

within the county. In addition, we also saw within-

city neighborhood names from the city-to-city lists

mapping onto the same city-level locality.

To handle this ambiguity, we first consider how

we will evaluate the quality of our similarity results.

In Section 6, we provide a variety of analysis tools.

In all cases, we cycle through a list of target cities,

measuring for each our similarity results (given by

logs analysis) compared to what was given by the

ground truth (given by the city-to-city lists).

We define the “target city” as the city-to-city

location to which we want to measure or rank all the

known cities. In order to decide which Google

locality to use as the target city, we simply use the

forward/reverse geo-code mapping described above.

This gives us a pair of vectors to compare: one from

the city-to-city namespace, containing sparse

mappings within a set of 12,872 other city-to-city

names and the other from the Google locality

namespace, giving us a dense mapping to 8093 other

Google localities that are their geo-coding-based

“partners.” Note that, based on the list occurrence

requirements mentioned in the previous subsection,

there are 8123 target cities, which then map onto

only 4478 Google localities. The full 8123-target set

is distinct since the target city data is evaluated as a

pair and the city-to-city sparse mappings will be

different for each of the 8123 names, even when the

query-analysis mappings are repeated by the many-

o-one nature of the association.

For each of these target cases, we need to

compare a sparse association mapping into the

12,872 city-to-city namespace with a dense mapping

into the 8093 Google query-stream localities. For

many Google localities, there is only one city-to-city

name with a default mapping onto that Google

locality name. We fix these mappings as our first

step. For the remaining Google localities, where the

association to a city-to-city name is ambiguous, we

use an optimistic mapping onto city-to-city names

that have not already been used. The greedy

mapping starts from the most strongly associated

Google locality (in the ambiguous set) and picking

(from the city-to-city set within the 30km radius) the

most strongly associated city-to-city name that has

not already been used.

This mapping is used in all evaluations,

including the baseline orderings by geographic

distance, total population, and population difference

(Section 6). Despite this bias to closer alignments,

by looking at relative performance where all

alternatives share the same optimistic advantages,

we avoid overstating results in any direction.

3 FEATURE SPACE

One of the difficulties in comparing queries, even

after standard normalization steps are taken, is that

queries that may initially appear to be far apart, in

terms of spelling and edit distance, can represent the

same concept. For example, the terms “auto” and

“cars” are often used interchangeably, as are “coke”

and “pop” or “mobile” and “phone.” To treat these

sets of queries as similar, we replace each query

with a concept cluster.

Concept clusters are based on a large-scale

Bayesian network model of text, as detailed in

(Datta, 2005); (Harik and Shazeer, 2004). Datta

describes the creation of PHIL (probabilistic

hierarchical inferential learner). Although a full

explanation of the PHIL system is beyond the scope

of this paper, a cursory overview is provided here.

PHIL is a top-down weighted directed acyclic graph

in which the top node represents “all concepts” and

the leaf nodes represent individual words or

compound-word tokens. The intermediate nodes,

which can be learned through word co-occurrence

statistics over large text corpora, are created

automatically. The intermediate nodes contain many

conceptually similar words. PHIL was originally

used as a generative model of text. For our

purposes, each query is used as input to the system,

and the intermediate nodes that are most highly

activated are assigned to the query. Similar concept

queries will activate similar nodes. Interestingly, this

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

182

system not only helps account for different words

often used to represent the same concept (e.g.,

autos/cars) but it also helps to automatically correct

for common spelling mistakes: the same nodes will

be activated for common variations of the same

word.

In Section 6, we will empirically compare the

use of terms and PHIL clusters as the underlying

features for our system.

4 A CITY’S QUERY SIGNATURE

For each city, we need to compute a signature vector

that will be used to compare with the signature of

other cities. In addition to the choice between query

terms and query concepts, described in the previous

section, we must consider purely descriptive versus

discriminative signature vectors.

The simplest signature is a (descriptive)

histogram of the queries that originated from the

city. This has a straightforward computation: for

each unique query (whether term or concept), q, that

occurs from any city in our collected set, Q, we

count how many times the query originated from a

city, c. Each city is assigned a vector of integers, of

length |Q|. Many smaller cities will have numerous

zero entries; these indicate that the query never

occurred in the city during the sampling time. The

histogram is normalized so that each query’s entry

reflects the percentage of the total query volume the

query accounts for.

A limitation of this simple histogram approach is

seen in many descriptive signatures: it may place

emphasis on non-interesting portions of the query-

space. For example, we expect that a common query

such as ‘pizza’ will occur far more often than a

query such as ‘babaganoush,’ or that ‘blue-ray’ will

be far more numerous than ‘cassette tape.’ The fact

that these relations repeatedly hold in almost every

city is neither interesting nor surprising when trying

to find how cities differ. Rather, the converse is true:

when these relations do not hold is when the data is

interesting.

To draw attention to the surprise features of a

city, we use a simple discriminative scheme that is

analogous in spirit to the family of TF-IDF (Salton

and McGill, 1983) procedures commonly employed

in information retrieval tasks. We call the measure

an excess score. Intuitively, the goal of an excess

score is to determine how much above (or below)

each query was from the expected. We determine

how much we expected to see a query by treating the

entire set of queries from all cities (Cities

) as a

single city, and computing the distributions of

queries in this aggregated set. Specifically, it is

computed as follows. First we compute the expected

volume of the query averaged across all cities. This

percentage becomes our expectation for that query:

expectedPercentage

query

Volume

c,query

c ∈Cities

∑

Volume

c,q

q ∈Q

∑

c ∈Cities

∑

Using the expected percentage, we compute how the

query volume in a city differed from the percentage

we expected from that city, given its total volume:

excess

query|city

Volume

city,query

Volume

city,q

q ∈Q

∑

− expectedPercentage

query

Four points should be made about the excess score.

First, as shown above, it calculated the “surprise

factor” of each query per city – it does not represent

the volume directly. Alternatively, we could have

simply modified the calculation to find the excess

cities for each query – i.e., for each query, find

which cities had a higher (or lower) than expected

occurrence of that query. First we compute the

expected query volume of a city, averaged across all

queries, and then we estimate that city’s expected

percent contribution to the total number of queries

examined in the study.

expectedPercentage

city

Volume

city,q

q ∈Q

∑

Volume

c,q

q ∈Q

∑

c ∈Cities

∑

excess

city|query

Volume

city,query

Volume

c,query

c ∈Cities

∑

− expectedPercentage

city

Second, it should be noted that the excess scores

can be negative. Intuitively, for the cities that have a

negative excess score for a query, in that city, the

query may have occurred less than expected.

Third, the excess score for the queries for any

city should sum to 0.0. The fact that some query

occurred more times than expected implies that

some other query (or set of queries) must have

occurred less than expected when looking at that

same volume of queries.

Fourth, for simplicity, we calculated the

expectation as the ‘global expectation,’ using all the

cities in Cities

. An alternative is to compute more

specific expectations, such as using only the nearest

n-cities, or dividing the U.S. into quadrants, etc.

A TALE OF TWO (SIMILAR) CITIES - Inferring City Similarity through Geo-spatial Query Log Analysis

183

5 SIMILARITY COMPUTATION

Given the excess metrics as well as the simple

percentage based signatures, described in the

previous sections, we need to decide how to

compute the distance between two cities. We

consider two alternative methods. The first method

is the standard cosine similarity, with the excess

vectors and the percentage based vectors.

A second similarity metric is based on the excess

scores for a city given a query (

excess

city|query

). For

this calculation, we examined every query in Q.

For each query, q, cities were assigned their excess

score and the list was sorted. This sorted list

represented which cities had the highest (positive)

“surprise factor” for q, taking into account their

expected total volume. From each list, all cities that

co-occurred within the top-10 query excess scores

had their similarity score incremented. Intuitively,

this measures how many times each pair of cities

coincided on having more than expected query

volumes for a particular query. We refer to this

similarity measure as “reverse-occurrence voting”.

The problem with reverse-occurrence voting is

that there is no guarantee that every city will be

voted for, even once, by the query set that was seen.

Even with more than 12 million distinct query terms,

some cities (typically small ones) never rise to the

top 10 of even a single query list. Nearly one fourth

of our target cities suffered from this anonymity. As

can be seen in Figure 4, even those cities that did

make it to some type of characterization were more

poorly described by the reverse-occurrence voting

than by the cosine similarity.

In Figure 4, we show a comparison of the

performance of cosine similarity and reverse-

occurrence voting, where both measures were taken

over only the target cities that were not anonymous

under reverse-occurrence voting (just over 6000

city-to-city names). The figure shows the

performance for all four combinations from Sections

3 and 4: query terms or PHIL clusters with excess or

percentage scores. The graph shows how many of

the top-10 most strongly connected cities were

retrieved using cosine similarity versus reverse-

occurrence, according to the retrieval-set size. The

retrieval set is taken from the ordering of most-to-

least similar cities given by each of the two alternate

measures. In Figure 4, the x-axis is the size of the

retrieval set (as a % of the full 8093 possibilities)

and the y-axis is the average recall rate for these top

city-to-city localities, averaged across the non-

anonymous target cities. The average retrieval using

cosine similarity is, for this one graph, also averaged

on this reduced set of cities that was not anonymous

under reverse-occurrence voting.

Figure 4: Using cosine similarity vs. reverse-occurrence

voting. The average retrieval rates for the top-10 matches

for each city when retrieving N% (x-axis) of the cities –

ordered by similarity. For example, when cosine distance

is used and 1.5% of the cities are retrieved, approximately

43% of the top-10 most similar cities are included. With

reverse occurrence, only 20-24% of the top-10 closest

cities are included. This lower performance is true whether

we use query terms or PHIL clusters and whether we use

excess or percentage features.

Not only does reverse-occurrence voting leave

many cities completely uncharacterized, but it also

provides only about half of the recall rate, compared

to cosine similarity, for the same size retrieval set.

For this reason, the remainder of this paper uses

cosine similarity on the query vectors (query terms

or PHIL clusters in excess scores or percentages) to

determine city similarities.

6 EXPERIMENTS

As discussed in Section 2.2, our method for mapping

city-to-city names onto Google locality names will

tend to bias our evaluations towards aligning our

similarity lists to be more in agreement with the city-

to-city lists. As a result of this systematic bias, we

need to separately measure the improvement

provided the optimistic name remapping and remove

it from our evaluation results. Throughout this

section, we match the bias-removal method to the

summary statistic being shown.

One summary statistic that we provide is the

weighted connected similarity: measured from each

target city to all of the cities with which it co-

occurred in the city-to-city lists, it is the cosine

similarity, weighted by the shared-list count. We

correct this simple statistic using two factors. The

first corrects for the similarity that each target city

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

184

shows to all known cities. The second corrects (on

average) for the bias introduced by the optimistic

namespace mapping. By correcting for both, we can

interpret a zero offset similarity as being equivalent

to random selection of neighbor cities.

Figure 5 shows the histograms of the first

correction factor: for each target city, what similarity

its query vector showed, on average, with the query

vectors of all of the other known cities. There is a

very strong positive similarity seen in all of our

query-based similarity measures for our locality set.

This strong positive average similarity across all of

our known localities is easy to understand for the

percentage measures: all of the values for the

percentage features will be positive, since all

percentages are positive, so measuring cosine

similarity on these vectors will always give a

positive result.

Figure 5: Histogram of the average similarity, from each

target city to all known cities. The strongly positive biases

show that the query vectors, whether terms or clusters,

percent or excess, vary across our localities in strongly

correlated ways.

The even stronger positive similarity seen in the

excess measures shows that directions of variations

in the underlying percentages are also strongly

aligned: even taking a differential measure of the

per-location query vectors does not scatter these

vectors uniformly across the vector space. High

positive average similarities limit the offset

similarity that we can achieve: that is, the weighted

similarity of the linked cities relative to (or offset

by) this all-city average. Even so, high positive

average similarities suggest that our excess scores

are not measuring noise only: our query vectors do

contain a lot of related entries that should show

synchronized variation, which will remain even after

taking the excess score.

The second correction factor is a further offset to

the similarity score to, on average, reduce the effect

of the optimistic namespace mapping that we are

doing. For each type of query vector (term or PHIL,

excess or percentage), we looked at the scores of all

the cities available for any of the ambiguous

namespace mappings that were within the 30 km

radius of an ambiguous Google locality. Within

each of these 30 km sets, we measured the standard

deviation in the similarity score and then took the

average of all these standard deviations, across all of

the sets. This gives us an average measure of how

optimistic our namespace mapping will tend to be,

according to the query vector type. Since these

localized standard deviations are not the same for

the different query-vector representations, we need

to reduce the offset similarity scores by these

representation-dependent amounts before

comparison. For the four different query

representations, these corrections reduced our

reported offset similarity: for percentage query terms

and PHIL clusters, by less than 0.01; for excess

PHIL clusters, by 0.06; and for excess query terms,

by 0.13. Our histograms, shown in Figure 6, have

had their offset similarity scores reduced by these

amounts before plotting.

Based on Figure 6 (left and center), the excess

score is more accurate than the percentage scores in

finding similar cities. The excess scores are nearly

always doing better than simple random association,

as shown by the excess bars (yellow) being 100% of

the target cities above the zero offset-similarity

score. In contrast, only 58% and 60% of the target

cities are doing as well or better than random, using

percent PHIL clusters and percent query terms,

respectively. Based on this weak result for the

percentage terms, we do not consider it further.

Figure 6 (right) suggests that the excess-PHIL vector

is giving a stronger similarity signal than are the

excess-term vector: the excess-PHIL vector has

nearly 50% of the target cities at or above an offset

similarity score of 0.3, while the excess-term vector

has only 10% of the target cities at or above that

level. However, since we have not adjusted these

two offset-similarity populations for differences in

dynamic range, we cannot draw any substantive

conclusion from this comparison. Normalizing by

the standard deviation will not help, since the

excess-term vector similarities form a super-

Gaussian (heavy-tailed) distribution while the

excess-PHIL vector similarities give a sub-Gaussian

(weak-tailed) distribution.

In order to further evaluate the relative

performance of excess-PHIL and excess-term

vectors, we look at the detailed recall behaviors of

the two approaches. We do this, for each target city,

by looking for 10 cities that were most strongly

A TALE OF TWO (SIMILAR) CITIES - Inferring City Similarity through Geo-spatial Query Log Analysis

185

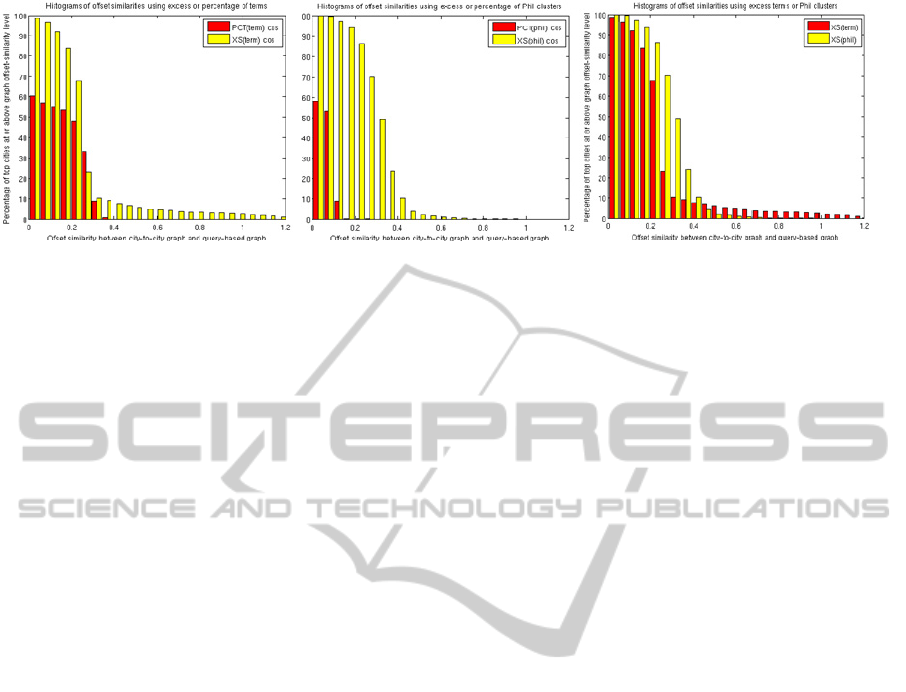
Figure 6: Offset similarity histograms. Weighted-average similarity from each target city to their city-to-city connected

localities, offset by the average similarity of that target city to all known localities. Left and center: excess-based

representations do better than the corresponding PHIL-based representations. Right: the excess-PHIL representation does

better than the excess-term.

associated with that target city in the city-to-city

lists, within the list of known cities, as ordered by

the query-analysis similarity. For example, for

Cambridge MA, we would look for Berkeley CA,

Stanford CA, Brookline MA, Somerville MA,

Boston MA, Albany CA, New York NY, Hanover

NH, Ithaca NY, and Bethesda MD, based on the

city-to-city lists. We would then count how many of

these 10 cities were among the top 0.1% (10 of

8096) , 0.2% (20), 0.4% (30), 0.5% (40), 0.7% (60),

1% (80), 1.5% (120), and 2% (160). Continuing

with our Cambridge MA example, using the excess-

term vectors to order our retrieval results, we see

four of these top cities in the first 10 results (namely,

Boston, Brookline, New York, and Bethesda), 5

cities in our first 20 results (adding in Stanford), 6

cities in our first 30 results (adding in Somerville), 7

cities in our first 40 results (adding in Ithaca), 8

cities in our first 60 results (adding in Hanover), and

9 cities in our first 80 results (adding in Berkeley).

The tenth city (Albany) does not occur in our

retrieval results until position 212, so it is not

included in our reported results.

When we do this more detailed evaluation of the

most-similar recall rates, the differences in recall

rates between excess-PHIL and excess-term are not

significant. Excess-PHIL processing gives, on

average, 1.5% to 2% better recall than excess-term

across the considered retrieval sizes (where recall of

all 10 top cities corresponds to 100% recall).

Excess-term does better than excess-PHIL on large

cities while excess-PHIL does better on mid-sized

and small cities. However, the standard deviation in

these recall differences are on the order of 12% to

15% and none of these differences even approach

statistical significance. Based on this lack of

significance, we only show the results of the excess-

term vector for the remainder of this paper.

Figure 7 shows the details of our recall results,

across retrieval-set size, for all target cities. The x

axis is the retrieval set size. The different colors in

stacked bar graphs at each x position show how

many of the sought-after 10 cities were seen at that

retrieval size and the size of each colored section

show what percentage of the target-city set got that

level of recall, at that retrieval size. Returning to our

Cambridge example, this city would be included in

the “4” color region, at the 0.1% retrieval size (with

higher recall than 79% of the other target cities at

that retrieval size); in the “5” color region, at the

0.2% retrieval size (better than 78% of the target

cities); in the “6” color region at 0.4% recall (better

than 81% of the target cities); in the “7” color region

at 0.5% recall; and so on.

We again need to provide a baseline result

against which to compare. While it is tempting to

compare to random sampling without replacement,

that comparison is too optimistic due to our

namespace mapping process. Instead, in Figure 8,

we show three baseline orderings: by distance, by

population size, and by population difference. For

our distance ordering, for each target city, we sort all

known cities according to their distance from the

target. This is based on the hypothesis that places

that are near each other are most similar. After we

have done this initial sort, we repeat the same

namespace mapping as was described in Section 2.3,

so the distance mapping can receive the same boost

to its recall results. Our second baseline ordering is

by population size. We sort all known cities once,

according to their reported population size (largest to

smallest). We use this single ordering as a starting

point for all target cities but allow it to be modified

for the ambiguous names, again using the mapping

described in Section 2.3. Our final baseline ordering

is by population difference. For each target city, we

sort all known cities, according to their (absolute)

population difference compared to that target, so that

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

186

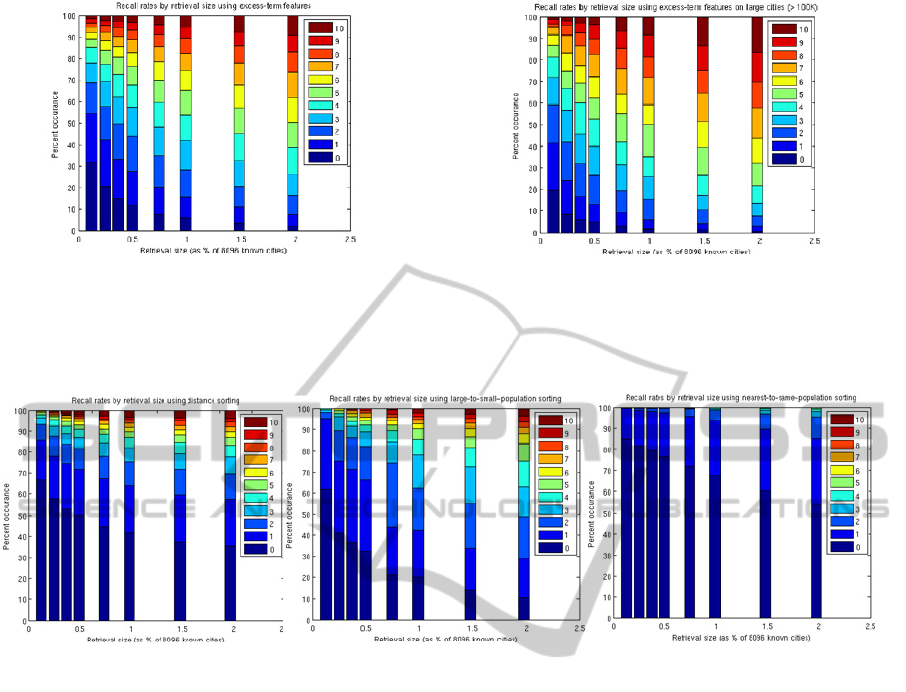
Figure 7: Recall rates, by retrieval-set size, using excess-term features. Each bar show the recall distribution, across

target cities, attempting to find the top 10 city-to-city associations in the retrieval result provided by excess-term similarity

sorting. The colors correspond to different recall rates, from finding all 10 cities (top, red) to finding none (bottom, blue-

black). The X-axis is the retrieval-set size, as a % of the full set of 8096 known cities, ranging from 0.1% up to 2%. Left:

the results across all target cities. Right: the results on large cities (> 100K population).

Figure 8: Recall rates, by retrieval-set size, using three baseline methods. These graphs provide baseline performance

levels for the recall according to retrieval-set size. Left: Using geographic distance to sort known cities. Middle:

population size (from largest to smallest). Right: we use the difference in population size compared to the target-city size

(from closest in size to most different).

cities that are of similar size to the target will occur

early in the list and cities that are much larger or

smaller will occur late in the list. We again use the

namespace mapping from Section 2.3.

As can be seen by comparing Figures 7 and 8,

the recall results for the excess-term-based sorting

are much higher than what would be provided by

any of our simple baseline methods. Since the

baseline methods enjoy the same optimistic

namespace mapping as our excess-term results, our

results are not due to that mapping. In Figure 7, we

can also see an improvement from the average

target-city recall performance to that of the largest

target-city recall.

For an intuition of the derived similarities, we

look at the results from two well-known, mid-sized,

locations: Cambridge, MA and Redmond, WA.

Cambridge is the home of two prestigious

universities (MIT and Harvard), as well as being a

center for high-tech startups and defense contracting.

When we look at the top associated cities, the first

three associated localities share some of these

characteristics but most likely are listed due to

geographic location: Boston MA, Brookline MA,

and Waltham MA are all very close to Cambridge.

In addition to those nearby cities, we see

associations that are best explained by character:

Palo Alto CA has a high quality university

(Stanford), as well as many high-tech companies,

both start-up (Facebook, VMware, etc) and

established (Hewlett-Packard, Xerox PARC, Fuji-

Xerox Research). There is a cluster of associated

cities from the defense-contractor centers:

specifically, Bethesda VA, Arlington VA, and Fort

Myer VA. The association with Irvine CA is may be

due to its mix of academics (UC Irvine) and high

tech (Broadcom). Bellevue WA is also closely

associated, probably since it is near Microsoft.

Similar types of associations can be seen for

Redmond WA (Microsoft Headquarters). Two

nearby communities are most strongly associated:

Seattle WA and Bellevue WA. There is a cluster of

cities from the Boston area, which share the high-

tech bias: namely, Cambridge MA, Waltham MA

A TALE OF TWO (SIMILAR) CITIES - Inferring City Similarity through Geo-spatial Query Log Analysis

187

(with many high-tech start ups), and Lexington MA

(with MIT Lincoln Labs). The largest group of

associated cities for Redmond is from the Silicon

Valley area: Sunnyvale CA, San Jose CA, Mountain

View CA, and San Francisco CA. In addition,

Buffalo NY (with SUNY) and Oakland CA (with

Berkeley) are associated with Redmond, probably

based on their engineering schools.

7 CONCLUSIONS

In this paper, we have employed techniques that

have previously been used to examine either single

or small sets of users and extended the procedures to

analyze the populations of more than 13,000 cities

across the U.S. Despite the diversity of people in

cities, we are able to find signals in the aggregate

query streams emanating from the cities and use

them to determine similar cities that are not

necessarily geographically close.

The most important signal we used for our

analysis, the excess score, was both simple and easy

to compute. Intuitively, it measures the ‘surprise’ in

the volume of a particular query. This measure helps

us overcome two important difficulties with the data.

First, every city has many queries for common

terms; instead of simply eliminating these common

terms (as is often done with stop-list type

approaches), the effect of these terms is reduced

unless there is a reason to pay attention to the terms

(i.e. they occur either more or less than expected in a

city). Second, the excess measure also provides a

simple basis with which to normalize for the query

volume of a city. This was crucial, considering the

wide range of population sizes and search engine

usage in the cities examined.

The results obtained by our system perform well

even with small retrieval sets. With only retrieving

160 cities (2% of the known cities), on average, we

find 6 cities from the top-10 closest cities (measured

by the census-data-based city-to-city dataset). Other,

intuitive heuristics, such as geographically closest

160 cities, or 160 cities with the closest sized

population, performed significantly worse.

There are a number of future directions for

exploration. In terms of the algorithms, one of the

first experiments to conduct is with weighted excess

metrics. Currently, each term is normalized such

that its contribution is proportional to its deviation

from its expected volume. However, some terms

may be more important than others – for example, if

a term that was expected to account for a large

percentage of a the query traffic didn’t (i.e. there

was only 1/10

the number of expected queries of a

popular term like “Twitter”), that may be more

telling about the population than the drop of a less

popular term (i.e. 1/10

the volume of the query

“Pinto muffler”). One simple method to incorporate

an importance weighting is to multiply the excess

score with the query’s expected percentage of

traffic. Experiments need to be conducted to see

whether such a weighting translates into improved

performance.

In this paper, we attempted to find similar cities

by looking at their query distributions.

Alternatively, we could also address the task of

finding related queries by looking at their excess

distributions across cities.

Beyond comparing directly to Census data,

perhaps most important to large scale adoption of

this work, we need to measure how the similar-city

lists found here correlate with the success and failure

of content and advertising campaigns that have been

launched in multiple cities. Understanding this, first

through historical log analysis and then through

controlled trials, will be an important step towards

understanding the extent to which the city-

similarities can be used for helping content-creators

and advertisers.

REFERENCES

Andrade, L. and Silva, M.J. (2006). “Relevance Ranking

for Geographic IR.” In Proc. ACM SIGIR Workshop

on Geo.Information Retrieval

Backstrom, L., Kleinberg, J., Kumar, R., and Novak, J.

(2008). “Spatial Variation in Search Engine Queries.”

In Proc. International Conference on World Wide Web

pp. 357-366.

Y. Chen, T. Suel, and A. Markowetz (2006). “Efficient

Query Processing in Geographic Web Search

Engines.” In Proc. ACM SIGMOD Int. Conference on

Management of Data pp. 277-288.

Datta, R. (2005) “PHIL: The Probabilistic Hierarchical

Inferential Learner,” 10

Annual Bay Area Discrete

Mathematics Day. http://math.berkeley.edu/

~datta/philtalk.pdf

Gan, Q., Attenberg, J., Markowetz, A., and Suel, T.

(2008). “Analysis of Geographic Queries in a Search

Engine Log.” In Proc. ACM International Workshop

on Location and the Web pp. 49-56.

Harik, G., Shazeer, N. (2004) “Method and Apparatus for

Learning a Probabilistic Generative Model for Text,”

U.S. Patent 7231393.

Hassan, A., Jones, R. and Diaz, F. (2009). “A Case Study

of using Geographic Cues to Predict Query News

Intent.” In Proc. ACM SIGSPATIAL International

Conference on Advances in Geographic information

Systems pp. 33-41.

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

188

Jansen, B.J., and Spink, A. (2006). “How are We

Searching the World Wide Web? A Comparison of

Nine Search Engine Transaction Logs.” Info.

Processing and Management 42 (1): 248-263.

Jones, R., Zhang, W.V., Rey, B., Jhala, P., and Stipp, E.

(2008a). “Geographic Intention and Modification in

Web Search,” Int. J. Geographical Information

Science. 22 (3): 229-246.

Jones, R., Hassan, A., and Diaz, F. (2008b). “Geographic

Features in Web Search Retrieval.” In Proc.

International Workshop on Geographic Information

Retrieval (Napa Valley, CA), pp. 57-58.

Salton. G. and McGill, M.J. (1983). Introduction to

Modern Information Retrieval. McGraw-Hill.

ISBN 0070544840.

Sanderson, T. and Kohler, J. (2004). “Analyzing

Geographic Queries.” In Proc. ACM SIGIR Wkshp on

Geo. Info. Retrieval

Silverstein, C., Marais, H., Henzinger, M., and Moricz, M.

(1999). “Analysis of a Very Large Web Search Engine

Query Log.” SIGIR Forum 33 (1): 6-12.

Yi, X., Raghavan, H., and Leggetter, C. (2009).

“Discovering Users' Specific Geo Intention in Web

Search.” In Proc. International Conference on World

Wide Web (Madrid, Spain), pp. 481-490.

Zhuang, Z., Brunk, C., and Giles, C.L. (2008a). “Modeling

and Visualizing Geo-Sensitive Queries based on User

Clicks.” In Proc. ACM International Workshop on

Location and the Web, pp. 73-76.

Zhuang, Z., Brunk, C., Mitra, P., and. Giles C.L (2008b).

“Towards Click-Based Models of Geographic Interests

in Web Search.” In Proc. IEEE/WIC/ACM

International Conference on Web Intelligence and

Intelligent Agent Technology pp. 293-299

A TALE OF TWO (SIMILAR) CITIES - Inferring City Similarity through Geo-spatial Query Log Analysis

189