OPTIMIZATION OF STRUCTURE OF FUZZY-NEURAL

SYSTEMS USING COEVOLUTIONARY ALGORITHM

Zikrija Avdagic, Samir Omanovic, Emir Buza and Belma Cardakovic

Department for Computer Science and Informatics, Faculty of Electrical Engineering in Sarajevo,

Zmaja od Bosne bb, Kampus Univerziteta, 71000, Sarajevo, Bosnia and Herzegovina

Keywords: Coevolutionary algorithm, Fuzzy logic, Neural network, Mamdani fuzzy system, Hybridization.

Abstract: This paper is related to a research of modelling fuzzy-neural systems using the coevolutionary algorithm,

and has the focus on advantages of using the coevolutionary algorithm for system structure optimization. In

the context of this work, the term fuzzy-neural system defines the system that can be used as the fuzzy

system with all its functionalities or as the neural network with all its functionalities. The hybridization of

fuzzy logic, neural networks and coevolutionary algorithm and its architecture are presented in general, and

the role of the coevolutionary algorithm in structure optimization is described in details. Results of testing

with Iris Database, from UCI Machine Learning Repository are also presented. Tests performed during the

research supports the conclusion that usage of the coevolutionary algorithm for the fuzzy-neural system’s

structure optimization is very efficient.

1 INTRODUCTION

This paper presents current results in research of

modelling fuzzy-neural systems using the

coevolutionary algorithm, based on the novel

hybridization of fuzzy logic, neural networks and

coevolutionary algorithm. Focus of this paper is on

advantages of usage of the coevolutionary algorithm

for fuzzy-neural system’s structure optimization. In

the context of this work, the term fuzzy-neural

system defines the system that can be used as the

fuzzy system with all its functionalities or as the

neural network with all its functionalities. In this

hybridization, the coevolutionary algorithm is used

as the primary mechanism for model optimization,

while specific backpropagation (Omanovic and

Avdagic, 2011) is used as the secondary mechanism

and is not explained here in details.

Basically, there are two main approaches in

using coevolutionary algorithm. In the first approach

coevolving species are complete models, while in

the second approach coevolving species are parts of

the one model. The hybridization used in this

research uses the second approach where coevolving

species are parts of the one model. There are similar

usages of the coevolutionary algorithm like the

coevolutionary fuzzy modelling (Pena-Reyes, 2002).

There are many other approaches in combining soft

computing techniques that do not use coevolutionary

algorithm, but have the same purpose (see Abraham,

2005; Kasabov, 2003; Cordón, 2001; Chen and

Abraham, 2010; and many others).

Each approach has its advantages and

disadvantages and this hybridisation try to use

advantages of the cooperative coevolution. The main

idea of the cooperative coevolution is that species

are helping each other in achieving the common

goal. The most important aspect of applying the

coevolutionary algorithm is creating the species in

the way that the model’s structure breakdown is

performed based on logical meanings of structure

elements.

2 COEVOLUTIONARY

ALGORITHM APPLICATION

The fuzzy-neural system’s structure and its logical

breakdown to ++2 coevolving species are

presented on Figure 1, where  is the number of

input fuzzy variables and  is the number of

membership functions of the output fuzzy variable.

125

Avdagic Z., Omanovic S., Buza E. and Cardakovic B..

OPTIMIZATION OF STRUCTURE OF FUZZY-NEURAL SYSTEMS USING COEVOLUTIONARY ALGORITHM.

DOI: 10.5220/0003642001250130

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 125-130

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

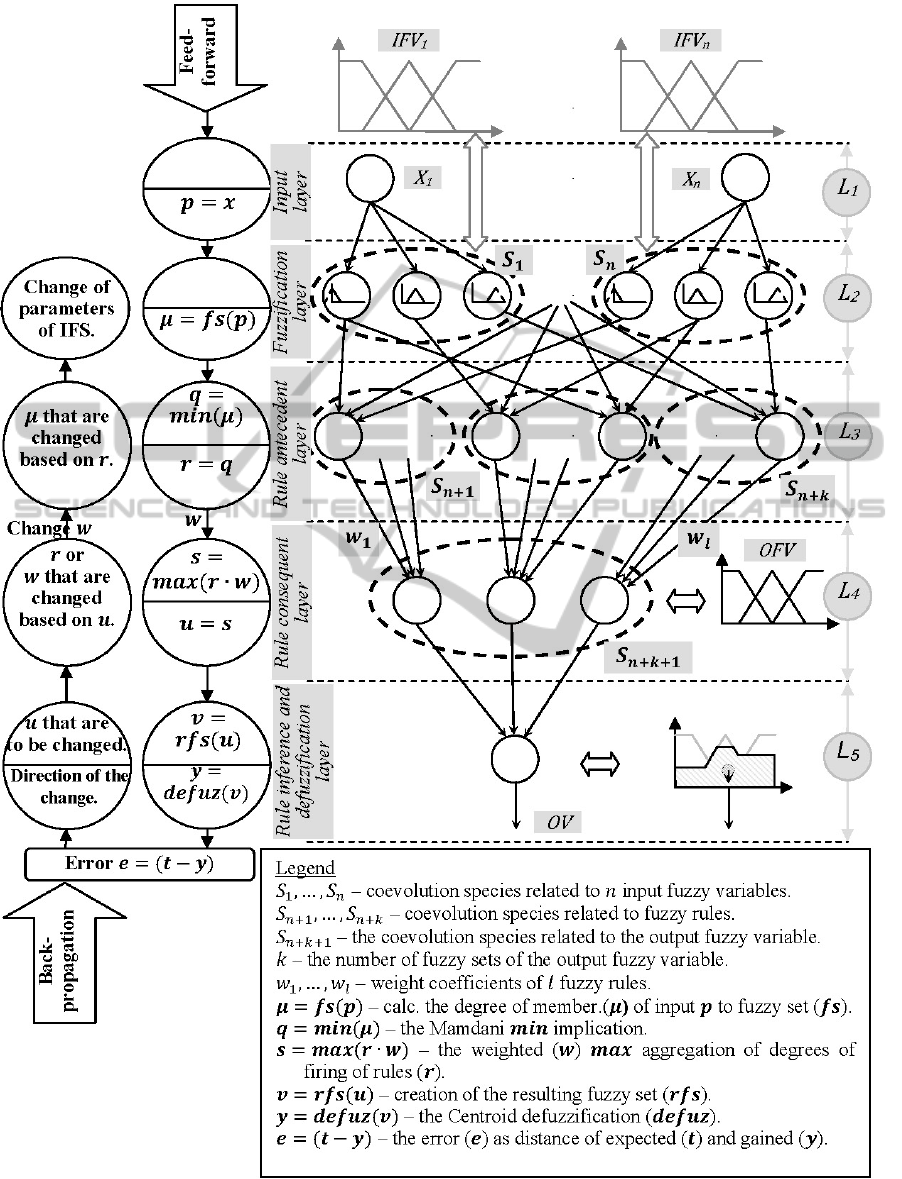
Figure 1: Architecture of the hybridization.

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

126

As can be seen on Figure 1, fuzzy system and

neural network have a full structure mapping.





,…,



are species related to input fuzzy variables,

where one species have a chromosome that contains

all nodes (i.e. membership functions parameters)

related to one input fuzzy variable. 



,…,



are

species related to fuzzy rules. Antecedent parts of

rules with the same consequent part are encoded in

the same chromosome. Since the number of different

consequent parts is equal to the number of

membership functions in output fuzzy variable,

number of species related to fuzzy rules is equal to

the number of membership functions of the output

fuzzy variable. Chromosome for the species 



is composed of nodes (i.e. membership functions

parameters) of the output fuzzy variable. The last of

species – 



is related to active/inactive rules in

the model. This species is not marked on Figure 1

because it cannot be done in adequate way.

Chromosome size in each of species is variable

during the evolution of that species, because the

number of membership functions per fuzzy variable

and number of rules are changed dynamically.

From the rough description of the coevolving

species is possible to see that structure of the fuzzy-

neural system is split to coevolving species based on

logical interrelationships of elements. This is very

important for the coevolution efficiency, which is

shown in the tests results.

2.1 General Characteristics of the

Hybridisation

Hybridisation presented on Figure 1. uses only

triangular fuzzy sets. Fuzzy system is of Mamdani

type. Defuzzification type is centroid. The neural

network is five-layered with a clear mapping of the

fuzzy system into the neural network. The specific

backpropagation, not explained in details here, used

in this hybridisation can perform small adaptations

of the fuzzy-neural system and can be used after

system is built. Although the main optimization

mechanism is coevolutionary algorithm,

backpropagation is used partially during system

building. These two mechanisms interleave during

system’s model optimization as global and local

mechanism.

These characteristics are chosen to support

following goals:

 Fuzzy presentation of knowledge learned, that

enables its easier interpretability;

 Smaller size of the resulting fuzzy system’s model

comparing to Sugeno since “the number of the input

fuzzy sets and fuzzy rules needed by the Sugeno

fuzzy systems depend on the number and locations

of the extrema of the function to be approximated”

(Sivanandam et all, 2007);

 The resulting system can be used as fuzzy system

with all its functionalities or as neural network with

all its functionalities including the backpropagation.

2.2 Coevolution Characteristics

From the previous explanation of the species that are

in coevolution it is obvious that complexity of the

optimization problem is high. Besides that,

implementation this hybridisation generates the

fuzzy-neural system from data automatically, which

additionally makes the problem more difficult. But

this coevolution organization has species with

relatively small chromosomes comparing to similar

cases where less species is used for fuzzy system’s

model optimization.

Each optimization algorithm has its mechanisms

to skip local optimums and search for better

solution. In the case of this hybridization, the

coevolutionary algorithm is implemented with

following mechanisms and with following

behaviours:

 Coevolution of species. Coevolution of species is

implemented in the classical manner where each of

species has its own evolution up to the fitness

calculation. For fitness calculation, target member

and chosen cooperators from the rest of the species

are joined to form fuzzy-neural system. That fuzzy-

neural system (as neural network) is shortly trained

via the specific backpropagation to increase the

quality of the model and to measure its performance

with the training dataset. Behaviour of the

coevolution of species mainly depends on input

parameters, but also on additional mechanisms:

In the case of the very weak progress mechanism

of random generation of members is used along with

the basic mechanisms – crossover and mutation.

In the case of the weak progress, some of parameters

of the coevolution are change dynamically.

 Coevolution of two groups of species. This type of

coevolution is based on the analogy with the

coevolution of two species in coevolutionary fuzzy

modelling (Pena-Reyes, 2002). While in

coevolutionary fuzzy modelling there are only two

species – one related to fuzzy variables and one

related to fuzzy rules, in the coevolution of two

groups of species one of groups contains species

related to fuzzy variables while the other one contain

species related to fuzzy rules.

Except the analogy, the rest of behaviour is

different. Figure 2 shows how it works. At the start

OPTIMIZATION OF STRUCTURE OF FUZZY-NEURAL SYSTEMS USING COEVOLUTIONARY ALGORITHM

127

co-operators from all species are selected. Then, one

of two groups is randomly selected. All members,

from all of the species of the selected group, are

simultaneously mutated. Then members from all of

the species (mutated and non mutated) are integrated

to create fuzzy-neural system (FNS on figure 2).

This fuzzy-neural system (as neural network) is

shortly trained via the specific backpropagation to

increase the quality of the model and to measure its

performance with the training dataset. After that

Matlab fuzzy inference system (FIS on figure 2)

object (MathWorks, 2009) is created from the fuzzy-

neural system. That FIS object is then validated with

the validation dataset. Based on the results of the

short training and the validation, fitness calculation

is performed. At the end fitness is assigned to each

of the mutated members and new, mutated members

are placed in the population. If the fitness of the

newly created fuzzy-neural system is the best one,

then it is recorded as the best known.

Coevolution of species and coevolution of two

groups of species are combined in the way that the

coevolution of species is a basic mechanism and the

coevolution of two groups of species is an additional

mechanism that helps escaping from local

optimums.

Fitness calculation is performed in three levels.

Each of levels has its purpose and influence on the

optimization process. Levels are following:

 The first level controls the overfitting. It holds

percentage results of training and validation near to

each other. That means that training progress is not

allowed if it is not followed by validation progress.

 The second level is used to maximize the total

accuracy. It is a sum of the accuracy of the training

and the accuracy of the validation.

 Third level is used to minimize the total number of

fuzzy rules in the model and to minimize the

absolute average error.

Levels have importance, which means that the first

level is more important than the second, and the

second is more important than the third.

2.3 Tests

Implementation of this hybridization is done in

MATLAB. Tests were performed with databases

from UCI Machine Learning Repository

(http://archive.ics.uci.edu/ml). Irvine, CA:

University of California, School of Information and

Computer Science). In this paper are presented some

results of tests with Iris database. Table 1 shows one

of tests that were composed of ten (10) runs with sa-

Figure 2: Coevolution of two groups of species.

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

128

Table 1: Results of one of tests with Iris database.

Run

Training+validation

result

Testing result Overall result

Number of

fuzzy rules

Comment

1. 128/130=98.46% 19/20=95.00% 147/150=98.00% 3

2. 125/130=96.15% 20/20=100.00% 145/150=96.67% 4

3. 122/130=93.85% 19/20=95.00% 141/150=94.00% 2

4. 128/130=98.46% 20/20=100.00% 148/150=98.67% 3

the best result

5. 126/130=96.92% 19/20=95.00% 145/150=96.67% 2

6. 130/130=100.00% 18/20=90.00% 148/150=98.67% 3

7. 126/130=96.92% 18/20=90.00% 144/150=96.00% 2

8. 121/130=93.08% 15/20=75.00% 136/150=90.67% 2 the worse result

9. 126/130=96.92% 20/20=100.00% 146/150=97.33% 4

10. 126/130=96.92% 18/20=90.00% 144/150=96.00% 2

Average 96.77% 93.00% 96.27% 2.7

same parameters. Since the Iris database is small, it

was split on training, validation and testing subsets

with ratios 11:2:2, respectively. Population size for

each of species was 50. Number of generations is

used as termination criteria and it was set to 1000

generations of the coevolution. This way all runs are

done under the same experimental conditions.

From the results in Table 1, and based on

characteristics of the hybridisation used in tests, and

parameters settings for this test, it is possible to note

the following:

 Obtained results in each run shows capability for

high classification of the generated fuzzy-neural

system. Having in mind that the number of

generations is limited, that only triangular

membership functions are used (less precise) and

that the fuzzy system is of Mamdani type (less

precise) then the classification result is high.

 Results were obtained in 1000 generations which

is near to similar usages of the coevolutionary

algorithm (Pena-Reyes, 2002) but without setting

any predefined element of the structure of the fuzzy-

neural system at the beginning. This shows the

strength of the presented approach in species

creation and automatic building of the system from

data.

 The fuzzy-neural system is build easily by setting

few parameters of the execution and providing the

dataset, without providing the initial structure of the

fuzzy-neural system. All is build from data

automatically. From the optimization point of view

this is harder problem than to optimize the structure

of the system that have some predefined elements.

 The overfitting is held well under control in most

of the runs, which is not easy with the small

database. This shows a good generalization

capability. The overfitting control results are a very

important fact for deciding which is the best build

system.

3 CONCLUSIONS

The hybridization of fuzzy logic, neural network and

coevolutionary algorithm is a very efficient

approach for the automatic generating the fuzzy-

neural system from data, whose main strength is in

usage of the cooperative coevolution in the way

presented earlier in this paper.

Cooperative coevolution implemented in this

way is a very good global search mechanism. When

more the two species are used in the coevolution

then mutation in one of the species makes a small

change and escaping from local optimums is not

fast, but with the coevolution of two groups of

species escaping from local optimums is faster

because several species simultaneously have a

mutation.

4 FURTHER WORK

Our special interests are hybridisations of soft

computing techniques, especially hybridisations that

include the cooperative coevolution. We will

continue to improve this hybridization of fuzzy

logic, neural network and coevolutionary algorithm,

and try to make some practical real-life applications

and build some systems in medicine and

bioinformatics. Coevolution of more than two

species is very interesting for parallel or distributed

implementation and that is also one of directions of

our interest.

OPTIMIZATION OF STRUCTURE OF FUZZY-NEURAL SYSTEMS USING COEVOLUTIONARY ALGORITHM

129

REFERENCES

Omanovic, S., Avdagic Z., 2011. Modeling of Fuzzy-

Neural Systems Using the Coevolutionary Algorithm.

In WSEAS’11, 12th International Conference on Fuzzy

Systems. WSEAS Press.

Pena-Reyes, C., 2002. Coevolutionary Fuzzy Modeling –

doctoral thesis, EPFL. Lausanne.

Nedjah, N., et al. (Eds.), 2005. Fuzzy System Engineering:

Theory and Practice, Chapter 3 - Adaptation of Fuzzy

Inference System Using Neural Learning (A.

Abraham), pp. 53-83, Springer. Verlag.

Kasabov, N., 2003. Evolving Connectionist Systems -

methods and applications in bioinformatics, brain

study and intelligent machines, Springer. Verlag.

Cordón, O., et al., 2001. Genetic Fuzzy Systems –

Evolutionary Tuning and Learning of Fuzzy

Knowledge Bases, World Scientific Publishing Co.

Pte. Ltd. Singapore.

Chen, Y., Abraham, A., 2010. Tree-Structure Based

Hybrid Computational Intelligence, Springer. Verlag.

Sivanandam, S. N., Sumathi, S., Deepa, S. N., 2007.

Introduction to Fuzzy Logic using MATLAB,

Springer. Verlag.

MathWorks, Inc., 2009. MATLAB Help.

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

130