CRITICAL BOUNDARY VECTOR CONCEPT IN NEAREST
NEIGHBOR CLASSIFIERS USING K-MEANS CENTERS
FOR EFFICIENT TEMPLATE REDUCTION
Wenjun Xia and Tadashi Shibata
Department of Electrical Engineering and Information Systems, The University of Tokyo
7-3-1 Hongo, Bunkyo-ku, 113-8656, Tokyo, Japan
Keywords: Nearest neighbor, Template reduction, k-Means clustering, Hardware implementation.
Abstract: Dealing with large data sets, the computational cost and resource demands using the nearest neighbor (NN)
classifier can be prohibitive. Aiming at efficient template condensation, this paper proposes a template re-
duction algorithm for NN classifier by introducing the concept of critical boundary vectors in conjunction
with K-means centers. Initially K-means centers are used as substitution for the entire template set. Then, in
order to enhance the classification performance, critical boundary vectors are selected according to a newly
proposed training algorithm which completes with only single iteration. COIL-20 and COIL-100 databases
were utilized for evaluating the performance of image categorization in which the bio-inspired directional-
edge-based image feature representation (Suzuki and Shibata. 2004) was employed. UCI iris and UCI Land-
sat databases were also utilized to evaluate the system for other classification tasks using numerical-valued
vectors. Experimental results show that by using the reduced template sets, the proposed algorithm shows a
superior performance to NN classifier using all samples, and comparable to Support Vector Machines using
Gaussian kernel which are computationally more expensive.
1 INTRODUCTION
The nearest neighbor (NN) classifier is one of the
most widely used nonparametric methods for pattern
recognition because of its simplicity for implementa-
tion. However, a number of implementations of the
algorithm suffer from its intrinsic burdens of repeti-
tive distance calculation with a large number of
template vectors, which lead to large memory occu-
pation and high computational cost.
To solve the problem, reducing the number of
samples is eagerly demanded. So far, many template
reduction techniques have been developed and dis-
cussed, but there still exist lots of issues. For exam-
ple, a supervised clustering is employed for editing
dataset in (Eick et al., 2004). Although the reduction
rates were quite high in their experiments, the accu-
racy was sometimes degraded after reduction, and
the clustering in the training session is extremely
complex and time-consuming due to the greedy
calculation. In (Zhou et al., 2009), by introducing a
sample austerity technique in conjunction with K-
means clustering, a better performance on both accu-
racy and reduction was achieved. However, the
process relies heavily on parameters, and its appli-
cability to tasks other than text categorization is
questionable because of the devolvement of bound-
ary information. Meanwhile, the template reduction
of kNN classifier proposed in (Fayed and Atiya.
2009) applies a chain finding method for selecting
boundary samples. Although achieving a good per-
formance, the method is still highly parameter de-
pendant, and not easy to implement. Among these
techniques, K-means clustering or similar center-
based scheme is being frequently employed in tem-
plate condensing of NN classifier (Wu et al., 2004);
(Eick et al., 2004) and (Zhou et al., 2009), but the
performance is still trapped by the complexity of
implementation and the difficulty of parameter de-
signing. To develop a method with efficient template
reduction rate while maintaining a high accuracy
performance, a more effective and less parameter
dependant method needs be developped.
In contrast, support vector machines (SVMs)
proposed in 1990s offer an efficient way to deal with
the problem of template reduction. By using only
93
Xia W. and Shibata T..
CRITICAL BOUNDARY VECTOR CONCEPT IN NEAREST NEIGHBOR CLASSIFIERS USING K-MEANS CENTERS FOR EFFICIENT TEMPLATE
REDUCTION.
DOI: 10.5220/0003642600930098
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 93-98
ISBN: 978-989-8425-84-3
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

critical boundary support vectors for classification,
SVM shows quite good performance in pattern rec-
ognition tasks (Chapelle et al., 1999) and (Bovolo et
al., 2010) as well as other applications. However,
SVM presents some serious shortcomings. Firstly,
unlike NN classifier, SVM is designed for binary
classification, which means complicated extra pro-
cedures are required for multi-class tasks (Hsu and
Lin, 2002). Moreover, the training process of SVM
is extremely time-consuming, usually ending up
with a massive amount of iterations to achieve con-
vergence. In addition, to get a good performance,
SVM often needs to employ kernel operations, for
example Gaussian kernel (Radial Basis Function
kernel), which is far more resource consuming than
simple distance calculation in NN. As a result, al-
though SVM is being widely used in software appli-
cations, there are not many examples of VLSI im-
plementation of Gaussian kernel-SVMs having on-
chip training functions. Therefore, since employing
boundary vectors for classification is a promising
way for efficient template reduction (Nikolaidis et
al., 2011), it is important to explore much simpler
methods for boundary vector selection as compared
to SVMs.
The purpose of this paper is to develop an effi-
cient template reduction method for the nearest
neighbor classifier using K-means centers, by intro-
ducing the concept of critical boundary vectors.
Different from the complex SVM training, the pro-
posed method is based on simple distance calcula-
tion which is more VLSI-hardware-implementation
friendly. In addition, it is easily extendible to multi-
class large-scale classification. To initially condense
the sample set, only K-means centers are utilized as
rough templates for classification, instead of using
the entire sample set. Then, in order to enhance the
classification performance, boundary vectors that are
critical for better accuracy are selected according to
a newly proposed training algorithm. In contrast to
the complex SVM training or other condensing
methods, only single iteration step is sufficient for
selection. Experimental results show that the pro-
posed algorithm has a superior performance to regu-
lar NNs and linear-kernel-SVM, and is comparable
to computationally expensive Gaussian kernel-SVM.
The organization of this paper is as follows. Sec-
tion 2 explains the proposed classification algorithm.
Section 3 reports the experiments conducted to
evaluate the performance of the proposed algorithm.
In addition, discussion on hardware implementa-
tion issues is given in Section 4. Finally, Section 5
gives a conclusion of this paper.
Figure 1: (a) original template vectors for 3-class classifi-
cation; (b) rough boundary determined by gravity centers
obtained using K-means clustering; (c) training process to
select critical boundary vectors to which weight=1 is
assigned (0 is assigned to others vectors); (d) classification
of a new input vector by finding the nearest vector from
boundary vectors and K-means centers.
2 ALGORITHM
The NN-based classifier developed in the present
work is explained in the following. It consists of two
stages: the training stage and the classification stage.
The final goal is to determine the decision bounda-
ries that assign a proper class label to a new input
vector using only a limited number of original tem-
plate vectors.
For a supervised classification task, a template
set  including samples belonging to  classes,
=
{


,⋯,

}
is given. Figure 1 illustrates a sim-
ple 3-class example of 2-dimension–vector classifi-
cation. Each class 

is defined as 

=


(

)
:=1,⋯,

, where 

(

)
is the i-th vector of
class-j, and 

is the total number of samples in the
j-th class.
Throughout the entire classification processing,
including K-means clustering and nearest neighbor
search, Manhattan distance function 

,

 is
used as dissimilarity measure because of its simplic-
ity in hardware implementation.


,

=

−

.
(1)
NCTA 2011 - International Conference on Neural Computation Theory and Applications
94

2.1 Training Stage
For condensing template vectors, the training stage
can be divided into two parts: a rough clustering by
K-means and the selection of critical boundary vec-
tors.
2.1.1 Rough Clustering
As a pre-processing of training, aiming at determin-
ing rough classification boundaries, K-means algo-
rithm using Manhattan distance is employed to ob-
tain the gravity centers in each class. These K-means
centers serve as substitution to all sample vectors in
the class and represent the sample category as shown
in Fig. 1(b). For each class 

, K-means clustering is
carried out only for samples belonging to the class 

,
thus obtaining K gravity centers


={

()
,⋯

()
}
of class-j.
As a pre-processing part, only a rough K-means
clustering is sufficient, therefore the iteration steps
in this part can be set to a very limited number.
2.1.2 Selection of Critical Boundary Vectors
In order to determine more accurate class boundaries
between two neighbouring classes, critical boundary
vectors are selected using a margin parameter .
In this scheme, a binary weight 

(

)
∈
{
0,1
}
is
assigned for each vector 

(

)
as shown in Fig. 1(c).
For a vector 

(

)
, assignment of weight 

(

)
is de-
cided according to the comparison of its distances
with the nearest center of intra-class centers 

(

)
and
the nearest sample of inter-class samples . After
weight assignment for all samples is finished, those
vectors weighted as 1 will form the critical boundary
vector set 

and other vectors with weight 0 will be
discarded from the template set. The weight 

(

)
is
defined according to the following rule:


(

)
=

0, min
∉



(

)
,≥min
…


(

)
,

(

)
(1+)
1, min
∉



(

)
,<min
…


(

)
,

(

)
(1+)
(2)
Here margin parameter  is used to control the cov-
erage of boundary vector selection and guarantee the
accuracy of classification.
2.2 Classification Stage
After the training stage as described above, classifi-
cation is carried out for a new input vector  as
shown in Fig. 1(d). Current template set T consists
of critical boundary vector sets {


,⋯


} and K-
means center sets {


,⋯


}. The decision function
() to assign class label is then defined as:

(

)
=min
…
( min


(

)
∈

∪

,

(

)
)
(3)
It should be noted that only single iteration is
sufficient for selecting boundary vectors and that
high-speed classification is possible using
remarkably low number of critical boundary vectors
along with K-means centers. Furthermore, as
similarity evaluation, Manhattan distance calculation
is much simpler as compared with kernel calculation
such as Gaussian kernel in SVM, which makes the
proposed method more hardware-implementation-
friendly.
In the proposed algorithm, the number of K-
means centers  and the margin parameter  are the
two key parameters to be determined for maximizing
the performance and efficiency. The influence of
variation in  and  is quantitatively assessed in the
following section.
3 EXPERIMENTAL RESULTS
AND DISCUSSION
To prove the effectiveness of the proposed algorithm,
four popular datasets were used in the experiments:
COIL-20, COIL-100 datasets from Columbia Object
Image Library, and Iris, Landsat Satellite datasets
from UCI machine learning repository. These data-
sets are all being widely used for verification of
classifiers such as NN, SVM and Radial Basis Func-
tion (RBF) networks. In our experiments, COIL-20
and COIL-100 were pre-processed to 64-dimension
vectors by an existing bio-inspired edge-based fea-
ture extraction method called Projected-Principle-
Edge-Distribution (Suzuki, Shibata. 2004), while Iris
and Landsat datasets are directly provided as 4-
dimension and 36-dimension vectors, respectively.
In addition, we have applied 3-fold cross validation
to COIL-20 and COIL-100 datasets for comparison.
The specifications of the four datasets are shown in
Table 1. Large variations in the number of classes,
the number of dimensions and the scale of datasets
have been included within the experiment sets.
The proposed classifier was implemented by C
language and compiled by GNU C Compiler Gcc-
4.3.2. Meanwhile, NN, SVM with linear-kernel,
SVM with RBF-kernel were used for comparison,
and the one-against-one practice has been adopted
CRITICAL BOUNDARY VECTOR CONCEPT IN NEAREST NEIGHBOR CLASSIFIERS USING K-MEANS
CENTERS FOR EFFICIENT TEMPLATE REDUCTION
95

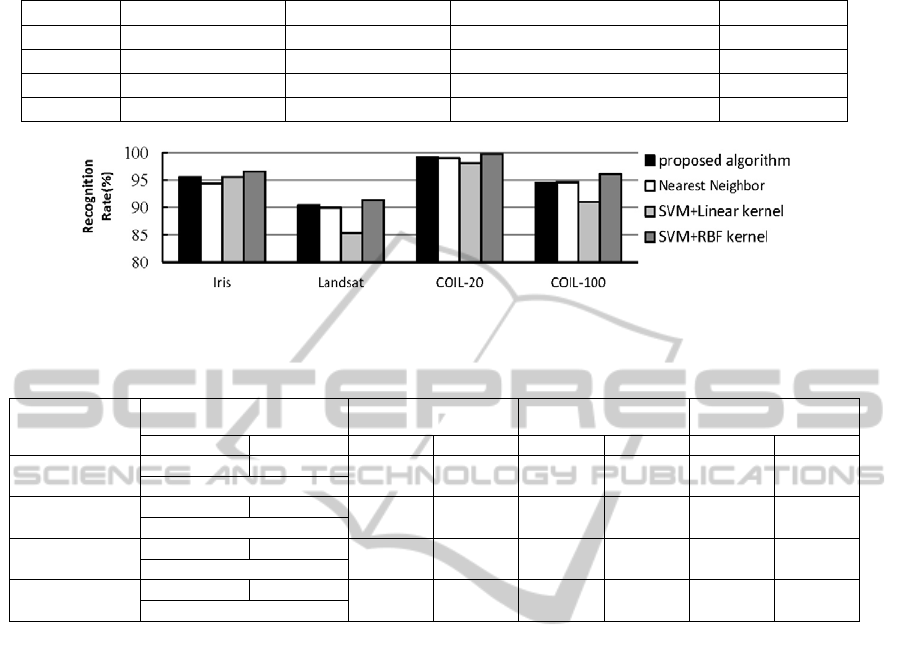
Table 1: Summary of data sets.
Dataset Number of categories Number of dimensions Number of training / testing samples Cross validation
UCI-Iris 3 4 60 / 90 No
UCI-Landsat 6 36 4435 / 2000 No
COIL-20 20 64 960/480 3-fold
COIL-100 100 64 4800/2400 3-fold
Figure 2: Comparison of accuracy performance.
Table 2: Summary of the recognition accuracy (Acc) and mean number of vectors in reduced template vectors (NRV) over
different datasets.
Dataset
proposed algorithm nearest neighbour
SVM
+ linear-kernel
SVM
+ RBF-kernel
Acc(%) NRV Acc(%) NRV Acc(%) NRV Acc(%) NRV
UCI-Iris
95.56 14
94.44 60 95.56 60
96.67 13
(K=1 α=0.25)
UCI-Landsat
90.45 2240
89.95 4435 85.25 1460
91.45 1640
(K=13 α=0.25)
COIL-20
99.24 351
99.03 960 98.19 632
99.79 702
(K=2 α=0.25)
COIL-100
94.58 2727
94.65 4800 91.06 4148
96.03 4220
(K=2 α=0.25)
for multi-class classification of SVM. The SVM
software used in these experiments was LibSVM.
3.1 Experimental Results
The results of classification accuracy are shown in
Figure 2. The average accuracy of proposed algo-
rithm is 94.96%, which is much higher than SVM
using linear-kernel, slightly higher than regular NN
classifier and comparable to SVM using RBF-kernel.
Detail data are shown in Table 2.
Figure 3 compares the number of reduced tem-
plate vectors for classification. Regarding the pro-
posed algorithm, the number equals to the summa-
tion of critical boundary vectors and K-means cen-
ters, and for SVM using RBF kernel, it means the
number of support vectors. The observation is very
interesting. For the two datasets with a small number
of classes (Iris and Landsat), the proposed algorithm
used nearly the same number of samples for classifi-
cation in Iris, and a little increased number of sam-
ples for classification in Landsat compared with
SVM. However, for other two datasets with rela-
tively larger class numbers, the proposed algorithm
has a superior performance in terms of template
reduction as compared to SVM.
It should be mentioned that for all datasets, the
value of  was set to 0.25. Actually within a series
of experiments, it has been empirically determined
that =0.25 yields the best value in terms of both
recognition accuracy and template reduction rate.
Therefore even if other values could show a slightly
better accuracy or improved reduction rate, the value
of 0.25 was used throughout the experiments for
comparison with other algorithms. Meanwhile, ex-
periments have also shown that the value of K does
not have a large impact on the performance. Further
discussion will be given in Section 3.3.
3.2 Benefit of Applying Critical
Boundary Vectors
To demonstrate the importance of using both critical
boundary vectors and K-means centers, three groups
of experiments R, R1 and R2, were carried out on
those large datasets according to the constitution of
template used for classification:
NCTA 2011 - International Conference on Neural Computation Theory and Applications
96

Figure 3: Comparison of the mean number of samples in reduced template sets used for classification. For NN, the value is
100% because all samples are used for classification. For SVM using RBF kernel, the value stands for the number of sup-
port vectors. For the proposed algorithm, it stands for the summation of K-means centers and critical boundary vectors.
Figure 4: Comparison of recognition accuracy using different part from reduced template set.
R: Use both critical boundary vectors and K-means centers as
template.
R1: Use only K-means centers as template.
R
2: Use only critical boundary vectors as template.
All the experiments were carried out by setting
the parameters same in Table 1, and the results are
shown in Figure 4. According to the results, we can
conclude that both critical boundary vectors and K-
means centers play important roles in classification.
However, there exist large variations among the
results of different datasets. This is because the
specifications including feature extraction methods,
category numbers of these datasets are totally differ-
ent. Therefore the distribution of their vectors in
feature space varies a lot. As a result, using either
part of the reduced template set in the proposed
algorithm can be hardly expected to show good
performance for all situations. In conclusion, intro-
ducing critical boundary vectors into the NN classi-
fier using K-means centers can not only improve the
accuracy performance, but also the robustness of
classifier dealing with various kinds of datasets.
3.3 Parameter Analysis
As mentioned earlier, margin parameter  and K-
means parameter
K are two parameters that related
to the performance in this algorithm.
According to the intrinsic characteristic of the
proposed algorithm, with the increasement of , the
number of selected critical boundary vectors
increases, which lead to higher computation cost and
resource consumption. On the other hand, accuracy
can be improved by increasing  to select more
critical boundary vectors. To explore the relationship
between  and performance, experiments about the
two parameters were carried out using two large
datasets Landsat and COIL-100. The curves of
classification performance versus  using different
K-means clustering parameter K are given in Figure
5. As shown in the figure, the accuracies become
saturated when the value of  reached about 0.25.
Even sometimes the saturation came below or above
the value, but the differences were very small.
Therefore, considering the performance on both
reduction rate and classification accuracy, the value
0.25 yields a better trade-off and was selected
emperically as the fixed value of .
Figure 5: Variation of accuracy rate by changing margin
parameter α and K, with comparison to NN.
CRITICAL BOUNDARY VECTOR CONCEPT IN NEAREST NEIGHBOR CLASSIFIERS USING K-MEANS
CENTERS FOR EFFICIENT TEMPLATE REDUCTION
97

At the same time, from Figure 5 we can conclude
that the value of K does not have a major influence
on the performance. Still it should be confirmed with
more examples. Currently it has been shown empiri-
cally that the value of K could be selected as about
4% of the minimum number of samples in single
class.
4 HARDWARE
IMPLEMENTATION ISSUES
As described in the algorithm part, the calculation of
the proposed algorithm is nearly the same with K-
means clustering. The dedicated custom VLSI chips
for large-scale K-means clustering have already
been developped (Shikano et al., 2007) and (Ma and
Shibata. 2010). By adding only a series of Margin
processing unit for calculating the multiplication of
 and distance, the algorithm can be easily
implementated on VLSI.
5 CONCLUSIONS
A template reduction algorithm for nearest neighbor
classifier using K-means centers based on critical
boundary vectors has been proposed. Experiments
have shown this algorithm has superior classification
performance to NN classifier and linear-kernel SVM,
while comparable to RBF-kernel SVM. The efficient
values of parameters have also been fixed empiri-
cally. In addition, this algorithm is highly computa-
tionally efficient and friendly to hardware imple-
mentation. Our further work will focus on the self
adaption of the K value.
REFERENCES
Bajramovic, F., Mattern, F., Butko, N., (2006). A com-
parison of nearest neighbor search algorithms for ge-
neric object recognition. In ACIVS’06, Advanced Con-
cepts for Intelligent Vision Systems.
Bovolo, F., Bruzzone, L., Carlin, L., (2010). A novel
technique for subpixel image classification based on
support vector machine. IEEE Transactions on Image
Processing, 19, 2983-2999.
Chapelle, O., Haffner, P., Vapnik, V. N., (1999). Support
vector machines for histogram-based image classifica-
tion. IEEE Transactions on Neural Networks, 10,
1055-1064.
Eick, C. F., Zeidat, N., Vilalta, R., (2004). Using represen-
tative-based clustering for nearest neighbor dataset ed-
iting. In ICDM’04, IEEE International Conference on
Data Mining.
Fayed, H., Atiya, A., (2009). A novel template reduction
approach for the k-nearest neighbor method. IEEE
Transactions on Neural Networks, 20, 890-896.
Hsu, C. W., Lin, C. J., (2002). A comparison of methods
for multiclass support vector machines. IEEE Transac-
tions on Neural Networks, 13, 415-425
Ma, Y., Shibata, T., (2010). A binary-tree hierarchical
multiple-chip architecture of real-time large-scale
learning processor systems. Japanese Journal of Ap-
plied Physics, 49, 04DE08-04DE08-8.
Nikolaidis, K., Goulermas, J. Y., Wu, Q. H., (2011). A
class boundary preserving algorithm for data conden-
sation. Pattern Recognition, 44, 704-715.
Shikano, H., Ito, K., Fujita, K., Shibata, T., (2007). A real-
time learning processor based on k-means algorithm
with automatic seeds generation. In Soc’07, the 2007
International Symposium on System-on-Chip.
Suzuki, Y., Shibata, T., (2004). Multiple-clue face detec-
tion algorithm using edge-based feature vectors. In
ICASSP’04, IEEE International Conference on Acous-
tic, Speech, and Signal Processing.
Wu, Y. Q., Ianakiev, K., Govindaraju, V., (2002). Im-
proved k-nearest neighbor classification. Pattern Rec-
ognition, 35, 2311-2318.
Zhou, Y., Li, Y. W., Xia, S. X., (2009). An improved
KNN text classification algorithm based on clustering.
Journal of Computers, 4, 230-237.
NCTA 2011 - International Conference on Neural Computation Theory and Applications
98