INVERSE METHOD FOR THE RETRIEVAL OF OCEAN

VERTICAL PROFILES USING SELF ORGANIZING

MAPS AND HIDDEN MARKOV MODELS

Application on Ocean Colour Satellite Image Inversion

Charantonis Anastase Alexandre

, Brajard Julien

, Moulin Cyril

, Bardan Fouad

and Thiria Sylvie

Laboratoire d’Océanographie Climat et Analyses Numériques, Université Pierre et Marrie Curie

Tour 45-55, 4, Place Jussieu, 75252, Paris, France

Laboratoire des Sciences du Climat et de l'Environnement, L'Orme des Merisiers, CEA Saclay

bat 712, 91191, Gif-sur-Yvette, France

Laboratoire CEDRIC, Conservatoir National des Arts et Metiers (CNAM), 292, Rue Saint Martin, 75003, Paris, France

Keywords: Self organising maps, Hidden markov models, Inversion, Geophysical, Chlorophyll-A, Satellite imaging,

Inversion.

Abstract: This paper presents a statistical inversion method used to infer 3D data from 2D imaging. The methodology

is based on a combination of the Self Organising Maps and the Hidden Markov Models. The method has

been validated by inferring the oceanic vertical profiles of Chlorophyll-A based on sea-surface data.

1 INTRODUCTION

The density of satellite observations allowed a semi-

continuous observation of the global ocean surface.

The two-dimensional images provided by this

coverage often contain information on integrated

quantities whose vertical distribution is unknown.

Depending on the field of study there exist different

dynamic approaches for inverting this type of data.

However, these approaches are often faced with the

problem of non-linearity, and can also be hampered

by a lack of knowledge of the complete mechanisms

that govern the distributions.

The present paper deals with the inversion of

observed sea-surface satellite images, noted 





∈



1⋯



, for retrieving of the vertical distribution

of Chlorophyll-A, noted 





∈



1⋯



, using a

statistical, non-linear approach.

The methodology we have developed is a

mixture of the neuronal algorithms known as Self

Organizing Topological Maps (SOM) and the

Hidden Markov Models (HMM). The SOM are

unsupervised classification algorithms, that allow us

to cluster our availiable data into classes. The classes

are arranged on a topological map and connected to

each other by a topological similarity distance. In the

present study the SOM classification is applied

twice, once on the sea-surface data, and once upon

the vertical profiles connected to these images. The

resulting topological maps allow us to discretize

both data spaces into set amounts of classes.

The second statistical algorithm, the HMM

allows us to infer the most likely sequence of some

discrete, unobservable states, given a series of

discrete, observable states. To do so a set of

probability matrices are calculated, corresponding to

the dynamic processes of the unobserved states and

the links existing between the observed and

unobserved states. We use the classes created

through the SOMs to discretize the availiable data

and therefore represent both the observable and the

unobservable states.

In this paper, we present the results obtained

with the methodology developed on a case study at

the site of the Bermuda Atlantic Time Series

(BATS) (32 N -64 W) of the JGOFS campaign.

2 SELF-ORGANIZING

TOPOLOGICAL MAPS

Self-Organising Topological Maps (SOM) are

316

Anastase Alexandre C., Julien B., Cyril M., Fouad B. and Sylvie T..

INVERSE METHOD FOR THE RETRIEVAL OF OCEAN VERTICAL PROFILES USING SELF ORGANIZING MAPS AND HIDDEN MARKOV MODELS

- Application on Ocean Colour Satellite Image Inversion.

DOI: 10.5220/0003644703160321

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 316-321

ISBN: 978-989-8425-84-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

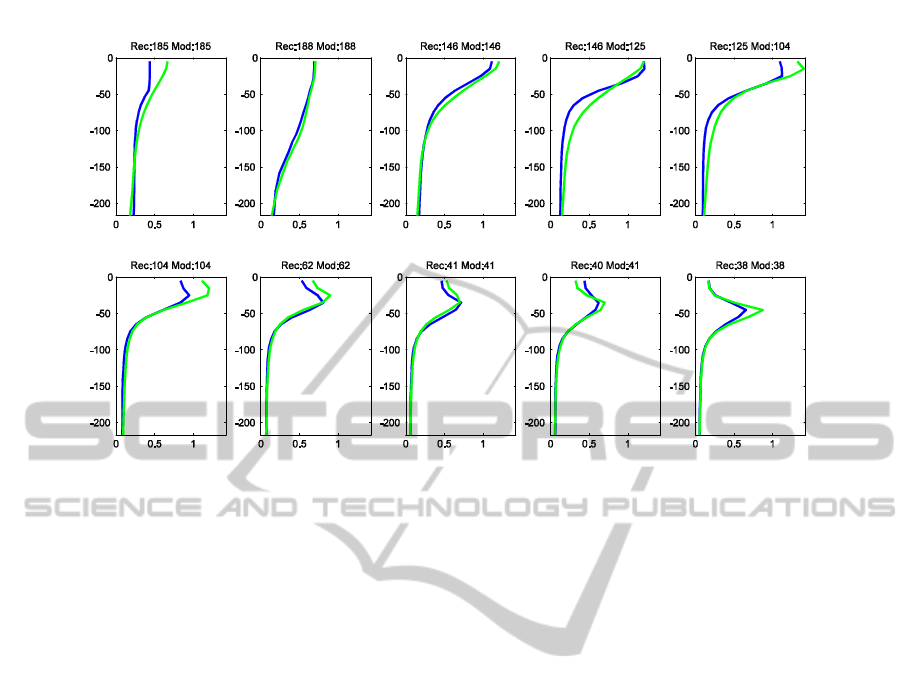
Figure 1: Inversion of ten 5-days steps for the period from 04-04-2005 to 05-19-2005, at BATS. In green, the states

provided by the inverse method and in blue the vertical distribution of Chlorophyll-A according to the NEMO-PISCES

model. The horizontal axes are in 10

μmol/L of Chlorophyll-A, while the vertical ones are in meters from the sea surface.

The numbers on top correspond, after Rec, to the indexes of the classes on M

dis

attributed to that 5-day step by the inverse

method, and, after Mo to the indexes attributed by projection of the total profile on M

dis

. These are not show in the figure.

clustering methods based on neural networks (S,

Haykin 1999). They provide a discretization of a

learning dataset A= {



∈



, k =1...N } into a

reduced number of subsets, called classes, P

, { i =

1...M } that share some common statistical

characteristics. Each subset is represented by its

referent vector r

which approaches the mean value

of the elements in the class Pi. In our case, we

trained two SOMs, one containing the observations,

called M

obs

and one containing the distributions of

the unobservable states, called M

dis

. The number of

classes in M

obs

and M

dis

are respectively noted N

obs

and N

dis

The topological aspect of the maps can be

justified if we consider the Map as an undirected

graph on a two-dimensional lattice whose vertices

are the m classes. This graph structure therefore

allows the definition of an discrete distance d(i,j)

between two classes i and j, defined as the length of

the shortest path between i and j on the map. The

nature of the SOM training algorithm forces a

topological ordering upon the map, and therefore

any neighbouring classes c

and c

on the map have

referent vectors r

and r

that are close in the

Euclidian sense in the data space R

.The topological

ordering constitutes a major element of our inverse

method, since it allows us to make, latter on, the

ergodic assumption for our Markov states.

We define a series of observable events by taking

the data from observations related to a given period

of time and we label each observation by the index

of the class to which it is assigned by using M

obs

This classification is done by allocating to each

observation 





∈



1⋯



, in the sequence the

index of the class of M

obs

whose referent is the

closest to it in the Euclidian sense. Therefore we

obtain the series

obs

= 





=











−





,

=1⋯





(1)

In the same way, we obtain the time-series of

distributions

dis

= 





=











−





, =

1⋯





(2)

These series S

obs

and S

dis

are used by the HMM in

order to estimate the probabilistic links that exist

between the observable states and the unobservable

ones.

The referents r

dis

of M

dis

are also used as the

vertical profiles in our sequence reconstructions.

04-04-2005 09-04-2005 14-04-2005 19-04-2005 24-04-2005

29-04-2005 04-05-2005 09-05-2005 14-05-2005 19-05-2005

INVERSE METHOD FOR THE RETRIEVAL OF OCEAN VERTICAL PROFILES USING SELF ORGANIZING MAPS

AND HIDDEN MARKOV MODELS - Application on Ocean Colour Satellite Image Inversion

317

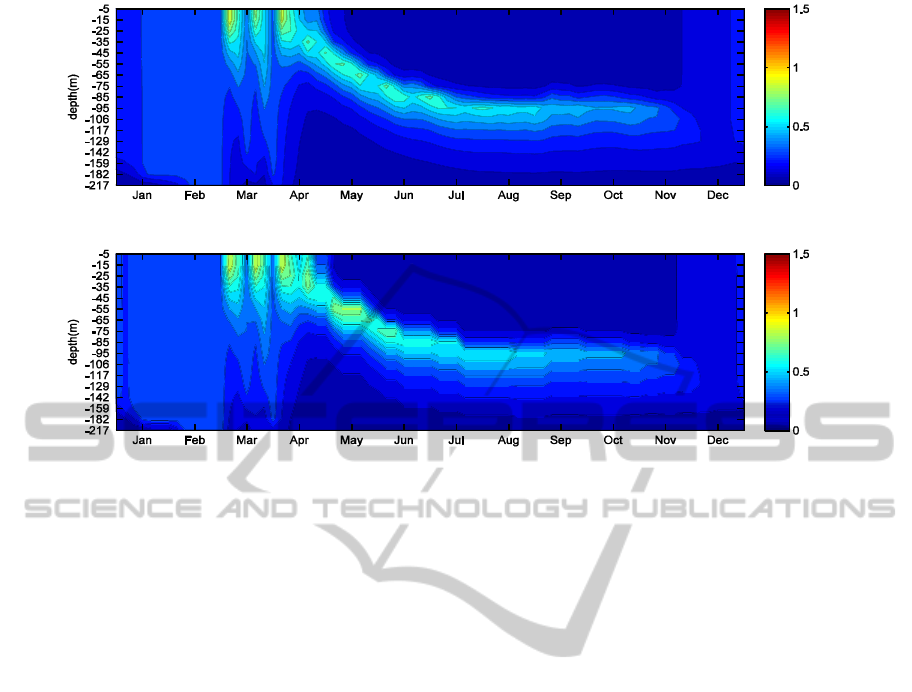
Figure 2: The reconstruction at BATS of the validation year 2005, according to, the NEMO-PISCES MODEL (top graph)

and the inverse method result (bottom graph). The colorbar indicates the Chlorophyll-A concentration in 10

μmol/L.

3 HIDDEN MARKOV MODELS

A Markov model is a stochastic model that assumes

the first order Markovian property, meaning that

each consecutive state of the model depends solely

on its previous stat of the model such as

P(X

| X

... X

t-1

) = P(X

| X

t-1

) (3)

Expanding this principle, a Hidden Markov Model

(HMM) is a stochastic model with two sequences.

One sequence of unobservable states that follow the

first order Markovian property, (represented in our

method by S

dis

), and one sequence of observable

states, (represented by S

obs

), that have a statistical

link with the unobservable states (O. Cappé et al.,

2005).

We consider two phases, a training one, and a

retrieval one. During the training, the Transitions

matrix Tr and the Emissions matrix Em are

estimated. Tr contains the transition probabilities of

the unobserved states

i,j

= P(C

dis(i,t)

| C

dis(j,t-1)

) (4)

where

∑



,









(5)

Tr corresponds, in a physical sense, to the

underlying dynamics that govern the unobserved

states.

Em contains the à posteriori probabilities of

each observed state to have been emitted by an

unobserved state,

i,j

= P(C

dis(i,t)

| C

obs(j,t)

)

(6)

where

∑



,









(7)

Em corresponds, in a physical sense, to the link

existing between the observed quantities and the

dynamics of the unobserved quantities. Another

probability matrix that needs to be calculated is the

initial probability matrix Π, with components π

which represent the average revisit rate of each

unobserved state given an infinite sequence. All

mentioned probabilities are estimated by using the

Baum-Weltch algorithm (L. E. Baum et al., 1970),

which is a maximum likelihood optimization

algorithm, that takes as input the sequences S

obs

and

dis

and outputs the most likely matrices to have

generated them through a hidden Markov process.

During the recognition phase, we used the

Viterbi algorithm, which is a well-know dynamic

programming algorithm (Viterbi AJ, 1967), for

inferring the most likely sequence of indexes S

dis-est

representing the unobserved states, given the

previously estimated parameters Tr, Em and Π of the

HMM and a sequence of observations S

obs-new

. It is

well documented (M.S. Ryan and G.R. Nudd. 1993)

that the Viterbi algorithm can face problems due to

NCTA 2011 - International Conference on Neural Computation Theory and Applications

318

Figure 3: The top image contains the absolute error between the NEMO-PISCES model and the result of the inverse

method, at BATS for the validation year 2005. The bottom image contains the absolute relative error between the NEMO-

PISCES model and the result of the inverse method.

transitions that were not observed in the training

data set. A balance needs to be found between the

sizes of the SOM maps that will determine the

amount of discretization provided by the method,

and the correctness of the allocation of indices. The

dimensions of each map are therefore optimized

using a validation set. Yet, even with an

optimization there will be some situations and

transitions that are seldomly encountered in the

training data and result in null probabilities in the

probability matrices Em

B-W

and Tr

B-W

that we

estimated in the first pass of the Baum-Weltch

algorithm.

Due to this usual lack of sufficient data in the

concerned domains, Em

B-W

and Tr

B-W

need to be

adjusted. This is done by taking into account the

properties of the topological maps. A major

characteristic of the present method is to use the

topological order in order to improve the accuracy of

the estimated probabilities matrices. The topological

maps allow us to modify the probabilities by

allowing each state to communicate via a diminutive

probability with each of its neighbouring states.

This is done by considering the neighbourhood

matrices NM

obs

and NM

dis

, of dimensions (N

obs

)

and (N

dis

), where

SOM

(i,j)=

1,i

d





,





<2

0,

(8)

with d(i,j) being the discrete distance of the map.

Taking into account the neighbourhood consists in

increasing the probability of reaching a class j from

a class i, by an ammount proportional to the sum of

the previously calculated probabilities of reaching

the neighbour classes of class j on SOM. In order to

favour the data observed during training, we add a

weighting term, noted w

, to the initial probabilities,

and we further multiply it by the total length of the

training sequences used in the intitial Baum-Weltch

algorithm’s pass, noted T

training

, since this length is a

measure of confidence in the correctness of the

estimated parameters. The matrices obtained are

then normalized. The final Em and Tr matrices we

use, noted Em

final

and Tr

final

, are computed by

applying:







,





=



∗



∗







,





∑







,



∗











,





(9)

Which is normalized to fit the constraint (7), and







,





=



∗



∗







,





∑







,



∗











,





(10)

Which is normalized to fit the constraint (5). For this

application w

is set to 9.

INVERSE METHOD FOR THE RETRIEVAL OF OCEAN VERTICAL PROFILES USING SELF ORGANIZING MAPS

AND HIDDEN MARKOV MODELS - Application on Ocean Colour Satellite Image Inversion

319

These modifications permit the Viterbi algorithm

to circumvent the problems of impossible

transitions, or emissions due to insufficient data in

the training sequences that resulted in nul

probabilities in the estimated parameters.

4 APPLICATION FOR THE

RESTITUTION OF THE

VERTICAL CHLOROPHYLL-

A CONCENTRATION

THROUGH SEA SURFACE

DATA

The bio-geochemical activity of the oceans and the

carbon cycle are two parts of a complex feedback

system. A change in climate and an increase of the

amount of available carbon can affect the primary

oceanic production, and in return a change in the

bio-geochemical activity affects, by modifying the

albedo and carbon fixation rates, the climate and

carbon concentration. It is therefore important to be

able to determine the oceanic primary production. In

recent years, many algorithms have been developed

that infer the Chlorophyll-A concentration in ocean

surface layers through satellite imaging (Brajard et

al., 2008). It has also been proved that the vertical

Chlorophyll-A distribution, is correlated with sea

surface data (Uitz et al., 2006). Therefore, the

determination of the vertical distribution of

Chlorophyll-A from sea surface data is a problem

that can be solved by the methodology we propose.

One cannot determine the vertical distribution of

Chlorophyll-A without first understanding the

parameters that influence the development of

phytoplankton. It is generally accepted that

phytoplankton growth depends on 5 parameters:

available radiation, available nutriments, predators

and biology, water temperature, water turbidity.

These parameters cannot easily be monitored

through a direct approach. Satellite imaging,

however, can give us proxy information, which can

be used in an empirical approach for determining the

vertical distribution of Chlorophyll-A. Specifically,

in this study we used: Sea Surface Chlorophyll-A

concentration (SCHL), Sea Surface Temperature

(SST), Sea Surface Elevation (SSH), Shortwave

Radiation (SR) and Wind-speed Intensity (WS).

Since our objective is to validate the theoretical

methodology, we used simulated data in order to test

the validity of our approach. We therefore

approximated the satellite values of the previous

parameters by using the input and output values

provided by the NEMO oceanic circulation model

coupled to the PISCES bio-geochemical model (C.

Moulin, 2008). In order to better simulate the noise

and errors inherent to satellite images we added a

white noise z ~ N(0,ê), ê=1/2 * (σ

schl

, σ

sst

, σ

ssh

, σ

) to the parameters that could be gathered from

satellite imaging. σ represents the standard

derivation of each corresponding surface parameter,

as computed on the training data. The application

was set at the site of BATS.

The unobserved states that were classified, were

the output data vectors containing the average

vertical Chlorophyll-A distribution at 17 depth

levels (from 5 meters to 217) and temperature

distribution at 9 depth levels. These vertical

distribution profiles were 5-day averages spanning

the period from 1991 to 2007 located in a 2°x2°

square centred on BATS. Therefore M

dis

belongs to

(17 levels of Chlorophyll-A + 9 levels of

Temperature). M

obs

belongs to R

We trained M

obs

and M

dis

by taking into account

all available profiles at BATS, as well as any

adjacent points included in the model. This gave us

9*73*17=11169 profiles for the construction of the

maps. The optimum map sizes, N

obs

and N

dis

were

determined to be 21*14=294 classes.

For the estimation of the HHM parameters on

the other hand, we take a total of 14 years (1991-

2004) for the training, each including seventy-three

5-day steps. Therefore T

training

=1022. We maintained

3 years (2005-2007), or 219 5-day steps, to validate

our approach.

The results shown in Figure 1 present the

temporary evolution of Chlorophyll-A profiles in ten

5-day steps sequence, from 04-04-2005 to 19-05-

2005, at BATS. In green we see the Chlorophyll-A

distribution profiles, taken from the referents r

dis

, corresponding to the indexes of the

reconstructed time series S

dis-rec

. In blue we can see

the vertical distribution of Chlorophyll-A according

to the NEMO-PISCES model at the same 5-day

steps.

In Figure 1 we also have, preceded by the

acronym Rec, the indexes that constitute time series

dis-rec

and, preceeded by Mod, the indexes we obtain

by projecting the corresponding profiles of the

NEMO-PISCES model on M

dis

. In order to avoid

confusion, the profiles corresponding to the indexes

after Mod are not displayed. When the vertical

distribution of Chlorophyll-A is know, these indexes

would correspond to the optimum reconstruction we

could get with M

dis

. We note this optimum time

series as S

dis-opt

. It is interesting to notice that even

NCTA 2011 - International Conference on Neural Computation Theory and Applications

320

when the indexes are not equal, the classes are

neighbours on M

dis

, and the estimated profiles are

quite similar to the observed ones.

If we define S

dis-2005to2007

as the reconstructed

time series of indexes of the validation years from

2005 to 2007 and as S

dis-opt-2005to2007

the

corresponding optimum reconstruction we observe

that they are in agreement 84,59% of the time. This

perforance reaches 88,58% when applied on the

reconstruction S

dis-2005

of the year 2005 alone, as

compared to its optimum reconstruction. This was

probably due to the validation year 2005 having a

small variation from the mean year, and presenting

often-observed transitions. In the training date we

had on average an agreement of 86,46%

In Figures 2 and 3, we applied the inverse

method to the full 73 5-day steps serie of the

validation year 2005. We can observe that the

reconstruction closely fits the results provided by the

NEMO-PISCES model. The correlation index of the

two images in Figure 2 is 97,30%.

We can notice that the discretization induced by

the SOM is apparent, yet the general form and

intensity are correctly represented, as it becomes

clear in Figure 3, where the error graphs tend to have

small values.

5 CONCLUSIONS

In the present paper we have introduced an inversion

method based on SOM and HMM, that is able to

reconstruct the vertical profiles of Chlorophyll-A

based on satellite images. One of its main

advantages in the inversion of Chlrophyll-A is that it

does not use Gaussian approxiamtions used in other

methods (Morel 1988, Uitz et al., 2006), allowing

the reconstruction of situations where the

distribution is not conforming to a single gaussian

curve. An additional benefit of the inversion method

presented, is its efficiency in terms of calculations.

The method is open ended enough to be applicable

for the inversion of the profiles of different bio-

geophysical parameters based on satellite imaging.

We plan to further validate this method by

testing its robustness with satellite imaging and in-

situ data, as well as to apply it on different types of

profiles, such as oceanic salinity or temperature

profiles. A latter goal is to expand the method to

take spatial constraints into consideration, and

reconstruct 3D profiles.

ACKNOWLEDGEMENTS

We would like to thank the “Délégation Generale de

l’Armement” for financing this work.

REFERENCES

S, Haykin 1999. "9. Self-organizing maps". Neural

networks - A comprehensive foundation (2nd ed.).

Prentice-Hall

L. E. Baum, T. Petrie, G. Soules, and N. Weiss, 1970. "A

maximization technique occurring in the statistical

analysis of probabilistic functions of Markov chains",

Ann. Math. Statist., vol. 41, no. 1, pp. 164–171.

F. Badran, M. Berrada, J. Brajarda M. Crépon,C. Sorror,

S. Thiria, J.-P. Hermand M. Meyer, L. Perichob and

M. Asch, 2008. "Inversion of satellite ocean colour

imagery and geoacoustic characterization of seabed

properties: Variational data inversion using a semi-

automatic adjoint approach", Journal of Marine

Systems, Volume 69, Issues 1-2, Pages 126-136

C. Moulin, A. Kremeur, A. El Moussaoui, C. Ethe, L.

Bopp, E. Dombrowsky, E. Greiner, O. Aumont, P.

Brasseur, 2008. "Understanding the interannual

variability of the oceanic carbon cycle: Results from

the coupled biogeochemical-physical global model

PISCES-NEMO", American Geophysical Union, Fall

Meeting 2008, abstract #OS31A-1226 Journal of

Marine Systems,Volume 69, Issues 1-2, Pages 126-136

J. Uitz, H. Claustre, A. Morel, S. B. Hooker, 2006

"Vertical distribution of phytoplankton communities in

open ocean: An assessment based on surface

chlorophyll", Journal of Geophysical Research

Vol.111.

Olivier Cappé, Eric Moulines, and Tobias Rydén, 2005.

"Inference in Hidden Markov Models." Springer.

Viterbi A J, 1967. "Error bounds for convolutional codes

and an asymptotically optimum decoding algorithm".

IEEE Transactions on Information Theory 13 (2):

260–269.

M. S. Ryan and G. R. Nudd. 1993. The Viterbi Algorithm.

Technical Report University of Warwick RR-238

INVERSE METHOD FOR THE RETRIEVAL OF OCEAN VERTICAL PROFILES USING SELF ORGANIZING MAPS

AND HIDDEN MARKOV MODELS - Application on Ocean Colour Satellite Image Inversion

321