CHAOTIC ANALYSIS OF METAL CUTTING WITH
NONLINEAR SUSPENSION
Cai-Wan Chang-Jian, Hsieh-Chung Hsu, Guan-I Wu and Cheng-I Weng
1
Department of Mechanical and Automation Engineering, I-Shou University, 1, Section 1, Hsueh-Cheng Rd.
Ta-Hsu Hsiang, Kaohsiung County, Taiwan 840, R.O.C.
Keywords: Chaos, Cutting, Nonlinear suspension.
Abstract: This study performs a systematic analysis of dynamic behavior of cutting process of machine tool with
unbalance force induced from mass eccentricity of work-piece, nonlinear cutting force and nonlinear
suspension effect. Phase diagrams, power spectra, bifurcation diagrams and Poincaré section are applied to
identify the dynamic motions in this study. The simulation results show that the non-periodic dynamic
responses are very abundant in cutting process of machine tool. The results presented in this study provide
an understanding of the operating conditions under which undesirable dynamic motion takes place in this
kind of system and therefore serve as a useful source of reference for engineers in designing and controlling
such systems.
1 INTRODUCTION
Since the mechanisms among tool, workpiece and
chip are complicated in the cutting process, the
analytical difficulties are increased in studying
related academic researches and the complete
studying is also hard to achieve. There are many
significant and dramatic investigations are
performed before. The dynamics analysis of cutting
based on the model of Hastings, Oxley and
Stevenson was the most popular model for many
studies and many studies are based on the
mathematical model proposed by them (Hastings et
al., 1971). Grabec presented a series of papers
discussing chaotic dynamic responses occurring in
cutting machines and also found some mechanisms
of chaos in the cutting process (Grabec, 1988).
Altintas, Eynian and Onozuka investigated the
influence of vibrations on the cutting forces (Altintas
et al., 2008). Powalka, Pajor and Berczynski
presented a special experiment used for cutting force
identification to eliminate the regenerative
phenomenon and also to improve the accuracy
(Powalka et al., 2009). Hamed, Firooz, Mohammad
and Mohammad proposed a single degree of
freedom dynamic system including quadratic and
cubic structural nonlinearities and found abundant
nonlinear behaviors (Hamed et al., 2010). Therefore,
we would know that cutting process is a highly
nonlinear phenomenon and the linearization or
simplification of analyzing cutting process may
cause some simulation errors.
The related literatures are very comprehensive,
some assumptions or linearization are performed in
order to simplify the simulation model and
economize simulation time. The assumptions or
linearization may lead some dramatic errors
comparing with real state. In this study, we consider
the nonlinear dynamic responses in cutting process
of machine tool with nonlinear suspension effect and
also take the nonlinear cutting force into
consideration. The nonlinear dynamic equations are
solved using the fourth order Runge-Kutta method.
The dynamic trajectories, power spectrum, Poincaré
maps and bifurcation diagrams are applied to
analyze dynamic motions.
2 MATHEMATICAL MODELING
Fig. 1 represents the model of metal cutting under
nonlinear suspension. K
1x
and K
2x
are the first and
second equivalent stiffness coefficients in the
vertical direction; K
1y
and K
2y
are the first and
second equivalent stiffness coefficients in the
horizontal direction; C
x
and C
y
are the damping
501
Chang-Jian C., Hsu H., Wu G. and Weng C..
CHAOTIC ANALYSIS OF METAL CUTTING WITH NONLINEAR SUSPENSION.
DOI: 10.5220/0003645305010504
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (MSIE-2011), pages 501-504
ISBN: 978-989-8425-75-1
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

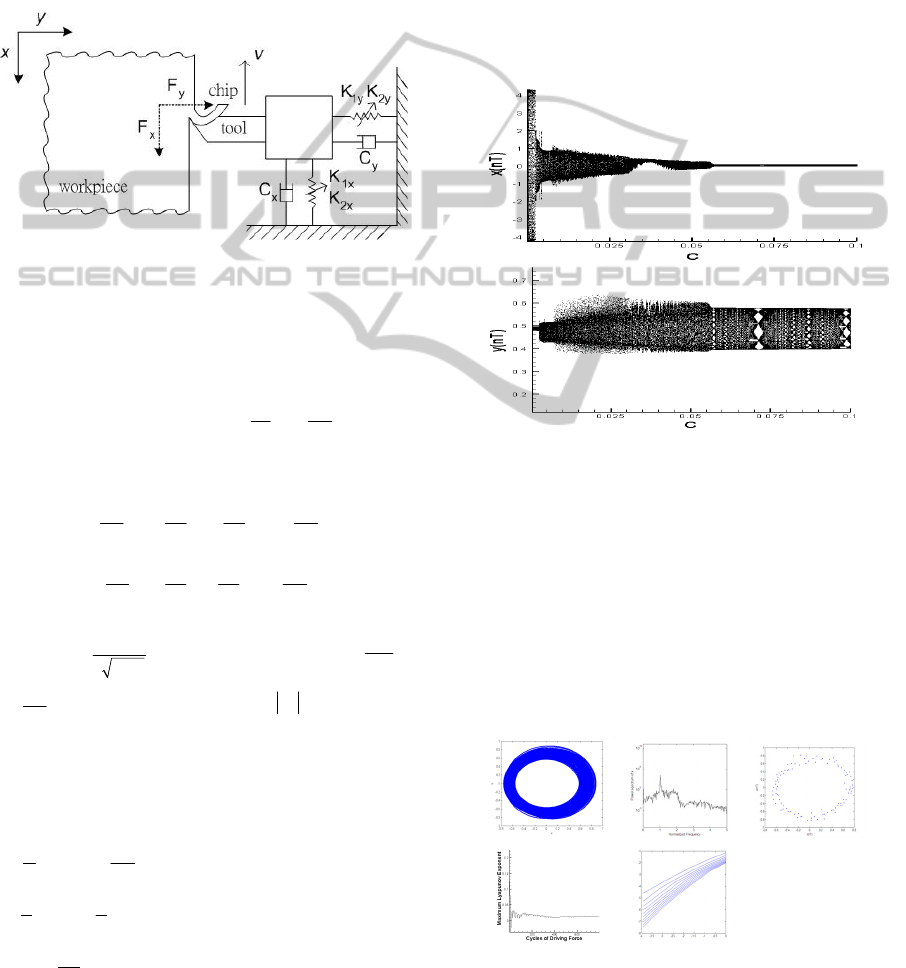
coefficients of the supported structure in the vertical
and horizontal directions respectively; F
x
and F
y
are
the components of external excited cutting forces; F
y
is the cutting force dependence on the cutting speed
and chip thickness; F
x
is the thrust force which is
related to the main cutting force through a related
frictional coefficient μ (F
x
=μF
y
). The nonlinear parts
of dynamic equations include nonlinear suspension
term (hard spring case) and the nonlinear cutting and
thrust force term.
Figure 1: Model of metal cutting under nonlinear
suspension.
3
12
x
M
xCxKxKx F++ + =
 
(1)
3
12 y
M
yCyKyKy F++ + =
 
(2)
Let X= x
/h
0
; Y= y/h
0
; τ = ω t;
dd
dt d
ω
τ
= ; （
•
）
denotes d/dt and（′）denotes d/dτ.
3
22
21
x
F
XXXX
s
p
ss
ξα
′′ ′
+++ =
(3)
3
22
21
y
F
YYYY
s
p
ss
ξα
′′ ′
+++ =
(4)
where
1
2
C
K
M
ξ =
,
2
0
pMh
ω
=
,
2
2
2
n
s
ω
ω
=
,
2
2
0
1
K
h
K
α =
,
yx
F
F
μ
=
,
2
01
[( 1) 1]()
xr
FqhCV Hh=−+
,
22
23
[ ( 1) 1][ ( 1) 1] ( ) sgn( )
f
xf
Cv Ch HF V μ =−+−+
[2-3],
0r
VVX
′
=−
,
0f
VVRY
′
=−
,
0
hh Y=−
, and
2
04
[ ( 1) 1]
r
RRCV=−+
.
()
x
H
F
may be approximated
as
1
[1 tanh( )]
2
x
F
ε
+ , ()
H
h may be approximated
as
1
[1 tanh( )]
2
h
ε
+
and
sgn( )
f
V
may be approximated
as
tanh( )
f
v
ε
.
The fourth order Runge-Kutta method is applied
to carry out the numerical analysis. These numerical
data are then used to generate the dynamic
trajectories, power spectrum, Poincaré maps and
bifurcation diagrams.
3 NUMERICAL RESULTS AND
DISCUSSIONS
In the present study, the nonlinear dynamics of the
cutting system shown in Figure 1 are analyzed using
Poincaré maps, bifurcation diagrams, the Lyapunov
exponent and the fractal dimension.
Figure 2: Bifurcation diagrams for geometric center of
cutting system using dimensionless damping ratio,
ξ
, as
bifurcation parameter.
The nonlinear dynamic equations presented in
Eqs. (3) to (4) for the cutting system with nonlinear
suspension effects and strongly nonlinear cutting
force were solved using the fourth order
Runge-Kutta method. The time step in the iterative
solution procedure was assigned a value of
π /300
and the termination criterion was specified as an
error tolerance of less than 0.0001.
Figure 3: Simulation results obtained for cutting system
with
ξ
=0.015 (x).
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
502

Figure 4: Simulation results obtained for cutting system
with
ξ
=0.015 (y).
Figure 5: Simulation results obtained for cutting system
with
ξ
=0.025 (x).
Figure 6: Simulation results obtained for cutting system
with
ξ
=0.025 (y).
In practical cutting systems, dimensionless damping
coefficient
ξ
is commonly used as a control
parameter. Accordingly, the dynamic behavior of the
current cutting system was examined using the
dimensionless damping coefficient
ξ
as a
bifurcation control parameter. Figure 2 presents the
bifurcation diagrams for the cutting system
displacement against the dimensionless damping
coefficient
ξ
. The bifurcation diagrams show that
the geometric center of cutting system performs
non-synchronous motions in horizontal and vertical
directions. The strongly non-periodic or even chaotic
motions occurring at lower dimensionless damping
coefficient and convergent its non-periodic dynamic
responses to be periodic motions and the vibration
amplitude also decreased at higher values in the
horizontal direction, i.e.
0.0575
ξ
>
. The above
simulation result is seemed to be satisfied natural
phenomenon. Though in the meantime, the dynamic
responses of the cutting system in the vertical
direction behave strongly different comparing with
horizontal cases. As damping coefficient increases,
the dynamic motions still perform non-periodic
response and even for higher values (
0.0575
ξ
> ).
Thus we found very interesting non-synchronous
motions in vertical and horizontal directions
especially at higher damping coefficients. As we
know, we may think the cutting system or other
vibrating machine system would become steady at
higher damping coefficient but actually the
suspension of this system is highly nonlinear
(Naturally or technically speaking, the suspension of
those machine systems should be nonlinear case).
Thus we may not seem they to be synchronous
behaviors in the vertical and horizontal directions of
the cutting systems and it may provide some
interesting or considerable information to analyze or
control these kind of systems. Figures 3 to 6 are the
phase diagrams, power spectra, Poincaré Map,
Lyapunov exponent and fractal dimension of the
cutting system found chaotic motions at
0.015 0.025and
ξ
=
in vertical and horizontal
directions. It also shows that the dynamic responses
are synchronous in vertical and horizontal directions
from observing simulation results, firstly. Secondly,
Phase diagrams show disordered dynamic behaviors;
power spectra reveal numerous excitation
frequencies; the return points in the Poincaré maps
form geometrically fractal structures; the maximum
Lyapunov exponent is positive; the fractal
dimensions are found to be non-integer. Thus we
may conclude that the dynamic motions perform
chaotic motions at the above control parameters with
the simulation results are corresponding with one
another. The dimensionless rotating speed s is also
an important control parameters to analyze dynamic
responses of rotating machines. Figure 7 present the
bifurcation diagrams for the dimensionless
displacement in the vertical and horizontal direction
of the cutting system using the dimensionless
rotating speed s as a bifurcation parameter. It can be
observed that the cutting system behaves periodic
motions at low rotating speeds and exhibits
CHAOTIC ANALYSIS OF METAL CUTTING WITH NONLINEAR SUSPENSION
503

non-periodic or even chaotic motions at high values
of the dimensionless rotating speed. Besides, we also
found that they are synchronous in the vertical and
horizontal directions.
Figure 7: Bifurcation diagrams for geometric center of
cutting system using dimensionless rotating speed, s, as
bifurcation parameter.
4 CONCLUSIONS
This work shows that chaotic behavior exists in the
cutting system with nonlinear suspension and
nonlinear cutting force. Some interesting and useful
simulation results are also found in this study.
Specially, we found that dynamic responses behave
non-synchronous in the vertical and horizontal
directions with the increasing of the value of
dimensionless damping coefficient. It is well known
that if a nonlinear dynamic system behavior is
chaotic, the resulting broad band vibration with
comparatively large vibrational amplitude will
enhance the probability of fatigue failure. In order to
increase the working life of cutting system or
enhance the performance of cutting system, it is
important not to operate the whole system at chaotic
motions. Therefore, this study may aid the
theoretical understanding of nonlinear systems of
cutting machine tool and escape the undesired
dynamic responses for machining.
REFERENCE
Altintas, Y., Eynian, M. and Onozuka, H. (2008).
Identification of dynamic cutting force coefficients
and chatter stability with process damping. Annals of
CIRP, 57, 371-374.
Grabec, I. (1988). Chaotic dynamics of the cutting process.
International Journal of Machine Tools and
Manufacture, 28, 19-32.
Grabec, I. (1988). Explanation of random vibrations in
cutting on grounds of deterministic chaos. Robotics
and Computer-Integrated Manufacturing, 4, 129-134.
Hastings, W. F., Oxley, P. L. B. and Stevenson, M. G.
(1971) Proceedings of the 12th International Machine
Design and Research Conference, Manchester,
(MacMillan).
Hamed, M., Firooz, B. N., Mohammad, R. M. and
Mohammad, T. A. (2010). Nonlinear behaviour of
regenerative chatter in turning process with a worn
tool: Forced oscillation and stability analysis.
Mechanism and Machine Theory, 45, 1050-1066.
Powalka, B., Pajor, M. and Berczynski, S. (2009).
Identification of nonlinear cutting process model in
turning. Advances in Manufacturing Science and
Technology, 33(3), 17-25.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
504