TYPE-1 AND TYPE-2 FUZZY CONTROL OF AN ANTI-LOCK
BREAKING SYSTEM (ABS) AND EVALUATION
OF ITS PERFORMANCES
Ayse Cisel Aras
1
, Yesim Oniz
1
, Okyay Kaynak
1
and Rahib Abiyev
2
1
Department of Electrical and Electronics Engineering, Bogazici University, Istanbul, Turkey
2
Department of Computer Engineering, Near East University, Lefkosa, North Cyprus
Keywords:
Antilock braking system, Type-1 fuzzy neuro system, Type-2 fuzzy neuro system, Gradient descent algorithm.
Abstract:
The control of nonlinear systems is a challenging task in control engineering and the use of type-1 Fuzzy
Logic Controllers (FLCs) has been proposed as a possible approach. However, traditional type-1 FLCs can
prove to be inadequate in dynamically unstructured environments that include large amount of uncertainties.
Under such circumstances, type-2 fuzzy logic controllers can be a viable alternative. In this paper, an Anti-
Lock Breaking System (ABS) is controlled both by a type-1 and an interval type-2 fuzzy logic controller
with and without noisy input measurement. The performances of both controllers are approximately the same
without noise in the input measurement. However, with noisy input measurements, interval type-2 fuzzy logic
controller results in better performance, indicating its superiority when there exist considerable amount of
uncertainties in the system to be controlled.
1 INTRODUCTION
Type-1 Fuzzy Logic Systems (T1-FLSs) were first in-
troduced by Zadeh in 1965, and since then the area
has drawn the interest of many scientists and been
extensively used for modeling and control purposes.
In literature, there are noteworthy studies that have
used type-1 Fuzzy Logic Controllers (FLCs) as ref-
erenced in a recent survey paper (Precup and Hellen-
doorn, 2011).
In most real world applications, the control engi-
neers are confronted with uncertainties and imprecise
information due to the internal and the external dy-
namics of the system to be controlled. Type-1 fuzzy
logic controllers may prove to be inefficient in han-
dling these kinds of uncertainties. To overcome the
problem, the use of type-2 FLCs is suggested in the
literature and many successful applications are re-
ported (Hagras, 2007), (Liang and Mendel, 2000).
Most of these are based on interval type-2 (IT2) struc-
tures (Abiyev and Kaynak, 2010),(Castillo and Melin,
2008).
In this study, uncertainty and noise handling capa-
bility of the considered IT2 FLCs is investigated. The
rule-base of IT2 Fuzzy Neuro System (FNS) structure
is of TSK type. The antecedent part of the fuzzy IF-
THEN rules is composed of interval type-2 member-
ship functions and the consequent part is a first order
polynomial. The design parameters in the antecedent
part are the centers and the standard deviations of the
Gaussian membership functions. Their means are as-
sumed to be uncertain. The design parameters in the
consequent part are the coefficients of the first order
polynomial. These parameters of the structure are
tuned by using gradient descent algorithm.
In Section 2, the mathematical description of the
ABS system used as the test bed is presented. In Sec-
tion 3, the structure of the type-2 fuzzy neural system
is described and parameter update rules are derived.
The simulation studies carried out on the ABS system
are presented in Section 4. In Section 5, an analysis
of the results is given and the further work in the area
is discussed.
2 THE MATHEMATICAL
DESCRIPTION OF ABS
SYSTEM
To derivethe mathematical model of the ABS, the free
body diagram of the quarter vehicle model shown in
503
Cisel Aras A., Oniz Y., Kaynak O. and Abiyev R..
TYPE-1 AND TYPE-2 FUZZY CONTROL OF AN ANTI-LOCK BREAKING SYSTEM (ABS) AND EVALUATION OF ITS PERFORMANCES.
DOI: 10.5220/0003645505030508
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICM-2011), pages 503-508
ISBN: 978-989-8425-74-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

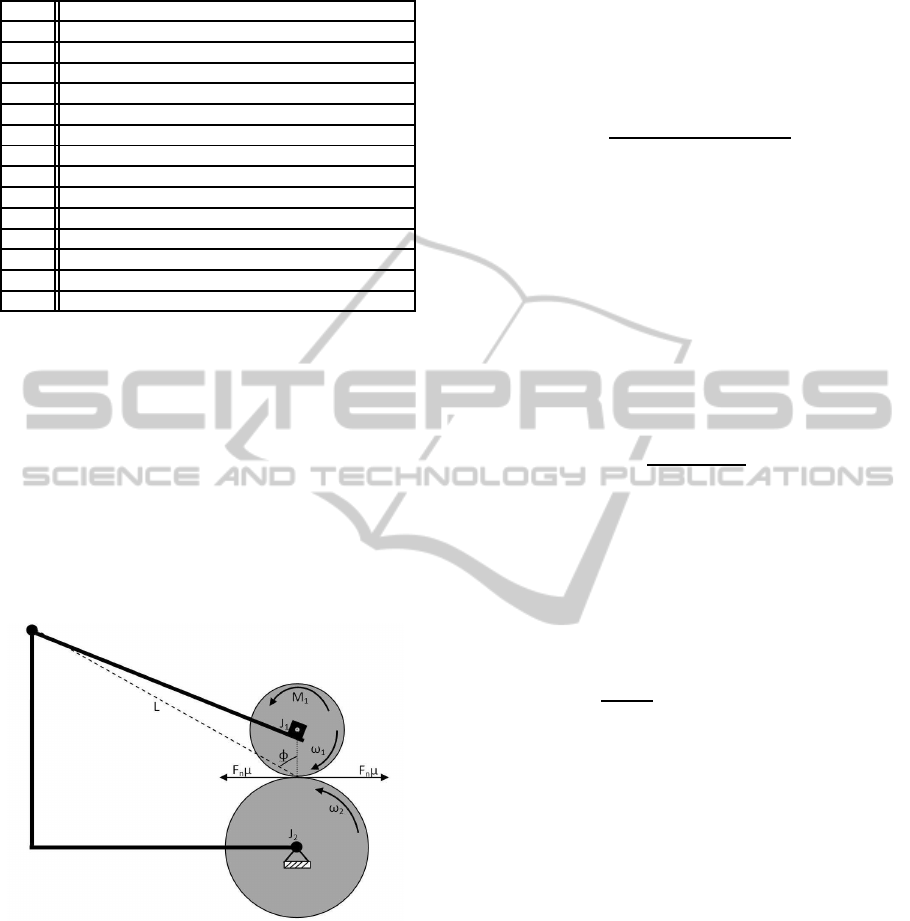
Table 1: System Parameters.
ω
1
Angular velocity of the upper wheel
ω
2
Angular velocity of the lower wheel
T
B
Braking torque
r
1
Radius of the upper wheel
r
2
Radius of the lower wheel
J
1
Moment of inertia of the upper wheel
J
2
Moment of inertia of the lower wheel
d
1
Viscous friction coefficient of the upper wheel
d
2
Viscous friction coefficient of the lower wheel
F
n
Total normal load
µ Road adhesion coefficient
λ Wheel slip
F
t
Road friction force
M
10
Static friction of the upper wheel
M
20
Static friction of the lower wheel
Fig. 1 is considered. The model is quite simple, but
it maintains the fundamental characteristics of a real
system. The lower wheel imitates the relative road
motion, whereas the upper wheel, mounted to the bal-
ance lever, animates the wheel of the vehicle. Several
assumptions are made in deriving the dynamic equa-
tions of the system: The lateral and vertical motions
of the vehicle have been neglected and only the longi-
tudinal dynamics have been considered. Additionally,
it is assumed that there is no interaction between the
four wheels of the vehicle.
Figure 1: Schematic view of experimental setup.
Regarding Fig.1, three torques act on the upper
wheel. These are the braking torque, the friction
torque in the upper bearing, and the friction torque
among the wheels. Similarly, two torques act on the
lower wheel, which are the friction torque in the lower
bearing and the friction torque between these wheels.
For braking, a torque is applied to the upper wheel,
which causes the wheel to slow down. According to
the Newton’s second law, the equation of the motion
of the system can be written as:
J
1
˙
ω
1
= F
t
r
1
− (d
1
ω
1
+ M
10
+ T
B
) (1)
J
2
˙
ω
2
= −(F
t
r
2
+ d
2
ω
2
+ M
20
) (2)
In these equations F
t
can be stated as
F
t
= µ(λ)F
n
(3)
The normal force, F
n
, is computed with the following
formula:
F
n
=
d
1
ω
1
+ M
10
+ T
B
+ M
g
L(sinφ− µ(λ) cosφ)
(4)
In Eq. (4), L is the distance between the contact point
of the wheels and the rotational axis of the balance
lever and Φ corresponds to the angle between the nor-
mal in the contact point and the line L. During driv-
ing, the speed of the vehicle and the rotational ve-
locity of the wheel have matching values. However,
during braking, the braking torque is generated at the
interface between the wheel and road surface, which
causes the wheel speed to decrease. Consequently, the
wheel speed will tend to be lower than vehicle speed.
The parameter used to specify this difference in these
velocities is called wheel slip and denoted by λ.
λ =
r
2
ω
2
− r
1
ω
1
r
2
ω
2
(5)
A zero wheel slip means that the wheel velocity is
equal to the speed of the car, whereas a ratio of one in-
dicates that the wheel is not rotating, but the car is still
moving, i.e. the wheels are skidding on the road and
the vehicle is no more steerable. The road adhesion
coefficient is a nonlinear function of some physical
variables including wheel slip and it can be approxi-
mated by the following formula (Inteco, 2007):
µ(λ) =
c
4
λ
p
a+ λ
p
+ c
3
λ
3
+ c
2
λ
2
+ c
1
λ (6)
The resulting road adhesion coefficient vs. wheel slip
curve is presented in Fig. 2. As can be seen from this
figure, a wheel slip value of 0.2 corresponds to the
maximum value of the road adhesion coefficient.
The numerical values used in this study for the
simulations are:
r
1
= 0.0995(m)
r
2
= 0.0990(m)
φ = 65.61(
◦
)
L = 0.37(m)
J
1
= 0.00753(kgm
2
)
J
2
= 0.0256(kgm
2
)
d
1
= 0.00011874(kgm
2
/s)
d
2
= 0.00021468(kgm
2
/s)
M
10
= 0.0032(Nm)
M
20
= 0.0925(Nm)
c
1
= −0.04240011450454,
c
2
= 0.00000000029375,
c
3
= 0.03508217905067,
c
4
= 0.40662691102315,
a = 0.00025724985785, and
p = 2.09945271667129.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
504

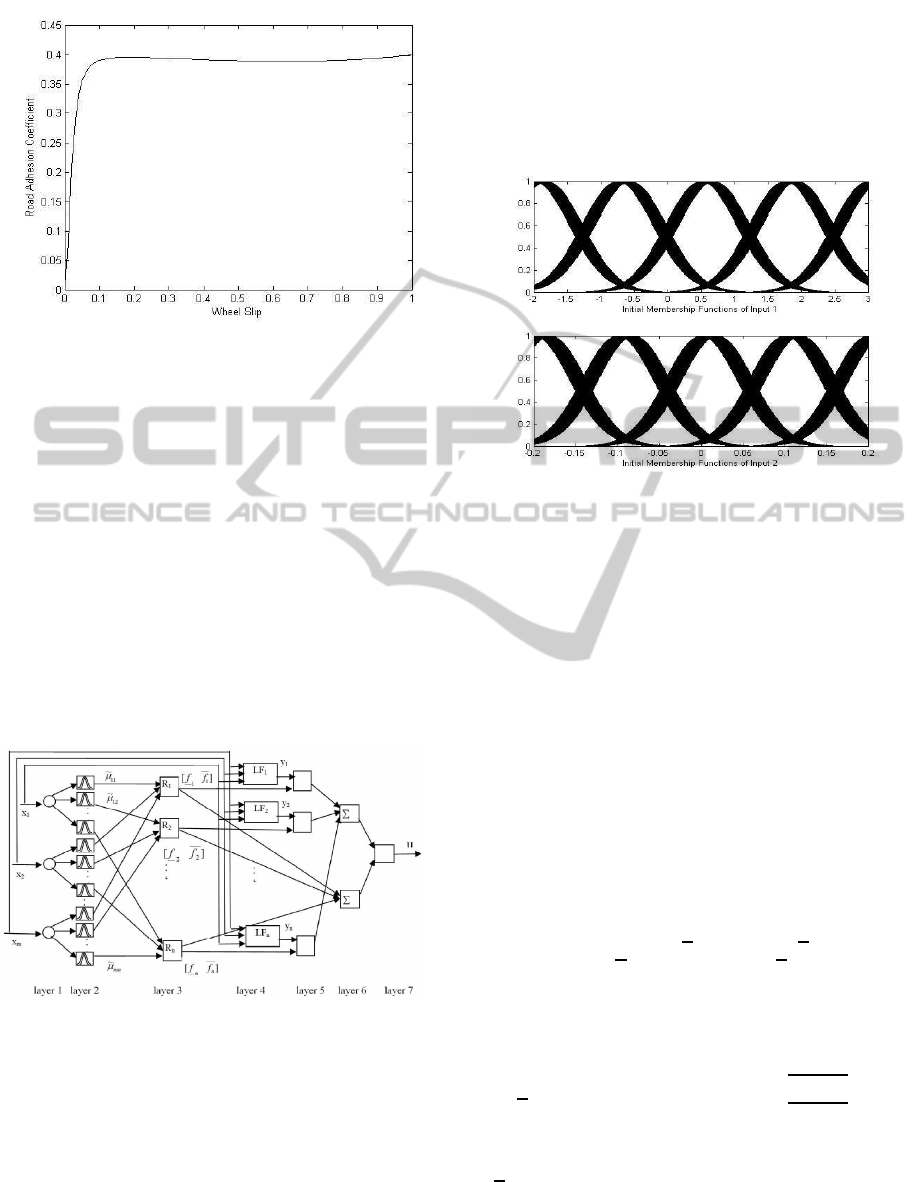
Figure 2: Road adhesion coefficient vs. wheel slip.
3 THE THEORETICAL AND
MATHEMATICAL
BACKGROUND OF T2-FNS
In real world applications, systems experience many
uncertainties due to the dynamically unstructured en-
vironments. Traditional fuzzy logic systems may not
be able to handle these kind of uncertainties. In this
study a type-2 fuzzy-neuro structure is used as the
controller of a system which has two inputs, the error
(e) and the derivative of the error (△e). The structure
of the MISO (multi-input, single-output) neuro fuzzy
controller is given in Fig. 3.
Figure 3: The structure of neuro-fuzzy inference system.
This structure is constructed as a IT2 TSK fuzzy
logic system. Such systems are divided in the lit-
erature into three models depending on the types of
membership functions on the antecedent and the con-
sequent parts of the fuzzy IF-THEN rules (Liang and
Mendel, 1999). This work focusses on the second
model.
In Fig. 3, the first layer of the network is fed by the
external input signal, X = x
1
,x
2
,...,x
n
. In the second
layer, the input space is defined by using Gaussian
membership functions with uncertain mean which are
initially distributed onto the input domain equally as
shown in Fig. 4.
Figure 4: Initial interval type-2 Gaussian membership func-
tions with uncertain mean.
The fuzzy IF-THEN rule structure has the follow-
ing form:
IF x
1
is
˜
˜
A
1j
and...and x
m
is
˜
˜
A
mj
THEN y
j
is
m
∑
i=1
w
ij
x
i
+ b
j
(7)
where x
i
(i = 1,...,m) are the input variables, y
j
( j =
1,...,n) are the output variables which are the linear
functions. The antecedent part of the rule is composed
of interval type-2 fuzzy sets,
˜
˜
A
ij
for the j-th rule of the
i-th input, and the consequent part of the rule is a first
order polynomial with the coefficients, w
ij
and b
j
.
The second layer in Fig. 3, the upper and lower
membership functions degrees are determined by us-
ing Eq. (8).
µ
˜
A
i
k
= [µ
˜
A
i
k
(x
k
),µ
˜
A
i
k
(x
k
)] = [µ
i
,µ
i
] (8)
Lower and upper membership functions between
i
th
input and j
th
hidden neurons of layer 3 can be
given as follows:
µ
ij
(x) =
(
G(c2
ij
,σ
ij
,x
i
) x
i
≤
c1
ij
+c2
ij
2
G(c1
ij
,σ
ij
,x
i
) x
i
>
c1
ij
+c2
ij
2
µ
ij
(x) =



G(c1
ij
,σ
ij
,x
i
) x
i
< c1
ij
1 c1
ij
≤ x
i
≤ c2
ij
G(c2
ij
,σ
ij
,x
i
) x
i
> c2
ij
(9)
TYPE-1 AND TYPE-2 FUZZY CONTROL OF AN ANTI-LOCK BREAKING SYSTEM (ABS) AND EVALUATION
OF ITS PERFORMANCES
505

where G(c
ij
,σ
ij
,x
i
) is determined as:
G(c
ij
,σ
ij
,x
i
) = exp

−
1
2
(x
i
− c
ij
)
2
σ
2
ij

(10)
The firing strengths of the rules are calculated by
using the prod t-norm operator at the third layer.
f = µ
˜
A
1
(x
1
) ∗ ··· ∗ µ
˜
A
n
(x
n
) (11)
f = µ
˜
A
1
(x
1
) ∗ ··· ∗ µ
˜
A
n
(x
n
) (12)
The output of the consequent part of the each rule
is calculated at the fourth layer as follows:
y
j
=
m
∑
i=1
w
ij
x
i
+ b
j
(13)
The type reduction and the defuzzification proce-
dures are realized at the fifth, the sixth and the seventh
layers of the neuro-fuzzy structure. The defuzzified
output of the type-2 TSK fuzzy system is determined
by using the inference engine proposed in (Biglarbe-
gian et al., 2010), and has the following form:
u =
p
∑
N
j=1
f
j
y
j
∑
N
j=1
f
j
+
q
∑
N
j=1
f
j
y
j
∑
N
j=1
f
j
(14)
where f
j
and f
j
are the lower and upper firing
strength of each rule, respectively. p and q are the de-
sign parameters that weight the sharing of lower and
upper firing levels of each fired rule, N is the number
of rules.
4 TRAINING OF THE T2-FNS
After the output of the system is calculated, the gra-
dient descent algorithm is applied to tune the design
parameters of the system which are the center and the
standard deviation of the membership functions at the
antecedent part, the coefficients of the first order poly-
nomial at the consequent part, p and q values in Eq.
(14).
Initially, the output error is determined as follows:
E =
1
2
O
∑
i=1
(u
d
i
− u
i
)
2
(15)
where O is the number of output, u
d
i
and u
i
are the
desired and the actual output of the network, respec-
tively.
The parameters at the antecedent part of the rules,
c1
ij
, c2ij, σ
ij
and the parameters at the consequent
part of the rules, w
ij
, b
j
are tuned by using gradient
descent algorithm as follows:
w
ij
(t + 1) = w
ij
(t) − γ
∂E
∂w
ij
;b
j
(t + 1) = b
j
(t) − γ
∂E
∂b
j
(16)
c1
ij
(t+1) = c1
ij
(t)−γ
∂E
∂c1
ij
;c2
ij
(t+1) = c2
ij
(t)−γ
∂E
∂c2
ij
(17)
σ
ij
(t + 1) = σ
ij
(t) − γ
∂E
∂σ
ij
(18)
where γ is the learning rate. The derivatives in Eqs.
16-18 are determined as follows:
∂E
∂w
ij
=
∂E
∂u
∂u
∂y
j
∂y
j
∂w
ij
(19)
∂E
∂b
j
=
∂E
∂u
∂u
∂y
j
∂y
j
∂b
j
(20)
∂E
∂σ
ij
=
∑
j
∂E
∂u

∂u
∂f
j
∂f
j
∂µ
ij
∂µ
ij
∂σ
ij
+
∂u
∂f
j
∂f
j
∂µ
ij
∂µ
ij
∂σ
ij

∂E
∂c1
ij
=
∑
j
∂E
∂u

∂u
∂f
j
∂f
j
∂µ
ij
∂µ
ij
∂c1
ij
+
∂u
∂f
j
∂f
j
∂µ
ij
∂µ
ij
∂c1
ij

∂E
∂c2
ij
=
∑
j
∂E
∂u

∂u
∂f
j
∂f
j
∂µ
ij
∂µ
ij
∂c2
ij
+
∂u
∂f
j
∂f
j
∂µ
ij
∂µ
ij
∂c2
ij

where
∂E
∂u
= u(t)−u
d
(t);
∂u
∂f
j
= p
y
j
− u
∑
n
j=1
f
j
;
∂u
∂f
j
= q
y
j
− u
∑
n
j=1
f
j
u =
∑
n
j=1
f
j
y
j
∑
n
j=1
f
j
;u =
∑
n
j=1
f
j
y
j
∑
n
j=1
f
j
(21)
t-norm prod operator has the following form.
∂f
j
∂µ
ij
=
N1
∏
k = 1
k 6= i
µ
kj
(22)
∂f
j
∂µ
ij
=
N1
∏
k = 1
k 6= i
µ
kj
(23)
where i =,...,N1, k = 1,...,N1, and j = 1, ...,N2.
Then,
∂µ
j
(x
i
)
∂c1
ij
=





G(c1
ij
,σ
ij
,x
i
)
(x
i
−c1
ij
)
σ
2
ij
, x
i
< c1
ij
0, c1
ij
≤ x
i
≤ c2
ij
0, x
i
> c2
ij
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
506

∂µ
j
(x
i
)
∂c1
ij
=
(
0, x
i
≤
c1
ij
+c2
ij
2
G(c1
ij
,σ
ij
,x
i
)
(x
i
−c1
ij
)
σ
2
ij
), x
i
>
c1
ij
+c2
ij
2
(24)
∂µ
j
(x
i
)
∂c2
ij
=





0, x
i
< c1
ij
0, c1
ij
≤ x
i
≤ c2
ij
G(c2
ij
,σ
ij
,x
i
)
(x
i
−c2
ij
)
σ
2
ij
, x
i
> c2
ij
∂µ
j
(x
i
)
∂c2
ij
=
(
G(c2
ij
,σ
ij
,x
i
)
(x
i
−c2
ij
)
σ
2
ij
), x
i
≤
c1
ij
+c2
ij
2
0, x
i
>
c1
ij
+c2
ij
2
(25)
∂µ
j
(x
i
)
∂σ
ij
=







G(c1
ij
,σ
ij
,x
i
)
(x
i
−c1
ij
)
2
σ
3
ij
, x
i
< c1
ij
0, c1
ij
≤ x
i
≤ c2
ij
G(c2
ij
,σ
ij
,x
i
)
(x
i
−c2
ij
)
2
σ
3
ij
, x
i
> c2
ij
∂µ
j
(x
i
)
∂σ
ij
=



G(c2
ij
,σ
ij
,x
i
)
(x
i
−c2
ij
)
2
σ
3
ij
), x
i
≤
c1
ij
+c2
ij
2
G(c1
ij
,σ
ij
,x
i
)
(x
i
−c1
ij
)
2
σ
3
ij
), x
i
>
c1
ij
+c2
ij
2
(26)
The parameters p and q enable us to adjust the lower
and upper portions of the final output in Eq. (14). The
optimization algorithm for these parameters is given
by the following equations. The initial value for both
parameters is taken as 0.5.
p(t + 1) = p(t) − γ
∂E
∂p
(27)
q(t + 1) = q(t) − γ
∂E
∂q
(28)
where
∂E
∂p
= (u− u
d
)
f
j
∑
n
j=1
f
j
(29)
∂E
∂q
= (u− u
d
)
f
j
∑
n
j=1
f
j
(30)
5 SIMULATION RESULTS
A number of simulation studies are carried out with
type-1 and type-2 FNS controllers acting on the ABS
system described and the results obtained are com-
pared. The block diagram of the type-2 FNS system
is shown in Fig. 5. As has been discussed earlier, the
FNS block has two inputs, e is the error and △e is
the derivative of the error. g is the reference signal,
u is the control input signal and y is the output of the
system.
In the simulations, the sampling time is set to 1ms.
The rotational velocity of the upper and lower wheels
before the braking operation is selected 250 rad/s.
The reference wheel slip is set to 0.2 which corre-
sponds to the peak value of µ − λ. In order to de-
termine the efficiency and the accuracy of the pro-
posed controller two sets of simulation studies have
been conducted. In the first study, the performances
of both controllers are tested without noise in the in-
put measurement. Then, in the second set of simula-
tions, the noise effect is included as shown in Fig. 6.
The signal-to-noise ratio (SNR) is about 17dB.
Figure 5: The structure of type-2 Neuro Fuzzy System.
The initial membership functions for error and the
derivative of the error are distributed equally onto the
input domain. The initial weights of the neural net-
work are selected randomly.
Table 2 shows Root Mean Squared Error (RMSE)
values to compare the performances of the both algo-
rithms.
Figure 6: The noisy input measurement for the two cases.
Table 2: Root Mean Squared Error values of the type-1 and
type-2 FNS algorithms.
without Noise with Noise
T1 FNS 1.731 2.419
IT2 FNS 1.714 2.197
TYPE-1 AND TYPE-2 FUZZY CONTROL OF AN ANTI-LOCK BREAKING SYSTEM (ABS) AND EVALUATION
OF ITS PERFORMANCES
507

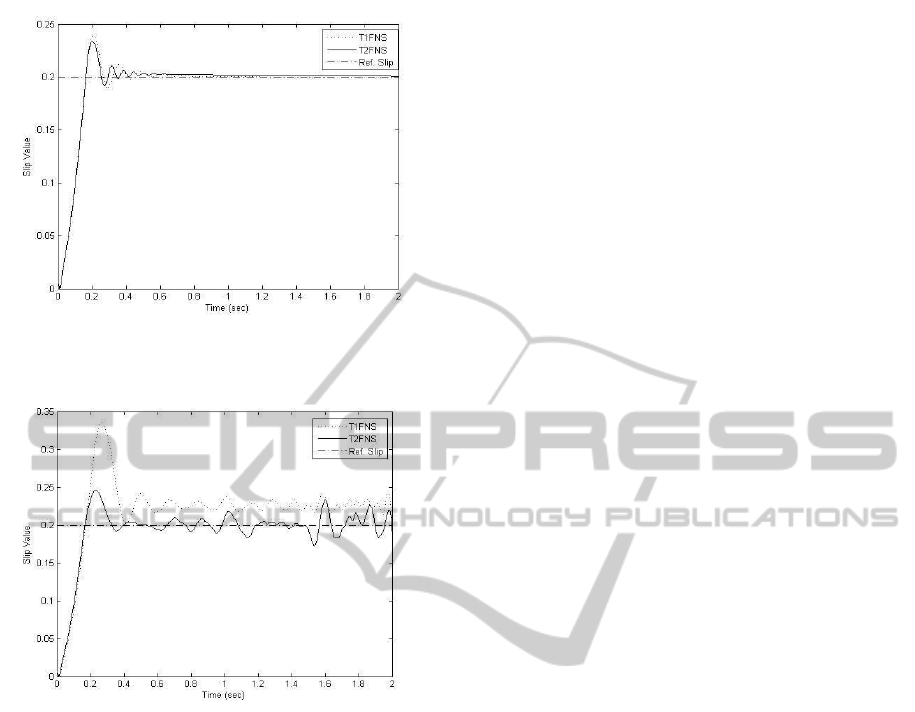
Figure 7: Wheel slip of type-1 and type-2 FNS without
noise in the input measurement.
Figure 8: Wheel slip of type-1 and type-2 FNS with noise
in the input measurement.
6 CONCLUSIONS
In this paper, two different structures, a type-1 and a
type-2 structure are used to control ABS system. The
functions of the layers in each structure are explained
in detail and the parameter update rules of the struc-
tures are given which are based on gradient descent
algorithms.
A number of simulation studies are carried out.
Firstly, it is assumed that the input measurements are
not corrupted with noise. The results indicate that
both controllers have similar responses. However,
in real life, the measurements usually include some
level of noise. To simulate this, a band limited white
noise is added to the slip measurement. In this case,
it can be seen from Fig. 8 that type-2 FNS outper-
forms type-1 FNS. It can therefore be concluded that
type-2 FNS structure results in a better performance
when there exists uncertainties. Encouraged by the
simulation results, an experimental study is about to
be launched.
ACKNOWLEDGEMENTS
The authors would like to acknowledge TUBITAK
Grant No: 107E284 and Bogazici University Project
Grant No: 08A204.
REFERENCES
Abiyev, R. and Kaynak, O. (2010). Type-2 fuzzy neu-
ral system structure for identification and control of
time-varying plants. In IEEE Trans. Indust. Electron.
vol.57, no.12, pp.4147-4159.
Biglarbegian, M., Melek, W., and Mendel, J. (2010). On
the stability of interval type-2 TSK fuzzy logic control
systems. In IEEE Transactions on Systems, Man, and
Cybernetics, Part B: Cybernetics. vol.40, issue 3, pp.
798-818.
Castillo, O. and Melin, P. (2008). Type-2 Fuzzy Logic: The-
ory and Applications, Studies in Fuzziness and Soft
Computing. Springer, Vol. 223.
Hagras, H. (2007). Type-2 FLCs: A new generation of
fuzzy controllers. In IEEE Computational Intelligence
Magazine. vol.2, pp.30-43.
Inteco (2007). The Laboratory Antilock Braking System
Controlled from PC. Inteco Ltd., Poland, user’s man-
ual edition.
Liang, Q. and Mendel, J. (1999). An introduction to type-
2 TSK fuzzy logic systems. In IEEE International
Fuzzy Systems Conference. vol.3, pp. 1534-1539.
Liang, Q. and Mendel, J. (2000). Interval type-2 fuzzy logic
systems: Theory and design. In IEEE Transactions on
Fuzzy Systems. vol.8, pp.535-550.
Precup, R. and Hellendoorn, H. (2011). A survey on indus-
trial applications of fuzzy control. In Computers in
Industry. vol.62, pp.213-226.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
508