A COMPARATIVE STUDY OF DIFFERENT CHIP SEPARATION

APPROACHES FOR NUMERICAL MODELING OF

ORTHOGONAL CUTTING

Bo Hou

, Yong-fu Wu

, Shu-hui Li

1,2

, Zhong-qin Lin

1,2

and Zhong-qi Yu

1,2

Shanghai Key Laboratory of Digital Autobody Engineering, Shanghai Jiao Tong University

800 Dongchuan RD., Shanghai, China

State Key Laboratory of Mechanical System and Vibration, Shanghai, China

Keywords: Dry cutting, Modelling, ALE, Damage evolution, Residual stress.

Abstract: Numerical cutting modelling gives access to thermo-mechanical field such as stress, strain and temperature

that are difficult to obtain through experiments, thus provides a unique insight and helps to improve design

quality and shorten design cycle. Chip separation is one of the most important issues in cutting simulation

because of its significant influence on chip formation, stress and temperature predictions. Modelling of an

orthogonal cutting process using ABAQUS/explicit is presented. Two kinds of chip separation approaches

are compared, a partial damage zone (PDZ) and an Arbitrary-Lagrangian-Eulerian (ALE) based approach,

with the aim to characterize the effect on chip formation, cutting force, temperature and residual stress. ALE

and PDZ methods predict the similar cutting force and temperature results, and they also predict different

chip formations and residual stress profiles. The predictions are analysed and possible reasons are discussed.

1 INTRODUCTION

Numerical cutting modelling are more and more

essential in predicting chip formation, cutting forces,

distributions of strain, strain rate, stress, and cutting

temperature. Therefore, it provides a unique insight

for fundamental understanding of the machining

process, which leads to proper choice or design of

cutting tools, fixture, spindle, feed, and reduction of

lengthy and costly design iterations experimentation

required for process optimization.

Reliable cutting simulation heavily depends on

the chip separation approaches, which are based on

three main formulations. The first one is the

Lagrangian formulation, in which the elements are

attached to the material. Shet and Deng (2003:573-

583) applied Lagrangian model for orthogonal

cutting simulation, in which the chip separation was

modelled by nodal release based on critical stress

criterion. In the study of Hortig and Svendsen

(2007:66-76), the continuous chip was formed along

a predefined separation path based on the fracture

criterion and element deletion. Ng et al (2002:301-

329) and Mabrouki et al (2008:1187-1197) studied

saw-tooth chip formation with a predefined

separation path, as well as a damage law for

modelling fragmented chip behaviour. The chip

separation approaches based on Lagrangian

formulation are generally base on partial damage

zone (PDZ) corresponding to the trajectory of the

tool-tip. However, the PDZ must be predefined

which is difficult for 3D milling modelling.

Furthermore, the global damage zone (GDZ)

approach is applied for chip separation, in which

each element is assessed for damage over the mesh

and all time increments. Pantalé et al (2004:4383-

4399) and Anurag et al (2009:303-317) studied

orthogonal and 3D milling process using GDZ

approach with no pre-defined sacrificial element or

zipped nodes to be split.

The Eulerian formulation, in which the element

is not attached to the material, handles material flow

around tool tip without the need to define a failure

criterion (Nasr, Ng and Elbestawi, 2007:401-411).

However, the chip shape has to be known a priori,

which represents a huge drawback. Furthermore,

residual stress cannot be estimated because the

material elastic behaviour is not considered

(Movahhedy, Gadala and Altintas, 2000:267-275).

Studies using Eulerian formulation for chip

separation are reported by Kim et al (1999:45-55)

458

Hou B., Wu Y., Li S., Lin Z. and Yu Z..

A COMPARATIVE STUDY OF DIFFERENT CHIP SEPARATION APPROACHES FOR NUMERICAL MODELING OF ORTHOGONAL CUTTING.

DOI: 10.5220/0003646004580464

In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SDDOM-2011), pages

458-464

ISBN: 978-989-8425-78-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

and Strenkowski et al (2002:723-731).

The Arbitrary-Lagrangian-Eulerian (ALE)

formulation combines the features of Lagrangian

and Eulerian analysis. The Eulerian technique is

perfect for modelling the material flow around tool

tip, while the Lagrangian technique is suitable for

modelling the unconstrained material flow at the free

boundaries. Therefore, the thermo-mechanical field

surrounding the tool tip can be analysed more

reliably, together with the absence of separation

criterion, which is always necessary in Lagrangian

model. As a result, the residual stress can be

calculated with enough accuracy which is

impossible in Eulerian models (Nasr, Ng and

Elbestawi, 2008:149-161). However, serrated chip

cannot be modelled with this technique. Another

drawback is the necessity to precisely define the

previous geometry of the chip.

Different chip separation approaches are adopted

in cutting simulations for different purposes, such as

prediction of chip formation, cutting force and

residual stress. However, a systematic comparison of

them has not been reported yet. It is difficult to

estimate the practical effects of different approaches

for the same material and cutting process. This paper

aims to estimate PDZ and ALE based chip

separation approaches in terms of chip formation,

stress, temperature distribution and cutting force

prediction during orthogonal cutting of an aeronautic

aluminium alloy Al7050-T7451, which is generally

used as the structural material of aircraft.

2 NUMERICAL MODEL

2.1 Material Constitutive Model

The Johnson-Cook material model is utilized.

Assuming a von Mises type yield criterion and an

isotropic strain hardening rule, the flow stress is

given by

()

0melt0

1ln 1

AB C

σε

⎡⎤

⎛⎞⎛⎞

−

⎢⎥

=+ + −

⎜⎟⎜⎟

−

⎢⎥

⎝⎠⎝⎠

⎣⎦



(1)

where

is the equivalent plastic strain.



and



are the equivalent plastic strain rate and a reference

strain rate, respectively. T, T

and T

melt

stand for

temperature, reference temperature and melting

temperature, respectively. A, B, C, m and n are

material parameters.

There are two popular experimental methods to

obtain the flow stress data under cutting condition:

Split Hopkinson pressure bar (SHPB) (Lennon and

Ramesh, 1998:1279-1292) and Orthogonal cutting

(OC) (Sartkulvanich, Koppka and Altan, 2004:61-

71). Fu (2007:30) combined the SHPB and OC

methods to determine the material parameters of Eq.

1. For Al7050-T7451, the physical properties and

Johnson-Cook model parameters are shown in Table

1 and Table 2, respectively.

Table 1: Physical properties of workpiece (Al7050-T7451)

and Tool material (YG6).

Physical

parameter

Workpiece

(Al7050-T7451)

Tool

(YG6)

Density, ρ

(kg/m3)

2800 14600

Elastic modulus,

E (GPa)

69.35(20℃),

63(100℃),

57.09(200℃),

44.57(300℃)

630

Poisson’s ratio, v 0.33 0.21

Specific heat, C

(J/kg℃)

888(50℃),

904(100℃),

988(150℃),

1004(204℃),

1047(260℃)

400

Thermal

conductivity,

λ(W/m℃)

134(50℃),

142(100℃),

147(125℃),

176(200℃)

79.6

Linear Expansion

coefficient,

α (10

-6

/℃)

23.6(100℃),

23.3(125℃),

23.5(150℃),

24(200℃)

melt

(℃) 630℃

(℃) 25℃

Table 2: Johnson-Cook constitutive model parameters of

Al 7050-T7451 (Fu, X.L., 2007).

A (MPa) B (MPa) C n m



463.4 319.5 0.027 0.32 0.99 1

2.2 ALE Chip Separation Approach

The ALE model is divided in several zones, and uses

sliding, Lagrangian and Eulerian contours allowing

the material to flow across an internal Eulerian zone

surrounding the tool tip.

As shown in Figure 1, Zones 1, 2 and 3 combine

Lagrangian/Eulerian boundaries with sliding

boundaries, where the material is allowed to flow

tangentially to the contour and not allowed to go

across this boundary. At Eulerian zone 4, it is

considered as a tube with one entrance and two

exits, and the material enters on the left-hand

A COMPARATIVE STUDY OF DIFFERENT CHIP SEPARATION APPROACHES FOR NUMERICAL MODELING

OF ORTHOGONAL CUTTING

459

boundary and exits at the right-hand boundary and at

the top surface. In order to retain the Eulerian

boundaries, adaptive mesh constraints are endowed

with both the X and Y direction of the zone 4.

The geometry of the baseline model with zero

rake angle and cutting edge radius 0.02mm of tool,

cutting depth 0.1mm and cutting width 1.5mm of

workpiece is established. The tool is fixed and the

cutting speed is applied to the workpiece.

Continuous chip formation is assumed. The material

flowed around the tool tip as if it is a fluid. In other

words, there is no need to define a failure criterion.

Figure 1: Illustration of ALE model.

2.3 PDZ Chip Separation Approach

Figure 2 illustrates the geometry of the orthogonal

cutting model with a predefined cutting path, which

is composed of four parts: (1) tool, (2) chip, (3) tool-

tip passage zone and (4) workpiece. A chamfer is

designed on part 2 to avoid distortion problems at

the beginning of calculation. The centre of the tool

tip is placed exactly at the middle height of part 3.

The length and width of parallelogram mesh are set

less than 20μm due to high shear localization.

Figure 2: Illustration of ALE model.

The separation of the chip from the workpiece is

based on a shear failure module which is applied to

part 3. The shear failure module is based on the

effective plastic strain

. When any element

reaches the failure plastic strain value

, the

damage parameter D, in Eq. 2 equals to one. When

this occurs, the corresponding element will be

deleted. The workpiece is fixed and the cutting

speed is applied to the tool. Continuous chip

formation is assumed. The tool geometry, cutting

depth and cutting width of the workpiece is exactly

the same as that used in ALE model.

(2)

2.4 Contact Modelling

The modified Coulomb friction model is adopted to

describe the sliding and sticking phenomenon on the

tool rake face. Figure 3 shows the characteristic of

the model. Sticking or sliding friction conditions

along the tool-chip interface are dependent on the

shear stress magnitude. Sticking will occur at high

contact pressure, as shown in the shaded region.

When the contact pressure is low, as is the case

away from the tool cutting edge, sliding friction will

dominate (as shown in the unshaded region).

Figure 3: Stick-Slip region for the coulomb friction.

The following expression has been applied:

τ = μp when μp < τ

max

(sliding) (3)

τ = τ

max

when μp ≥ τ

max

(sticking) (4)

where τ, p are the friction stress and the contact

pressure on the tool rake face, respectively. τ

max

, is

the maximum shear stress of the material, and μ is

the friction coefficient. In this study, the tendency of

friction coefficient μ with cutting speed is obtained

by the orthogonal cutting tests (Fu, 2007:50).

2.5 Heat Generation

Heat generation during metal cutting is important in

tool wear and plays an important role in surface

integrity and chip formation. The majority of the

heat generated comes from plastic deformation and

friction. The temperature increment associated with

the heat generation are expressed by

⋅∂

Δ=

(5)

Sliding

Eulerian

①

②

③

④

Tool

Workpiece

Lagrangian

Cutting velocity

20μm

Part 3

Part 4

Part 2

Part 1

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

460

Where ΔT is temperature increment, f

is work-heat

convection factor; f

is the conversion efficiency

factor. f

and f

are taken as 0.9.

∂

is the effective

plastic strain increment. ρ and C

are material

density and specific heat. Heat transfer between tool

and workpiece is not considered.

2.6 Analysis

Plane strain conditions are considered (as the

workpiece width is at least ten times the chip

thickness). An explicit resolution method with

dynamic and coupled thermo-mechanical analysis is

performed with CPE4RT element type.

Analysis is carried out in two steps. In the first

step, cutting is modelled at constant cutting speed

and steady state conditions are reached. In the

second step, the workpiece is unloaded and cooled,

and the residual stress profile is obtained.

3 RESULTS AND DISSCUSSION

3.1 Chip Formation

The comparison of the predicted chip and Mises

stress at t=0.075ms and t=0.15ms for ALE and PDZ

methods is shown in Figure 4. The chip curl of the

PDZ method has larger radius than that of ALE

method. Generally, the chip with a longer contact

length with the tool produces a larger curl radius

than that with a shorter contact. As the calculation

time increases, the number of elements of ALE

model in contact with the tool decreases because

they are enlarged as well as the excessive distortion

at the curvature zone of the chip, thus diminishing

the accuracy of the calculation. Indeed, the chip

from the PDZ model has twice longer contact length

than that of ALE model. The chip curl is a key issue

for the design of chip breakers, and good tool

performance from the correct design.

3.2 Cutting Force

Figure 5 illustrates the predicted cutting force and

feed force under different cutting speeds. It is clear

that the predicted cutting force almost yield a similar

pattern that the force magnitude decreases with the

cutting speed. Small discrepancy is found between

the predicted cutting force of the ALE and PDZ

methods, which is less than 30N.

It is found that the predicted feed force of the

ALE model is below that of PDZ model. Larger

(a)

(b)

Figure 4: Chip formation process of (a) ALE, (b) PDZ

method at v=800m/min.

discrepancy between the predicted feed forces is

found when the cutting speed over 800m/min. In

PDZ model, the elements of the separation path are

enlarged to failure which will apply an extra force

perpendicular to the machined surface around the

too-tip. As the cutting speed increases, the feed force

is influenced significantly.

t=0.075ms

t=0.15ms

t=0.075ms

t=0.15ms

A COMPARATIVE STUDY OF DIFFERENT CHIP SEPARATION APPROACHES FOR NUMERICAL MODELING

OF ORTHOGONAL CUTTING

461

(a)

(b)

Figure 5: Predicted (a) cutting force and (b) feed force

results under different cutting speeds.

(a)

(b)

Figure 6: Predicted temperature distributions of (a) ALE,

(b) PDZ, at v=800m/min.

3.3 Stress and Temperature Field

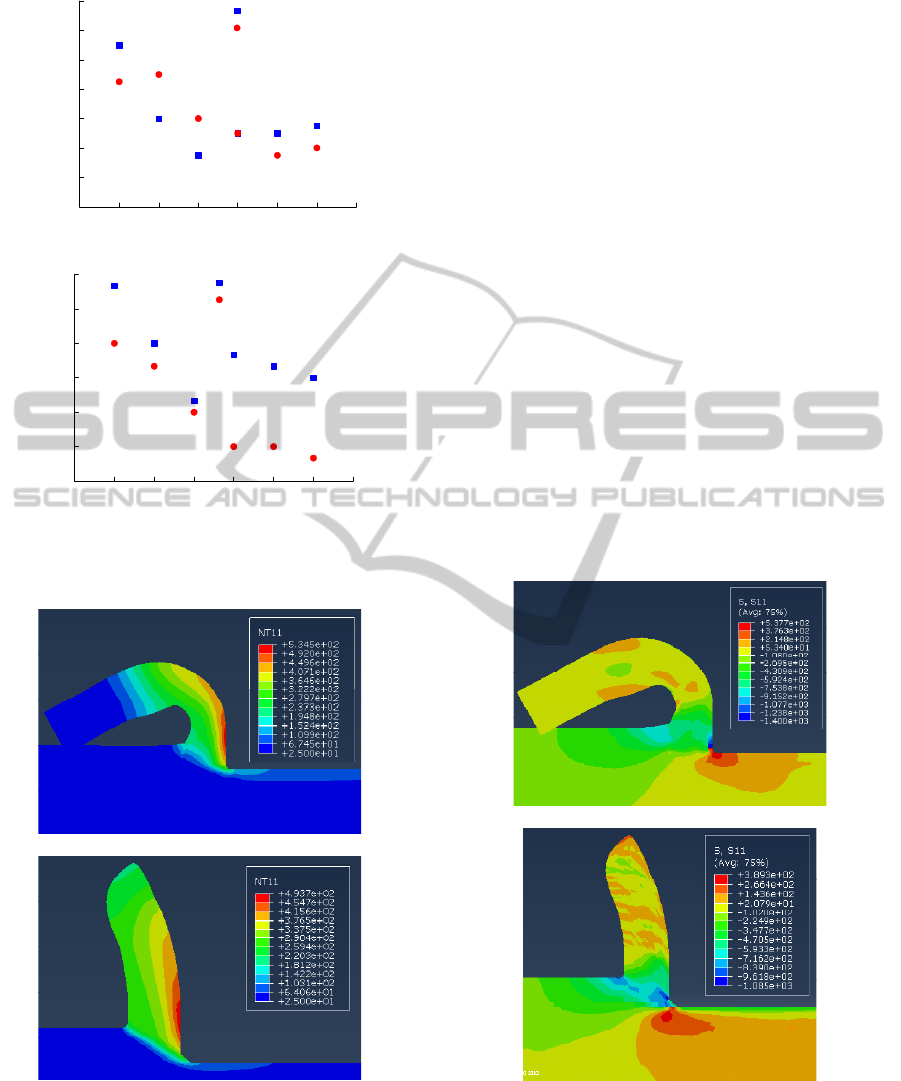
Figure 6 shows the instantaneous temperature fields

at t=0.075ms. The predictions of ALE and PDZ

model have a similar temperature distribution

pattern. The highest temperature region occurs at the

tool-chip interface, i.e., secondary shear zone. The

maximum temperatures are 534.5°C and 493.7°C for

ALE and PDZ model predictions, respectively,

while the average temperature in the shear zone are

131.6°C and 122.6°C for the ALE and PDZ model.

In Figure 7, the stress distributions in the cutting

direction S

at t=0.075ms are depicted. In each case,

the highest stress level is found in the first shear

zone with the peak compressive stress in contact

with the tool tip. The highest value of S

, 1400MPa

is found in the prediction using ALE method, while

1085MPa is found in the prediction using PDZ

method. Moreover, strong stress fields exist in the

zones in front of and behind the tool tip, in which

compressive stress (green zone) dominates the front

zone while tensile stress dominates the back zone

(red zone) due to the effect of tool flank.

However, the stress distribution patterns on the

produced new surface are quite different for ALE

and PDZ methods, which are tensile stress

dominated and compressive stress dominated

respectively.

(a)

(b)

Figure 7: Predicted S

distributions of (a) ALE, (b) PDZ,

at v=800m/min.

3.4 Residual Stress

The effect of chip separation and cutting speeds on

140

160

180

200

220

240

260

280

0 200 400 600 800 1000 1200 1400

Cutting speed V (m/min)

PDZ model

Cutting force (N)

ALE model

0 200 400 600 800 1000 1200 1400

105

Feed force (N)

Cutting speed V (m/min)

PDZ model

ALE model

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

462

the predicted residual stresses in cutting direction

(RS

) is shown in Figure 8.

For each cutting speed, ALE method produces

tensile stress on the surface, and the magnitude of

RS11 decreases within the depth of 100 μm below

the machined surface. Then, the RS

tends to be

constant as the depth over 100μm. This pattern

agrees well with the computed residual stress results

of Nasr (2008:149-161) using ALE method, which

are also verified by the experiments. On the other

hand, PDZ method produces compressive stress on

the surface, and the RS

increases within depth of

100 μm below the machined surface. Then, the RS

tends to be constant as the depth over 100μm.

The effect of cutting speeds on the predicted

is also different for ALE and PDZ methods.

The predicted peak magnitude of RS

by ALE

method decreases as the cutting speed increases,

which is generally reported in literature. On the

other hand, the predicted peak magnitude of RS

PDZ method increases proportionally as the cutting

speed increases.

(a)

(b)

Figure 8: Predicted residual stress profiles of (a) ALE, (b)

PDZ method under different cutting speeds.

The primary cause of residual stress generation is

plastic deformation. In order to explain the different

residual stress predictions, the plastic strain in the

cutting direction (PE11) of the machined surface

around the tool-tip are shown in Figure 9. It is clear

that ALE method produces the compressive strain on

the surface and near-surface layers, with the peak

value of 0.06. But PDZ method produces the tensile

strain with the peak value of 0.01. After the

workpiece is unloaded and cooled, the residual stress

will becomes tensile and compressive dominated,

respectively.

(a)

(b)

Figure 9: Predicted strain distributions of (a) ALE, (b)

PDZ method, at v=800m/min.

The combination of mechanical and thermal

loading produces the strain results, and it is noticed

the cutting force and temperature predictions are

similar for ALE and PDZ methods. It is interesting

that the same thermo-mechanical loading produces

different strain results.

It is noticed that the elements of the separation

path in PDZ model are enlarged to failure which will

drag the element on the new produced surface. As a

result, the tensile dominated strain state is formed.

On the other hand, ALE method handles the material

flow surrounding the tool-tip perfectly, thus the

material exiting at the right-hand boundary of

Eulerian zone is merely affected by the tool flank.

As a result, the compressive dominated strain state is

formed in the prediction of ALE model.

4 CONCLUSIONS

Based on the prediction results and discussions, the

following conclusions are obtained:

0 50 100 150 200 250 300

-100

-50

100

150

200

250

300

V=200m/min

Depth below machined surface (μm)

Residual stress RS

(MPa)

V=400m/min

V=600m/min

V=800m/min

-500

-400

-300

-200

-100

100

200

V=200m/min

V=400m/min

V=600m/min

V=800m/min

Depth below machined surface (μm)

Residual stress RS

(MPa)

0 50 100 150 200 250 300

A COMPARATIVE STUDY OF DIFFERENT CHIP SEPARATION APPROACHES FOR NUMERICAL MODELING

OF ORTHOGONAL CUTTING

463

¾ Chip formation predicted by ALE and PDZ

methods is quite different. ALE method is

difficult to predict reasonable chip formation.

¾ ALE and PDZ methods predict similar cutting

force and temperature predictions.

¾ ALE and PDZ methods predict different

residual stress profiles, and the possible reasons

are discussed through the strain results around

the tool-tip.

ACKNOWLEDGEMENTS

The authors acknowledge the support from the

National Basic Research Program of China

(No.2010CB731703) and National Natural Science

Foundation of China (No.51075267).

REFERENCES

Shet, C., Deng, X., 2003. ‘Residual stress and strain in

othogonal metal cutting’, Int. J. Mach. Tool. Manu,

vol. 43, pp. 573-583.

Hortig, C., Svendsen, B., 2007. ‘Simulation of chip

formation during high-speed cutting’, J. Mater.

Process. Tech, vol. 186, pp. 66-76.

Ng, E-G., El-Wardany, T-I., Dumitrescua, M., and

Elbestawia, M. A., 2002. ‘physics-based simulation of

high speed machining’, Mach. Sci. Technol, vol. 6, no.

3, pp. 301-329.

Mabrouki, T., Girardin, F., Asad, M., and Rigal, J-F., 2008.

‘Numerical and experimental study of dry cutting for

an aeronautic aluminium alloy (A2024-T351)’, Int. J.

Mach. Tool. Manu, vol. 48, pp. 1187-1197.

Pantalé, O., Bacaria, J-L., Dalverny, O., Rakotomalala, R.,

and Caperaa, S., 2004. ‘2D and 3D numerical models

of metal cutting with damage effects’, Comput.

Methods Appl. Mech. Engrg, vol. 193, pp.4383-4399.

Anurag, S., Guo, Y.B., and Horstemeyer, M.F., 2009. ‘The

effect of materials testing modes on finite element

simulation of hard machining via the use of internal

state variable plasticity model coupled with

experimental study’, Comput. Struct, vol. 87, pp. 303-

317.

Nasr, M.N.A., Ng, E-G., and Elbestawi, M.A., 2007.

‘Modelling the effects of tool-edge radius on residual

stresses when orthogonal cutting AISI 316L’, Int. J.

Mach. Tool. Manu, vol. 47, pp.401-411.

Movahhedy, M.R., Gadala, M.S., and Altintas, Y., 2000.

‘Simulation of the orthogonal metal cutting process

using an arbitrary Lagrangian-Eulerian Finite element

method’, J. Mater. Process. Tech, vol. 103. pp.267-

275.

Kim, K.W., Lee, W.Y., and Sin, H.C., 1999. ‘A finite-

element analysis of machining with the tool edge

considered’, J. Mater. Process. Tech, vol. 86, pp.45-55.

Strenkowski, J.S., Shih, A.J., and Lin, J-C., 2002. ‘An

analytical finite element model for predicting three-

dimensional tool forces and chip flow’, Int. J. Mach.

Tool. Manu, vol. 42, no. 6, pp.723-731.

Nasr, M.N.A., Ng, E-G., and Elbestawi, M.A., 2008. ‘A

modified time-efficient FE approach for predicting

machining-induced residual stresses’, Finite. Elem.

Anal. Des, vol. 44, pp.149-161.

Lennon, A.M. and Ramesh, K.T., 1998. ‘A technique for

measuring the dynamic behaviour of materials at high

temperatures’, Int. J. Plasticity, vol. 14, pp.1279-1292.

Sartkulvanich, P., Koppka, F., and Altan, T., 2004.

‘Determination of flow stress for metal cutting

simulation-a progress report’, J. Mater. Process. Tech,

vol. 146, pp.61-71.

Fu, X.L., 2007. ‘Research on deformation theory and

characteristics of machined surface for high-speed

milling aviation aluminium alloy’, Ph.D dissertation,

Shandong university, JiNan.

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

464