
MULTI-FIDELITY DESIGN OPTIMIZATION OF
AXISYMMETRIC BODIES IN INCOMPRESSIBLE FLOW
Leifur Leifsson, Slawomir Koziel and Stanislav Ogurtsov
Engineering Optimization & Modeling Center, School of Science and Engineering, Reykjavik University
Menntavegur 1, 101 Reykjavik, Iceland
Keywords: Axisymmetric body, Underwater vehicles, Hydrodynamic shape optimization, CFD, Direct design, Inverse
design, Surrogate modelling.
Abstract: The paper discusses multi-fidelity design optimization of axisymmetric bodies in incompressible fluid flow.
The algorithm uses a computationally cheap low-fidelity model to construct a surrogate of an accurate but
CPU-intensive high-fidelity model. The low-fidelity model is based on the same governing equations as the
high-fidelity one, but exploits coarser discretization and relaxed convergence criteria. The low-fidelity model is
corrected by aligning the hull surface pressure and skin friction distributions with the corresponding
distributions of the high-fidelity model using a multiplicative response correction. Our approach can be
implemented in both direct and inverse design approaches. Results of two case studies for hull drag
minimization and target pressure distribution matching show that optimized designs are obtained at
substantially lower computational cost (over 94%) when compared to the direct high-fidelity model
optimization.
1 INTRODUCTION
Autonomous underwater vehicles (AUVs) are
becoming increasingly important in various marine
applications, such as oceanography, pipeline
inspection, and mine counter measures (Yamamoto,
2007). Endurance (speed and range) is one of the
more important attribute of AUVs (Allen et al.,
2000). Vehicle drag reduction and/or an increase in
the propulsion system efficiency will translate to a
longer range for a given speed (or the same distance
in a reduced time). A careful hydrodynamic design
of the AUVs, including the hull shape, the
protrutions, and the propulsion system, is therefore
essential.
The fluid flow around an underwater vehicle with
appendages is characterized by flow features such as
thick boundary layers, vortices and turbulent wakes
generated due to the hull and the appendages (Huang
et al., 1992). These flow features can have adverse
effects on, for example, the performance of the
propulsion system and the control planes. Moreover,
the drag depends highly on the vehicle shape, as
well as on the aforementioned flow features. For that
reason, it is important to account for these effects
during the design of the AUVs.
The prediction of the flow past the full three-
dimensional configuration of the AUVs requires the
use of computational fluid dynamics (CFD).
Numerous applications of CFD methods to the flow
past AUVs and other underwater vehicles are in the
literature, e.g., Yang and Löhner, 2003; Barros et al.
2008; and Jagadeesh et al., 2009. The purpose of
these investigations is to predict properties such as
added masses, pressure and friction distributions,
drag, normal force and moment coefficients, wake
field, and stability derivatives. Comparison with
experimental measurements show that CFD is
reliable and can yield accurate results (Yang and
Löhner, 2003; Barros et al. 2008; and Jagadeesh et
al., 2009).
Numerous studies on underwater vehicle design
and optimization have been reported which focus on
the clean hull only, i.e., the appendages and the
propulsion system are neglected and the flow is
taken to be past an axisymmetric body at a zero
angle of attack. Examples of such numerical studies
include Goldschmied (1966), Parsons et al. (1974),
Myring (1976), Dalton and Zedan (1980), Lutz and
Wagner (1998), Alvarez et al. (2009), and Solov’ev
(2009). Allen et al. (2000), however, report an
465
Leifsson L., Koziel S. and Ogurtsov S..
MULTI-FIDELITY DESIGN OPTIMIZATION OF AXISYMMETRIC BODIES IN INCOMPRESSIBLE FLOW.
DOI: 10.5220/0003646104650473
In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SDDOM-2011), pages
465-473
ISBN: 978-989-8425-78-2
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

experimental investigation of propulsion system
enhancements and drag reduction of an AUV.
The hydrodynamic design optimization of AUVs
in full configuration, taking into account the
appendages and the propulsion system, is still an
open problem. One of the main challenges involved
is the high computational cost of a CFD simulation.
A single CFD simulation of the three-dimensional
flow past an AUV can take a few hours up to several
days, depending on the computational power, the
grid density, and the flow conditions. Therefore, the
direct optimization can be impractial, especially
using traditional gradient-based methods.
An important research area in the field of
aerodynamic optimization is focused on employing
the surrogate-based optimization (SBO) techniques
(Queipo et al., 2005; Forrester and Keane, 2009).
One of the major objectives is to reduce the number
of high-fidelity model evaluations, and thereby
making the optimization process more efficient. In
SBO, the accurate, but computationally expensive,
high-fidelity CFD simulations are replaced—in the
optimization process—by a cheap surrogate model.
SBO has been successfully applied to the
aerodynamic design optimization of various
aerospace components, such as airfoils (e.g.,
Leifsson and Koziel, 2010), aircraft wings (e.g.,
Alexandrov et al., 2000), and turbine blades (e.g.,
Braembussche, 2008).
The surrogate models can be created either by
approximating the sampled high-fidelity model data
using regression (so-called function approximation
surrogates) (see for example Queipo et al., 2005), or
by correcting physics-based low-fidelity models
which are less accurate but computationally cheap
representations of the high-fidelity models (see, e.g.,
Bandler et al., 2004, Alexandrov et al., 2000). The
latter models are typically more expensive to
evaluate. However, less high-fidelity model data is
normally needed to obtain a given accuracy level.
SBO with physics-based low-fidelity models is
called multi- or variable-fidelity optimization.
In this paper, we present a hydrodynamic shape
optimization methodology based on the SBO
concept for AUVs. In particular, we adopt the multi-
fidelity approach with the high-fidelity model based
on the Reynolds-Averaged Navier-Stokes (RANS)
equations, and the low-fidelity model based on the
same equations, but with coarse discretization and
relaxed convergence criteria. We use a simple
response correction to create the surrogate. Here, we
choose to focus on the clean hull design, which is a
convenient case study to implement and test our
design approach.
2 PROBLEM FORMULATION
We constrain the hull shapes to the most common
AUV shape, namely, the torpedo shape, i.e., a three
section axisymmetric body with a nose, a cylindrical
midsection, and a tail. Typically, equipment such as
the computer, sensors, electronics, batteries, and
payload are housed in the nose and the midsection,
whereas the propulsion system is in the tail. Figure 1
shows a typical torpedo shaped hull with a nose of
length a, midsection of length b, overall length L,
and maximum diameter of D.
2.1 Shape Parameterization
We parameterize the nose and the tail using Bézier
curves (Lepine et al., 2001). The Bézier curve, of
degree n, is defined as
∑∑
==
−
−
−
=
m
k
n
i
iin
iPktkt
ini
n
tB
10
)()())(1(
!)(!
!
)(
, (1)
where P
i
, i = 0…n, are the control points, and t is an
1
× m array from 0 to 1.
We use five control points for the nose and four
for the tail, as shown in Fig. 2. Control points
number three and eight are free (x- and y-
coordinates), while the other points are fixed. We,
therefore, have two design variables for the nose and
tail curves, a total of four design variables, aside
from the hull dimensions a, b, L, and D.
Figure 1: A sketch of a typical axisymmetric torpedo
shaped hull form.
2.2 Design Approaches
The goal of hydrodynamic shape optimization is to
find an optimal—with respect to given objectives—
hull shape, so that given design constraints are
satisfied. There are two main approaches two this
problem. One is to adjust the hull geometrical shape
to maximize performance. This is called direct
design, and the most common design goal, when
considering the clean hull, is drag minimization. An
alternative approach is to define a priori a specific
flow behavior that is to be attained. This is called
inverse design, and, typically in hydrodynamic
design, a target velocity distribution is prescribed
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
466
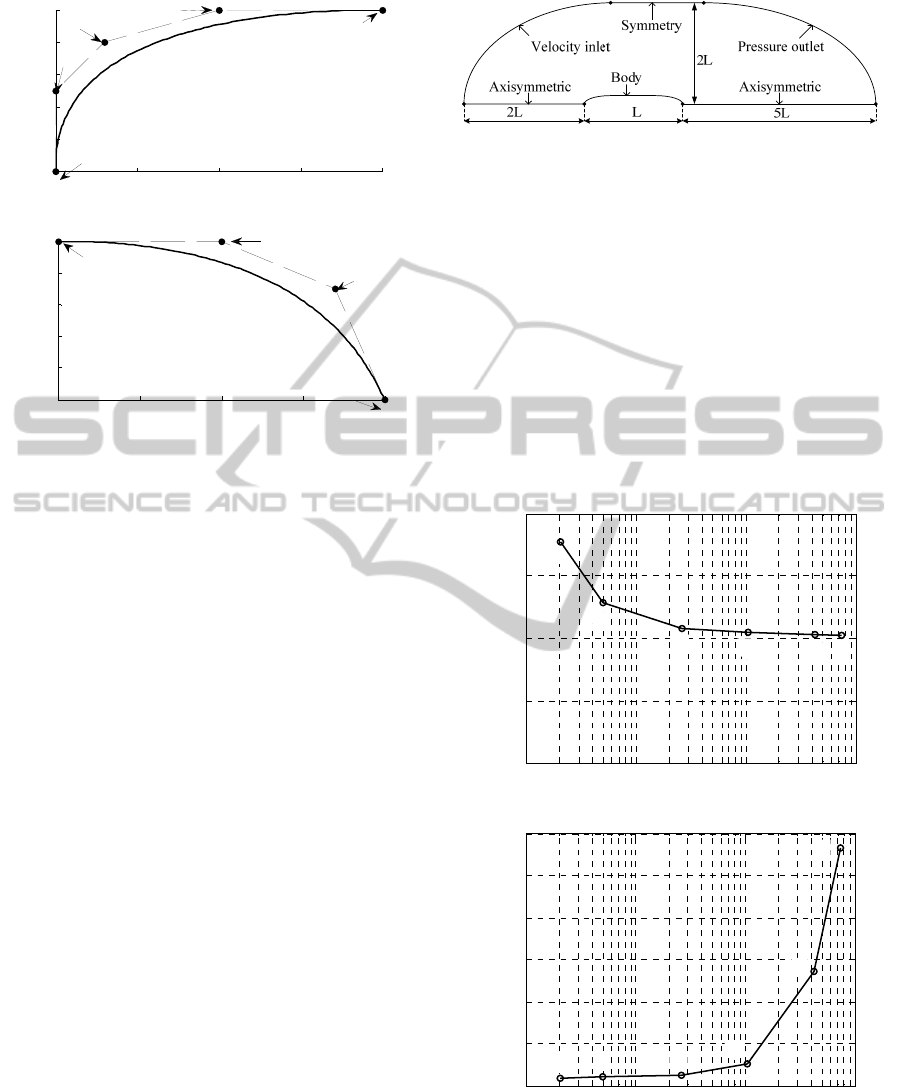
(a)
(b)
Figure 2: Bézier curves are used to represent the shapes of
(a) the nose (5 control points); and (b) the tail (4 control
points). Control points 3 and 8 are free, while the other
points are essentially fixed (depend on L, a, b, and D).
(Dalton and Zedan, 1980). Instead, a target pressure
distribution can be prescribed a priori, which is more
common in aerodynamic design (Dulikravich, 1991).
Typically, inverse design minimizes the norm of the
difference between the target and design
distributions. The main difficulty in this approach is
to define the target distribution. In this paper we
consider both the direct and the inverse design
approaches.
3 COMPUTATIONAL MODELS
3.1 High-Fidelity CFD Model
The flow past the hull is considered to be steady and
incompressible. The Reynolds-Averaged Navier-
Stokes (RANS) equations are assumed as the
governing flow equations with the two-equation k-
ε
turbulence model with standard wall functions
(Tannehill et al., 1997).
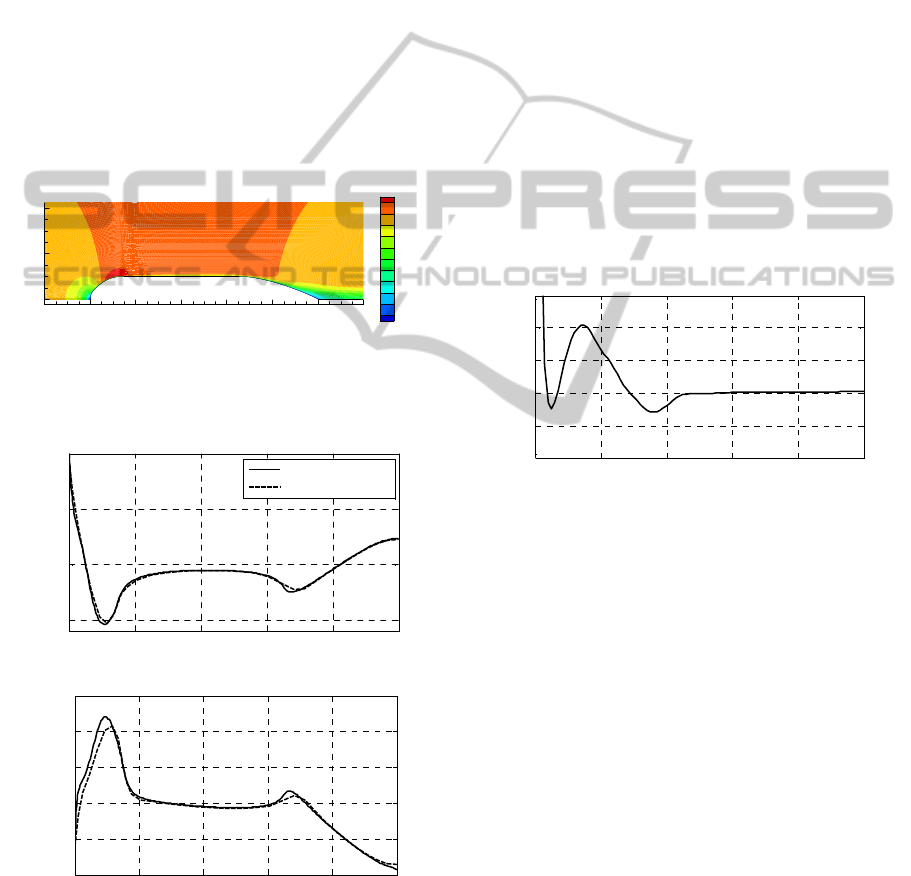
The solution domain is axisymmetric around the
hull centreline axis and extends two body lengths in
front of the hull, five body lengths behind it, and two
body lengths above it (Fig. 3). At the inlet, there is a
velocity boundary condition where the velocity is set
parallel to the hull axis, i.e., zero angle of attack.
Pressure is prescribed at the outlet (zero gauge
pressure).
Figure 3: The computational solution domain and the
boundary conditions.
The CFD computer code FLUENT (2006) is used
for numerical simulations of the fluid flow.
Asymptotic convergence to a steady state solution is
obtained for each case. The iterative convergence of
each solution is examined by monitoring the overall
residual, which is the sum (over all the cells in the
computational domain) of the L
2
norm of all the
governing equations solved in each cell. In addition
to this, the drag force (defined in Section 3.3) is
monitored for convergence. A solution is considered
converged if a residual value of 10
-6
has been
reached for all equations, or the number of iterations
reaches 1000.
(a)
(b)
Figure 4: Grid convergence study at a speed of 2 m/s and
Reynolds number of 2 million; (a) the change in the drag
coefficient C
D
(defined in Section 3.3) with the number of
elements; (b) the variation in the simulation time with
number of elements.
0 0.05 0.1 0.15 0.2
0
0.02
0.04
0.06
0.08
0.1
x/L
r/L
1
2
3
4
5
0.8 0.85 0.9 0.95 1
0
0.02
0.04
0.06
0.08
0.1
x/L
r/L
6
8
9
7
10
2
10
3
10
4
10
5
0
0.05
0.1
0.15
0.2
Number of Elements
C
D
12
3
4
5
6
10
2
10
3
10
4
10
5
0
100
200
300
400
500
600
Number of Elements
Simulation Time [s]
1
2
3
45
6
MULTI-FIDELITY DESIGN OPTIMIZATION OF AXISYMMETRIC BODIES IN INCOMPRESSIBLE FLOW
467
The computational grid is structured with
quadrilateral elements. The elements are clustered
around the body and grow in size with distance from
the body. The grids are generated using ICEM CFD
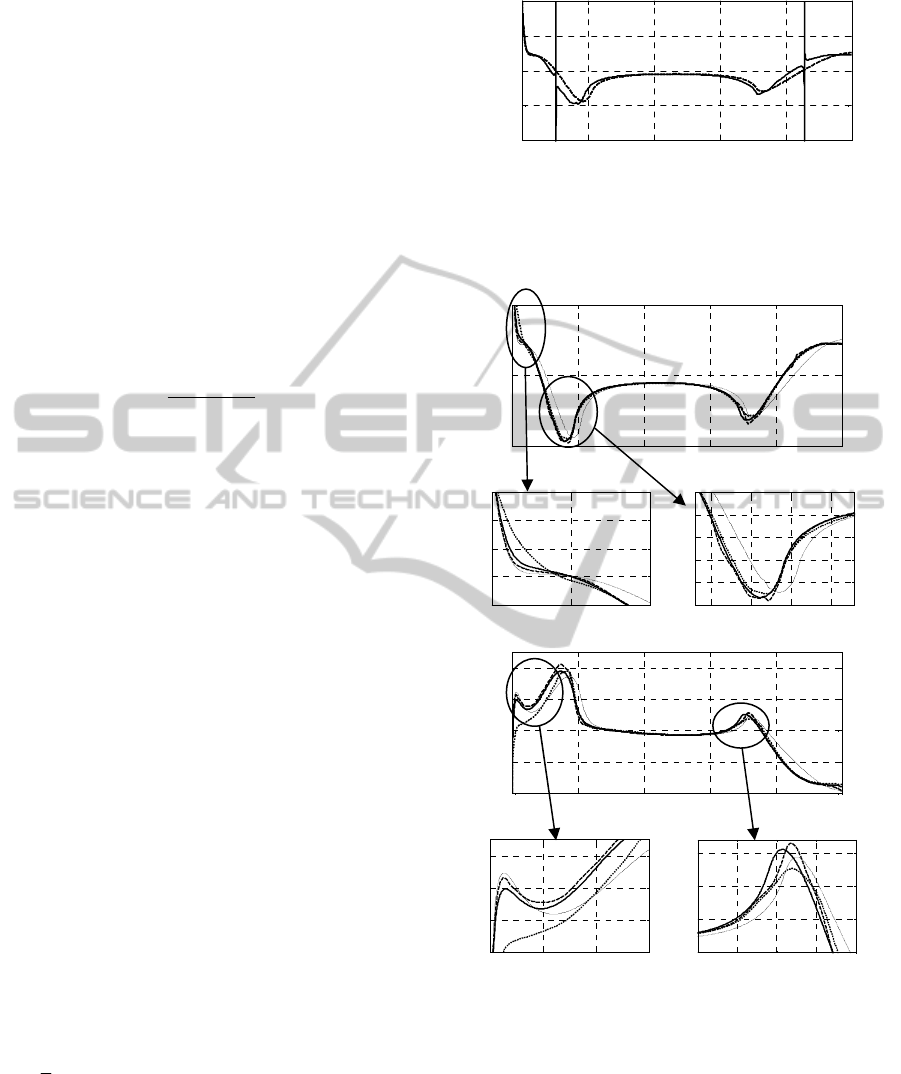
(2006). A grid convergence study was performed to
determine the necessary grid density (Fig. 4). A
torpedo shaped body with L/D = 5 was used in the
study. The inlet speed was 2 m/s and the Reynolds
number was 2 million. Clearly, the drag coefficient
value has converged at the finest grids (number 1
and 2) (Fig. 4(a)). There is, however, a large
difference in the simulation time between the two
finest grids (Fig. 4(b)). Therefore, we selected grid
number 2, with 42,763 elements, to use for the high-
fidelity CFD model in the optimization process.
The velocity contours, pressure and skin friction
distributions are shown in Figs. 5 and 6 for
illustration purposes.
Figure 5: Velocity contours of the flow past an
axisymmetric torpedo shape hull at 2 m/s and Reynolds
number of 2 million. Grid 5 of Fig. 4 was used in the
simulation.
(a)
(b)
Figure 6: Flow distributions (from the high-fidelity and
low-fidelity models (defined in Section 3.2)) on the hull
surface of the flow shown in Fig. 5; (a) the pressure
distribution; and (b) the skin friction distribution.
3.2 Low-Fidelity CFD Model
The low-fidelity model is based on the same CFD
model as the high-fidelity one. However, as the low-
fidelity model will be used in place of the high-
fidelity model in the optimization process, it needs
to be faster than the high-fidelity one. The
simulation time is substantially reduced by making
the grid coarser (Fig. 4(b)). Grid number 6 needs the
lowest simulation time and is the least accurate. A
closer look at that grid reveals that it is too coarse
(the responses were too “grainy”). Consequently, we
selected grid number 5, with 504 elements, to be
used for the low-fidelity model.
The simulation time can be reduced further by
reducing the number of iterations. Figure 7 shows
how the drag coefficient reaches a converged value
after approximately 50 iterations. We therefore relax
the convergence criteria for the low-fidelity model
by setting it to 50 iterations. The ratio of simulation
time of the high-fidelity model to the low-fidelity
model is around 15.
Figure 7: Variation of the drag coefficient with number of
iterations for the case shown in Fig. 5.
3.3 Hull Drag Calculation
For a body in incompressible flow, the total drag is
due to pressure and friction forces, which are
calculated by integrating the pressure (C
p
) and skin
friction (C
f
) distributions over the hull surface. The
pressure coefficient is defined as C
p
≡ (p-p
∞
)/q
∞
,
where p is the local static pressure, p
∞
is free-stream
static pressure, and q
∞
= (1/2
ρ
∞
V
∞
2
) is the dynamic
pressure, with
ρ
∞
as the free-stream density, and the
V
∞
free-stream velocity. The skin friction coefficient
is defined as C
f
≡
τ
/q
∞
, where
τ
is the shear stress.
Typical C
p
and C
f
distributions are shown in Fig. 6.
The total drag coefficient is defined as
C
D
≡ d/(q
∞
S), where d is the total drag force, and S is
the reference area. Here, we use the frontal-area of
the hull as the reference area. The drag coefficient is
the sum of the pressure and friction drag, or
x/L
r/L
-0.2 0 0.2 0.4 0.6 0.8 1 1.2
0
0.2
0.4
2.2
2.0
1.8
1.6
1.4
1.2
1.0
0.8
0.6
0.4
0.2
Velocity [m/s]
0 0.2 0.4 0.6 0.8 1
-0.5
0
0.5
1
C
p
x/L
High-fidelity model
Low-fidelity model
0 0.2 0.4 0.6 0.8 1
0
0.002
0.004
0.006
0.008
0.01
C
f
x/L
0 20 40 60 80 100
0
0.05
0.1
0.15
0.2
0.25
Iterations
C
D
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
468

DfDpD
CCC +=
, (2)
where C
Dp
is the pressure drag coefficient and C
Df
is
the skin friction drag coefficient. The CFD analysis
yields static pressure and wall shear stress values
(which are non-dimensionalized to give C
p
and C
f
) at
the element nodes (Fig. 8). The pressure acts normal
to the surface and the shear stress parallel to it. The
pressure drag coefficient is calculated by integrating
from the leading-edge of the nose to the trailing-
edge of the tail
∫
=
L
pDp
dxxrxxCC
0
)()(sin)(2
θπ
, (3)
where C
p
(x) is assumed to vary linear between the
element nodes,
θ
(x) is angle of each element relative
to the x-axis, and L is the length of the hull.
Similarly, the skin friction drag coefficient is
calculated as
∫
=
L
fDf
dxxrxxCC
0
)()(cos)(2
θπ
. (4)
4 OPTIMIZATION PROCEDURE
4.1 Design Problem Formulation
Our design task is formulated as a nonlinear
minimization problem of the form
*
arg min ( )
f
≤≤
=
lxu
xx
(5)
where f(
x) is the objective function, x is the design
variable vector, whereas
l and u are the lower and
upper bounds, respectively. Here, no nonlinear
constraints are present, the design variables are control
parameters that parameterize the hull shape (cf. Section
2.1). The objective function depends on the particular
design scenario. For direct design (see Section 2.2), the
objective function is just a drag coefficient as defined
in Section 3.3. For inverse design (see Section 2.2), the
objective is defined as a norm of the difference
between the current and the target pressure
distributions.
4.2 Surrogate-based Optimization
The high-fidelity model evaluation is CPU-intensive
so that solving the problem (5) directly, by plugging
in the high-fidelity model into the optimization loop,
may be impractical. Instead, we would like to
exploit surrogate-based optimization (SBO)
(Bandler et al., 2004; Queipo et al., 2005) that shifts
the optimization burden into the computationally
cheap surrogate, and, thus, allows us to solve (5) at a
low computational cost.
Figure 8: Edge of an element on the hull surface at radius
r. The element length is
Δx and it makes an angle
θ
to the
x-axis. Pressure p acts normal to the hull surface. Shear
stress
τ
acts parallel to the surface.
The generic SBO optimization scheme is the
following
(1) ()
arg min ( )
ii
s
+
=
x
xx
(6)
where
x
(i)
, i = 0, 1, ..., is a sequence of approximate
solutions to (5), whereas s
(i)
is the surrogate model at
iteration i. If the surrogate model is sufficiently good
representation of the high-fidelity model f, the
number of iterations required to find a satisfactory
design is small (Koziel et al., 2006).
The surrogate model can be constructed either
from sampled high-fidelity model data using an
appropriate approximation technique (Simpson et
al., 2001), or by utilizing a physically-based low-
fidelity model (Bandler et al., 2004). Here, we
exploit the latter approach as we have a reliable low-
fidelity model at our disposal (see Section 3.2).
Also, good physically-based surrogates can be
constructed using a fraction of high-fidelity model
data necessary to build accurate approximation
models (Koziel and Bandler, 2010a).
There are several methods of constructing the
surrogate from a physically-based low-fidelity
model. They include, among others, space mapping
(SM) (Bandler et al., 2004), various response
correction techniques (Søndergaard, 2003), manifold
mapping (Echeverría and Hemker, 2008), and shape-
preserving response prediction (Koziel, 2010b). In
this paper, the surrogate model is created using a
simple multiplicative response correction, which
turns out to be sufficient for our purposes. An
advantage of such an approach is that the surrogate
is constructed using a single high-fidelity model
evaluation, and it is very easy to implement.
4.3 Surrogate Model Construction
Recall that C
p.f
(x) and C
f.f
(x) denote the pressure and
MULTI-FIDELITY DESIGN OPTIMIZATION OF AXISYMMETRIC BODIES IN INCOMPRESSIBLE FLOW
469
skin friction distributions of the high-fidelity model.
The respective distributions of the low-fidelity model
are denoted as C
p.c
(x) and C
f.c
(x). We will use the
notation C
p.f
(x) = [C
p.f.1
(x) C
p.f.2
(x) ... C
p.f.m
(x)]
T
, where
C
p.f.j
(x) is the jth component of C
p.f
(x), with the
components corresponding to different coordinates
along the x/L axis.
At iteration i, the surrogate model C
p.s
(i)
of the
pressure distribution C
p.f
is constructed using the
multiplicative response correction of the form:
() () () ()
...1..2 ..
( ) [ ( ) ( ) ... ( )]
iii iT
ps ps ps psm
CCC C=xxx x
(7)
() ()
.. . ..
() ()
ii
ps j p j pc j
CAC=⋅xx
(8)
j = 1, 2, ..., m, where
() ()
..
()
.
() ()
..
()
()
ii
pf j
i
pj
ii
pc j
C
A
C
=
x
x
(9)
Similar definition holds for the skin friction
distribution model C
f.s
(i)
. Note that the formulation
(7)-(9) ensures zero-order consistency (Alexandrov
and Lewis, 2001) between the surrogate and the
high-fidelity model, i.e., C
p.f
(x
(i)
) = C
p.s
(i)
(x
(i)
).
Rigorously speaking, this is not sufficient to ensure the
convergence of the surrogate-based scheme (6) to the
optimal solution of (5). However, because of being
constructed from the physically-based low-fidelity
model, the surrogate (7)-(9) exhibits quite good
generalization capability. As demonstrated in Section
5, this is sufficient for good performance of the
surrogate-based design process.
One of the issues of model (7)-(9) is that (9) is not
defined whenever C
p.c.j
(x
(i)
) equals zero, and that the
values of A
p.j
(i)
are very large when C
p.c.j
(x
(i)
) is close to
zero. This may be a source of substantial distortion of
the surrogate model response as illustrated in Fig. 9. In
order to alleviate this problem, the original surrogate
model response is “smoothened” in the vicinity of the
regions where A
p.j
(i)
is large (which indicates the
problems mentioned above). Let j
max
be such that
|A
p.jmax
(i)
| >> 1 assumes (locally) the largest value. Let
Δj be the user-defined index range (typically, Δj =
0.01
⋅m). The original values of A
p.j
(i)
are replaced, for j
= j
max
–Δj, ..., j
max
–1, j
max
, j
max
+1, ..., j
max
+Δj, by the
interpolated values:
max max
max max
()
.max max
max max
() ()
.2 . 1
() ()
.2 . 1
({[ 2 ... 1]
[ 1... 2 ]},
{[ ... ]
[... ]},)
i
pj
ii
pj j pj j
ii
pj j pj j
AIj jj j
jjj j
AA
AA j
−Δ −Δ−
−Δ −Δ−
=−Δ−Δ−∪
∪+Δ− +Δ
∪
∪
(10)
Figure 9: Surrogate model C
p.s
(i)
(7)-(9) at x
(i)
(- - -), and at
some other design
x (▬). By definition, C
p.s
(i)
(x
(i)
) =
C
p.f
(x
(i)
). Note that C
p.s
(i)
(x) has large spikes around the
points where C
p.s
(i)
(x
(i)
) is close to zero.
(a)
(b)
Figure 10: (a) Smoothened surrogate model (7)-(10)
C
p.s
(i)
(x
(i)
) = C
p.f
(x
(i)
) (—), C
p.s
(i)
(x) (- - -), C
p.c
(x) (⋅ ⋅ ⋅), and
C
p.s
(x) (▬); (b) Smoothened responses C
f.s
(i)
(x
(i)
) = C
f.f
(x
(i)
)
(—), C
f.s
(i)
(x) (- - -), C
f.c
(x) (⋅ ⋅ ⋅), and C
f.s
(x) (▬).
where I(X,Y,Z) is a function that interpolates the
function values Y defined over the domain X onto
the set Z. Here, we use cubic splines. In other words,
the values of A
p.j
(i)
in the neighbourhood of j
max
are
“restored” using the values of A
p.j
(i)
from the
surrounding of j = j
max
–Δj, ..., j
max
+Δj.
0 0.2 0.4 0.6 0.8 1
-1
-0.5
0
0.5
1
x/L
C
p
0 0.2 0.4 0.6 0.8 1
-0.5
0
0.5
x/L
C
f
0 0.05 0.1
0
0.2
0.4
0.6
0.8
0.1 0.15 0.2 0.25
-0.5
-0.4
-0.3
-0.2
-0.1
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
x/L
C
f
0 0.05 0.1 0.15
0.4
0.5
0.6
0.7
0.6 0.65 0.7 0.75 0.8
0.35
0.4
0.45
0.5
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
470
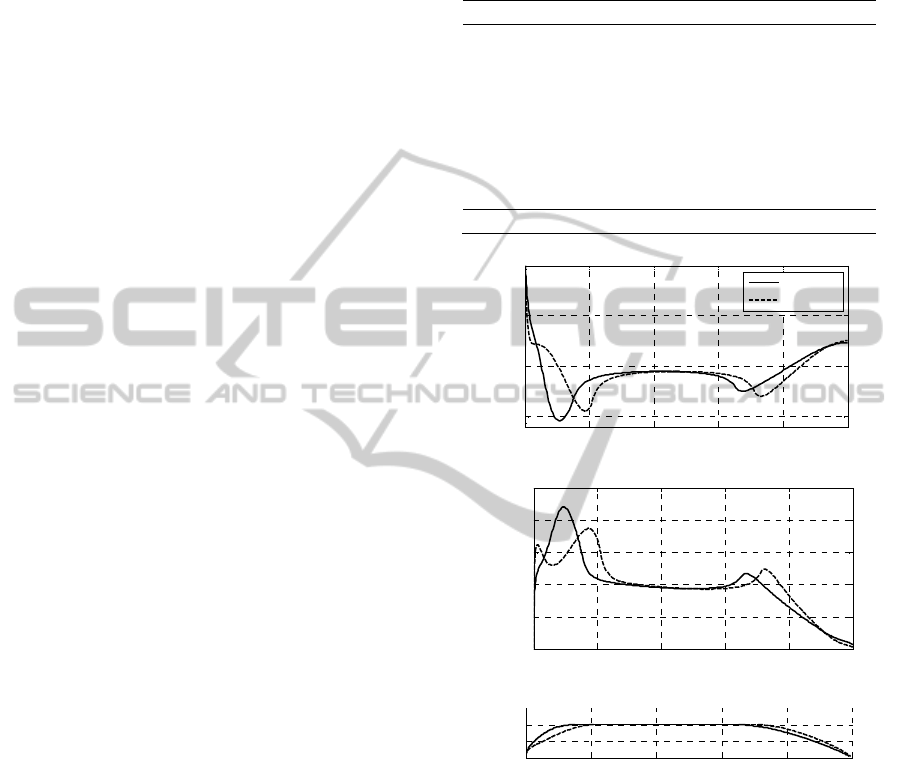
Figure 10(a) shows the “smoothened” surrogate
model response corresponding to that of Fig. 9.
Figure 10 shows the surrogate and the high-fidelity
model responses, both C
p
and C
f
, at x
(i)
and at some
other design
x.
5 NUMERICAL EXAMPLES
5.1 General Setup
The proposed approach is applied to the
hydrodynamic shape optimization of torpedo-type
hulls, involving both the direct and inverse design
approaches. Designs are obtained using the
algorithm proposed in Section 4, where the surrogate
model optimization is performed using the pattern-
search algorithm
(Koziel, 2010c). For comparison
purposes, designs obtained through direct
optimization of the high-fidelity model using the
pattern-search algorithm
(Koziel, 2010c) are also
presented.
For both the direct and the inverse design
approaches, the design variable vector is
x = [a x
n
y
n
x
t
y
t
]
T
, where a is the nose length, (x
n
,y
n
) and (x
t
,y
t
)
are the coordinates of the free control points on the
nose and tail Bézier curves, respectively, i.e., points
3 and 8 in Fig. 2. See Section 2.1 for a description of
the shape parameterization. The lower and upper
bounds of design variables are
l = [0 0 0 80 0]
T
cm
and
u = [30 30 10 100 10]
T
cm, respectively. Other
geometrical shape parameters are, for both cases, L
= 100 cm, d = 20 cm, and b = 50 cm. The flow speed
is 2 m/s and the Reynolds number is 2 million.
5.2 Direct Design
Numerical results for a direct design case are
presented in Table 1. The hull drag coefficient is
minimized by finding the appropriate shape and
length of the nose and tail sections for a given hull
length, diameter, and cylindrical section length. In
this case, the drag coefficient is reduced by 6.3%.
This drag reduction comes from a reduction in skin
friction and a lower pressure peak where the nose
and tail connect with the midsection (Figs. 11(a) and
11(b)). These changes are due to a more streamlined
nose (longer by 6 cm) and a fuller tail, when
compared to the initial design (Fig. 11(c)).
Table 1: Numerical results for direct drag minimization.
The flow speed is 2 m/s and the Reynolds number is 2
×
10
6
. All the numerical values are from the high-fidelity
model. N
c
and N
f
are the number of low- and high-fidelity
model evaluations, respectively.
Variable Initial Pattern-search This work
a 15.0000 21.8611 20.9945
x
n
5.0000 5.6758 5.6676
y
n
5.0000 2.7022 2.7531
x
t
90.0000 98.000 96.6701
y
t
5.0000 0.8214 3.0290
C
D
0.0915 0.0853 0.0857
N
c
N/A 0 300
N
f
N/A 282 3
Total cost N/A 282 13
(a)
(b)
(c)
Figure 11: Direct hull drag minimization results showing
initial and optimized (a) pressure distributions; (b) skin
friction distributions; and (c) hull shapes.
The proposed method requires 3 high-fidelity and
300 low-fidelity model evaluations. The ratio of the
high-fidelity model evaluation time to the corrected
low-fidelity model evaluation time varies between
11 to 45, depending on whether the flow solver
converges to the residual limit of 10
-6
, or the
maximum iteration limit of 1000. We express the
total optimization cost of the proposed method in the
equivalent number of high-fidelity model
evaluations. For the sake of simplicity, we use a
0 0.2 0.4 0.6 0.8 1
-0.5
0
0.5
1
x/L
C
p
Initial
Optimized
0 0.2 0.4 0.6 0.8 1
0
0.002
0.004
0.006
0.008
0.01
x/L
C
f
0 0.2 0.4 0.6 0.8 1
0
0.05
0.1
x
/L
r/L
MULTI-FIDELITY DESIGN OPTIMIZATION OF AXISYMMETRIC BODIES IN INCOMPRESSIBLE FLOW
471

fixed value of 30 as the high- to low-fidelity model
evaluation time ratio. The results show that the total
optimization cost of the proposed method is around
13 equivalent high-fidelity model evaluations. The
direct optimization method, using the pattern-search
algorithm (Koziel, 2010c), yields very similar
design, but at the substantially higher computational
cost of 282 high-fidelity model evaluations.
5.3 Inverse Design
Inverse design of the hull shape was performed by
prescribing a target pressure distribution. The
objective is to minimize the norm of the difference
between the pressure distribution of the hull design
and the target pressure distribution. The design
variables and constraints are shown in Section 5.1.
The numerical results are of the inverse design
are presented in Table 2. The proposed algorithm
matched the target pressure distribution (the norm of
the distributions is less than 2
× 10
-5
) using less than
22 equivalent high-fidelity model evaluations. The
direct optimization of the high-fidelity model using
the pattern-search algorithm required 401 function
calls to yield a comparable matching with the target.
Table 2: Numerical results for inverse design optimization
with a target pressure distribution. N
c
and N
f
are the
number of low- and high-fidelity model evaluations,
respectively. F is the norm of the difference between the
target and the design shapes.
Variable Initial Pattern-search This work
A 18.000 24.7407 24.7667
x
n
7.0000 7.3704 6.8333
y
n
8.0000 4.7407 4.5667
x
t
85.0000 88.1111 88.6333
y
t
7.0000 5.5926 5.3000
F 0.0204 1.64E-5 1.93E-5
C
D
0.0925 0.0894 0.0893
N
c
N/A 0 500
N
f
N/A 401 5
Total cost N/A 401 < 22
6 CONCLUSIONS
Computationally efficient simulation-driven multi-
fidelity design optimization algorithm for
axisymmetric hulls in incompressible fluid flow is
presented. Our algorithm exploits a low-fidelity
model, obtained through a coarse-discretization CFD
simulation, and a response correction method, to
construct a cheap and reliable surrogate of the fluid
(a)
(b)
Figure 12: Results of the inverse design optimization with
a prescribed target pressure distribution; (a) the target,
initial, and optimized pressure distributions; (b) initial and
optimized hull shapes.
flow. The algorithm can be applied to both direct
and inverse design approaches. We demonstrate that
the optimized designs can be obtained at a low
computational cost corresponding to a few high-
fidelity CFD simulations.
REFERENCES
Allen, B., Vorus, W. S., and Prestero, T., 2000, Propulsion
system performance enhancements on REMUS AUVs,
In Proceedings MTS/IEEE Oceans 2000, September,
Providence, Rhode Island.
Alexandrov, N. M., Lewis, R. M., Gumbert, C.R., Green,
L. L., and Newman, P.A., 2000, Optimization with
variable-fidelity models applied to wing design, 38
th
Aerospace Sciences Meeting & Exhibit, Reno, NV,
AIAA Paper 2000-0841.
Alexandrov, N. M., Lewis, R. M., 2001, An overview of
first-order model management for engineering
optimization. Optimization and Engineering. 2, 413-
430.
Alvarez, A., Bertram, V., and Gualdesi, L., 2009, Hull
hydrodynamic optimization of autonomous
underwater vehicles operating at snorkelling depth,
Ocean Engineering, vol. 36, pp. 105-112.
Bandler, J. W., Cheng, Q. S., Dakroury, S. A., Mohamed,
A. S., Bakr, M.H., Madsen, K., and Søndergaard, J.,
2004, Space Mapping: The State of The Art. IEEE
Trans. Microwave Theory Tech., 52(1), pp. 337-361.
0 0.2 0.4 0.6 0.8 1
-0.5
0
0.5
1
x/L
C
p
Target
Initial
Optimized
0.15 0.2 0.25 0.3
-0.4
-0.3
-0.2
-0.1
0.7 0.75 0.8 0.85
-0.4
-0.3
-0.2
-0.1
0 0.2 0.4 0.6 0.8 1
0
0.05
0.1
x
/L
r/L
SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and
Applications
472

Braembussche, R. A., 2008, Numerical Optimization for
Advanced Turbomachinery Design, In Optimization
and Computational Fluid Dynamics, Thevenin, D. and
Janiga, G., editors, Springer, pp. 147-189.
Dalton, C., and Zedan, M. F., 1980, Design of low-drag
axisymmetric shapes by the inverse method, J.
Hydronautics, vol. 15, no. 1, pp. 48-54.
Dulikravich, G. S., 1991, Aerodynamic shape design and
optimization, 29
th
AIAA Aerospace Sciences Meeting,
Reno, NV.
de Barros, E. A., Dantas, J. L. D., Pascoal, A. M., and de
Sá, E., 2008, Investigation of normal force and
moment coefficients for an auv at nonlinear angle of
attack and sideslip angle, IEEE Journal of Oceanic
Engineering, vol. 33, no. 4, pp. 538-549.
Echeverría, D., and Hemker, P.W., 2008, Manifold
mapping: a two-level optimization technique.
Computing and Visualization in Science. 11, pp. 193-
206.
FLUENT, ver. 12.1, ANSYS Inc., Southpointe, 275
Technology Drive, Canonsburg, PA 15317, 2006.
Forrester, A.I.J., and Keane, A.J., 2009, Recent advances
in surrogate-based optimization, Progress in
Aerospace Sciences, vol. 45, no. 1-3, pp. 50-79.
Goldschmied, F.R., 1966, Integrated hull design,
boundary-layer control, and propulsion of submerged
bodies, J. Hydronautics, vol. 1, no. 1, pp. 2-11.
Huang, T. T., Liu, H. L., Groves, N. C., Forlini, T. J.,
Blanton, J. N., and Gowing, S., 1992, Measurements
of flows over an axisymmetric body with various
appendages (DARPA SUBOFF Experiments), In
Proceedings of the 19
th
Symposium on Naval
Hydrodynamics, Seoul, Korea.
ICEM CFD, ver. 12.1, ANSYS Inc., Southpointe, 275
Technology Drive, Canonsburg, PA 15317, 2006.
Jagadeesh, P., Murali, K., Idichandy, V.G., 2009,
Experimental investigation of hydrodynamic force
coefficients over auv hull form, Ocean Engineering,
vol. 36, pp. 113-118.
Koziel, S., Bandler, J.W., and Madsen, K., 2006, A Space
Mapping Framework for Engineering Optimization:
Theory and Implementation. IEEE Trans. Microwave
Theory Tech., 54(10), pp. 3721-3730.
Koziel, S., and Bandler, J.W., 2010a, Recent advances in
space-mapping-based modeling of microwave devices.
International Journal of Numerical Modelling, (23) 6,
pp. 425-446
Koziel, S., 2010b, Shape-preserving response prediction
for microwave design optimization. IEEE Trans.
Microwave Theory and Tech., 58(11), pp. 2829-2837.
Koziel, S., 2010c, Multi-fidelity multi-grid design
optimization of planar microwave structures with
Sonnet, International Review of Progress in Applied
Computational Electromagnetics, Tampere, Finland,
April 26-29, pp. 719-724.
Leifsson, L., and Koziel, S., 2010, Multi-fidelity design
optimization of transonic airfoils using physics-based
surrogate modeling and shape-preserving response
prediction, Journal of Computational Science, vol. 1,
no. 2, pp. 98-106.
Lepine, J., Guibault, F., Trepanier, J.-Y., and Pepin, F.,
2001, Optimized nonuniform rational b-spline
geometrical representation for aerodynamic design of
wings, AIAA Journal, vol. 39, no. 11, pp. 2033-2041.
Lutz, Th., and Wagner, S., 1998, Numerical shape
optimization of natural laminar flow bodies, In
Proceedings of the 21st ICAS Congress, Sept. 13-18,
Melbourne, Australia.
Myring, D.F., 1976, A theoretical study of body drag in
subcritical axisymmetric flow, Aeronautical
Quarterly, vol. 28, pp. 186-194.
Parsons, J.S., Goodson, R.E., and Goldschmied, F.R.,
1974, Shaping of axisymmetric bodies for minimum
drag in incompressible flow, J. Hydronautics, vol. 8,
no. 3, pp. 100-107.
Queipo, N. V., Haftka, R. T., Shyy, W., Goel, T.,
Vaidynathan, R., and Tucker, P.K., 2005, Surrogate-
Based Analysis and Optimization. Progress in
Aerospace Sciences, 41(1), pp. 1-28.
Simpson, T. W., Peplinski, J., Koch, P.N., Allen, J.K.,
2001, Metamodels for computer-based engineering
design: survey and recommendations. Engineering
with Computers. 17, pp. 129-150.
Solov’ev, S. A., 2009, Determining the shape of an
axisymmetric body in a viscous incompressible flow
on the basis of the pressure distribution on the body
surface, J. of Applied Mechanics and Technical
Physics, vol. 50, no. 6, pp. 927-935.
Søndergaard, J., 2003, Optimization using surrogate
models – by the space mapping technique. Ph.D.
Thesis, Informatics and Mathematical Modelling,
Technical University of Denmark, Lyngby.
Tannehill, J.A., Anderson, D.A., and Pletcher, R.H., 1997,
Computational fluid mechanics and heat transfer, 2
nd
edition, Taylor & Francis.
Yang, C., and Löhener, R., 2003, Prediction of flows over
an axisymmetric body with appendages, The 8
th
International Conference on Numerical Ship
Hydrodynamics, Sept. 22-25, Busan, Korea.
Yamamoto, I., 2007, Research and development of past,
present, and future auv technologies, in Proc. Int.
Mater-class AUV Technol. Polar Sci. – Soc.
Underwater Technol., Mar. 28-29, pp.17-26.
MULTI-FIDELITY DESIGN OPTIMIZATION OF AXISYMMETRIC BODIES IN INCOMPRESSIBLE FLOW
473
