TRANSONIC AIRFOIL DESIGN BY THE INVERSE METHOD

USING VARIABLE-FIDELITY MODELLING

Slawomir Koziel, Leifur Leifsson and Stanislav Ogurtsov

Engineering Optimization & Modeling Center, School of Science and Engineering

Reykjavik University, Menntavegur 1, Reykjavik, Iceland

Keywords: Inverse airfoil design, Target pressure distribution, Surrogate models, Variable-resolution modelling,

Response surface modelling.

Abstract: The paper presents an improved optimization algorithm for the inverse design of transonic airfoils. Our

approach replaces the direct optimization of an accurate, but computationally expensive, high-fidelity airfoil

model by an iterative re-optimization of two different surrogate models. Initially, for a few design iterations,

a corrected physics-based low-fidelity model is employed, which is subsequently replaced by a response

surface approximation model. The low-fidelity model is based on the same governing fluid flow equations

as the high-fidelity one, but uses coarser discretization and relaxed convergence criteria. A shape-preserving

response prediction technique is utilized to align the pressure distribution of the low-fidelity model with that

of the high-fidelity one. This alignment process is particularly suitable since the inverse design aims at

matching a given target pressure distribution. Our algorithm is applied to constrained inverse airfoil design

in inviscid transonic flow. A comparison with the basic version of the optimization algorithm, exploiting

only a physics-based low-fidelity model, is also carried out. While the performance of both versions is

similar with respect to their ability to match the target pressure distribution, the improved algorithm offers

substantial design cost savings, from 25 to 72 percent, depending on the test case.

1 INTRODUCTION

Aerodynamic shape optimization (ASO) involves

the design of aerodynamic components such as

aircraft wings and turbine blades (Leoviriyakit et al.,

2003); (Braembussche, 2008). The state-of-the-art

ASO design methods employ high-fidelity

computational fluid dynamic (CFD) simulations as a

part of efficient numerical optimization algorithms

(Queipo et al., 2005); (Forrester and Keane, 2009);

(Alexandrov et al., 2000); (Robinson et al., 2008).

The accurate CFD simulations typically lead to more

realistic and attainable designs. The downside is that

the high-fidelity CFD analysis is computationally

expensive and design optimization normally requires

a large number of simulations, which leads to a time

consuming design process.

The introduction of surrogate-based optimization

(SBO) methods (Queipo et al., 2005); (Forrester and

Keane, 2009) to ASO permitted reduction of the

overall computational cost, as well as handling noisy

objective functions. Examples of such work can be

found in the literature (see e.g., Alexandrov et al.,

2000); Robinson et al., 2008); (Booker et al., 1999);

(Barrett et al., 2006); (Leifsson and Koziel, 2010);

(Lane and Marshall, 2010).

A computationally efficient design optimization

methodology for the inverse ASO of transonic

airfoils was recently introduced (Leifsson and

Koziel, 2011). The approach replaces the direct

optimization of an accurate, but computationally

expensive, high-fidelity airfoil model by an iterative

re-optimization of a corrected low-fidelity model.

The low-fidelity model is based on the same

governing fluid flow equations as the high-fidelity

one, but uses coarser discretization and relaxed

convergence criteria. The shape-preserving response

prediction technique (Koziel, 2010a) is utilized to

align the pressure distribution of the low-fidelity

model with that of the high-fidelity model. This

alignment process is particularly suitable since a

target pressure distribution is specified in the inverse

design problem.

In this work, we substantially enhance the

optimization methodology introduced in Leifsson

and Koziel (2011). More specifically, the low-

474

Koziel S., Leifsson L. and Ogurtsov S..

TRANSONIC AIRFOIL DESIGN BY THE INVERSE METHOD USING VARIABLE-FIDELITY MODELLING.

DOI: 10.5220/0003646204740482

In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SDDOM-2011), pages

474-482

ISBN: 978-989-8425-78-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

fidelity CFD model is replaced - after a few design

iterations - by its (local) response surface

approximation, which allows us to reduce the overall

design cost and obtain faster convergence when

compared to the original version of the algorithm.

Our approach is demonstrated using several

transonic airfoil design cases.

2 PROBLEM FORMULATION

The airfoil shape optimization can be formulated as

a constrained nonlinear minimization problem. For a

given set of operating conditions, solve

;;,,1,0)(

;,,1 ,0)(s.t.)( min

uxlx





Nkh

Mjgf



(1)

where f(x) is the objective function, x is the design

variable vector, g

(x) are the inequality constraints,

M is the number of the inequality constraints, h

(x)

are the equality constraints, N is the number of the

equality constraints, and l and u are the design

variables lower and upper bounds, respectively.

There are two main approaches to airfoil design.

One is to directly adjust the geometry parameters of

the airfoil section in order to maximize its

performance. This is called direct design, and the

most common formulations include lift

maximization, drag minimization, and lift-to-drag

ratio maximization (Leifsson and Kozel, 2010).

Another way is to define a priori a specific flow

behavior that is to be attained. The airfoil shape is

then designed to achieve this flow behavior. This is

called inverse design (Dulikravich, 1991).

In inverse design, the role of the designer is to

specify a particular flow feature, which typically is a

target pressure distribution, C

p.t

, on the surface of the

airfoil. The task is then to find the airfoil shape that

can give the target pressure distribution at the

desired flow condition. This can be done by

minimizing the difference between the pressure

distribution of the airfoil C

and the target

distribution C

p.t

The objective function can be formulated as the L

norm of the difference between the airfoil pressure

distribution and the target pressure distribution, or f(x)

= ½ [C

(x) - C

p.t

]

ds. A minimum thickness is

normally specified so that the optimizer does not

reduce the airfoil to a thin plate. The thickness

constraint can be written as g(x) = A

min

– A(x) ≤ 0,

where A(x) is the cross-sectional area of the airfoil

and A

min

is the minimum cross-sectional area.

In this paper, we use the NACA airfoil shapes. In

particular, we use the NACA four-digit airfoil

parameterization method, where the airfoil shape is

defined by three parameters m (the maximum

ordinate of the mean camberline as a fraction of

chord), p (the chordwise position of the maximum

ordinate) and t/c (the thickness-to-chord ratio). The

airfoils are denoted by NACA mpxx, where xx

represents the value of t/c. The shapes are

constructed using two polynomials, one for the

thickness distribution and the other for the mean

camber line. The full details of the NACA four-digit

parameterization method are given in Abbott and

Doenhoff (1959). Three example NACA four-digit

airfoils are shown in Fig. 1.

3 CFD MODELLING

A single CFD simulation is, in general, composed of

four steps; the geometry generation (described here

in Section 2), meshing of the solution domain,

numerical solution of the governing fluid flow

equations, and post-processing of the flow results,

which involves, in the case of numerical

optimization, calculating the objectives and

constraints. In this section we present the high- and

low-fidelity CFD models.

3.1 High-fidelity CFD Model

The flow is assumed to be steady, inviscid, and

adiabatic with no body forces. The Euler equations

are taken to be the governing fluid flow equations

(Tannehill et al., 1997). The computational meshes

used in this study are all of structured curvilinear

body-fitted C-topology.

Figure 1: Shown are three different NACA four-digit

airfoil sections; NACA 0012 (m = 0, p = 0, t/c = 0.12)

solid line (-), NACA 2412 (m = 0.02, p = 0.4, t/c = 0.12)

dashed line (--), NACA 4608 (m = 0.04, p = 0.6, t/c =

0.08) dash-dot line (--).

The solution domain boundaries are placed at 24

chord lengths in front of the airfoil, 50 chord lengths

behind it, and 25 chord lengths above and below it.

The meshes are generated with the computer code

ICEM CFD (2006). A fine mesh was developed with

a total of 320 points in the vertical direction, 180

points on the airfoil surface and 160 points in the

0 0.2 0.4 0.6 0.8 1

-0.1

0.1

NACA 0012

NACA 2412

NACA 4608

TRANSONIC AIRFOIL DESIGN BY THE INVERSE METHOD USING VARIABLE-FIDELITY MODELLING

475

wake behind the airfoil, with a total of 106 thousand

cells. An example computational mesh is shown in

Fig. 2.

The numerical fluid flow simulations are

performed using the computer code FLUENT

(2006). Asymptotic convergence to a steady state

solution is obtained for each case. The iterative

convergence of each solution is examined by

monitoring the overall residual, which is the sum

(over all the cells in the computational domain) of

the L

norm of all the governing equations solved in

each cell. In addition to this, the lift and drag forces

(defined in Section 3.3) are monitored for

convergence. The criteria used in this work for the

high-fidelity model is a maximum residual of 10

-6

or a maximum number of iterations of 1000.

(a)

(b)

Figure 2: (a) An example computational mesh with a

structured C-topology for a NACA 0012 airfoil; (b) a view

close to the airfoil surface.

3.2 Low-fidelity CFD Model

The low-fidelity CFD model is constructed using the

high-fidelity model, but with a coarser

computational mesh and relaxed convergence

criteria. The parameters of the mesh and the number

of solver iterations were obtained by performing a

parametric study using the NACA 2412 airfoil

section at M



= 0.75 and α = 1 deg.

Initially the fine mesh is solved to full

convergence. The solver needed 216 iterations to

reach a converged solution based on the residuals of

the governing equations. However, the lift and drag

coefficient values reached a converged value after

approximately 50 iterations. Therefore, the number

of iterations limit was set to 100 hundred iterations

in the subsequent steps.

The mesh points were reduced in two steps. First,

the number of mesh points in the z-direction and the

number of mesh points behind the airfoil were

reduced by (approximately) half. This procedure was

repeated and in each step the pressure distribution

was plotted. It was observed that the shock location

moved rearward. After five subsequent steps, the

pressure distribution became highly distorted near

the leading-edge. The previous mesh was then

retained and the number of mesh points on the airfoil

surface was reduced incrementally. Again, the

pressure distribution was plotted for each step. It

was observed that the shock strength reduced in each

step as the mesh got coarser and coarser on the

airfoil surface. After three steps the procedure was

halted. The resulting mesh has 48 points in the z-

direction, 115 points on the airfoil surface, and 20

points in the wake behind the airfoil, with a total of

8295 thousand cells. The overall evaluation time is

reduced to about 34 s, which is approximately 13.5

times faster than the high-fidelity model using the

fine mesh and traditional convergence criteria.

The overall evaluation time of the high-fidelity

model in this parametric study is 471 s with a total

of 216 iterations. In many cases the solver does not

fully converge with respect to the residuals and goes

on up to 1000 iterations. Then the overall evaluation

time goes up to 2500 s, and the low-fidelity model is

approximately 73 times faster. For the sake of

simplicity, we will use a fixed value of 50 in the

numerical computations presented later in the paper.

3.3 Aerodynamic Forces

The non-dimensional force coefficients parallel to

the x- and z-axes, C

and C

, respectively, are

calculated by integrating the pressure distribution C

over the surface of the airfoil as (Tannehill et al.,

1997)



 dsCC



sin



 dsCC



cos

(2)

where ds is the surface panel element of length and



is the angle the panel makes relative to the x-axis.

The lift coefficient C

and the wave drag coefficient

are calculated as



cossin

zxl

CCC









sincos

zxdw

CCC





(3)

x/c

z/c

-20 0 20 40

-20

-10

x/c

z/c

0 0.2 0.4 0.6 0.8 1

-0.4

-0.2

0.2

0.4

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

476

4 SURROGATE MODELING

In order to use the low-fidelity model as a reliable

prediction tool in the optimization process, it has to

be corrected to become a reliable representation of

the high-fidelity model. The corrected low-fidelity

model is called a surrogate. The surrogate model can

replace the high-fidelity one in the optimization

process and thus reduce the overall optimization

cost.

Here, we adopt a shape-preserving response

prediction (SPRP) methodology introduced in

(Koziel, 2010a) in the context of microwave

engineering, and recently applied for direct airfoil

design (Leifsson and Koziel, 2010). SPRP is easy to

implement, unlike space mapping it does not need

any auxiliary transformations or extractable

parameters (Koziel et al., 2008). Also, it does not

require high-fidelity model derivative information.

By formulation, SPRP works directly with the

model outputs that can be described by certain

number of design-variable-dependent characteristic

features (Koziel, 2010a). In the case of a pressure

distribution, these features may include the location

and strength of the shock, the pressure at the

leading- and trailing-edges, and many others. In

direct airfoil design, the pressure distribution is an

intermediate simulation result, with the figures of

interest, such as lift or wave drag, being derived

from it. In inverse design, the pressure distribution is

the main object of interest, which makes SPRP well

suited for this kind of problem.

We will denote the vector of design variables as

x. The pressure distribution for the high- and low-

fidelity models will be denoted as C

p.f

and C

p.c

respectively. The surrogate model is constructed

assuming that the change of C

p.f

due to the

adjustment of the design variables x can be predicted

using the actual changes of C

p.c

. The change of C

p.c

is described by the translation vectors corresponding

to certain (finite) number of its characteristic points.

These translation vectors are subsequently used to

predict the change of C

p.f

, whereas the actual C

p.f

the current design, C

p.f

(i)

), is treated as a reference.

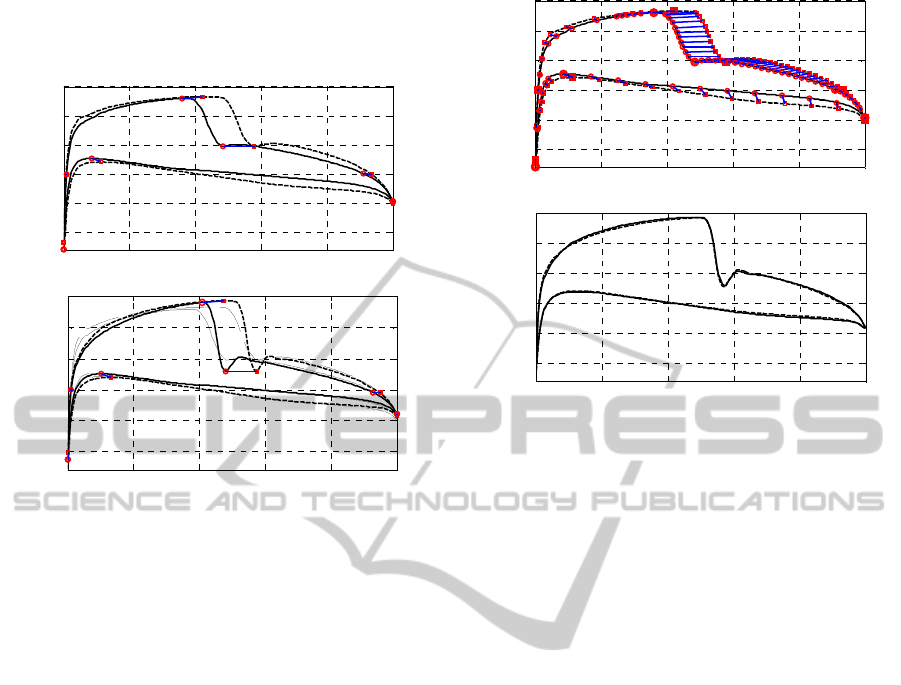
Figure 3(a) shows the pressure distribution C

p.c

of the low-fidelity model at x

(i)

= [0.02 0.4 0.12]

(NACA 2412 airfoil) for M



= 0.7 and α = 1 deg, as

well as C

p.c

at x = [0.025 0.56 0.122]

; x

(i)

will

denote a current design (at the ith iteration of the

optimization algorithm; the initial design will be

denoted as x

(0)

accordingly). Circles denote

characteristic points of C

p.c

(i)

), here, representing,

among others, x/c equal to 0 and 1 (leading and

trailing airfoil edges, respectively), the maxima of

p.c

for the lower and upper airfoil surfaces, as well

as the local minimum of C

p.c

for the upper surface.

The last two points are useful to locate the pressure

shock. Squares denote corresponding characteristic

points for C

p.c

(x), while small line segments

represent the translation vectors that determine the

“shift” of the characteristic points of C

p.c

when

changing the design variables from x

(i)

to x.

In order to obtain a reliable prediction, the

number of characteristic points has to be larger than

illustrated in Fig. 3(a). Additional points are inserted

in between initial points either uniformly with

respect to x/c (for those parts of the pressure

distribution that are almost flat) or based on the

relative pressure value with respect to corresponding

initial points (for those parts of the pressure

distribution that are “steep”). Figure 3(b) shows the

full set of characteristic points (initial points are

distinguished using larger markers).

The pressure distribution of the high-fidelity

model at the given design, here, x, can be predicted

using the translation vectors applied to the

corresponding characteristic points of the pressure

distribution of the high-fidelity model at x

(i)

p.f

(i)

). This is illustrated in Figure 4(a) where only

initial characteristic points and translation vectors

are shown for clarity. Figure 4(b) shows the

predicted pressure distribution of the high-fidelity

model at x as well as the actual C

p.f

(x). The

agreement between both curves is very good.

Rigorous formulation of the SPRP technique can

be found in Koziel (2010a). We omit the details here

for the sake of brevity. It should be mentioned that

the SPRP model assumes that the high- and low-

fidelity model pressure distributions have

corresponding sets of characteristic points. This is

usually the case for the practical ranges of design

variables because the overall shape of the

distributions is similar for both models. In case of a

lack of correspondence, original definitions of

characteristic points are replaced by their closest

counterparts. The typical example would be non-

existence of the local minimum of the pressure

distribution for the upper surface for the high- and/or

low-fidelity model at certain designs. In this case,

the original point (local minimum) is replaced by the

points characterized by the largest curvature.

5 OPTIMIZATION PROCEDURE

5.1 Objective Function

In inverse design, the primary objective is the align-

TRANSONIC AIRFOIL DESIGN BY THE INVERSE METHOD USING VARIABLE-FIDELITY MODELLING

477

ment between the pressure distribution of the airfoil

being designed and the prescribed target. The

alignment can be measured using a norm.

(a)

(b)

Figure 3: (a) Example low-fidelity model pressure

distribution at the design x

(i)

, C

p.c

(i)

) (solid line), the low-

fidelity model pressure distribution at other design x,

p.c

(x) (dotted line), characteristic points of C

p.c

(i)

)

(circles) and C

p.c

(x) (squares), and the translation vectors

(short lines); (b) low-fidelity model pressure distributions,

initial characteristic points (large markers) and translation

vectors from Fig. 3(a) as well as additional points (small

markers) inserted in between the initial points either

uniformly with respect to x/c (for those parts of the

pressure distribution that are almost flat) or based on the

relative pressure value with respect to corresponding

initial points (for those parts of the pressure distribution

that are “steep”).

Due to unavoidable misalignment between the

pressure distributions of the high-fidelity model and

its SPRP surrogate, it is not convenient to use some

of the constraints (e.g., a maximum allowable drag)

directly. This is because the design that is feasible

for the surrogate model, may not be feasible for the

high-fidelity model. In particular, the design

obtained as a result of optimizing the surrogate

model C

p.s

(i)

, i.e., x

(i+1)

, will be feasible for C

p.s

(i)

However, if x

(i+1)

is not feasible for the high-fidelity

model, it will not be feasible for C

p.s

(i+1)

because we

have C

p.s

(i+1)

) = C

p.f

(i+1)

) by the definition of

the surrogate model. In order to alleviate this

problem, we shall use the penalty function approach

to handle the drag constraint. Of course, this does

not apply to constraints that depend exclusively on

the airfoil geometry, such as the minimum airfoil

cross-sectional area.

(a)

(b)

Figure 4: (a) High-fidelity model pressure distribution at

(i)

, C

p.f

(i)

) (solid line) and the predicted high-fidelity

model C

at x (dotted line) obtained using SPRP based on

characteristic points of Fig. 3(b); characteristic points of

p.f

(i)

) (circles) and the translation vectors (short lines)

were used to find the characteristic points (squares) of the

predicted high-fidelity model pressure distribution (only

initial points are shown for clarity); low-fidelity model

distributions C

p.c

(i)

) and C

p.c

(x) are plotted using thin

solid and dotted line, respectively; (b) high-fidelity model

pressure distribution at x, C

p.f

(x) (solid line), and the

predicted high-fidelity model pressure distribution at x

obtained using SPRP (dotted line).

In this work, all the constraints are handled

through penalty functions so that the objective

function is defined as follows



( ( )) ( ( ))

(()) ()

pdwsp

ls p

HC F C C

CC A

















 



(4)

with F = ||C

(x) – C

p.t

||, where C

p.t

is the target

pressure distribution, C

dw.s

= 0 if C

dw.s

≤ C

dw.s.max

and C

dw.s

= C

dw.s

– C

dw.s.max

otherwise, C

l.s

= 0 if

l.s

 C

l.s.min

and C

l.s

= C

l.s

– C

l.s.min

otherwise, and

A = 0 if A ≥ A

min

and A = A – A

min

otherwise. In

our numerical experiments we use







= 1000.

Here, the pressure distribution for the surrogate

model is C

= C

p.s

, and for the high-fidelity model C

= C

p.f

. Also, C

l.s

and C

dw.s

denote the lift and wave

drag coefficients (both being functions of the

pressure distribution).

5.2 Basic Optimization Algorithm

The basic optimization algorithm (Leifsson and

0 0.2 0.4 0.6 0.8 1

-1

-0.5

0.5

1.5

0 0.2 0.4 0.6 0.8 1

-1

-0.5

0.5

1.5

0 0.2 0.4 0.6 0.8 1

-1

-0.5

0.5

1.5

0 0.2 0.4 0.6 0.8 1

-1

-0.5

0.5

1.5

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

478

Koziel, 2011) exploits the SPRP-based surrogate

model and a trust-region convergence safeguard

(Conn et al., 2000). It can be summarized as follows:

1. Set i = 0; Select



(initial trust region radius);

Evaluate C

p.f

(0)

);

2. Set up SPRP model;

3. Obtain x

(i+1)

= argmin{l ≤ x ≤ u, ||x – x

(i)

|| ≤



H(C

p.s

(i)

(x))};

4. Evaluate high-fidelity model to get C

p.f

(i)

);

5. If H(C

p.f

(i)

(i+1)

)) < H(C

p.f

(i)

)) accept x

(i+1)

;

Otherwise x

(i+1)

= x

(i)

;

6. Update



;

7. Set i = i + 1;

8. If termination condition is not satisfied, go to 2.

9. END

The SPRP surrogate model is updated before each

iteration of the optimization algorithm using the

high-fidelity model data at the design obtained in the

previous iteration. The trust-region parameter



updated after each iteration, i.e., decreased if the

new design was rejected or if the improvement of

the high-fidelity model objective function was too

small compared to the prediction given by the SPRP

surrogate, or increased otherwise. We use classical

updating rules (Conn et al., 2000; Koziel et al.,

2006). The algorithm is terminated if ||x

(i+1)

– x

(i)

|| <

0.001 or



< 0.001.

5.3 Improved Optimization Scheme

In algorithm of Section 5.2, the new solution x

(i+1)

obtained by optimizing the SPRP model, which

involves multiple evaluations of the low-fidelity

model. In our case, the low-fidelity model is about

50 times faster than the high-fidelity one, and a

typical surrogate model optimization requires 50 to

100 low-fidelity model calls. Thus, the low-fidelity

model evaluations are responsible for about 50 to 70

percent of the total optimization cost.

In this section, we formulate the improved

optimization scheme that aims at reducing the

aforementioned computational overhead. The idea is

to replace the low-fidelity model—at some point

during the optimization run—by its response surface

approximation model. This replacement is executed

if ||C

p.c

(i–1)

) – C

p.c

(i)

)|| <



max

where



max

is a user-

defined threshold value (here, we use



max

= 0.05).

This allows us to avoid constructing the response

surface model in the entire design space (which

would be too expensive in terms of the number of

necessary data points), but only in the vicinity of the

current solution x

(i)

. In this work, we use kriging

interpolation (Queipo et al., 2005) as the response

surface model. The model is set up using N

= 20

low-fidelity model evaluations allocated—using

Latin Hypercube Sampling (Beachkofski and

Grandhi, 2002)—in the interval [x

(i)

–



, x

(i)



where



= [0.001 0.04 0.005]

The improved algorithm can be summarized as

follows:

1. Set i = 0; Select



(initial trust region radius); Set

the model selector L = 0; Evaluate C

p.f

(0)

);

2. If L = 0 set up SPRP model using the low-

fidelity model; Otherwise, set up SPRP model using

the kriging model of C

p.c

;

3. Obtain x

(i+1)

= argmin{l ≤ x ≤ u, ||x – x

(i)

|| ≤



H(C

p.s

(i)

(x))};

4. Evaluate high-fidelity model to get C

p.f

(i)

);

5. If H(C

p.f

(i)

(i+1)

)) < H(C

p.f

(i)

)) accept x

(i+1)

;

Otherwise x

(i+1)

= x

(i)

;

6. Update



;

7. Set i = i + 1;

8. If L = 0 and ||C

p.c

(i–1)

) – C

p.c

(i)

)|| <



max

, set

L = 1 and set up the kriging model of C

p.c

in the

interval [x

(i)

–



, x

(i)



];

9. If termination condition is not satisfied, go to 2.

10. END

In practice (cf. Section 6), the condition ||C

p.c

(i–1)

) –

p.c

(i)

)|| <



max

is satisfied after one or two

iterations which allows us to substantially reduce the

number of low-fidelity model evaluations in the

optimization process.

6 NUMERICAL EXAMPLES

6.1 General Setup

The proposed optimization method is applied to the

inverse design optimization of four cases. Designs

are obtained using the basic algorithm in Section

5.2, and the improved algorithm in Section 5.3. The

surrogate model optimization is performed using the

pattern-search algorithm

(Koziel, 2010b). For

comparison purposes, designs obtained through

direct optimization of the high-fidelity model using

the pattern-search algorithm

(Koziel, 2010b) are also

presented.

The design variables are the airfoil shape

parameters in the NACA four-digit parameterization

(Section 2), i.e., x = [m p t]

. Note that the chord

length is set to 1. The only inequality constraint is

the minimum cross-sectional area constraint. There

TRANSONIC AIRFOIL DESIGN BY THE INVERSE METHOD USING VARIABLE-FIDELITY MODELLING

479

are no equality constraints. The side constraints are 0

≤ m ≤ 0.1, 0.2 ≤ p ≤ 0.8, and 0.05 ≤ t ≤ 0.20. The test

cases were chosen only for verification purposes and

they do not represent optimal airfoil designs.

6.2 Results of Case Studies

The numerical results of the case studies are

presented in Table 1. The target pressure distribution

is the same for cases 1, 2, and 3, i.e., x = [0.0163

0.4004 0.1118]

with M



= 0.75 and α = 0°. In case

1 the initial design is NACA 2412 and A

min

= 0.078.

For case 1, both the basic and the improved

algorithms hit the cross-sectional area constraint and

match the target pressure distribution only relatively

closely (F = 0.0243 and F = 0.0246, respectively).

However, the improved algorithm requires 5

equivalent high-fidelity model evaluations, while the

basic algorithm needs 18. The direct optimization of

the high-fidelity model required 201 model

evaluations.

In case 2, the constraint value is lowered to

min

= 0.075, while keeping other parameters the

same. Now the algorithms are able to match the

target distribution much closer (F = 0.0025 and F =

0.0011, respectively) with the design cost of about

13 equivalent high-fidelity function calls for the

basic algorithm, and 5 for the improved version.

Figure 5 shows the pressure distributions of the

initial and optimized designs. The high-fidelity CFD

model and the pattern-search algorithm required 152

model evaluations.

Table 1: Numerical results of four inverse design case

studies using the proposed optimization methodology. F is

the norm of the difference of pressure distributions for the

optimized and the target designs. N

is the number of low-

fidelity model evaluations and N

is the number of high-

fidelity model evaluations. All the numerical values are

from the high-fidelity model.

Case 1



= 0.75,



= 0°, A

min

= 0.078

Variable Initial Target

Pattern-

SPRP

Improved

SPRP



M 0.0200 0.0163 0.0153 0.0154 0.0155

P 0.4000 0.4004 0.4089 0.4043 0.3985

T 0.1200 0.1118 0.1159 0.1158 0.1159

0.4745 0.3832 0.3663 0.3663 0.3671

0.0115 0.0049 0.0049 0.0050 0.0052

A 0.0808 0.0753 0.0780 0.0780 0.0781

F N/A N/A 0.0249 0.0243 0.0246

N/A N/A 0 330 70

N/A N/A 201 11 3

Total

cost

N/A N/A 201 < 18 < 5

Case 2



= 0.75,



= 0°, A

min

= 0.075

Variable Initial Target

Pattern-

SPRP

Improved

SPRP



M 0.0200 0.0163 0.0162 0.0162 0.0163

P 0.4000 0.4004 0.4007 0.4014 0.4011

T 0.1200 0.1118 0.1122 0.1121 0.1119

0.4745 0.3832 0.3816 0.3822 0.3829

0.0115 0.0049 0.0049 0.0048 0.0049

A 0.0808 0.0753 0.0756 0.0755 0.0753

F N/A N/A 0.0025 0.0025 0.0011

N/A N/A 0 240 70

N/A N/A 152 8 3

Total

cost

N/A N/A 152 < 13 < 5

Case 3



= 0.75,



= 0°, A

min

= 0.075

Variable Initial Target

Pattern-

SPRP

Improved

SPRP



m 0.0000 0.0163 0.0156 0.0163 0.0161

p 0.5000 0.4004 0.4252 0.3978 0.4030

t 0.1000 0.1118 0.1139 0.1117 0.1126

0.0005 0.3832 0.3776 0.3835 0.3801

0.0002 0.0049 0.0045 0.0049 0.0048

A 0.0673 0.0753 0.0767 0.0752 0.0758

F N/A N/A 0.0181 0.0023 0.0048

N/A N/A 0 468 70

N/A N/A 201 6 5

Total

cost

N/A N/A 201 < 16 < 7

Case 4



= 0.75,



= 1°, A

min

= 0.065

Variable Initial Target

Pattern-

SPRP

Improved

SPRP



m 0.0000 0.0300 0.0287 0.0293 0.0300

p 0.4000 0.2000 0.2067 0.2057 0.2000

t 0.1200 0.1000 0.1083 0.1022 0.1000

0.2082 0.8035 0.7786 0.7905 0.8034

0.0024 0.0410 0.0424 0.0405 0.0410

A 0.0808 0.0675 0.0731 0.0689 0.0675

F N/A N/A 0.0492 0.0182 0.00097

N/A N/A 0 457 120

N/A N/A 202 6 9

Total

cost

N/A N/A 202 < 16 < 12

Design obtained using the high-fidelity model and the grid-

search algorithm (Koziel, 2010b).

Design obtained using the basic algorithm of Section 5.2;

surrogate model optimization performed using the grid-search

algorithm (Koziel, 2010b).

Design obtained using the improved algorithm proposed in

Section 5.3; surrogate model optimization performed using the

grid-search algorithm (Koziel, 2010b).

The total optimization cost is expressed in terms of the

equivalent number of high-fidelity model evaluations. The ratio

of the high-fidelity model evaluation time to the corrected low-

fidelity model evaluation time varies between 13.5 to 73

depending on the design. For the sake of simplicity we use a fixed

value of 50 here.

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

480

(a)

(b)

Figure 5: The pressure distributions and airfoil shapes for

the initial and optimized designs for case 2.

Case 3 starts with a different initial design,

namely, the NACA 0010. Here, both algorithms

match the target closely. The basic algorithm

requires 16 equivalent high-fidelity function calls,

whereas the improved algorithm 7.

In case 4, the target pressure distribution is the

one of NACA 3210 at M



= 0.75 and α = 1°. The

initial design is NACA 0012 and the minimum

cross-sectional area is A

min

= 0.065. The improved

algorithm is able to match the target closely in less

than 12 equivalent high-fidelity model evaluations.

The basic algorithm and the direct pattern-search are

both unable to match the target closely.

7 CONCLUSIONS

Computationally efficient variable-fidelity design of

transonic airfoils is presented. The algorithm replaces

the direct optimization of a CPU-intensive high-

fidelity CFD model by iterative updating and re-

optimization of its fast surrogate. The surrogate is

constructed using a shape-preserving response

prediction technique with the underlying low-fidelity

CFD model, which is replaced—after a few

iterations—by its local response surface

approximation. The operation and performance of our

algorithm is demonstrated using several transonic

airfoil design cases with the optimized designs

obtained at a low cost corresponding to a few high-

fidelity CFD simulations. Our results indicate that the

algorithm presented here is computationally much

more efficient than its basic version that only exploits

the corrected CFD low-fidelity model but not the

response surface one.

REFERENCES

Abbott, I. H., and Von Doenhoff, A. E., 1959, Theory of

Wing Sections, Dover Publications, 1959.

Alexandrov, N. M., Lewis, R. M., Gumbert, C. R., Green, L.

L., and Newman, P. A., 2000, Optimization with

Variable-Fidelity Models Applied to Wing Design, 38th

Aerospace Sciences Meeting & Exhibit, Reno, NV, AIAA

Paper 2000-0841.

Barrett, T. R., Bressloff, N. W., and Keane, A. J., 2006,

Airfoil Design and Optimization Using Multi-Fidelity

Analysis and Embedded Inverse Design, AIAA Paper

2006-1820, 47th AIAA/ASME/ASCE/AHS/ASC

Structures, Structural Dynamics, and Materials

Conference, Newport, Rhode Island.

Beachkofski B. and Grandhi R., 2002. Improved

distributed hypercube sampling. American Institute of

Aeronautics and Astronautics, paper AIAA 2002-

1274.

Booker, A.J., Dennis Jr., J.E., Frank, P.D., Serafini, D.B.,

Torczon, V., and Trosset, M.W., 1999, A rigorous

framework for optimization of expensive functions by

surrogates, Structural Optimization, vol. 17, no. 1, pp. 1-

13.

Braembussche, R. A., 2008, Numerical Optimization for

Advanced Turbomachinery Design, In Optimization

and Computational Fluid Dynamics, Thevenin, D. and

Janiga, G., editors, Springer, pp. 147-189.

Conn, A. R., Gould, N. I. M., and Toint, P. L., 2000, Trust

Region Methods, MPS-SIAM Series on Optimization.

Dulikravich, G. S., 1991, Aerodynamic Shape Design and

Optimization, 29th AIAA Aerospace Sciences Meeting,

Reno, NV.

FLUENT, ver. 12.1, ANSYS Inc., Southpointe, 275

Technology Drive, Canonsburg, PA 15317, 2006.

Forrester, A. I. J., and Keane, A. J., 2009, Recent advances in

surrogate-based optimization, Progress in Aerospace

Sciences, vol. 45, no. 1-3, pp. 50-79.

ICEM CFD, ver. 12.1, ANSYS Inc., Southpointe, 275

Technology Drive, Canonsburg, PA 15317, 2006.

Koziel, S., Bandler, J. W., and Madsen, K., 2006, Space-

mapping based interpolation for engineering

optimization. IEEE Trans. Microwave Theory and

Tech., 54 (6), pp. 2410–2421.

Koziel, S., Cheng, Q. S., and Bandler, J. W., 2008, Space

mapping, IEEE Microwave Magazine, vol. 9, no. 6,

pp. 105-122.

Koziel, S., 2010a, Shape-preserving response prediction

for microwave design optimization, IEEE Trans.

Microwave Theory and Tech., vol. 58, pp. 2829-2837.

Koziel, S., 2010b, Multi-fidelity multi-grid design

optimization of planar microwave structures with

Sonnet. International Review of Progress in Applied

Computational Electromagnetics, Tampere, Finland,

pp. 719-724.

Labrujere, T. E. and Slooff, J. W., 1993, Computational

Methods for the Aerodynamic Design of Aircraft

Components, Annual Review of Fluid Mechancis, vol. 25,

pp. 183-214.

0 0.2 0.4 0.6 0.8 1

-1

-0.5

0.5

1.5

Initial

Optimized

0 0.2 0.4 0.6 0.8 1

-0.05

0.05

0.1

z/c

TRANSONIC AIRFOIL DESIGN BY THE INVERSE METHOD USING VARIABLE-FIDELITY MODELLING

481

Lane, K. A., and Marshall, D. D., 2010, Inverse Airfoil

Design Utilizing CST Parameterization, 48th AIAA

Aerospace Sciences Meeting Including the New Horizons

Forum and Aerospace Exposition, Orlando, Florida.

Leifsson, L., and Koziel, S., 2010, Multi-fidelity design

optimization of transonic airfoils using physics-based

surrogate modeling and shape-preserving response

prediction, Journal of Computational Science, vol. 1, no.

2, pp. 98-106.

Leifsson, L., and Koziel, S., 2011, Inverse Design of

Transonic Airfoils Using Variable-Resolution Modeling

and Pressure Distribution Alignment, International

Conference on Computational Science, Singapore, June

1-3.

Leoviriyakit, K., Kim, S., and Jameson, A., 2003, Viscous

Aerodynamic Shape Optimization of Wings including

Planform Variables, 21st Applied Aerodynamics

Conference, Orlando, Florida, June 23-26.

Robinson, T. D., Eldred, M. S., Willcox, K. E., and Haimes,

R., 2008, Surrogate-Based Optimization Using

Multifidelity Models with Variable Parameterization and

Corrected Space Mapping, AIAA Journal, vol. 46, no. 11.

Tannehill, J. A., Anderson, D. A., and Pletcher, R. H.,

1997, Computational fluid mechanics and heat

transfer, 2

edition, Taylor & Francis.

Queipo, N. V., Haftka, R. T., Shyy, W., Goel, T.,

Vaidynathan, R., and Tucker, P.K., 2005, Surrogate-

Based Analysis and Optimization. Progress in

Aerospace Sciences, 41(1), pp. 1-28.

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

482