
A NEW METHOTOLOGY FOR ADAPTIVE FUZZY
CONTROLLER. COMPARISON PERFORMANCE AGAINST
SEVERAL CONTROL ALGORITHMS IN A REAL TIME
CONTROL PROCESS
Rafik Lasri, Ignacio Rojas, Héctor Pomares and Fernando Rojas
Dep. Computer Architecture & Computer Technology, E.T.S. Ing. Informática & Telecomunicación
Univ. of Granada, Periodista Daniel Saucedo Aranda, s/n, E-18071, Granada, Spain
Keywords: Adaptive Fuzzy Controller, Temperature Control, Real-time Control, PID Control Process.
Abstract: This article presents a comparative study of various control algorithms. An adaptive fuzzy logic controller is
set to prove its effectiveness against other conventional controllers in a simulated control process as well as
in a real environment. Through a training board that allows us to control the temperature, we can compare
the behavior of each used algorithm. The adaptive fuzzy logic controller will be required to present a real
high performance in temperature control, having in mind that the adaptive algorithm starts with no rules set
i.e., empty rule base or by assigning arbitrary values to the rules without any information off-line. The
comparison of results clearly shows the great contribution that the policy of an adaptive algorithm brings;
ease of implementation and high accuracy.
1 INTRODUCTION
An intelligent control system typically consists of
two parts: the firstis the “knowledge base” which
presents the necessary knowledge to control the
plant, and the second is an “inference engine” which
processes the knowledge through reasoning,
possibly using a new set of data to obtain the
decision. Our study uses intelligent control
techniques based on fuzzy logic and PID controller
structures. Several structures of controllers have
been tested in this control process to demonstrate the
profitability of our adaptive fuzzy controller.
During the past 30 years numerous studies have
presented several examples of adaptive controllers.
In the 70sE.H. Mamdani and his student S. Assilian
(Mamdani and Assilian, 1975) to determine the
responsible rule for the undesirable state of the plant
and replace it with the appropriate value, these steps
have initialized a new policy of adaptive fuzzy logic
controllers it calling Self Organizing Control (SOC)
system (Procyk, 1979). In most SOC approaches,
this dependence is expressed using only the
monotonicity sign of the plant (Cho, 2002; Fan,
2004; Hua, 2004; K.Lin, 2003; M.Lin, 2004; Park,
2005; Velagic, 2003; Velez-Diaz, 2004; Yi, 2002).
The main focus of this paper is to prove that our
adaptive fuzzy controller is capable of achieving a
high accuracy and a good robustness through
modifying the consequents of the rules in real time,
the controller determines in which sense the rules
have to be moved i.e., auto-learning. The proposed
methodology is robust against modification of the
parameters of the plant (break-downs). It is
important to note, that no initial knowledge about
the control policy is required and therefore the fuzzy
controller can start with a set of empty rules.
2 TEMPERATURE CONTROL:
THE HARDWARE
DESCRIPTION
In this paper we will try to simulate the control of
temperature of a room using a training board with
several intelligent control algorithms. Our goal is to
maintain the temperature of the room at a desired
value; the room is equipped with a temperature
source that heats the environment and a fan for
470
Lasri R., Rojas I., Pomares H. and Rojas F..
A NEW METHOTOLOGY FOR ADAPTIVE FUZZY CONTROLLER. COMPARISON PERFORMANCE AGAINST SEVERAL CONTROL ALGORITHMS
IN A REAL TIME CONTROL PROCESS.
DOI: 10.5220/0003647204700474
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FCTA-2011), pages 470-474
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
lowering the temperature in cases of over passing
the set point. The controller will aim to generate the
fan power signal and determining their performance
rating regard to the difference between the sensed
temperature inside the room and the required
temperature.
3 DESIGN AND
IMPLEMENTATION OF THE
USED CONTROLLERS
3.1 Tuning the PID Controllers
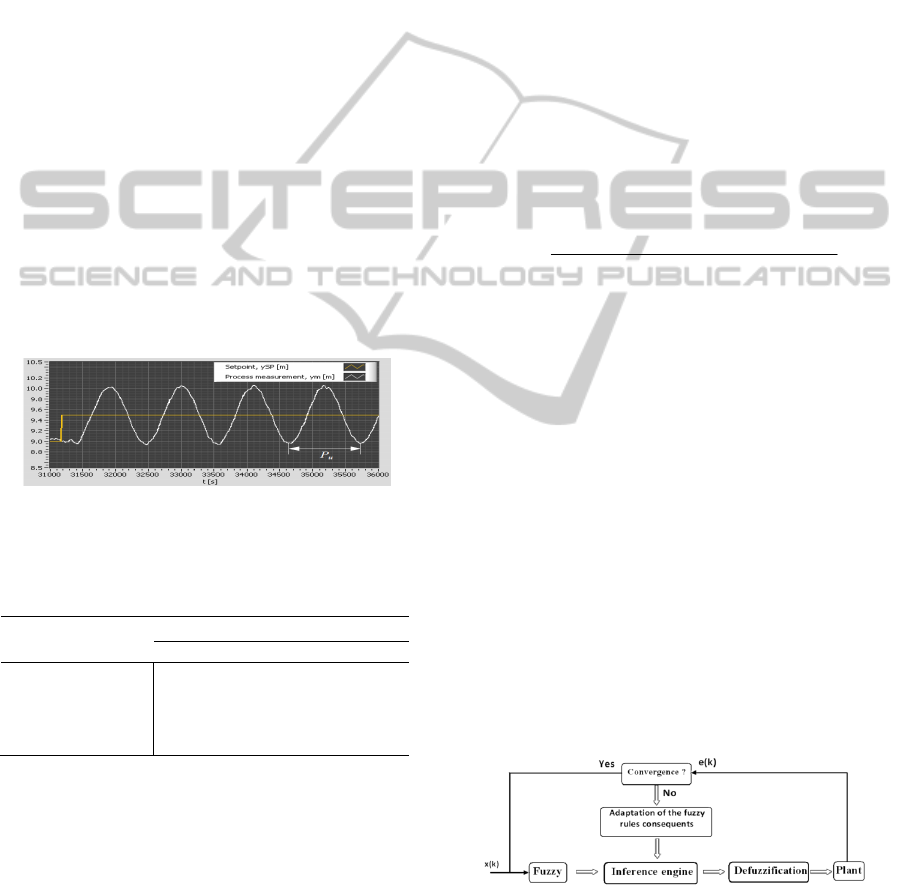
The Ziegler–Nichols closed loop (Ziegler, 1942),
tuning method is a heuristic method of tuning a PID
controller. It is performed by setting the I (integral)
and D (derivative) gains to zero. The P
(proportional) gain is then increased (from zero)
until it reaches the ultimate gain K
u
, at which the
output of the control loop oscillates with a constant
amplitude. K
u
and the oscillation period P
u
are used
to set the P, I, and D gains depending on the type of
controller used.
Figure 1: Ideal tuning phase of the Ziegler-Nichols closed
loop method.
Table 1: Formulas for the controller parameters in the
Ziegler-Nichols closed loop method.
Structures Parameters
Kp Ti Td
P controller
PI controller
PID controller
0.5 Kp
u
∞ 0
0.45Kp
u
P
u
/ 1.2 0
0.6 Kp
u
P
u
/ 2 P
u
/ 8
3.2 Design of a Static Fuzzy Logic
Controller
Due to its simplicity and stability we chose a TSK-0
fuzzy logic controller (static controller), with two
inputs and one output. The controller inputs are the
temperature error and its derivative (Te, Tė), the
error is the difference between the required
temperature Tsp and the temperature at instant i (Ti),
in fact the error equation is: Te = Tsp – Ti. The
controller output is the tension that controls the fan
operation. The inputs have a set of membership
functions describing the state of these variables in
their natural space, limited by its real extreme limits.
The first input has seven and the second one has fife
triangular membership functions covering the whole
range of variation. The output is a set of scalar
values (TSK-0 type controller).
3.3 Implementation of an Advanced
(Adaptive) Fuzzy Logic Controller
in Real Time
In this article, we used the product as T-norm for the
fuzzy inference method and the ‘‘centre of gravity’’
with sum-product operator as the defuzzification
strategy. Using the above notation, we can express the
output of the fuzzy controller as follows:
⎛⎞
⋅
⎜⎟
⎝⎠
⎛⎞
⎜⎟
⎝⎠
∑∑ ∑ ∏
∑∑ ∑ ∏
"
G
"
N
12
i
v
12 N
v
12 N
N
12
i
v
v
12 N
n
nn
N
k
i i ...i v
X
i=1i=1 i =1 v=1
k
n
nn
N
k
v
X
i=1i=1 i =1 v=1
R
μ
(x )
F(x ) =
μ (x )
(1)
where
is the N-dimensional input vector at
instant k. The adaptive algorithm used, will be able
to adapt the controller parameters using the
information obtained from the current error in the
output of the plant. The correction sense is deduced
from the monotony of the plant.
In the algorithm subject of this study, coarse
adaptation of the fuzzy rule consequents is achieved
by evaluating the current state of the plant and
proposing a correction of the rules responsible for
the existence of such a state, either as a reward or as
a penalty, in the following way:
(2)
where:
µi
1
i
2
...i
N
is the strength or α-level of rule
R
i
1
i
2
...i
N
, and e
y
(k) is the error at instant k.
Figure 2: Adaptive fuzzy controller.
Since, as in (Rojas, 1999), the degree with which the
rule was activated in achieving the control output
u(k-d) was used proportionally with the modification
k
x
G
()
)()()·(·
)()·(·)(
...
......
21
2121
kydkrdkC
kedkCkR
N
NN
iii
yiiiiii
−−−
=−=Δ
μ
μ
A NEW METHOTOLOGY FOR ADAPTIVE FUZZY CONTROLLER. COMPARISON PERFORMANCE AGAINST
SEVERAL CONTROL ALGORITHMS IN A REAL TIME CONTROL PROCESS
471
adopted now being evaluated at instant k. In the
aforementioned expression, d represents the time
delay, r(k-d) is the required set point of the plant
output at instant k-d and y(k) is the current plant
output, it is very important to clear up that using r(k)
would be incorrect, because the rules that are
activated at instant k-d serve to achieve the desired
value r(k-d) and not r(k). The determination of the
absolute value of the coefficient C is calculated
spent in off-line using the formula: |C| = ∆u/∆y,
where ∆y is the operation range of the plant output ,
which must be estimated beforehand from the
knowledge about the set points that we are going to
use, and ∆u is the operation range of the controller’s
actuator. In our case and after studying our plant we
chose |C|= 15.
4 SIMULATION RESULTS
4.1 Real Simulation: Temperature
Control
The MSE calculated in this study is not the MSE of
the function approximation by the controller but it‘s
the MSE between the set point and the plant output
measured after d instants of time, being d the delay
of the plant.
MSE =
∑
(
(
)
())
_
_
(3)
4.1.1 Temperature Control Using a P, I and
D Control Policy
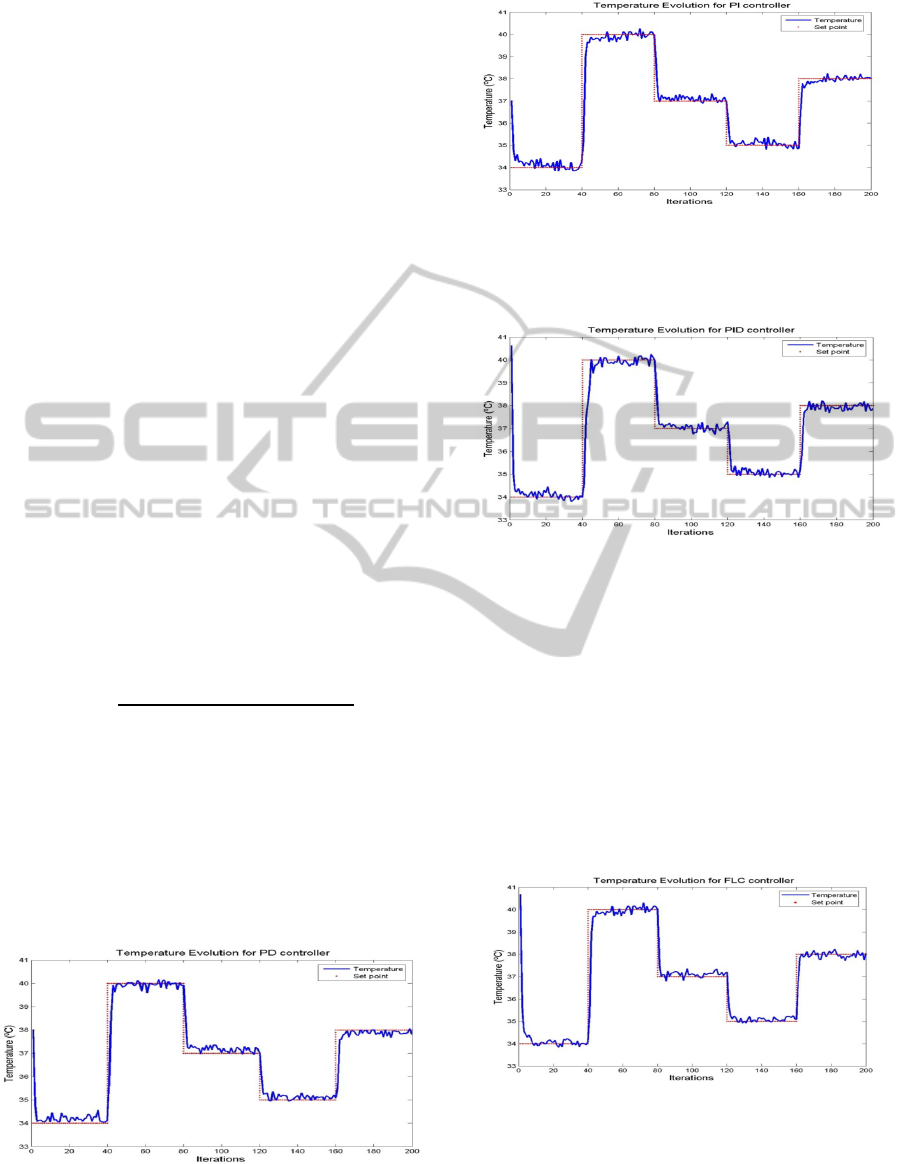
• The PD and PI Controllers
The PD and PI controllers have been able to control
the temperature, the MSE (mean squared error) for
the last 40 iterations are respectively around 0.49
(Fig. 3) and 0.43 (Fig. 4).
Figure 3: Control evolution with PD algorithm for various
set points.
Figure 4: Control evolution with PI algorithm for various
set points.
• Using a Full PID Controller
Figure 5: Control evolution with PID algorithm for various
set points.
Fig. 5 clearly shows that our PID works well as a
controller for various values of set points,
guaranteeing the convergence around the set point
with a 0.47 MSE in the last 40 iterations.
4.1.2 Temperature Control using a Static
Fuzzy Logic Controller
Fig. 6 shows that the static fuzzy logic controller is
performing well. The MSE for the last 40 iterations
is 0.31.
Figure 6: Control evolution with FLC algorithm for
various set points.
4.1.3 Temperature Control using Adaptive
Fuzzy Logic Controller
An analysis of the MSE in the last 40 iterations
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
472
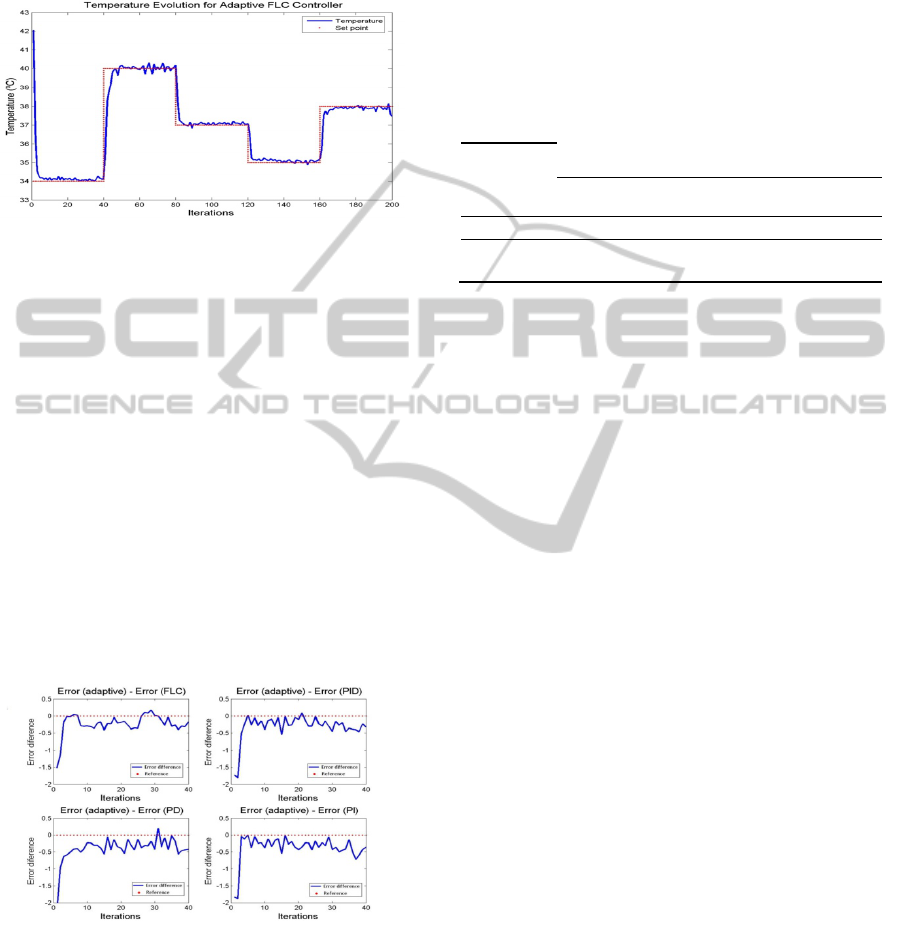
shows clearly the superiority of the latter compared
with others; the adaptive
algorithm has been able to
reduce the error to almost 50%. The MSE in this
case is 0.17.
Figure 7: Control evolution with adaptive FLC algorithm
for various set points.
4.2 Results Comparison
The graphical method consists in drawing the
representing curve of the difference between the
errors committed by two different algorithms at the
same time interval and to achieve the same set point,
i.e, represents the function defined as:
Error difference = E
(Algorithm 1)
- E
(Algorithm 2)
(4)
If E
(Algorihtm 1)
> E
(Algorithm 2)
Î Error difference > 0
The graphical representation of the function Error
difference is above zero.
If E
(Algorithm 1)
< E
(Algorithm 2)
Î Error difference < 0
The graphical representation of the function Error
difference is under zero.
Figure 8: Differences between the error committed by the
Adaptive FLC and the remaining algorithms.
The four cases presented in Fig. 8 show that the
error difference curve is almost always under the
zero line, mathematically this means that:
Error difference = E
(Algorithm 1)
- E
(Algorithm 2)
< 0
Î E
(Algorithm 1)
< E
(Algorithm 2)
In our case: E
(Algorithm 1)
is E
(Adaptive)
.
The Error difference is almost always less than
zero in the four cases, that means that the E
(Adaptive)
is less than the rest of committed errors by others
algorithms E
(FLC,PID,PD,PI)
.
The numerical comparison (Table 2) is based on the
analysis of the MSE for each algorithm.
Table 2: Comparative performance indices for all used
algorithms in real simulation.
MSE
Algorithms
PI PD PID
Classic
FLC
Adaptive
FLC
MSE
160
Î
200
0.43 0.49 0.47 0.31 0.17
MSE
100
Î
200
0.38 0.44 0.41 0.28 0.23
MSE
0
Î
200
0.84 0.89 0.85 0.78 0.67
The results presented in this table show the
differences between the algorithms used. The
adaptive controller has the best error reduction
compared to the other, i.e., the adaptation presented
and tested by I. Rojas et.al (Rojas, 2006) is a good
alternative to replace the P, I, D controllers or a
classical fuzzy logic controller for these kinds of
plants.
4.3 The Perturbation Effects on the
behavior Algorithm
Fig. 9 depicts the behavior of the algorithms (static
FLC and Adaptive FLC) after a disturbance of 25%
at iteration number 20. The disturbance used here is
a simulation of a temperature decrease caused by a
secondary fan and at the 65 iteration, we have
caused a disturbance of 20% but this time we
simulate a temperature increase caused by another
source of temperature. The response of the plant
after the disturbances for each algorithm can clearly
explain the differences between every one of them.
Top of Figure 9 shows the behavior of static FLC
in perturbation cases. We can notice how these
disturbances can affect the control precision; the
static FLC keeps the plant under control but with
large error without over passing the perturbation
effects.
In the bottom graph the adaptive FLC presents a
very good performance against these disturbances. It
can be clearly noticed that the control precision does
not suffer big changes and that the adaptive
algorithm can overcome the perturbation effects in
few moments later.
Table 3 presents a numerical comparison
between the error committed in 10 iterations before
causing the disturbances and the error committed in
A NEW METHOTOLOGY FOR ADAPTIVE FUZZY CONTROLLER. COMPARISON PERFORMANCE AGAINST
SEVERAL CONTROL ALGORITHMS IN A REAL TIME CONTROL PROCESS
473
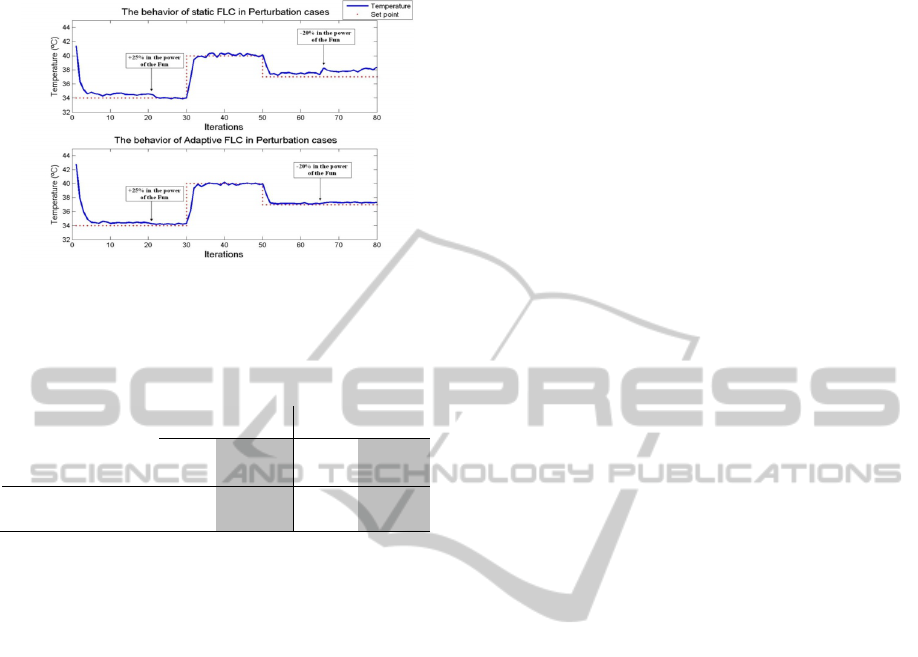
10 iterations with disturbance for each algorithm.
Figure 9: The perturbation effects on the control
performance.
Table 3: Comparative performance indices before and
after the perturbation.
MSE in 10 iterations
+ %25 in the
power of the Fan
- %20 in the power
of the Fan
FLC
Adapt
FLC
FLC
Adapt
FLC
Before perturbation
0.78 0.42 0.64 0.1
After perturbation
0.32 0.36 1.77 0.14
It is important to clear here that the error
reduction in the first case of perturbation doesn’t
mean a control improvement, it’s due to the new Fan
added by simulation, adding a Fan with power more
bigger signify big reduction in the error committed
and maybe the error will change the sign if this Fan
power was too much. The MSE presented in this
table proves that the perturbation effects on the
behavior of the adaptive algorithm are very small
when compared with their effects on the behavior of
the FLC algorithm.
5 CONCLUSIONS
This paper presents a comparative study between
several control algorithms and an adaptive fuzzy
logic controller. Both, the conventional fuzzy logic
controller and the P, I and D controller structure
show their capabilities to control the plant with a
reasonable error. The adaptive algorithm without
any off line pre-training and starting with no definite
rule base has been able to improve the committed
error during the control process. The adaptive
algorithm does not need any complex mathematical
models. It only needs a limited information from the
plant.The monotonicity and the delay of the plant,
were the only information used by the adaptive
algorithm to optimize the error at the plant output.
The results comparison can prove the superiority of
the proposed adaptive FLC controller against the
remaining of algorithms.
ACKNOWLEDGEMENTS
This work has been supported by the Genil Start-up
Project “Processing and Classification of Electro-
oculography (EOG) Data for Ataxia SCA-2
Diagnosis” (PYR-2010-23) from the CEI bioTIC
GENIL (CEB09-0010) of the CEI program from the
MICINN.
REFERENCES
Rojas, I., Pomares, H., González, J., Herrera, L. J., Guillen
,A., Rojas ,F., Valenzuela ,O., 2006. Adaptive fuzzy
controller: Application to the control of the tem-
perature of a dynamic room in real time, Fuzzy Sets
and Systems 157, 2241 – 2258.
Fan, X., Zhang, N., Teng, S., 2004. Trajectory planning
and tracking of ball and plate system using hierar-
chical fuzzy control scheme, Fuzzy Sets and Systems
144 (2) 297–312.
Hua, C., Guan, X., Duan, G., 2004. Variable structure ada-
ptive fuzzy control for a class of nonlinear time-delay
systems, Fuzzy Sets and Systems 148 (3) 453–468.
Lin, C. M., Hsu, C. F., 2004. Adaptive fuzzy sliding-mode
control for induction servomotor systems, IEEE Trans.
Energy Conversion 19 (2) 362–368.
Mamdani, E. H., Assilian, S., 1975. Experiment in
Linguistic Synthesis with a Fuzzy Logic Controller.
International Journal of Man-Machine Studies, 7, 1-
13.
Park, J.-H., Park, G.-T., Kim, S.-H., Moon, C.-J., 2005.
Output-feedback control of uncertain nonlinear
systems using a self-structuring adaptive fuzzy
observer, Fuzzy Sets and Systems 151 21–42.
Velagic, J., Vukic, Z., Omerdic, E., 2003. Adaptive fuzzy
ship autopilot for track-keeping, Control Eng. Practice
11 433–443.
Velez-Diaz, D., Tang, Y., 2004. Adaptive robust fuzzy
control of nonlinear systems, IEEE Trans. Systems,
Man Cybernetics, Part B 34 1596–1601.
Ziegler, J. G., Nichols, N. B., 1942. Optimum Settings for
Automatic Controllers, Trans. ASME, Vol. 64,759-
768.
Yi, J., Yubazaki, N., Hirota, K., 2002. A proposal of
SIRMs dynamically connected fuzzy inference model
for plural input fuzzy control, Fuzzy Sets and Systems
125 (1) 79–92.
Rojas, I., Pomares, H., Pelayo, F. J., Anguita, M., Ros, E.,
Prieto, A., 1999. New methodology for the develop-
pment of adaptive and self-learning fuzzy controllers
in real time, Int. J. Approx. Reason. 21, 109–136.
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
474
