ADAPTIVE LQG CONTROL WITH LOOP TRANSFER RECOVERY
Andrzej Krolikowski and Dariusz Horla
Poznan University of Technology, Institute of Control and Information Egineering, ul. Piotrowo 3a, 60-965 Poznan, Poland
Keywords:
LQG control, Loop transfer recovery, Adaptive control.
Abstract:
An adaptive discrete-time LQG control with loop transfer recovery is considered using shift and delta op-
erators. The control problem is analyzed using state-space model and the parameter estimation problem is
implemented for corresponding ARMAX model. Analysis of asymptotic performance of delta model ap-
proach and continuous-time model case is presented. Computer simulations of third-order system modeled by
a second-order model are given to illustrate the robustness properties of the adaptive LQG/LTR controller.
1 INTRODUCTION
Adaptive LQG control is not an area of a great deal of
research, in particular for adaptive LQG control with
loop transfer recovery (LTR). Adaptive LQG control
has been discussed e.g. in (Bitmead et al., 1990; Tay
and Moore, 1991; Krolikowski, 1995; M¨akil¨a et al.,
1984), where in (Tay and Moore, 1991) an adaptive
LQG/LTR problem was solved augmenting the basic
estimator-based controller with a stable proper linear
system feeding back the estimation residuals. This
idea was also used for non-adaptive continuous-time
systems in (Tay and More, 1989) using the H
∞
/H
2
optimization technique.
In this paper, an application of LTR technique to adap-
tive control of discrete-time systems for both z and
δ operators is presented. The adaptive continuous-
time LQG control algorithm is proposed where the
controller/filter parameters are tuned on the basis of
δ model identification. Asymptotic performance for
lim
T
s
→
0 is analyzed. The robustness issue is touched
and simulated for third-order ARX system considered
as a second-order model.
2 PRELIMINARIES
Consider the following state-space description of the
multivariable linear discrete-time system
x
t+1
= Fx
t
+ Gu
t
+ w
t
(1)
y
t
= Hx
t
+ v
t
(2)
obtained with ZOH where {w
t
} and {v
t
} are se-
quences of independent random vector variables with
zero mean and covariances Ew
t
w
T
s
= Σ
w
δ
t,s
, v
t
v
T
s
=
Σ
v
δ
t,s
.
The Kalman predictor in steady-state is given by
ˆx
t+1/t
= Fˆx
t/t−1
+ Gu
t
+ K
p
˜y
p
t
(3)
where ˜y
p
t
= y
t
− H ˆx
t/t−1
is an innovation of output at
time t. The predictor gain is given by
K
p
= FPH
T
[HPH
T
+ Σ
v
]
−1
(4)
where P is the solution of Riccati equation
P = FPF
T
+ Σ
w
− FPH
T
[HPH
T
+ Σ
v
]
−1
HPF
T
(5)
The covariance of the innovation ˜y
p
t
is Σ
˜y
= HPH
T
+
Σ
v
.
Filtered estimate ˆx
t/t
in terms of ˆx
t/t−1
is
ˆx
t/t
= ˆx
t/t−1
+ K
f
˜y
p
t
(6)
and the recursive equation for ˆx
t/t
is
ˆx
t+1/t+1
= F ˆx
t/t
+ (I − K
f
H)Gu
t
+ K
f
˜y
f
t+1
(7)
where ˜y
f
t+1
= y
t+1
− HF ˆx
t/t
and the filter gain
K
f
= PH
T
[HPH
T
+ Σ
v
]
−1
, (8)
so K
p
= FK
f
in view of (4). An alternative version of
(7) is
ˆx
t+1/t+1
= Fˆx
t/t
+ Gu
t
+ K
f
˜y
p
t+1
(9)
3 LOOP TRANSFER RECOVERY:
z OPERATOR FORMULATION
Consider the stationary loss function
J = E
∞
∑
t=0
y
T
t
y
t
(10)
509
Krolikowski A. and Horla D..
ADAPTIVE LQG CONTROL WITH LOOP TRANSFER RECOVERY.
DOI: 10.5220/0003648005090513
In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICM-2011), pages 509-513
ISBN: 978-989-8425-74-4
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

and assume that the system is square and det(HG) 6=
0.
The control law
u
t
= K
c
x
t/t
(11)
minimizing the loss J is then determined by
K
c
= −(HG)
−1
HF (12)
and the matrix H
T
H is the solution of the correspond-
ing Riccati equation.
The transfer function in z operator G
f
(z) of compen-
sator defined by (7) and (11) can be manipulated into
the form
G
f
(z) = zK
c
[zI − (I − K
f
H)(F − GK
c
)]
−1
K
f
(13)
The filter’s open-loop return ratio is
Φ(z) = H(zI − F)
−1
K
p
(14)
In (Maciejowski, 1985) it was shown that if G(z) =
H(zI− F)
−1
G is minimum-phase and K
c
takes a form
of (12) then the perfect recovery takes place, that is
∆(z) = G(z)G
f
(z) − Φ(z) = 0. (15)
When G(z) is nonminimum-phase then the perfect re-
covery is in general not possible, however the possi-
bility of recovery is frequently realized in closed-loop
bandwidth (Maciejowski, 1985).
In the case of the Kalman predictor feedback, the con-
troller is
u
t
= K
c
x
t/t−1
(16)
and its transfer function is
G
p
(z) = K
c
[zI − F + GK
c
+ K
p
H]
−1
K
p
(17)
Again the perfect recovery cannot be achieved in this
case even for minimum-phase system.
4 LOOP TRANSFER RECOVERY:
δ OPERATOR FORMULATION
State equation (1) in δ operator formulation takes a
form
δx
t
= F
δ
x
t
+ G
δ
u
t
+ w
′
t
(18)
where in view of (1) F
δ
=
1
T
s
(F − I), G
δ
=
1
T
s
G and
w
′
t
=
1
T
s
w
t
, v
′
t
=
1
T
s
v
t
are sequences with spectral den-
sities W and V, respectively. Usually, the δ opera-
tor discretization is used for small T
s
when ZOH dis-
cretization makes numerical problems. The filter’s
open-loop return ratio at the output node of the plant
is
Φ(γ) = H(γI − F
δ
)
−1
K
p
(19)
where δ transform operator with the sampling period
T
s
is γ =
z−1
T
s
.
The LQG controller is defined by the control law
u
t
= K
c
x
t/t
(20)
with the Kalman filter given by
ˆx
t/t
= ˆx
t/t−1
+ +T
s
K
f
˜y
p
t
(21)
where
δˆx
t/t−1
= F
δ
ˆx
t/t−1
+ G
δ
u
t
+ K
p
˜y
p
t
(22)
Moreover, it holds K
p
= (I + T
s
F
δ
)K
f
, and an explicit
recursive equation for Kalman filter is
δˆx
t/t
= F
δ
ˆx
t/t
+ G
δ
u
t
+ K
f
˜y
p
t+1
. (23)
In (Tadjine et al., 1994) it was shownthat if the system
(18), (2) is stabilizable, detectable, left invertible and
inversely stable, and weighting matrices in the perfor-
mance index Q = H
T
H, R = ρI then asymptotically
as ρ → 0, K
c
takes the forms
K
c
= −
1
T
s
(HG
δ
)
−1
H(I + T
s
F
δ
) (24)
and the perfect recovery takes place, that is
∆(γ) = G(γ)G
f
(γ) − Φ(γ) = 0, (25)
where G(γ) = H(γI − F
δ
)
−1
G
δ
, and
G
f
(γ) = (1+ T
s
γ)K
c
[γI − F
δ
+ G
δ
K
c
)]
−1
K
f
(26)
is the transfer function of the controller
u
t
= K
c
x
t/t
(27)
where now
ˆx
t/t
= ˆx
t/t−1
+ +T
s
K
f
y
t
(28)
and
δˆx
t/t−1
= F
δ
ˆx
t/t−1
+ K
p
y
t
. (29)
The above results from the fact that as soon as recov-
ery is obtained the coupling between the observation
error and the observer output should vanish.
5 LOOP TRANSFER RECOVERY:
CONTINUOUS-TIME
FORMULATION
The dynamics of the system is given by the transfer
function matrix from control input to the output
G(s) = C(sI − A)
−1
B, (30)
where A, B,C are matrices in the standard state-space
equation, and C = H. It is worthy to note that asymp-
totically i.e. for T
s
→ 0, G(γ) → G(s), however
G(z) → 0.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
510

Transfer matrix of the controller is
G
f
(s) = K
c
c
[sI − A+ BK
c
c
+ K
c
f
C]
−1
K
c
f
(31)
To compute K
c
c
for the LQG/LTR controller the fol-
lowing Riccati equation is to be solved
P
ρ
A+ A
T
P
ρ
+C
T
C−
1
ρ
P
ρ
BB
T
P
ρ
= 0 (32)
for ρ → 0 and then the controller gain K
c
c
is calculated
as
K
c
c,ρ
= −
1
ρ
B
T
P
ρ
. (33)
The following LTR result holds (Athans,
1986): if the plant G(s) is minimum-phase
then lim
ρ→0
G(s)G
f,ρ
(s) = Φ(s), where
Φ(s) = C(sI − A)
−1
K
c
f
and G
f,ρ
(s) is calculated
from (31) for K
c
c,ρ
. The dual LTR result, i.e. when
the weighting matrix Q = Q
0
+ ρM for ρ → ∞ can be
found in (Kulcsar, 2000). It is easy to see from (26)
that asymptotically
lim
T
s
→0
G
f
(γ) = G
f
(s) = K
c
[sI − A+ BK
c
)]
−1
K
f
(34)
and full recovery holds that is G(s)G
f
(s) = Φ(s), so
the δ model approach and continuous-time case are
asymptotically equivalent. Obviously, it holds K
p
=
K
f
for T
s
→ 0.
To compute K
c
f
in (31) the following Riccati equation
is to be solved
AP
µ
+ P
µ
A
T
+ L
T
L−
1
µ
P
µ
C
T
CP
µ
= 0 (35)
and then the filter gain K
c
f
is calculated as
K
c
f,µ
=
1
µ
P
µ
C
T
. (36)
where µI and L
T
L are intensity matrices for measure-
ment and system noise, respectively.
6 ADAPTIVE CONTROL
The SISO ARMAX model is given by
A(q
−1
)y
t
= B(q
−1
)u
t
+C(q
−1
)e
t
(37)
where A(q
−1
),B(q
−1
) and C(q
−1
) are polynomials
in the backward shift operator q
−1
, i.e. A(q
−1
) =
1 + a
1
q
−1
+ ... + a
n
q
−n
,B(q
−1
) = b
1
q
−1
+ ... +
b
n
q
−n
,C(q
−1
) = 1 + c
1
q
−1
+ ... + c
n
q
−n
and y
t
is the
output , u
t
is the control input, and {e
t
} is assumed
to be a sequence of independent variables with zero
mean and variance σ
2
e
. Unknown system parameters
θ = (a
1
,...,a
n
,b
1
,...,b
n
,c
1
,...,c
n
)
T
(or corresponding
parameters of δ model) are estimated on-line to ob-
tain an updated model at time t, i.e.
ˆ
θ
t
(or corre-
sponding δ model) which is in turn used for updat-
ing the lqg adaptive control of the system. The pa-
rameter estimates of δ model can be used for tun-
ing the continuous-time LQG/LTR control assuming
the sampling period is small enough. In this way a
continuous-time system identification problem can be
omitted.
ARMAX model (31) has an equivalent innovation
state space representation
x
t+1
= Fx
t
+ gu
t
+ k
p
e
t
(38)
y
t
= h
T
x
t
+ e
t
(39)
where g = (b
1
,...,b
n
)
T
, k
p
= (c
1
− a
1
,...,c
n
−
a
n
)
T
, h
T
= (1,0, ...,0)
F =



−a
1
1 ... 0
. . ... 0
−a
n−1
. ... 1
−a
n
. ... 0



,
k
p
is the stationary gain vector for the associated
Kalman predictor corresponding to (3)
ˆx
t+1/t
= F ˆx
t/t−1
+ gu
t
+ k
p
˜y
p
t
(40)
where ˜y
p
t
= y
t
− h
T
ˆx
t/t−1
and σ
2
˜y,p
is the variance of
˜y
p
t
for which it holds σ
2
˜y,p
= σ
2
e
.
The actual model used for LQG/LTR control signal
u
t
calculation is obtained for current parameter esti-
mates
ˆ
θ
t
.
The investigated problem is to check out how the
approximated δ model used in adaptive LQG/LTR
control can be used in tuning the continuous-time
LQG/LTR control.
The issue of stability of the proposed adaptive
LQG/LTR control system is of course crucial. This
depends on the asymptotic convergence of parameter
estimates, particularly taking into account that in gen-
eral the parameter estimation in LQG adaptive control
even in the lack of modelling error, does not assure
the convergence to the true parameters. Closed loop
stability and good performance cannot be guaranteed
especially during the transient stage.
7 SIMULATIONS
Consider as an example a third-order minimum-
phase actual system obtained by discretizing the
continuous-time system
G(s) =
s+ 5
(s+ 1)(s+ 2)(s+ 3)
=
−s+ 1
(s+ 1)(s+ 2)
+
1
s+ 3
ADAPTIVE LQG CONTROL WITH LOOP TRANSFER RECOVERY
511

with ZOH and sampling period T
s
= 0.5s whose nom-
inal part has a standard state space representation
A =

−3 1
−2 0

, B =

−1
1

, C =

1 0

and which yields the following transfer function in
q
−1
operator
G(q
−1
) =
0.09771q
−1
+ 0.06925q
−2
− 0.005945q
−3
1− 1.198q
−1
+ 0.4406q
−2
− 0.04979q
−3
=
=
−0.1612q
−1
+ 0.2856
−2
1− 0.9744q
−1
+ 0.223
−2
+
0.259
−1
1− 0.223
−1
. (41)
The first part of G(q
−1
) is taken for undermod-
elling. Substituting q
−1
= (1 + δT
s
)
−1
the corre-
sponding discrete-time δ model is obtained as
y
δ
t
+ α
1
y
δ
t−1
+ α
2
y
δ
t−2
= β
1
u
δ
t−1
+ β
2
u
δ
t−2
. (42)
where α
1
=
2+a
1
T
p
, α
2
=
1+a
1
+a
2
T
2
p
, β
1
=
b
1
T
p
, β
2
=
b
1
+b
2
T
2
p
and y
δ
t
=
y
t
−2y
t−1
+y
t−2
T
2
p
, y
δ
t−1
=
y
t−1
−y
t−2
T
p
, y
δ
t−2
= y
t−2
,
u
δ
t−1
=
u
t−1
−u
t−2
T
p
, u
δ
t−2
= u
t−2
.
As already mentioned, in both cases, a second-order
ARX model was taken for identification and cer-
tainty equivalence principle was used to implement
the adaptive control system to demonstrate the robust-
ness of adaptive LQG/LTR controller with respect to
undermodelling. The simulation of continuous -time
adaptive LQG control with LTR and estimation based
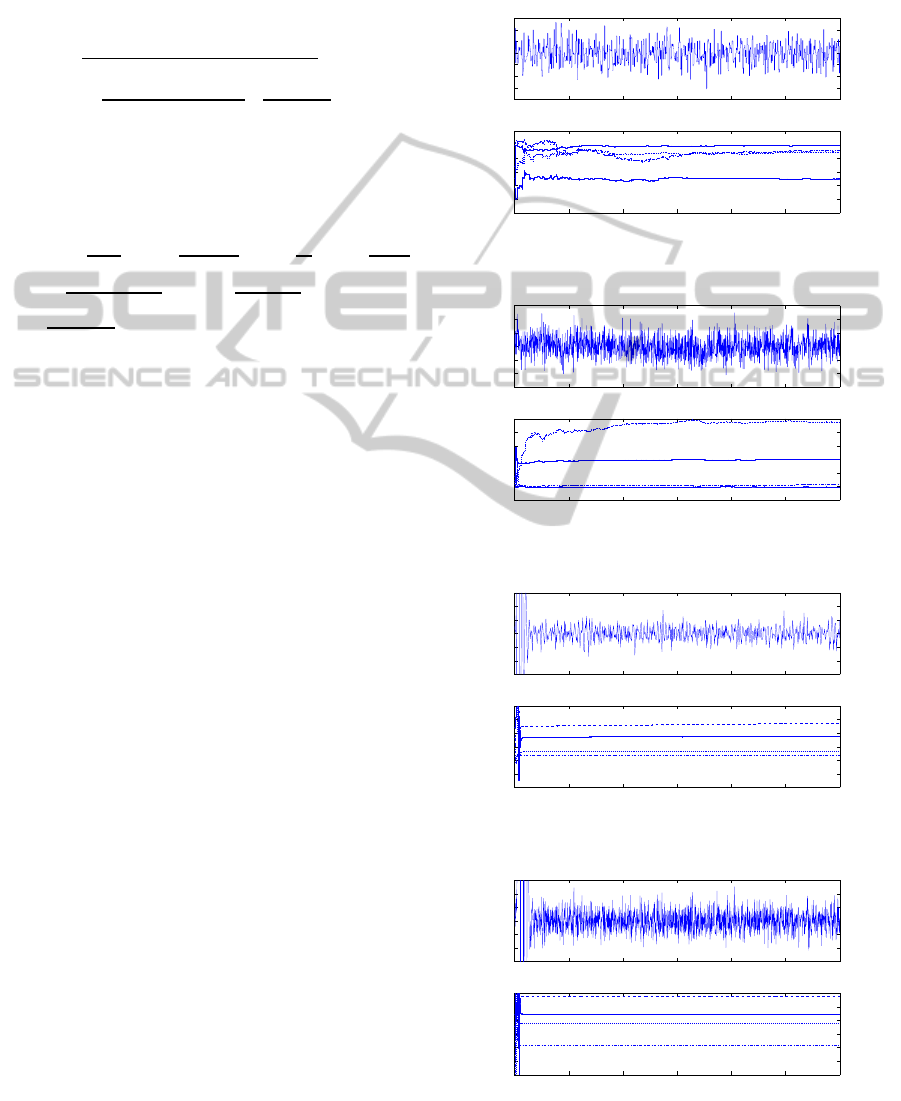
on the δ model are shown in Figs.1,2 for ρ = 0.001
and T
s
= 0.5, 0.2, respectively. An output variance
in steady state was calculated: for the case of Fig.1 it
equals to 0.2090, and for the case of Fig.2 it is 0.6051.
The case with δ model is shown in Figs.3,4
for T
s
= 0.5,0.2, and corresponding variances equal
to 0.2956, 0.5584, respectively. In both cases the
adaptive control system performs well, however the
continuous-time LQG/LTR adaptive control system
with δ model tuning is superior with respect to out-
put variance.
System parameters were identified using the stan-
dard recursive least squares (RLS) algorithm for t =
1,..., 300 and σ
2
e
= 0.1. Obviously, in the general case
of ARMAX model the recursive pseudolinear regres-
sion (RPLR) or recursive prediction error (RPEM) al-
gorithm must be used. It was shown in (Nilsson and
Egardt, 2010), that RPEM is more suitable in the con-
sidered undermodelled situations taking into account
the asymptotic properties of the algorithm.
8 CONCLUSIONS
The problem of using loop transfer recovery for adap-
tive LQG control is presented in both z and γ do-
mains. In the latter case an asymptotic equivalence
(T
s
→ 0) with the continuous-time system is inves-
tigated. Example of third-order actual system de-
scribed by a second-order ARX model is taken for
simulation. Simulation results show an effectivness
of the LTR technique as a method for robustifying the
0 50 100 150 200 250 300
−2
−1.5
−1
−0.5
0
0.5
1
1.5
y(t)
0 50 100 150 200 250 300
−1
0
1
2
3
4
5
θ
t
t
Figure 1: Output signal and estimates for T
s
= 0.5, ρ =
0.001.
0 50 100 150 200 250 300
−3
−2
−1
0
1
2
3
y(t)
0 50 100 150 200 250 300
−5
0
5
10
15
20
25
t
θ
t
Figure 2: Output signal and estimates for T
s
= 0.2, ρ =
0.001.
0 50 100 150 200 250 300
−3
−2
−1
0
1
2
3
y(t)
0 50 100 150 200 250 300
−1
−0.5
0
0.5
1
1.5
2
t
θ
t
Figure 3: Output signals and estimates for T
s
= 0.5, δ
model.
0 50 100 150 200 250 300
−3
−2
−1
0
1
2
3
y(t)
0 50 100 150 200 250 300
−1
−0.5
0
0.5
1
1.5
2
t
y(t)
Figure 4: Output signals and estimates for T
s
= 0.2, δ
model.
ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics
512

adaptive LQG control.
REFERENCES
Athans, M. (1986). A tutorial on the lqg/ltr method. In
Proc. American Control Conf., pages LIDS–P–1542,
Seattle, USA.
Bitmead, R., Gevers, M., and Wertz, V. (1990). Adaptive
Optimal Control. Prentice Hall International.
Krolikowski, A. (1995). Amplitude constrained
adaptive LQG control of first order systems.
Int.J.Adapt.Contr.Sign.Proc., 9(3):285–299.
Kulcsar, B. (2000). Lqg/ltr controller design for an air-
craft model. Periodica Polytechnica, Ser.Transp.Eng.,
28(1-2):131–142.
Maciejowski, J. (1985). Asymptotic recovery for discrete-
time systems. IEEE Trans. Automat. Contr.,
30(6):602–605.
M¨akil¨a, P., Westerlund, T., and Toivonen, H. (1984). Con-
strained linear quadratic gaussian control with process
applications. Automatica, 20(1):15–29.
Nilsson, M. and Egardt, B. (2010). Comparing recursive
estimators in the presence of unmodeled dynamics. In
Proc. IFAC Symp. ALCOSP, pages 135–149, Antalya,
Turkey.
Tadjine, M., M’Saad, M., and Dugard, L. (1994). Discrete-
time compensators with loop transfer recovery. IEEE
Trans. Automat. Contr., 39(6):1259–1262.
Tay, T. and Moore, J. (1991). Adaptive LQG controller with
loop transfer recovery. Int.J.Adapt.Contr.Sign.Proc.,
5(2):135–149.
Tay, T. and More, J. (1989). Loop recovery via h
∞
/h
2
sen-
sitivity recovery. Int.J.Control, 49(4):1249–1271.
ADAPTIVE LQG CONTROL WITH LOOP TRANSFER RECOVERY
513