MOBILE ROBOT

A Complete Framework for 2D-path Planning and Motion Planning

Giuseppe Zuffanti

1,2

and Costantino Scozzafava

Lagrange Project-CRT Foundation, Institute for Scientiﬁc Interchange Foundation, 10133 Turin, Italy

Department of Computer Science, University of Turin, Turin, Italy

Erxa S.r.l., 10149 Turin, Italy

Keywords:

Path planning, Motion planning, Roadmap graph, Potential ﬁeld, Look-ahead, Obstacle avoidance, Attraction

point, Dynamic environment.

Abstract:

In this work we focus on the problem of 2D path planning and motion planning for a mobile robot. The

goodness of a path planning and motion planning methods can be evaluated primarily through the parameters

such as safety of generated trajectory speeds and robustness against dynamic changes of the environment. In

all applications that use mobile robots, the motion planning problem is of crucial importance. According to

different applications one can put emphasis on the previous characteristics listed, potentially to the detriment

of the others. Typically, methods that generate high trajectory speeds for the navigating robot appears to be

less robust and safe. The importance that the path planning and the motion planning problem play in practical

applications is also demonstrated by the several techniques developed to tackle them. We propose a complete

framework which creates a clear shortest path for a robot in an environment with static obstacles and generates,

in real time, the accurate trajectory taking into account the presence of dynamics obstacles. Application of the

framework to the case of a differential drive robot in a dynamic indoor environment is shown and the proposed

approach has been tested both with simulation and real data.

1 INTRODUCTION

One of the main tasks of a wheeled mobile robot

(WMR) is the capability of plan and execute collision-

free paths when moving around (Budanov and De-

vyanin, 2003). While the problem of path planning

has been historically addressed as a purely geometric

issue (since the piano-mover problem), in the case of

a real robot moving in its surroundings several new

constraints have to be considered and added to the

original problem position (Canny, 1988), (Latombe,

1991), (LaValle, 2006). Typical such constraints arise

when taking into account the anholonomy of the robot

kinematics model, dynamic changes in the surround-

ings and uncertainties related to the sensors measure-

ments (Siciliano et al., 2008). In this work we de-

scribe a framework for the solution of the path plan-

ning of a WMR in which the main problem is di-

vided in two sub-problems: 1) planning of a geomet-

ric, collision-free, motion and 2) execution of the mo-

tion in a dynamic scenario. Finally further dynamical

constraints on the generated trajectories are imposed

to let the motions be generated at the maximum allo-

wed speed taking into account the safety of both the

robot it-self and the surrounding objects (LaValle and

Kuffner, 1999).

The proposed solution has been implemented and

tested using a robotic platform Pioneer P3DX and

a proprietary real-time control software system (RT-

Platform).

2 PATH PLANNING FOR

DYNAMIC ENVIRONMENT

Nevertheless, in most cases, moving directly to the

goal isn’t possible due primarily to the structure of the

surroundings. Besides, also if the problem of deter-

mining a feasible way to the goal is solved, one must

take into account that unexpected dynamic obstacles

can cross the robot trajectory. In an indoor scenario

these problems can be directly related to moving to

some room in an ofﬁce (or a house) and avoiding col-

lisions with persons and with not previously known

objects (chairs, moving people, etc.). Such a kind of

417

Zuffanti G. and Scozzafava C..

MOBILE ROBOT - A Complete Framework for 2D-path Planning and Motion Planning.

DOI: 10.5220/0003648504170426

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (MORAS-2011), pages 417-426

ISBN: 978-989-8425-75-1

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

scenario (non-structured, partially dynamic) will be,

for the rest of the document, the reference scenario in

which hypotheses and experiments have their validity.

Accordingly to the problem decomposition we

identiﬁed two main functional modules able to cope

with the given sub-problems. They are the Path Plan-

ner OFF-Line Module and the Path Planner ON-Line

Module.

2.1 Path Planner OFF-line Module

An important inﬂuence on the quality of the path

founded by the Path Planner OFF-Line Module, is the

quality of the graph that represents the free space. For

to represent the free space and for to build the cor-

responding graph we have studied the map building

techniques present in literature (Veeck and Burgard,

2004), (Masehian and Movafaghpour, 2009). All of

them use the information from the on-board sensors

of the robot. In the map building process it’s possible

to identify two main phases:

1. acquiring information through sensors about the

characteristics of environment and objects sur-

rounding the robot;

2. processing this information to obtain a summary

of the space around the robot, discarding the in-

consistent information due to the uncertainty and

imprecision of sensors.

There are many possible solutions to accomplish

these two steps and to get maps, but those the most

often and successfully used are based on grid maps,

on topological maps or on geometrical maps.

We developed a speciﬁc Geometric Map Build-

ing algorithm (GMB) capable of building, in a dy-

namically and incrementally approach, a geometric

map of the environment using sonar range or laser

scanner. The global map is composed of two main

type of contours, the ﬁrst set of contours represents

the whole free space while the second set represents

the entire holes contours. We preferred the geomet-

ric map representation because we have a low mem-

ory occupancy, especially in situations where is very

broad. This choice is also useful because is better

to adapt representation of the points constituting the

map if necessary corrections due to errors caused by

the detection system of the robot, through its analyt-

ical operations of vector geometry. Starting from a

result of the dedicated map building module which

represents the 2D environment, a ﬁrst goal was to ap-

ply a mesh algorithm to obtain a triangulation of free-

space.

Speciﬁcally, a standard 2D mesh geometry rep-

resentation is used for depicting an hypothetical en-

vironment map using as input the result of the map

building module. This is the potentially viable areas

by the robot. In general the term mesh refers to a set

of polygons such that two of its elements do not inter-

sect, or share a vertex, or an edge. Each polygon ap-

proximates a portion of the surface. Meshes are easy

to represent, to manipulate, to display and are also re-

constructed from irregularly sampled data. In particu-

lar we have chosen the triangular mesh, for which in-

ternal representation we stored geometric information

such as the position of the vertices of triangles, the

connectivity and the relationships between triangles

themselves. The used mesh algorithm can produce a

Constrained Delaunay Triangulation (CDT) (Delau-

nay, 1934): a construction of grids with ﬁnite trian-

gular element on plans domain ﬁlling generic forms.

The triangulation mesh algorithm is an exact decom-

position method of the free-space that produce a col-

lection of non-overlapping cells (triangles) and the

union of these, exactly equals the free-space or rather

the space in R2 where the robot can move without

colliding by static obstacles.

To get a free-path to move the robot from a start to

a goal is to keep it moving only over triangles that rep-

resent the free-space, or the part of the environment

completely devoid of obstacles (Lien et al., 2003). It

was thought to obtain a free-path as follows:

1. generate a basic Roadmap, always available in the

data structure, representing the undirected graph

G = (V , E ) where V is the set of all centroids of

the triangles forming the mesh in the free-space,

E is the set of all edges that connect each node V

with all adjacent nodes (minimum one and maxi-

mum three adjacent nodes for each triangle)

2. starting from a roadmap graph, a start point and

a goal point belonging to the free-space, on the

roadmap graph it is built, with Dijkstra algorithm,

a MST(Minimum Spanning Tree) or minimum

weight spanning tree. The graph is weighted by

the length of each edges of the graph. The MST

has as its root the centroid of the triangle closer to

the start point of the robot position.

3. if we denote by C

the centroid of the triangle in

the free-space closer to the start point and with C

the centroid of the triangle in the free-space closer

to the point of goals, we may deﬁne the Shortest-

Path (SP) as the path in the roadmap graph joining

and C

plus two edges, one that connects the

start with C

and one that connects C

with the

goal. This path represent a safety shortest path in a

free space that the Path Planner ON-Line Module

will use to planned a safe and smooth trajectory.

To ensure the MST covers the free-space really navi-

gable by the robot, a further prune operation is made

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

418

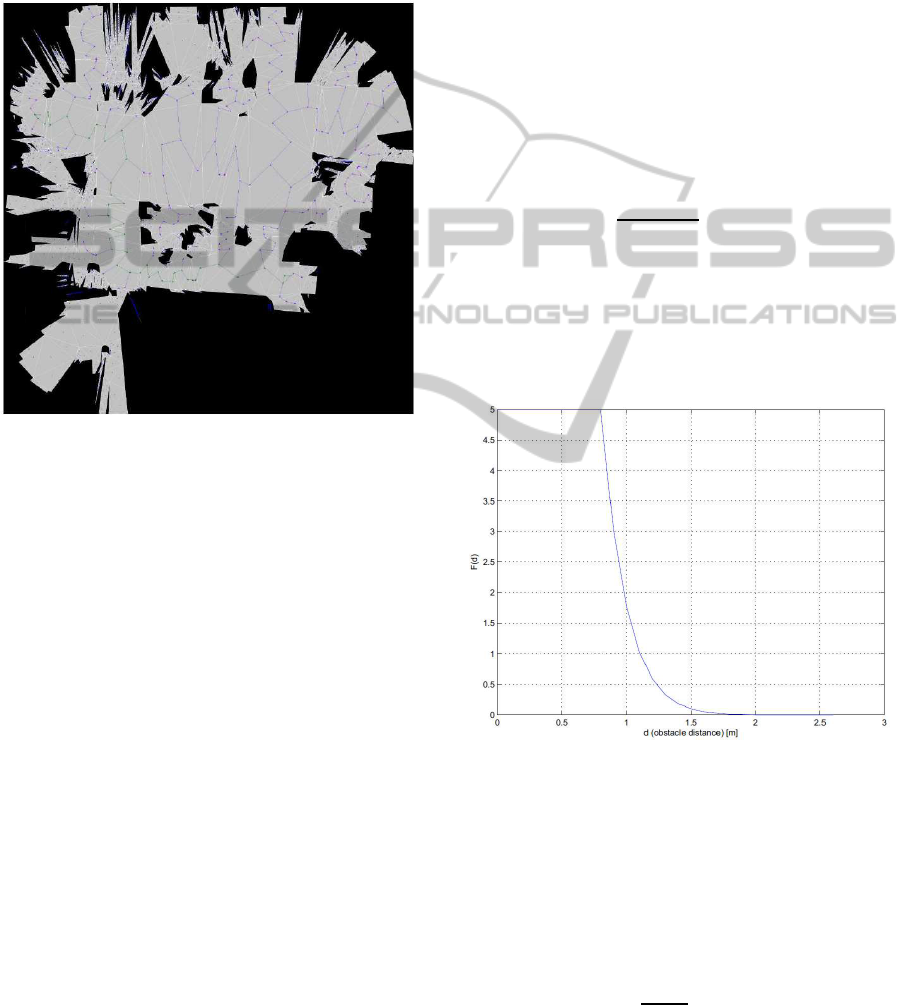
in the MST building phase to leave out the nodes of

the graph that represents all the centroids of a trian-

gles mesh where the robot can not enter because of

their size. Fig.1 illustrates an example of a Pruned

Minimum Spanning Tree (PMST) built on a roadmap

graph which covers a large portion of the free space

in a real indoor environment.

Figure 1: In the bottom left area of the picture one can ob-

serve the result of the graph-edges pruning (corridor is nar-

rower than the size of the robot).

2.2 Path Planner ON-Line Module

The Path Planner OFF-Line Module allows to obtain

a set-point, or rather the list of the triangles centroids

provided by shortest-path algorithm, which are useful

as reference for the robot to move in safe areas, free

of static obstacles. The Path Planner ON-Line is the

module phase that implement all those algorithms ca-

pable of managing the proper handling of the robot

and the obstacle avoidance in case of mobile or un-

expected obstacles. This is the stage where it should

consider the dynamic characteristics of a real envi-

ronment (moving obstacles, local changes of the map

built during off-line phase, etc...), and then the reason-

ing capabilities and the reactive abilities of the mobile

robot. To manage the robot movements an interpola-

tion strategy between the current robot position and

the goal position has been tested, to generate trajecto-

ries keeping the mobile robot’s kinematic constraints.

We have chosen to exploit the concept of Attraction

Points (Geraerts and Overmars, 2007), a very typical

approach in the potential ﬁeld methods, as follows:

the robot is attracted by an appropriate node of SP at

a time, and when this target is no longer valid an op-

portune target node is activated. Once all centroids of

the SP have been activated the robot it is performed a

last move toward the point of ultimate goal.

The problem of obstacle avoidance has been faced

using the potential ﬁeld method. The function that de-

scribes this ﬁeld is generally the sum of distinct com-

ponents depending on attractive and repulsive forces

(Rimon and Koditschek, 1992). The global motions

of the robot is mainly guided by a dynamically attrac-

tion point that represent the principal oracle to follow

to ﬁnd the safe way to identify the best way to goal.

The attraction point attracts the robot with force F

Let x be the current robot position, p(x) be the op-

portune node position of PP, d be the Euclidean dis-

tance between x and p(x), b be the sensor beam.

The F

is deﬁned as:

(x− p(x))

· min(d, b). (1)

A repulsive force F

is generated by dynamic local

obstacles or rather the obstacles in the environment

around to the robot that there did not exist or were far

when the SP is created. A repulsive force deﬂection

determines the behaviour that the robot must take

each obstacle is detected (Fig.2).

Figure 2: Repulsive force deﬂection.

Let d

be the Euclidean distance between robot po-

sition x and o

(a point corresponding to a sensor ob-

stacle measure), s be the size robot, F

sat

be the repul-

sive force saturation, D

be the Euclidean distance

between x and o

to reset F

, n be the shape of F

The F(d

) is deﬁned as:

F(d

) =











sat

if d

< s

sat



−D

s−D



if s ≤ d

≤ D

0 if d

> D

(2)

MOBILE ROBOT - A Complete Framework for 2D-path Planning and Motion Planning

419

(a) Safe trajectory (Not optimized). (b) Safe and optimized trajectory by

lookahead.

cles.

(d) Modiﬁed trajectory caused by unex-

pected local dynamics obstacles.

Figure 3: Examples of different trajectory in a simulate world.

Let m be the number of surround obstacles measured

by o

, y

be the position of surround obstacles at o

distance, d

be the Euclidean distance between robot

position x and o

The F

is deﬁned as follows:

= −

∑

i=1

− x

· F(d

). (3)

The ﬁnal force F is calculated as:

F = F

+ F

. (4)

By calculating the ﬁnal force F we can get the op-

portune sub-target in the free-space that the Motion

Planning module may use to calculate the trajectory

of the robot respecting kinematic constraints (Chitsaz

et al., 2006). Additional strategies to smooth trajec-

tories have been studied and implemented to reduce

redundant paths and robot acceleration/deceleration

phases. This was possible introducing an appropri-

ate look-ahead feature (Fig.4) allowing the Path Plan-

ner ON-Line Module to use as main attraction point

a proportionally point onto the edge between the next

two centroids of the SP.

The new target is calculated as follows:

LookAheadON ← near(P

, T

)

if LookAheadON = true then

← α

k+2

− T

k+1

)

else

← T

end if

where,

= robot pose,

= current target,

= centroid of k-th triangle,

k+1

= centroid of (k+1)-th triangle,

k+2

= centroid of (k+2)-th triangle,

α = percentage parameter,

= Euclidean distance between T

k+1

and T

= Euclidean distance between T

k+2

and

k+1

Figure 4: Example of look-ahead technique.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

420

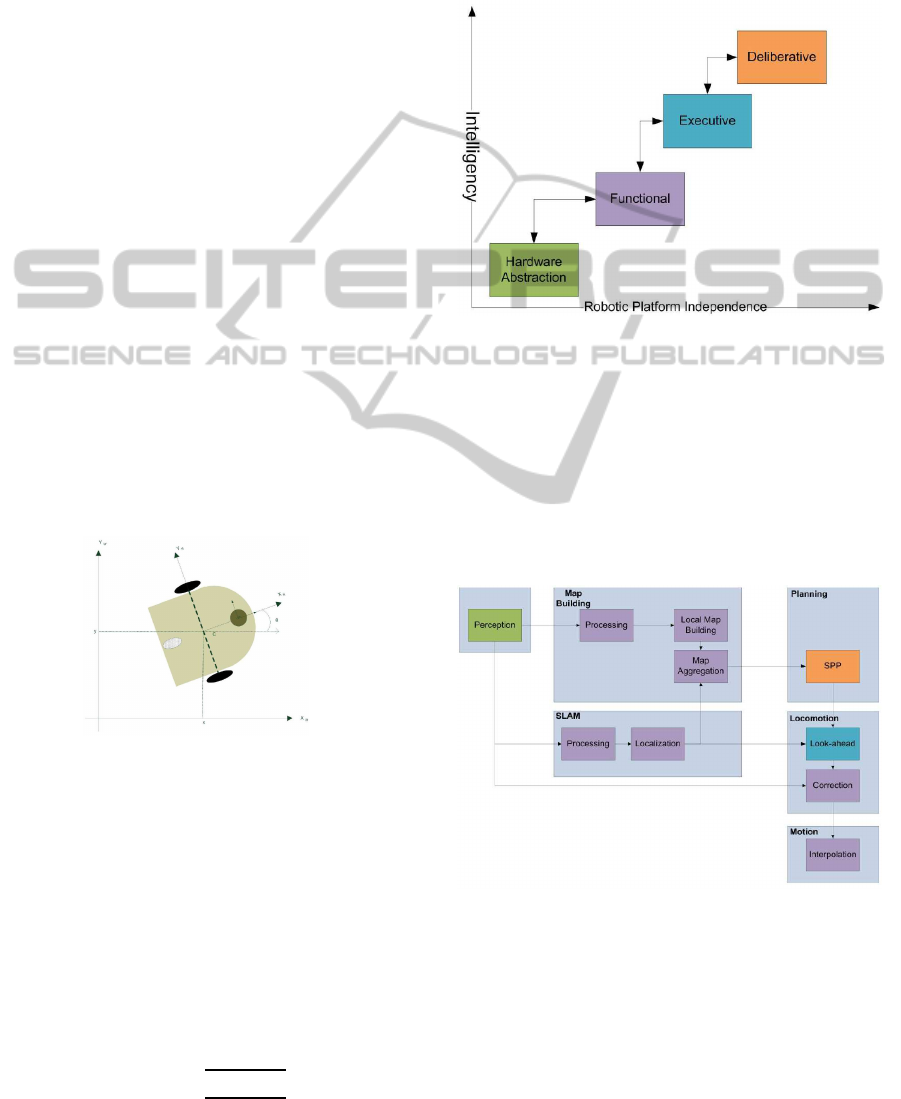
Fig.3(a), Fig.3(b) illustrates two different types of

trajectory of the robot obtained with different tech-

nique in a simulate world (box size:40x40 [m]). The

ﬁrst simulative results showed that the robot, in a cer-

tain narrow area of the map, could not divert its tra-

jectory in time because of speed. To work around

the problem we introduced a feed-rate control speed

that proportionally modify the speed parameter of

the robot in function of nearest obstacles surround in

agreement with the max speed parameter and max ac-

celeration parameter of the robot. An opportune value

saturation is applied to prevent instable and unsafe sit-

uations. Fig.3(c), Fig.3(d) illustrates an example of

the reactivity of the Path Planner ON-Line Module

(box size:10x10 [m]).

3 THE ROBOT AND ITS

SOFTWARE CONTROL

ARCHITECTURE

In order to test the proposed solution a real-time soft-

ware platform (RT-Platform) has been designed and

developed to control a mobile robot (Pioneer P3DX).

The robot has been equipped with an external laser

range scanner (Sick LMS 100) and a Acer-One net-

book executing the control software algorithms on a

XP tailored OS.

Figure 5: Robot kinematic model.

The robot kinematic model (Fig. 5) used for mo-

tion interpolation is based on the simpler model given

by the following equation:





˙x(t)

˙y(t)

θ(t)









υ(t)cos(θ(t))

υ(t)sin(θ(t))

ω(t)





(5)

where υ(t) and ω(t) represent, respectively, the linear

and angular velocities of the robot body ﬁxed frame

deﬁned as:



υ(t)

ω(t)



(t)+ω

(t)

(t)−ω

(t)

(6)

where,

(t) = angular speed of the right wheel,

(t) = angular speed of the left wheel,

R = wheel radius (before calibration),

D = wheel centers distance.

Figure 6: Functional, abstract layers of the proposed archi-

tecture.

Our proposed architecture is based on (Alami et al.,

1998). It can be decomposed in four layers: a delib-

erative level, an executive level, a functional level and

an hardware abstraction (Fig.6).

In the previous layered scheme the data ﬂowing

through path planning modules is summarized in

Fig.7.

Figure 7: Data ﬂows and transformations along the path

planning ’toolchain’. The color of each block refers to the

architectural functional layer it belongs.

3.1 Data Perception

The Perception module collects the laser raw data at

a frequency of 2Hz and stores them in a real-time

database. It then signals to all interested modules that

MOBILE ROBOT - A Complete Framework for 2D-path Planning and Motion Planning

421

fresh data are ready in the database. A timestamp

is coupled to every newly acquired set of data. The

mobile robot P3DX (Fig.8) has been equipped with

a SICK LMS-100 Laser Scanner mounted on the top

of the robot. The LMS-100 laser scanner has been

conﬁgured to collect range measurement over a 270

◦

range, with 0.25

◦

of angular resolution. Moreover the

scanning plane of the LMS-100 has been positioned at

an elevation, from the ﬂoor, of around 35cm. Due to

the short range measured in an indoor environment, at

this stage of the work, no calibration of the sensor ori-

entation with respect the parallelism to the ﬂoor was

made; while the mounting offset with respect of the

body-ﬁxed frame F

of the robot was estimated to be

at around [0.20] meters (Fig.5).

Finally we integrated a software driver for the sen-

sor in the RT-Platform architecture through a USB-to-

serial connection. The software driver provides raw

data measured by the sensor to all subscribed soft-

ware components leaving the choice of how to pro-

cess them to each component.

Figure 8: Pioneer P3DX.

3.2 Data Processing

SLAM Function. The raw data stored in real-time

database are processed in order to extract corner and

line features eligible to become new or yet known

landmarks to be entered in the Update phase of the

SLAM algorithm.

Map Building Function. The raw data stored in real-

time database are processed in order to build a local

map of the surroundings.

3.3 Local Map Aggregation and

Planning

After a Local Map has been built it’s fused in a Global

Map. The fusion, or aggregation, operation is per-

formed taking into account the estimated robot posi-

tion (SLAM) and the yet existing landmarks. Once

the Global Map has been updated it’s possible for the

Path Planning OFF-Line Module to deliberate a suit-

able path to a goal position. The path is the input for

the Locomotion Module.

3.4 Locomotion

The path generated by the Path Planner OFF-Line

Module is the input for the Locomotion Module (Al-

bagul and Wahyudi, 2004). It will provides two main

functionalities:

1. trajectory smoothing via a spatial look-ahead;

(Liang and Liu, 2004)

2. dynamic obstacle detection.

Look-ahead. The look-ahead sub-function, ac-

cordingly to dynamic obstacle detection, is able

to shorten and smooth the route to the ﬁnal goal

by foreseeing which targets of the original path

have to be reached and at which instant in time the

current target can be replaced by its successor (Fig.9).

Figure 9: The green circles, representing the intermediate

targets ofa path, are used to smooth the generated trajectory.

Obstacle Detection. Detecting dynamic obstacle

while moving along a path is a fundamental function

both for robot safety and goal effective reachability.

The laser raw data are processed in order to measure

the reachability of the current and next targets. The

information is 1) propagated to the look-ahead func-

tion and 2) used to correct the robot speeds in order to

have always enough space for to brake.

3.5 Motion Interpolation

The Motion Interpolation module has in charge the

goal of to generate speed targets for the Pioneer P3DX

robotics platform at a frequency of 10 Hz. Given

the kinematics model in equation 5, it has been re-

visited providing a special choice for the system state

equations as shown in (Aicardi et al., 1994). Then a

state-dependent, smooth, non-linear control law gen-

erating the command vector [υ, ω]

has been proven

to drive the robot in the desired ﬁnal position and ori-

entation. The closed loop chain generating the speed

commands for the robot is shown in Fig.10.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

422

Figure 10: Closed loop control schema.

4 RESULTS

The simulative and experimental results show the ef-

fectiveness of the approach. The Locomotion module

has been made robust in case of replanning because

the high level system autonomously reconﬁgures it-

self to correctly achieve the mission. The implemen-

tation of the all module in a variety of dynamic indoor

environment shows the efﬁciency of the approach as

a good navigation framework for a mobile robot.

The simulative and experimental results have

shown the effectiveness of the proposed approach.

Firstly, experimental test-cases have been built in or-

der to test the behavior of every speciﬁc module (Path

Planner OFF-Line Module only, Path Planner ON-

Line Module only); then the complete planning and

control chain has been closed in order to let the robot

(Pioneer P3DX Fig.8) plan and navigate in an un-

structured indoor scenario. In Fig.11(a) are shown

both the real trajectory of the robot under the in-

ﬂuence of modiﬁcations induced by the look-ahead

strategies and the decrease of trajectory duration in

time (Fig.11(b)) due to the elimination of intermedi-

ate targets.

To verify the look-ahead improvements of the

generated trajectories we performed 50 runnings of

the robot over 5 different path sets; all paths were

generated inside the Erxa s.r.l. ofﬁce letting the robot

moves from one room to another. Moreover between

paths of the same set were slight differences due to the

variable presence of chairs or baskets. For each set of

paths the average time and length of the trajectories

execution has been evaluated. The results are shown

in Table1, where, for each column, one can observe

the average lengths and average times with and with-

out the Look-ahead functionality working. For each

paths set an increase of performances for both length

and time has been evaluated as the percent ratio of the

cases without Look-ahead over the cases with Look-

ahead. The same trajectory has then been executed

by introducing, along the robot motion, a number of

dynamic obstacles as shown in Fig.12(c) (red dots)

to demonstrate the capability of obstacle avoidance

via the local trajectory deformation; the obstacles, de-

tected at run-time, are used to smoothly modify the

local targets to the robot.

The resulting behavior allowed the robot to au-

tonomously move in a scenario where people was

moving around. Furthermore, in order to improve

the safety of the people and of the robot it-self, a

proximity detection alert functionality based on sonar

range readings has been implemented to eliminate the

risk of collision against high-speed moving objects; in

fact in this cases the relatively low frequency of laser

range readings update could result in unseeing some

quickly moving obstacle.

(a) The comparison of two trajecto-

ries with and without look-ahead.

(b) The performance of look-ahead.

Figure 11: Results of different trajectory in a static real

world.

MOBILE ROBOT - A Complete Framework for 2D-path Planning and Motion Planning

423

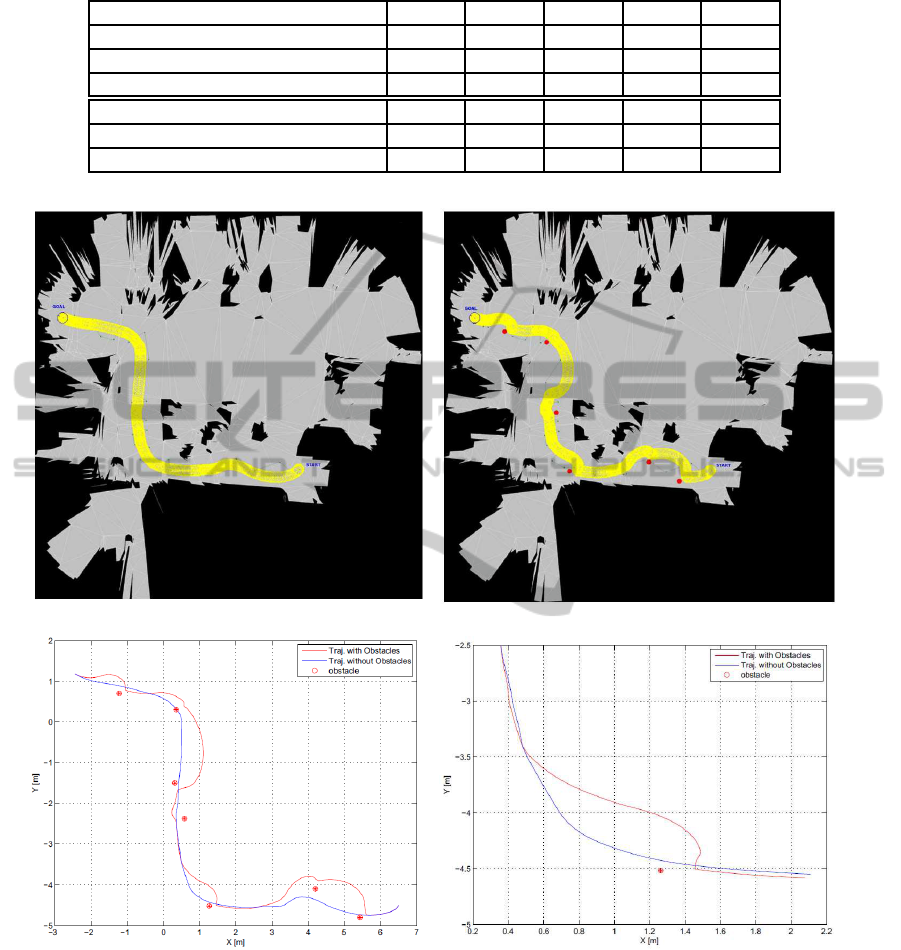
Table 1: A comparison between trajectory lengths and execution times with and without look-ahead functionality active on

the Pioneer P3DX moving in Erxa ofﬁce. The percentages are the ratios between the obtained results in two cases.

Path1 Path2 Path3 Path4 Path5

Traj.Lenght With Look-Ahead [m] 13.975 21.223 19.214 28.347 24.231

Traj.Lenght Standard [m] 15.129 23.214 20.146 32.421 27.215

Performance[%] 7.63 8.58 4.63 12.57 10.96

Traj.Time With Look-Ahead [s] 12.536 18.949 17.216 23.622 21.405

Traj.Time Standard [s] 30.128 45.517 38.742 62.953 51.349

Performance[%] 58.39 58.37 55.56 62.48 58.31

(a) A true trajectory in a real static environment. (b) The newtrajectory caused by unexpected local dynamics obstacles.

Figure 12: Results of different trajectory in a static and dynamic real indoor environment.

5 CONCLUSIONS

In this work we have shown how the path planning

problem for a wheeled mobile robot can be decou-

pled in two sub-problems: a problem related to the

geometric, collision-free, path search and a problem

related to the path execution in a dynamic world. Both

the solutions rely on the use of laser sensors; the ﬁrst

for building a static map of the surroundings, while

the second for avoiding dynamic changes of the sur-

roundings it-self. Then the validity of the solution has

been demonstrated by its implementation in a soft-

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

424

(a) A true trajectory in another real static environment. (b) The newtrajectory caused by unexpected local dynamics obstacles.

Figure 13: Results of different trajectory in another static and dynamic real indoor environment.

ware control architecture for a wheeled mobile robot.

Because the collision-free path generation is based on

a self-built map that is constantly updated by new per-

ceived measures, no pre-conﬁgured maps of the sur-

roundings are needed.

Finally the functional and operational decoupling

of the solutions gives the possibility to study, de-

velop and test different strategies for each of the sub-

problems. Furthermore we deployed other algorithms

that are not present on this work that allowed to cou-

ple our PP module and MP module with a control

loop involving simultaneous localization and map-

ping. The performed experimentations within a real

dynamic environment of these extensions have given

good result in terms of safety, speed, path shortness,

smooth trajectory and reactivity.

Interesting topics for future researches and future

goals are a 1) closer integration of path planning mod-

ules with SLAM and Navigation functions, and 2) de-

veloping a software framework for fully autonomous

exploration and navigation of unstructured worlds.

MOBILE ROBOT - A Complete Framework for 2D-path Planning and Motion Planning

425

ACKNOWLEDGEMENTS

This research has been funded by the Lagrange

Project (fostered and supported by CRT Foundation

and ISI Foundation) and the Erxa S.r.l.. The scientiﬁc

supervision is partly of the Department of Computer

Science, University of Turin.

REFERENCES

Aicardi, M., Casalino, G., Balestrino, A., and Bicchi, A.

(1994). Closed loop smooth steering of unicycle-like

vehicles. In Decision and Control, 1994., Proceed-

ings of the 33rd IEEE Conference on, volume 3, pages

2455 –2458.

Alami, R., Chatila, R., Fleury, S., Ghallab, M., and Ingrand,

F. (1998). An architecture for autonomy. International

Journal of Robotics Research, 17:315–337.

Albagul, A. and Wahyudi (2004). Dynamic modeling and

adaptive traction control for mobile robots. In Indus-

trial Electronics Society, 2004. IECON 2004. 30th An-

nual Conference of IEEE, volume 1, pages 614 – 620.

Budanov, V. M. and Devyanin, Y. A. (2003). The motion of

wheeled robots. Journal of Applied Mathematics and

Mechanics, 67(2):215 – 225.

Canny, J. F. (1988). The Complexity of Robot Motion Plan-

ning. MIT Press, Cambridge, MA.

Chitsaz, H., LaValle, S. M., Balkcom, D. J., and Mason,

M. T. (2006). Minimum wheel-rotation paths for

differential-drive mobile robots. In Proceedings IEEE

International Conference on Robotics and Automa-

tion.

Delaunay, B. N. (1934). Sur la sphre vide. Bulletin of

Academy of Sciences of the USSR, 6:793800.

Geraerts, R. and Overmars, M. H. (2007). The corridor map

method: Realtime high-quality path-planning. In Pro-

ceeding IEEE International Conference on Robotics

and Automation, page 10231028.

Latombe, J. C. (1991). Robot Motion Planning. Kluwer,

Boston, MA.

LaValle, S. M. (2006). Planning Algorithms. Cambridge

University Press, Cambridge, UK, 1st edition.

LaValle, S. M. and Kuffner, J. J. (1999). Randomized kino-

dynamic planning. In Proceedings IEEE International

Conference on Robotics and Automation, page 73479.

Liang, T. C. and Liu, J.-S. (2004). A bounded-curvature

shortest path generation method for car-like mobile

robot using cubic spiral. In Proceedings IEEE/RSJ

In- ternational Conference on Intelligent Robots and

Sys- tems, page 28192824.

Lien, J.-M., Thomas, S. L., and Amato, N. M. (2003). A

general framework for sampling on the medial axis

of the free space. In Proceedings IEEE Interna-

tional Conference on Robotics and Automation, page

44394444.

Masehian, E. and Movafaghpour, M. A. (2009). An adap-

tive sequential clustering algorithm for generating

poly-line maps from range data scan in mobile robot

explorationby. In International Conference on Au-

tomation Technology.

Rimon, E. and Koditschek, D. E. (1992). Exact Robot Nav-

igation Using Artiﬁcial Potential Fields. IEEE Trans.

Robot. & Autom., 8(5):501–518.

Siciliano, B., Sciavicco, L., Villani, L., and Oriolo, G.

(2008). Robotics: Modelling, Planning and Control.

Springer Publishing Company, Incorporated.

Veeck, M. and Burgard, W. (2004). Learning polyline maps

from range scan data acquired with mobile robots.

In International Conference on Intelligent Robots and

Systems.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

426