MANUFACTURING SIMULATION OF BEVEL GEAR CUTTING

Simulation based Approach for Tool Wear Analysis

Christian Brecher

, Fritz Klocke

Christof Gorgels

and Ario Hardjosuwito

Chair of Machine Tools, RWTH Aachen University, Steinbachstr. 19, D-52070 Aachen, Germany

Chair of Manufacturing Technology, RWTH Aachen University, Steinbachstr. 19, D-52070 Aachen, Germany

Keywords: Manufacturing Simulation, 3D Modelling, Gear Cutting Process, Tool Wear Analysis.

Abstract: The transmission of torque or speed from one axle to a non parallel orthogonal axle is realised by bevel

gears. Bevel gears are applied in helicopters, in marine, in rear axles of automotives and industrial drives.

The manufacturing of bevel gears is generally performed in a complex CNC cutting process. Due to

unpredictable tool wear in bevel gear cutting, unexpected production stops e.g. for tool changes occur. This

leads to additional manufacturing costs. Currently it is not possible to analyse the bevel gear cutting process

sufficiently, because of its complexity. Hence, the design of the cutting process happens iteratively in order

to find the best process parameters for a high productivity and optimal tool wear. Thus, an exact knowledge

of the tool wear behaviour is necessary. Hence, a manufacturing simulation for bevel gear cutting has been

developed at WZL. This simulation enables a detailed analysis of the process and consequently of the tool

wear. Within this report a new approach for the tool wear analysis is presented. Four different gear cutting

processes have been analysed regarding tool wear. The introduced new characteristic value K

, which is

calculated by the simulation, has been compared to tool wear from cutting trials. All the presented

investigations will be considered in a simulation-based tool life prediction model which will be developed

within a project funded by the German Research Foundation (DFG).

1 INTRODUCTION

The transmission of torque or speed from one axle to

a non parallel orthogonal axle is generally realised

by bevel gears. Bevel gears are applied in

helicopters, in marine, in rear axles of automotives

and industrial drives as shown in figure 1.

Source: BMW, ZF

Pinion

Ring Gear

Pinion

Ring Gear

Bevel Gears

Figure 1: Exemplary automotive application of bevel

gears.

The manufacturing of bevel gears is generally

performed in a complex Computerized Numerical

Control (CNC) cutting process.

Due to unpredictable tool wear and sudden

failure of the cutting tools, unexpected production

stops for tool changes occur and leads to a loss of

productivity and hence to additional manufacturing

costs. Thus, the productivity of the machining

process depends significantly on the tool wear and

tool life, see Chavoshi (2011). Currently it is not

possible to analyse the bevel gear cutting process

sufficiently, because of its complexity. Hence, the

design of the cutting process happens iteratively in

order to find the optimal process parameters. So an

exact knowledge about the tool wear behaviour is

necessary. These challenges and issues are presented

in figure 2.

Tool WearManufacturing Process



Complex Process Kinematics

– Plunging Process

– Generating Process



Different Tool Concepts



High Local Tool Wear



Critical Wear Behaviour



Low Process Stability

Production Stops

(e.g. Tool Changes)

Iterative Process Design

(trial-and-error)

Source: KlingelnbergSource: Klingelnberg

Figure 2: Challenges in bevel gear cutting.

513

Brecher C., Klocke F., Gorgels C. and Hardjosuwito A. (2011).

MANUFACTURING SIMULATION OF BEVEL GEAR CUTTING - Simulation based Approach for Tool Wear Analysis.

In Proceedings of 1st International Conference on Simulation and Modeling Methodologies, Technologies and Applications, pages 513-520

DOI: 10.5220/0003648605130520

 SciTePress

In order to provide a simulation tool for

analysing and optimising the bevel gear cutting

process a manufacturing simulation has been

developed at WZL, as presented by Brecher (2010)

and Rütjes (2010).

2 MODELLING AND

SIMULATION METHOD

Within the manufacturing simulation a geometrical

penetration is conducted as described by Klocke

(2009), Rütjes (2010) and Brecher (2010). Before

starting the calculation the workpiece, tool and

kinematics have to be modelled.

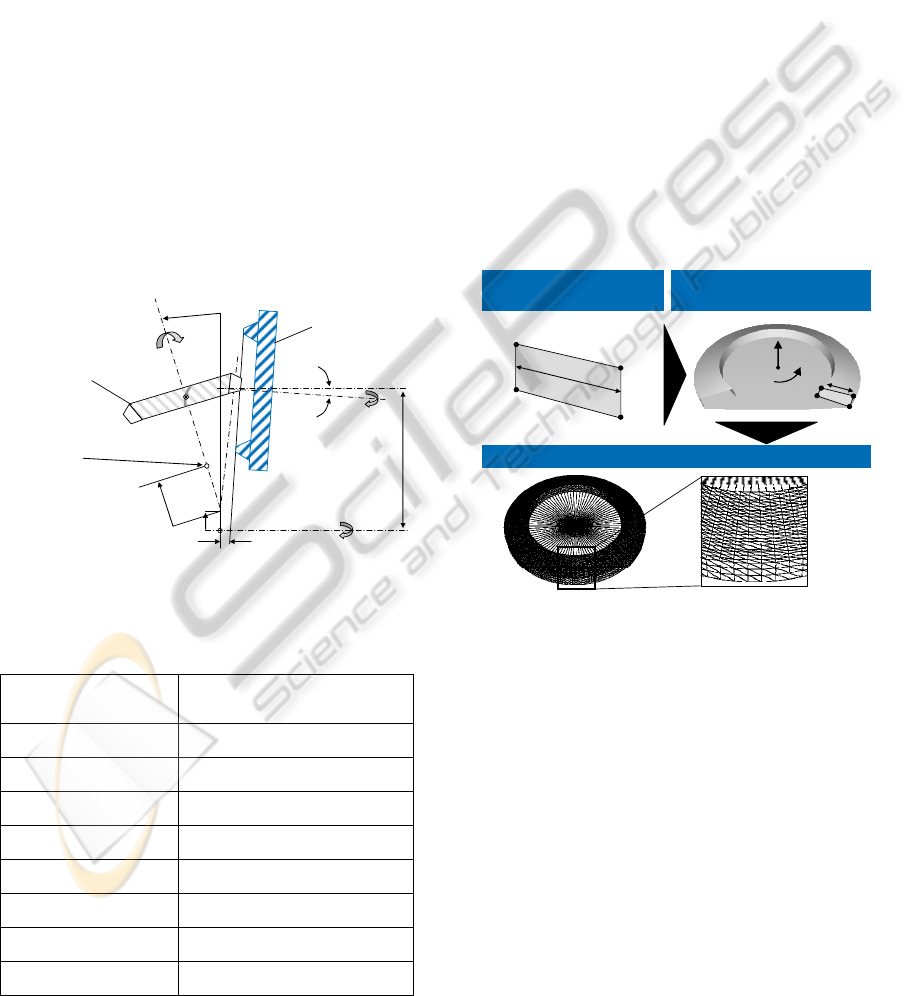
At first the process kinematics are set. The

kinematics of the bevel gear cutting process is

presented in figure 3. Up to 6 CNC axis, like in the

real cutting process, can be considered in the

simulation. In figure 2 and table 1 the axis

movements and positions of the bevel gear cutting

machine are presented.

mccp

Theoretical

Cross Axis

Point of Gear

Cutter Head

Workpiece

Figure 2: Scheme and axis movements of a bevel gear

cutting machine.

Table 1: Axis movements of the cutting machine.

Mccp

Machine center to cross axis

point

Cradle Angle

Modified Roll

Angular Motion

Radial Motion

Horizontal Motion

Vertical Motion

Helical Motion

Tool Rotation omega

For example the axis movement for the depth

position χ of the tool during the cutting process is

calculated by formula 1:

= a

+ b

⋅

(

–

) + c

⋅

(α–α

)

+ d

⋅(α–α

)

+ e

⋅(α–α

)

+ f

⋅(α–α

)

+ g

⋅(α–α

)

+ p

⋅(ω–ω

) + q

⋅(ω–ω

)

⋅(ω–ω

)

+ s

⋅(ω–ω

)

+ t

⋅(ω–ω

)

⋅(ω–ω

)

(1)

Here a series expansion up to the sixth order is

realised for the mean cradle angle α

. The variables

to u

represent the coefficients. E.g. the coefficient

is a constant value therefore a positioning of the

cutter, whereas b

is linear depending on the mean

angle α

which is time-dependent.

In the simulation the workpiece and the tool

envelope are modelled as 3D clouds of scattered

points. With these points a mesh is generated of

triangles for the workpiece and the tool. The

modelling of the workpiece can be described in three

steps, see figure 4. At first the cross section of the

gear flank is defined by 4 points.

Cross Section of the Gear

Flank

Extrusion of Cross Section

around the central axis

Cross Section of the Gear

Flank

Extrusion of Cross Section

around the central axis

Triangulation of Surface

heel

toe

Figure 4: Modelling and triangulation of workpiece.

With the 4 points the gear width b and the toe

and the heel of the bevel gear are defined. The heel

is the face with the largest diameter respectively the

largest distance to the central axis and the toe is the

face with the smallest diameter. In order to get the

blank body of the gear the cross section is rotated

around the central axis. Finally this extruded body is

getting triangulated as described by Rütjes (2010).

Finally the tool envelope is modelled by an

extrusion of the tool profile depending on the

process kinematics, see figure 5. Like the workpiece

the tool is meshed by triangulation as well.

The data for workpiece, tool and process

kinematics can be imported in the software from a

ASCII file in the neutral data format. This data

format is a common one in gear industry and

developed by Klingelnberg (2008).

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

514

Tool Profile Extrusion of Tool

(Enveloping Body)

Triangulation of Surface

14 1

Figure 5: Modelling and triangulation of tool.

When the modelling is finished a penetration

calculation can be conducted. During the

geometrical penetration calculation the bodies of

workpiece and tool envelope penetrate each other in

compliance with the kinematics. The penetration is

realised by ray-tracing as described by Akenine-

Möller (2002). The calculated penetration volume

can be interpreted as the undeformed chip geometry

resulting from the cutting process, see figure 6. With

this undeformed geometry different characteristic

values can be calculated. It has to be mentioned that

the penetration calculation is a geometrical

calculation, i.e. that no plastic deformations are

considered.

tool

enveloping

body

workpiece

penetrated volume =

undeformed chip

geometry

Figure 6: 3D penetration calculation of triangulated

surfaces.

In order to accelerate the penetration calculation

bounding-boxes and Binary Space Partitioning

(BSP) Trees are used as depicted from Akenine-

Möller (2002). A further approach to accelerate the

simulation is the calculation of the penetration by

General-purpose computing on graphics processing

units (GPGPU) as published from Wienke (2011)

where OpenCL, CUDA, PGI Accelerator are used in

combination with graphics processing units (GPU)

in order to increase the performance.

3 CALCULATION RESULTS

3.1 Characteristic Values for Process

Analysis

The chip thickness h

and the working length l

are

characteristic values, besides the cutting forces, for

description and analysing the bevel gear cutting

process according to Klocke (2009) and Ruetjes

(2010), see figure 7. The chip thickness represents

the thickness of the undeformed chip at a certain

point on the cutting edge. The working length

represents the cutting path i.e. the contact length

between the tool and the workpiece during the

cutting. By means of these calculated characteristic

values a first analysis of the tool wear behaviour and

a process optimization is partly possible.

Current investigations from Klein (2007),

Klocke (2009) and Rütjes (2010) show that also the

characteristic values like the working rake angle γ

and relief angle α

have a significant influence on

the tool wear. Especially the flank wear of the tool is

not only influenced by the chip thickness h

and the

working length l

, but also by the geometry of the

cutting edge. The cutter geometry, in turn, is

determined by the rake and relief angle of the cutter.

These angles are defined in the German Standards

DIN 6580 (1985) and DIN 6581 (1985).

cutting direction

feed direction

working rake angle γ

working relief

angle α

working

reference plane

working

direction

rake angle γ

tool reference plane

WORKPIECE

wedge

angle β

relief

angle α

TOOL

chip thickness h

Figure 7: Calculable characteristic values.

As a conclusion it can be stated that there is

partly the possibility to analyse the tool wear by

means of the current characteristic values. But there

is no approach for a prediction of tool wear in bevel

gear cutting.

3.2 Gradient of Characteristic Values

In industrial application there are different tool

concepts. One of the concepts are the alternating half

profile blades. They are separated into outside and

MANUFACTURING SIMULATION OF BEVEL GEAR CUTTING - Simulation based Approach for Tool Wear Analysis

515

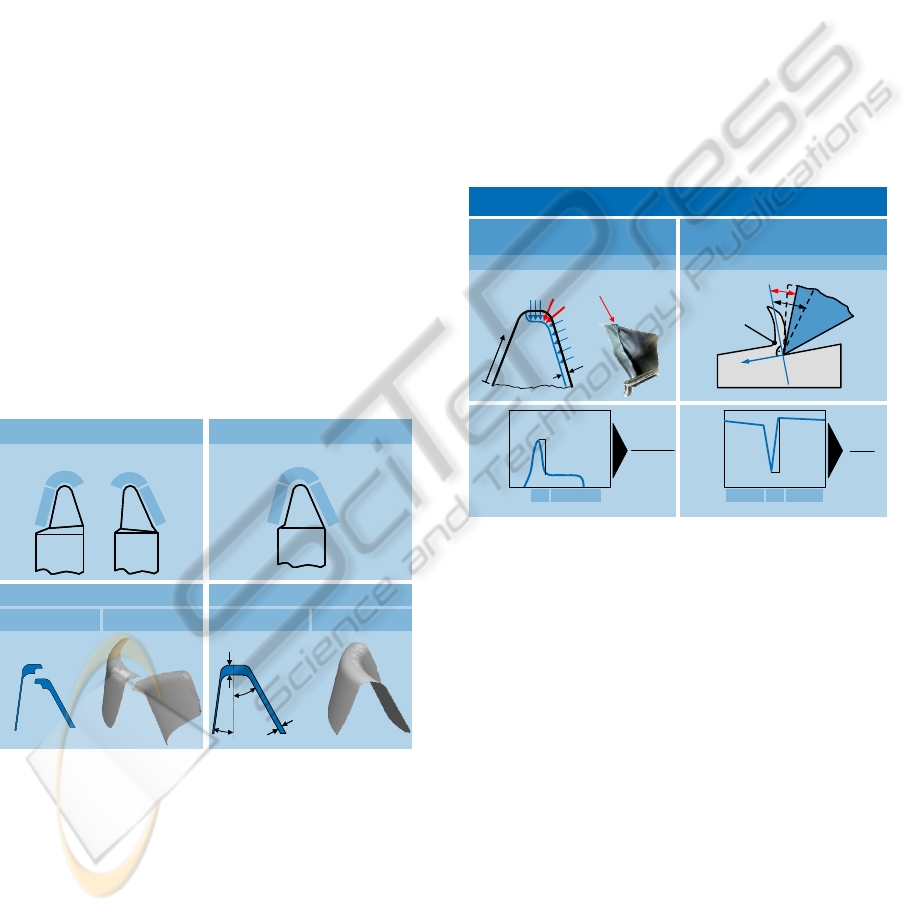
inside blades, see figure 8. Both blades are defined

as a blade group. One blade group cuts the contour

of one gap including gear root and flanks. The

outside blade cuts the concave flank and the inside

blade cuts the convex flank of the gear gap. From

this typical two-flank chips are cut. The removed

material on the flanks respectively the chip thickness

cu,flank

depends inter alia on the chip thickness on

the tip h

cu,tip

and the pressure angle δ

or δ

of the

tools:

cu,flan

= h

cu,ti

· sin(δ)

(2)

Besides the concept of alternating blades there is

the concept of full profile blades, where one blade

group consists of only one full profile blade. This

type of blades has a theoretical rake angle of γ = 0°.

The full profile blades cut both flanks (inside and

outside) at the same time. Thus, typical three-flank

chips are cut, as shown in figure 8 below right. The

advantage of this concept is the increased

productivity due to the possible increase of the

number of blade groups in the cutter head.

The chip thickness h

is the most common

characteristic value for the analysis of the cutting

process according to Rütjes (2010). A higher

pressure angle δ results in a higher chip thickness on

the flank. The chip thickness itself depends on the

feed velocity per blade group.

Half Profile Blade

Two Flank Chips

theoretical calculated

Outside Blade Inside Blade

Three Flank Chips

theoretical calculated

Full Profile Blade

OB IB

FPB

cu,flank

cu,tip

Figure 8: Cutter separation of blades.

Within the investigations of Klein (2007)

regarding tool wear in bevel gear cutting, it became

clear that especially the corner radius is critical

regarding tool wear, e.g. chipping. This is caused by

the multi-flank chip-formation at the corner radius.

Here the material of the chip is compressed and

squeezed, see figure 9. Thus, a simple analysis of the

chip thickness in this area of the tool is not

sufficient.

It becomes clear that the chip thickness h

varying along the cutting edge l

. Especially in the

transition area of the corner radius between the flank

(IB) and the tip (T) a gradient of the chip thickness

Δh

/Δl

is visible.

The spatial compression of the chip is

determined by the pressure angle of the tool as

Klocke (2010) presented. In order to consider the

compression and squeezing of the chip in the

geometrical penetration calculation the gradient of

the chip thickness can be used. The gradient

represents the varying chip thickness along the

cutting edge l

. At the tool flank the gradient is zero

due to the not varying chip thickness. This is

plausible, because of the not existing compression of

the chip material referred to the rake face

respectively the working reference plane, see DIN

6581 (1985).

Characteristic Values for Chip Compression

tool

compression of

chip

rake face

chip flow

-γ

Δh

cu,m

Δl

chip thickness

cu,m

mcu,

+γ

workpiece

chip

Δγ

workingrakeangle

Δγ

Working Reference Plane Working Cutter Plane

cu,m

Δl

cutting edge length l

cuttin edge length l

IBT OB IBTOB IBT

Gradient Chip Thickness

Δh

cu,m

/Δl

Gradient Working Rake Angle

Δγ

/Δl

Figure 9: Gradient of chip thickness and rake angle.

A higher compression of the chip results in a

higher thermal and mechanical load at the cutting

edge and the risk of tool wear.

Due to the spatial chip formation and

compression a consideration of only the working

reference plane is not sufficient. Even the working

cutter plane in which the chip flows orthogonal to

the rake face has to be considered according to

DIN 6581 (1985). Both planes take the working

direction of the cutter into account. For the

desription of the chip compression in the working

cutter plane the gradient of working rake angle

Δγ

/Δl

can be used, see figure 10. This characteristic

value represents the varying rake angle along the

cutting edge and thus the varying chip formation and

the chip compression along the cutting edge. A

rapidly changing gradient in a small area of the

cutting edge corresponds with a changing chip

formation and a varying load during the cutting. This

varying load has a negative influence on the tool

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

516

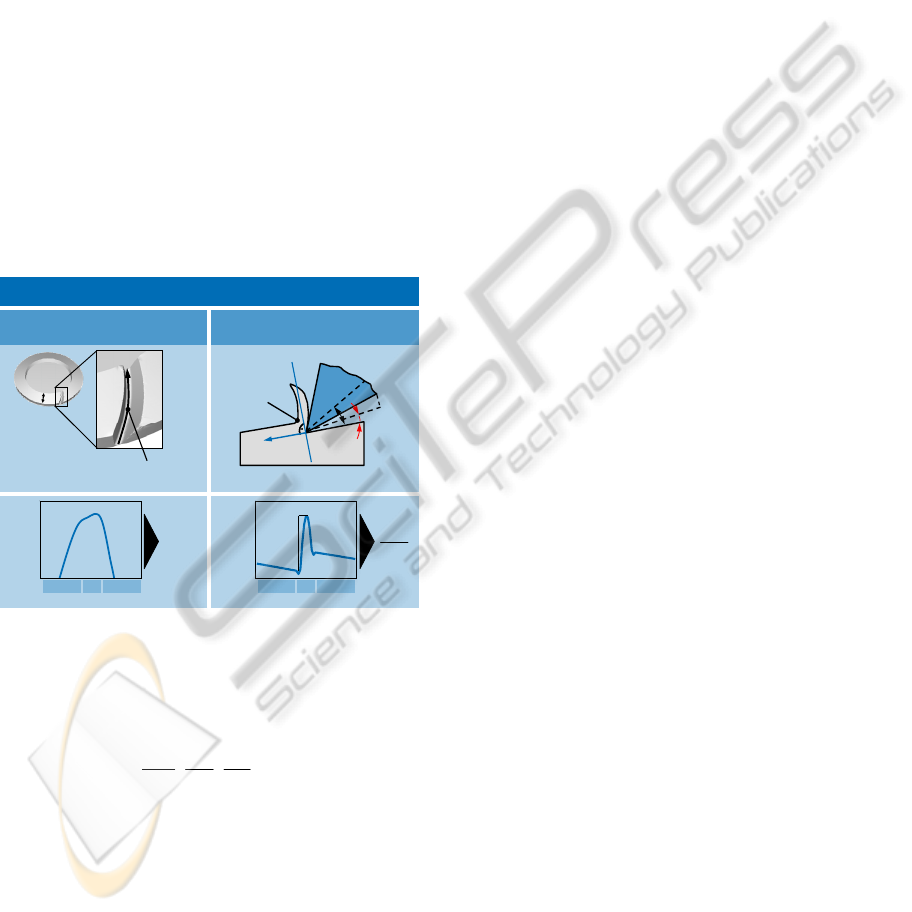
wear behaviour. Hence, the gradient should have a

minimum value.

Besides the aspect of chip compression and the

so caused tool load further characteristic values for

analysing the cutting process can be used. The entire

working length l

describes the contact length, which

the cutter is in contact with the workpiece under

consideration of the working direction, see figure 10.

So the working length is an approach for the

description of the thermal and mechanical load on

the cutting edge. A higher working length results in

a higher temperature respectively friction and thus in

higher loads on the cutting edge.

Additionally the working relief angle α

can be

used for the analysis of the tool load. The working

relief angle influences the thermal stress on the

cutting edge. Thus the gradient Δα

/Δl

is a useful

characteristic value for the alternating thermal stress

along the cutting edge. The higher the gradient the

higher the alternating thermal stresses on the relief

face of the cutter. Hence, a minimum value of the

gradient is desirable.

Characteristic Values

Working Length l

Gradient Working Relief Angle

Δα

/Δl

tool

-α

entire

workinglengthl

+α

workpiece

chip

Δα

working relief angle

Δα

Δl

OB IBTOB IBT OB OBTOB OBT

cutting edge length l

cuttin edge length l

Figure 10: Working length and gradient of relief angle.

In order to integrate the presented characteristic

values in only one value the new characteristic value

is introduced:

cu e e

sss

h Δα Δγ

lll

=⋅ ⋅ ⋅

ΔΔΔ

(3)

A high K

value results in a higher tool load and

thus in higher tool wear. With the new characteristic

value K

a first qualitative comparison of different

processes and so of the tool wear is possible. From

this an optimization of the process is feasible and a

first approach for a qualitative tool wear prediction

model is realised.

In the future the characteristic value with the tool

wear model has to be modified by weighting in order

to enable a quantitative evaluation and prediction of

the tool wear.

4 TOOL WEAR ANALYSIS

Bevel gear drives consists of a pinion and a ring

gear. The pinion is positioned at the input driving

side and the ring gear at the output side of the rear

axle drive train. In general both parts are

manufactured in a process using cutter heads which

are equipped with stick-type blades. Here the face-

milling process, as described by Klingelnberg

(2008), is used for manufacturing. The plunging

process is mostly used for the manufacturing of the

ring gear whereas the generating process is used for

pinion manufacturing.

Following different case-studies regarding tool

wear of stick type blades in industrial application

will be presented. Here the tool wear behaviour in

plunging and generating process with different tool

concepts is compared to the new characteristic value

. In this report the focus is on the discontinuous

face milling process with tungsten carbide tools in

dry cutting.

4.1 Tool Wear Analysis of Plunging

Process

In figure 11 the tool wear of two full profile blades

are presented. They are used for plunging process 1

and 2 for ring gear manufacturing. In process 1 a

cutting velocity of v

= 200 m/min and a feed ramp

of f

= 0.15 – 0.06 mm per blade group was used.

The cutter head with an outer diameter

= 231 mm. was equipped with 7 carbide tools.

The characteristic value K

was displayed in the

diagram over the unrolled cutting edge length l

which is separated into the outside blade (OB), the

tip area (T) and the inside blade (IB). The maximum

tool wear occures at the corner radius of the outside

blade (OB) to the tip area (T). In the simulation the

characteristic value K

has its maximum at the same

tool area. Additional tool wear occurs at the corner

radius of the inside blade (IB) and the tip area (T). In

this area the tool wear is less than at the other corner

radius. The same tendencies are calculated in the

simulation. Thus, the correlation of the calculated

value K

and the real tool wear is good. On the one

hand the maximum tool wear can be located by K

on the other hand the lower tool wear at the inside

blade can also be calculated.

In process 2, see figure 11 right, a cutting

velocity of v

= 150 m/min and a feed ramp of

= 0.16 – 0.10 mm per blade group was chosen.

MANUFACTURING SIMULATION OF BEVEL GEAR CUTTING - Simulation based Approach for Tool Wear Analysis

517

Ring Gear

Manufacturing (Process 2)

Ring Gear

Manufacturing (Process 1)

3 mm3 mm

100

OB IBT

7.5

3 mm3 mm

OB IBT

Full Profile BladeFull Profile Blade

rake face

[deg²/mm]

SimulationCutting Trial

Figure 11: Tool wear analysis of full profile blades.

The cutter head with an outer diameter

= 165 mm was equipped with 14 carbide tools.

Here the correlation between the tool wear from

cutting trial and the simulation is also good. The

maximum tool wear occurred at the corner radius of

the outside blade (OB) and the tip (T). Even the tool

wear in the corner radius of the inside blade (IB) can

be determined by the simulation. In this example the

tool wear is similar in both corner radii compared to

process 1, where the amount of tool wear is very

uneven. This tool wear behaviour is predictable with

the simulation by means of the characteristic value

In addition to full profile blades there is the

concept of alternating half profile blades. In order to

show the good correlation between the cutting trial

results and the simulation results the tool wear and

the characteristic value K

are presented in figure

12. Here (process 3) the focus is not only the

localization of the maximum tool wear at the cutting

edge but also the identification of the most critical

blade regarding tool wear. The maximum value for

was calculated at the corner radius of the outside

blade (OB). This correlates well with the occurred

tool wear from the cutting trials. Even the lower tool

wear of the inside blade (IB) was calculated

correctly.

Ring Gear Manufacturing (Process 3)

Inside Blade (IB)Outside Blade (OB) Inside Blade (IB)Outside Blade (OB)

IBTip

3 mm3 mm

OB Tip

3 mm3 mm

150

[deg²/mm]

SimulationCutting Trial

Figure 12: Tool wear analysis of half profile blades.

4.2 Tool Wear Analysis of Generating

Process

Generally pinions are manufactured by a generating

process. The tool and the workpiece are moving

during the cutting depending on the process

kinematics. In process 4 a feed ramp of v

= 8.72 -

12.4 °/s and a cutting velocity of v

= 230 m/min

have been used. The outer diameter of the cutter

head has been D

= 268 mm and was equipped with

32 carbide full profile blades. In this process a

generating from heel to toe is conducted. In figure

13 the occurred tool wear on the full profile blade is

shown. It is visible that the maximum tool wear is

located at the corner radius of the outside blade

(OB). Here a chipping is observed. The tool wear at

the inside blade is about 50% of the maximum wear.

125

250

IB OBTip

[deg²/mm]

Simulation

Cutting Trial

125

250

IB OBTip

[deg²/mm]

Simulation

Cutting Trial

Inside Blade (IB)

Outside Blade (OB)

Figure 13: Tool Wear Analysis for Pinion Manufacturing

with new characteristic value K

A comparison of the real tool wear in generating

process with the calculated characteristic value K

presented in figure 13, left. The calculation results

correlate well with the tool wear from the cutting

trials. Not only the location of the tool wear

correlates well with the characteristic value K

but

also the amount of tool wear.

The presented results show that now it is

possible to analyse the occurring tool wear with only

one characteristic value. Thus it is not necessary any

more to analyse the cutting process regarding tool

wear by applying and analysing many different

characteristic values, like the chip thickness or the

working tool angles, which often do not correlate

with the tool wear.

4.3 Case Study: Optimal Tool Concept

Within this report different tool concepts have been

presented. Process 1 (full profile blades) and 3 (half

profile blades) differ in the tool concept. But the

manufactured geometry of the ring gear is the same.

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

518

Not only is the ring gear the same, but also the

productivity. This means e.g. that the cutting and

feed velocity is the same and the number of blade

groups of the full profile concept is reduced to 50%.

This reduction is possible, because the number of

active cutting edges is the same for 14 half profile

blades and 7 full profile blades.

Now it is interesting to know which concept is

the best for the presented application. A comparison

of process 1 (full profile blades) and process 3 (half

profile blades) by means of the characteristic value

has been done, see figure 14.

The comparison of the calculated characteristic

value K

for the two processes shows that the

maximum tool wear appears at the outside blade

(OB) of the half profile blade concept. The value of

at the outside blade has approximately the double

magnitude of the value of the full profile blade. The

tool life of the full profile blade has been to

L = 500 workpieces whereas the tool life of the half

profile blades has been to L = 400 workpieces. Thus

there is a good correlation between the characteristic

value K

and the tool wear but there is also a good

correlation between K

and the tool life of the

different tool concepts.

Ring Gear Manufacturing (Process 1 vs. Process 3)

Full Profile Blade

OB IBT

3 mm3 mm

OB IBT

3 mm3 mm

OB IBT

3 mm3 mm

tool life outside blade

L = 400 workpiece

tool life

L = 500 workpiece

Half Profile Blade

[deg²/mm]

150

Figure 14: Comparison of different tool concepts

It can be stated that the manufacturing

simulation including the calculation of the new

characteristic value K

allows for the first time

analysing the bevel gear cutting process regarding

the expected tool wear. In the future the quantitative

prediction of tool life within a tool life model will be

realised.

5 CONCLUSIONS

Within this report the manufacturing simulation for

bevel gear cutting has been presented. At first the

modelling of the workpiece and the tool are

conducted. Under consideration of the process

kinematics the simulation can be conducted. Within

the simulation a 3D penetration calculation of

workpiece and tool are carried out. From the

penetrated volume the undeformed chip geometry

can be calculated. With information from this

penetrated volume different characteristic value like

the chip thickness can be derived. With these values

a first analysis of the cutting process regarding tool

loads and wear is possible. Unfortunately, there is

often no correlation between these values and the

expected tool wear.

Currently a new characteristic value for the tool

wear analysis is developed and implemented in the

manufacturing simulation. This new value includes

the gradient of different calculated characteristic

values over the cutting edge like the gradient for the

chip thickness Δh

/Δl

This gradient, for example,

represents the compression and squeezing of the

chip over the cutting edge. Thus, this value can be

used for the analysis of the tool load at the cutting

edge.

The comparison of the calculated new

characteristic value and the tool wear from cutting

trials show good correlations. The localization of

tool wear as well as a qualitative comparison of

different processes regarding the expected tool life is

possible. E.g. the tool life behaviour of full profile

blades and half profile blades correlates well with

the simulation results.

In the future the new characteristic value has to

be modified in order to quantify the expected tool

life. This, for instance, can be applied for increasing

the productivity of the cutting process and for

optimising the process design regarding tool

changes. Thus, the development of a tool life model

for the bevel gear cutting process has to be realised.

This tool life model has to be implemented in the

manufacturing simulation.

ACKNOWLEDGEMENTS

The authors would like to thank the German

Research Foundation (DFG) for supporting the

presented works, which are part of the research

project KL 500/89-1 “Methodik zur Vorhersage der

Werkzeugstandzeit bei Fertigungsprozessen mit

Mehrflankenspänen am Beispiel des

Kegelradfräsens”.

MANUFACTURING SIMULATION OF BEVEL GEAR CUTTING - Simulation based Approach for Tool Wear Analysis

519

REFERENCES

Akenine-Möller, T., Haines, E., 2002, Real-time

Rendering. 2

Edition, AK Peters, Massachusetts.

Brecher, C., Klocke, F., Gorgels, C., Hardjosuwito, A.,

2010. In International conference on gears.

Simulation based tool wear analysis in bevel gear

cutting. VDI, Düsseldorf, pp 1381–1384.

Chavoshi, S., 2011. In Production Engineering – Research

and Development, Tool flank wear prediction in CNC

turning of 7075 AL alloy SiC composite. Volume 5,

Number 1, pp 37-47.

N. N. 1985. Bewegungen und Geometrie des

Zerspanvorgangs. German Standard DIN 6580.

N. N. 1985. Bezugssysteme und Winkel am Schneidteil des

Werkzeuges. German Standard DIN 6581.

Klein, A.; 2007. Spiral Bevel and Hypoid Gear Tooth

Cutting with Coated Carbide Tools, Dissertation

RWTH Aachen University.

Klingelnberg, J., 2008. Kegelräder – Grundlagen und

Anwend-ungen, Springer-Verlag, Berlin Heidelberg.

Klocke, F., Brecher, C., Gorgels, C., Hardjosuwito, A.,

2009. In KT2009 – 7. Gemeinsames Kolloquium

Konstruktionstechnik. Modellierung und Simulationen

zum Kegelradfräsen – Analyse der

Werkzeugbelastung. Bayreuth pp 187-194.

Klocke, F., Gorgels, C., Herzhoff, S., Hardjosuwito, A.,

2010. In 3

WZL Gear Conference. Simulation of

Bevel Gear Cutting, Boulder, USA.

Rütjes, U., 2010. Entwicklung eines Simulationssystems

zur Analyse des Kegelradfräsens, Dissertation RWTH

Aachen University

Wienke, S., Plotnikov, D. an Mey, D., Bischof, C.,

Hardjosuwito, A., Gorgels, C., Brecher, C., In

International Supercomputing Conference, Special

Issue Paper. Simulation of bevel gear cutting with

GPGPUs—performance and productivity. Springer,

Berlin.

SIMULTECH 2011 - 1st International Conference on Simulation and Modeling Methodologies, Technologies and

Applications

520