FLOW SHOP GROUP SCHEDULING WITH LIMITED BUFFER

CAPACITY AND DIFFERENT WORKFORCE

G. Celano, A. Costa and S. Fichera

Dipartimento di Ingegneria Industriale e Meccanica, Università di Catania, Viale A. Doria 6, 95125 Catania, Italy

Keywords: Group scheduling, Workforce, Genetic algorithm.

Abstract: A permutational flowshop group scheduling problem (GSP) with sequence dependent set-up times, finite

interoperational buffer capacity and workers with different skills has been investigated in this paper. The

set-up times are influenced by the sequence of groups and the worker skill level; the manufacturing tasks on

a part are completely automated and the working times do not depend on the operator’s skill. The

minimization of the completion time is the objective of the group scheduling. A Genetic Algorithm is

proposed as an efficient tool to solve the investigated problem; a benchmark of problems has been generated

to investigate the influence of the inter-operational buffer capacity and the worker skill level on the

completion time.

1 INTRODUCTION

To be competitive in the worldwide market of

goods, companies should produce small lots of

different products at a convenient cost level and

different quality standards: consequently, their

manufacturing systems should be flexible and

reconfigurable in a short time. In this changing

environment, the workforce plays a strategic role: in

particular, at the capacity planning level a team of

operators should be correctly assembled who

provide for the sufficient skills to manufacture a

specific lot of production.

In the investigated manufacturing system, the

jobs are grouped into families in accordance to the

group technology principles and should visit an

identical sequence of machines, whose set-up times

are sequence dependent. The inter-operational

buffers between the machines have finite dimension.

In order to evaluate scheduling conditions as close

as possible to the actual process configuration, the

influence of workers is modelled, too. The operators

are not a critical resource: for this reason, the job

transfer time from one machine to its downstream

one is considered as negligible. Conversely, the

tasks related to the set-up of each group of jobs

worked on each workstation are carried out by one

operator randomly selected out from the currently

available crew of workers; thus, the set-up times

depend on the sequence of the groups visiting the

workstation and the operators skills. Finally, the

worker does not influence the processing time of

each job because each working machine is

automated. The objective of the scheduling is the

minimization of the total completion time. This is a

frequent scenario encountered in the manufacturing

of mechanical parts by means of CNC centers.

Currently, at the best of our knowledge no

optimization procedure is available from literature to

solve the investigated scheduling problem. The aim

of this paper is building the mathematical model and

designing an optimization tool able to find efficient

solutions to this problem. A proper genetic

algorithm has been designed and a benchmark of

process scenarios characterized by different numbers

of machines, families and worker skills has been

generated to study the proposed scheduling problem.

The remainder of the paper is organized as

follows: in Section 2 a review of the literature is

reported; Section 3 presents the problem statement

and the mathematical notation; then, in Section 4 the

optimization algorithm is described; the

computational results are provided and discussed in

Section 5. Conclusions and future research complete

the paper.

486

Celano G., Costa A. and Fichera S..

FLOW SHOP GROUP SCHEDULING WITH LIMITED BUFFER CAPACITY AND DIFFERENT WORKFORCE.

DOI: 10.5220/0003648704860491

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (MSIE-2011), pages 486-491

ISBN: 978-989-8425-75-1

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

2 LITERATURE REVIEW

As stated above, the investigated problem can be

approached as a Group Scheduling Problem with

sequence dependent set-up times and finite capacity

of the inter-operational buffers in presence of a multi

skilled workforce.

The flowshop Group Scheduling problem has

been challenged as an evolution of the traditional

flowshop problem, where the effect of set-up and

similarities among jobs grouped into families is

considered into the mathematical model formulation.

Several approaches to the Group Scheduling

Problem (GSP) with sequence independent set-ups

and unlimited buffer capacity have been proposed:

Wemmerlov and Vakharia (1991) extended the

implementation of constructive algorithms for the

group scheduling problem by performing an external

sequencing of families and then an internal

scheduling of parts within families. A Simulated

Annealing algorithm was proposed by Vakharia and

Chang (1990). Genetic algorithms have been

developed for the GSP by Shridar and Rajendran

(1994). Schaller (2000) has presented a comparison

of heuristics and has proposed new procedures for

the determination of effective lower bounds for the

makespan of the sequences.

Franca et al. (2005) have proposed a Genetic

Algorithm and a Memetic Algorithm to schedule

jobs within manufacturing cell modelled as a pure

flowshop problem with sequence dependent set-up

times. The scheduling problem with finite inter-

operational buffers also received attention in

literature. Nowicki (1999) proposed a tabu search

approach for the m>2 machines problem. Wang et

al., (2006) have solved the permutational flow shop

with finite inter-operational buffers by means of

hybrid GAs. A hybrid algorithm based on

differential evolution has been proposed in Qian et

al. (2009) to solve the multi-objective flow shop

scheduling with finite buffers.

The role of workforce in a plant has been

considered as an assignment problem (McDonald

2009); Diginesi et al. (2009) evaluated the effect of

the dynamic worker behaviour on the performance

of a flow line. Fowler et al. (2008) proposed a

heuristic algorithm for the workforce planning with

different operators’ skills.

3 PROBLEM STATEMENT

A notation similar to that adopted by Nowicki

(1999) for the flowshop scheduling problem with

finite interoperational buffer capacity is here

proposed and extended to the group scheduling

problem with sequence dependent set-up times,

finite buffer capacity and skilled workforce. The

jobs are clustered into g (1…..G) families, (groups),

to be worked within a line consisting of i (i=1,…..M)

working machines; for each group g, a job set

={1

,…,n

} is defined, where n

denotes the

number of jobs within the group: thus, it holds

n = n

g =1

∑

. All the machines should be visited in the

same order by the families of jobs within the mix;

thus, a permutation group flow shop can be

considered. On the machine i, the processing time of

job j

clustered within group g is denoted as

i, j

>0.

Between two machines i-1 and i there is an inter-

operational buffer having a finite capacity f

; thus,

there are M-1 finite capacity inter-operational

buffers between machines; finally, two unlimited

capacity buffers are positioned before machine 1 and

after machine M. The set-up time of the generic g-th

scheduled group on machine i is denoted as

g −1

(

)

, g

(

)

, (

(

)

, g

(

)

= SS

(

)

()

= 0

) and is sequence

dependent.

The workers (w=1…W) employed in the

manufacturing process have different skill levels,

denoted as SL

The influence of the generic worker w on the set-

up time is modeled as follows:

g −1

()

, g

()

* SL

≥1, when the worker w is assigned to machine i

to develop the set-up of group g.

Within each group g, the vector

(

)

(

)

()

,...,

(

)

()

⎛

⎝

⎜

⎞

⎠

⎟

represents a permutation

of jobs, whereas the external permutation of the

groups is denoted by

Ω=

()

,...,

()

⎛

⎝

⎜

⎞

⎠

⎟

To determine a feasible sequence of jobs, a set of

constraints related to jobs, machines and buffer

availabilities must be defined. Let us denote as

()

the starting time on machine i for the

(

)

(

)

scheduled job within g-th scheduled group.

The job routing constraint is expressed as:

()

≥ SJ

i −1,

()

+ p

i −1,

()

i = 2, ., Mj

= 1

,.,n

g = 1, . , G

(1)

FLOW SHOP GROUP SCHEDULING WITH LIMITED BUFFER CAPACITY AND DIFFERENT WORKFORCE

487

A machine is available to work a job after that

the preceding job in the sequence belonging to the

same group has been unloaded or at the completion

of the set-up activities on the machine, if the

currently scheduled job is the first within a group:

if j

()

≥ SJ

()

−1

()

+ p

()

−1

(

)

if j

(2)

()

≥ SJ

g −1

()

g −1

()

+ p

g −1

()

g −1

()

+SS

g −1

()

, g

()

* SL

(3)

valid for

GgnjMi

gggg

,...,2,1,...,2,1...,2,1 ===

With reference to the constraints related to the

generic inter-operational buffer capacity f

i+1

, the

following situations can occur.

i) the inter-operational buffer capacity f

i+1

saturated and the machine i is blocked by jobs

belonging to the same group. The job to be loaded

on machine i belongs to the same group too. Then, it

holds:

()

≥ SJ

i +1,

()

−1−f

i +1

(

)

if j

-1>f

i+1

(4a)

()

≥ SJ

i +1,

g −1

()

g −1

()

if j

-1=f

i+1

(4b)

Valid for

GgnjMi

ggg

,...,2,1,...,2...,2,1 ===

ii) the inter-operational buffer capacity f

i+1

saturated and the machine i is blocked by jobs

belonging to the same group. The job to be loaded

on machine i is the first of a new group. Then, it

holds:

()

≥ SJ

i +1,

g −1

()

g −1

−f

i +1

()

+ SS

g −1

()

, g

()

* SL

if n

-1

i+1

(5a)

()

≥ SJ

i +1,

g −2

()

g −2

()

+ SS

g −1

()

, g

()

* SL

if n

-1

i+1

(5b)

valid for

= 1,2...,mg= 2,...,G

iii) the inter-operational buffer capacity f

i+1

saturated by different groups of jobs. The job to be

loaded on machine i is not the first of a new group.

Then, it holds:

()

≥ SJ

i +1,

g −1

()

g −1

− f

i +1

− j

−1

()

(

)

if n

-1

>(f

i+1

-(j

-1

))

(6a)

()

≥ SJ

i +1,

g −r

()

g −r

+ n

g −x+1

x =2

∑

− f

i +1

− j

−1

()

⎛

⎝

⎜

⎞

⎠

⎟

if n

-1

≤(f

i+1

-(j

-1

))

(6b)

valid for

g −x +1

< f

i +1

− j

−1

()

x =2

∑

⎛

⎝

⎜

⎞

⎠

⎟

and

1, 2..., Mj

,..., n

g = 2,...,G

iv) the inter-operational buffer capacity f

i+1

saturated by different groups of jobs. The job to be

loaded on machine i is the first of a new group.

Then, it holds:

()

≥ SJ

i +1,

g−1

()

g −1

− f

i +1

− j

−1

()

+SS

g −1

()

, g

()

* SL

if n

g-1

>(f

i+1

-(j

g-1

))

(7a)

()

≥SJ

i +1,

g−r

()

g−r

+ n

g−x+1

x=2

∑

− f

i +1

− j

−1

()

⎛

⎝

⎜

⎞

⎠

⎟

+SS

g−1

(

)

, g

(

)

*SL

if n

g-1

≤(f

i+1

-(j

g-1

))

(7b)

valid for

g −x +1

< f

i +1

− j

−1

()

x =2

∑

⎛

⎝

⎜

⎞

⎠

⎟

, and

1, 2...,Mg

2,...,G

Equations (1) through (7) are valid under the

following assumptions:

()

if j

≤0,

(

)

(

)

, SJ

i,0

=0 and p

i,0

=0, f

M+1

Given a sequencing of groups and jobs within

each group, a step-by-step evaluation of the starting

inspection time

()

for each job on machine

i is obtained by computing the maximum value of

()

with respect to the constraints (1)-(7b).

Then, the completion time

()

(8)

each job on machine i can be easily computed.

The objective of the group scheduling problem is

the minimization of the makespan of the entire mix

to be worked.

max

()

= S

()

+ p

()

⎛

⎝

⎜

⎞

⎠

⎟

(9)

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

488

4 THE GENETIC ALGORITHM

The genetic algorithm developed to solve the

investigated Group Scheduling Problem requires a

proper chromosome encoding able to work with

standard genetic operators.

The chromosome encoding has been developed

to map separately the sequence of groups and the

sequences of jobs within each group: a chromosome

is coded through a two dimensional decimal array

seq(r,s), (r=1,G+1; s=1,

max max

g[]

⎧

⎨

⎩

⎫

⎬

⎭

). Rows

(1:G) contain the internal job sequence p

(g)

within

each group; the last row G+1 contains the external

group sequence: each row of the array seq(r,s) is

here considered as a sub-chromosome. The number

of columns of a chromosome array coincides with

the maximum number of jobs assigned to a single

group. The chromosome fitness is equal to the

makespan corresponding the schedule it encodes.

With this notation, a population of chromosomes can

be coded through a three dimensional array. In

Figure 1 an example of population for a problem

with G=4 and n=11 jobs, (n

=4, n

=2, n

=3, n

=2) is

presented:

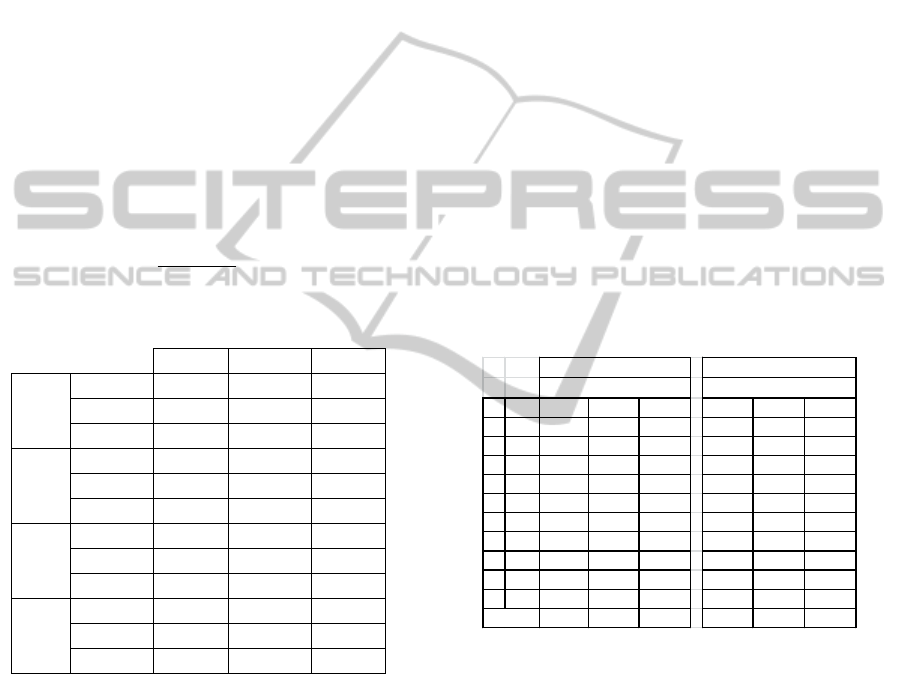
Figure 1: Population and chromosome representation.

Two different kinds of crossover operators with

an equal probability to be selected have been

implemented: the position based crossover (PBC)

and the two point crossover (TPC).

The mutation operator can work with P

probability on sub-chromosomes representing both

sequences of jobs within a group or sequences of

groups. Mutation is performed with an equal

probability of selecting one among the following

two operators: an allele swapping operator, which

performs an exchange on a random number of

alleles; and a block swapping operator, which

performs a block exchange of alleles. To prevent

from the elimination of the current best sequence,

the survival of a copy of the current fittest individual

within the population is ensured by an elitist

strategy. Conversely, the premature convergence of

the algorithm towards a sub-optimum solution due to

a rapid increase of the number of copies of «the

fittest individuals» within the current population can

occur: thus, a population diversity control technique

has been embedded in the developed GA. In the

current population, a mutation operator is applied to

those copies of chromosomes exceeding an assigned

number D

max

. To perform consecutive

intensification-diversification cycles of the

evolutionary process, after N

iterations without

improvements in the fittest individual, the mutation

probability is increased by ΔPm. When a new

minimum is found, Pm is reset to its initial value.

Once a new optimal solution is found, the algorithm

execution is continued for at least Δit further

population generations.

5 COMPUTATIONAL RESULTS

The model investigation and the GA algorithm test

have been performed by generating a benchmark of

problems accordingly to the procedure proposed in

Schaller et al. (2000) for the GSP with set-up times

and adapted to cope with finite buffer capacity and

differently skilled workers. The number n

of jobs

within a group randomly varies in the interval

[1 ,10]; the job processing times

i, j

have been

randomly generated from a uniform distribution

U [1,10]. The number of groups G and the number

of machines M range between 3 and 10: totally, ten

different line configurations have been considered.

The sequence dependent set-up times are extracted

out from three different uniform distributions to

generate three classes of problems for each line

configuration: the shorter set-up SS, (U [1,20]), the

medium set-up MS, (U[1,50]), and larger set-up LS,

(U [1,100]) classes of problems. Each class of

problems consists of 10 instances: a total number of

300 problems have been generated. Four available

buffer capacities f

=1, 2, 4, 20, for i=1,…, M-1,

between machines have been considered. Four skills

levels SL

=1.0, 1.1, 1.3, 1.5 have been assumed to

model the workforce impact on the GS problem: this

means that a worker with skill level 1.3 complete the

set-up operation in a time 30% longer than a worker

with skill 1.0. For each problem, a percentage

PW=10%, 30%, 50% of available workforce having

skill level larger then 1.0 has been considered.

Totally, 10800 scenarios have been investigated.

The following GA parameters have been selected:

number of population chromosomes N

=30;

maximum number of duplicates D

MAX

=2; equal

probability for the two crossover operators to be

selected PCR=0.5; equal probability for the two

FLOW SHOP GROUP SCHEDULING WITH LIMITED BUFFER CAPACITY AND DIFFERENT WORKFORCE

489

mutation operators to be selected PCM=0.5;

mutation probability P

=0.13; improvement in the

mutation probability ΔP

=0.05 after 500 iterations

without a new improvement in the makespan. The

maximum number of iterations is set equal to

15.000. The numerical analysis has been carried out

as follows. First of all, the benchmark of 300

problems has been optimized by assuming the

limiting condition of infinite inter-operational buffer

capacity and uniform skill level equal to SL

=1.0.

For each problem, the obtained makespan can be

interpreted as a lower bound LB that can be used to

quantify the effect of the limited buffer capacity, the

skill level and the skill variety within the working

team. Then, for each problem the optimal makespan

max

in presence of the constraints related to limited

inter-operational buffer capacity and skilled

workforce has been found. Finally, the percentage

increase of the makespan with respect to its

corresponding lower bound has been calculated:

LBC

−

=Δ

max

(10)

Table 1: Average results for each class of problems.

=1.1 SL

=1.3 SL

=1.5

=1 PW=10% 8.36% 9.41% 10.27%

PW=30% 9.30% 12.68% 16.08%

PW=50% 10.39% 16.36% 22.32%

=2 PW=10% 4.78% 5.85% 6.72%

PW=30% 5.63% 9.10% 12.33%

PW=50% 6.94% 12.49% 18.48%

=4 PW=10% 2.20% 3.02% 4.04%

PW=30% 3.09% 6.00% 9.19%

PW=50% 4.10% 9.48% 15.40%

=20 PW=10% 0.36% 1.18% 2.04%

PW=30% 1.21% 3.80% 7.01%

PW=50% 2.06% 6.68% 12.10%

Thus, a large value of ΔC

should be

interpreted as an index of significant makespan

increase with respect to the limiting condition. Table

1 shows the obtained results.

As expected, it turns out that a larger inter-

operational buffer capacity reduces the influence of

the workforce skill variability; for example, when

the inter-operational buffer capacity varies from f

to f

=4, with the same workforce allocation strategy

the averaged makespan distance from its lower

bound value decreases from 8.36% to 2.20%. In

table 1 it is also possible to appreciate the effect of

the workforce skill and the team mix: both of them

have a positive effect on the makespan.

For example, when the workforce skill level is

reduced from SL

=1.1 to 1.5, the distance from the

lower bound increases from 4.1% to 15.4% for f

and PW=50%. In the same way, the variety of team

composition PW influences the makespan: for

example, when PW varies from 10% to 50% the

distance from the lower bound increases from 1.18%

to 6.68% for f

=20 and SL

=1.3.

Finally, a second order interaction between the

worker skill level SL

and the buffer capacity f

evident: in fact, the larger is f

the lighter is the effect

of SL

on the makespan deterioration. For example,

given PW=50%, when f

=2 and SL

=1.3 it results

ΔC

=12.49%; otherwise, when f

=20 and SL

=1.3

it results ΔC

=6.68%, that is ΔC

is halved. This

happens because the available buffer capacity

partially decouples the interactions between

consecutive machines, thus reducing the probability

of starving /blocking conditions due to delays in the

set-up activities. Therefore, the worker skills need to

be carefully accounted for those manufacturing

scenarios characterized a finite inter-operational

buffer capacity.

Table 2a: variable SL

Table 2b: variable PW.

i g 1.1 1.3 1.5 10,0% 30,0% 50,0%

3 3 3,3% 5,2% 4,3% 3,3% 4,0% 4,7%

4 3 3,5% 4,4% 6,3% 3,5% 4,2% 5,6%

4 4 5,9% 7,0% 6,6% 5,9% 7,0% 8,1%

5 5 6,2% 6,7% 7,4% 6,2% 6,8% 7,9%

5 6 6,2% 7,3% 7,0% 6,2% 6,5% 7,6%

6 5 8,2% 9,0% 9,4% 8,2% 9,3% 9,7%

6 6 8,0% 8,8% 9,9% 8,0% 9,4% 10,2%

8 8 8,6% 9,9% 10,0% 8,6% 9,4% 10,2%

8 10 10,8% 11,6% 13,5% 10,8% 12,0% 13,1%

# 10 10,7% 12,0% 13,4% 10,7% 11,6% 13,3%

averag

8,4% 9,4% 10,3% 8,4% 9,3% 10,4%

fi=1 PW=10%

SLw

fi=1 Slw=1.1

Tables 2 and 3 show the same results as Table 1,

but stratified for each couple (G,M) of groups and

machines investigated in the benchmark. Table 2a

considers three levels for SL

, f

=1 and PW=10.

Similarly, Table 2b considers three levels for PW,

=1 and SL

=1.1. Table 3a shows the same ΔC%

results when f

is varied at three levels; Table 3b

considers f

, PW and SL

contemporarily varied at

three levels.

In Table 2 the worker effects quantified through

the skills level and team mix composition are

equivalent and range between 8.4% and 10.3%.

Conversely, in Table 3 the buffer effect ranges

between 2.2% and 8.4%. The interaction effect of

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

490

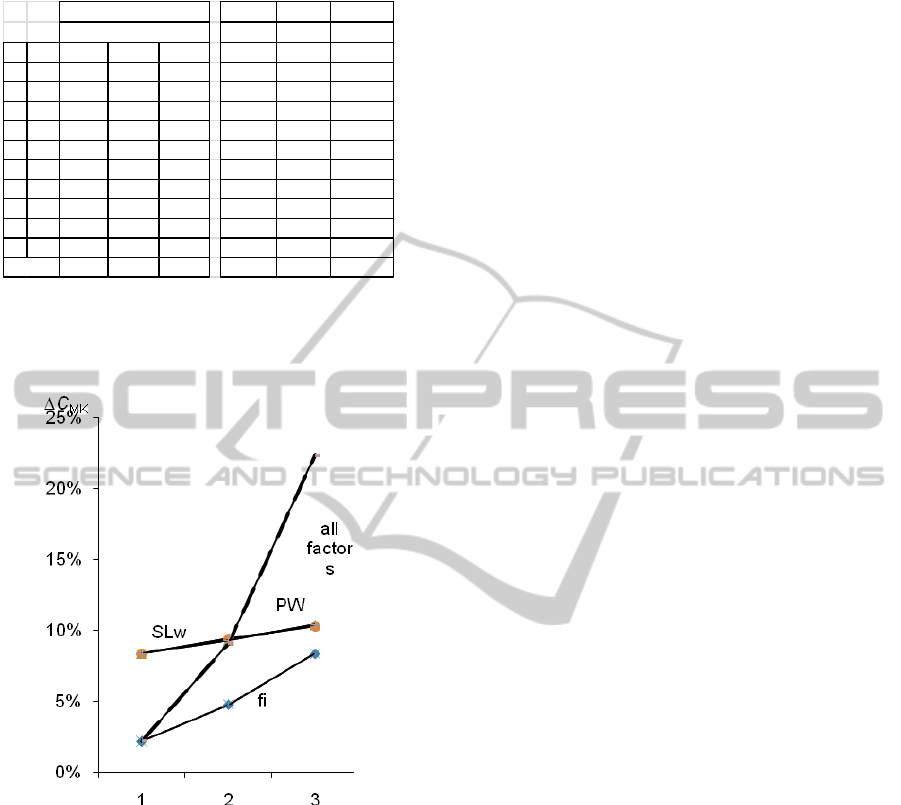
Table 3a: variable f

3b: all factors are variable.

fi=4 fi=2 fi=1

PW=10% PW=3 0% PW=50%

ig 4 2 1

Slw=1.1SLw=1.3 SLw=1.5

3 3 1,2% 2,1% 3,3% 1,2% 3,4% 13,5%

4 3 0,3% 1,5% 3,5% 0,3% 4,8% 15,7%

4 4 1,5% 3,3% 5,9% 1,5% 7,0% 18,1%

5 5 1,4% 3,6% 6,2% 1,4% 6,6% 17,0%

5 6 1,6% 2,6% 6,2% 1,6% 5,8% 17,6%

6 5 1,9% 4,8% 8,2% 1,9% 8,0% 18,8%

6 6 2,3% 4,7% 8,0% 2,3% 8,8% 20,9%

8 8 2,3% 4,5% 8,6% 2,3% 8,8% 20,7%

8 10 3,2% 6,3% 10,8% 3,2% 12,4% 28,5%

10 10 2,7% 6,6% 10,7% 2,7% 11,9% 28,2%

averag

2,2% 4,8% 8,4% 2,2% 9,1% 22,3%

PW=10% SLw=1.1

the three factors is significantly higher and ranges

between 2.2% and 22.3%. The averaged results

presented Tables 2 and 3 are graphically shown in

Figure 2.

Figure 2: Influence of factors.

6 CONCLUSIONS

A permutational flowshop group scheduling problem

(GSP) with sequence dependent set-up times, limited

interoperational buffer capacity, workers with

different skills and different mix of the working

crew has been taken into account. In the model, the

set-up times depend on both the sequence of groups

and the worker skill level; the working times have

been considered independent by the skill of the

operator because the working operations are

completely automated. A Genetic Algorithm has

been proposed as an efficient tool to solve the

investigated problem with respect to the

minimization of the total completion time. A

sensitivity analysis has been carried out on a

benchmark of problems to show the relevant

influence of all factors considered in the model. A

future development of this research will treat the

scheduling of jobs as well as the workers assignment

strategy to each machine as independent variables of

the optimization problem.

REFERENCES

Diginesi S.; Kock A., Mummolo G., Rooda J., (2009). The

effect of dynamic worker behavior on flow line

performance. International Journal of Production

Economics, 120 (2), 368-377.

Fowler J., Wirojanagud P., Gel E., (2008). Heuristics for

workforce planning with worker differences.

European Journal of Operational Research, 190 (3),

724-740.

França, P. M., Gupta, J. N. D., Mendes, A. S., Moscato,

P., Veltink, K. J., (2005). Evolutionary algorithms for

scheduling a flowshop manufacturing cell with

sequence dependent family set-ups. Computers &

Industrial Engineering, 48 (3), 491-506.

McDonald T., Ellisb K., Van Akenb E., Koellingb C.,

(2009). Development and application of a worker

assignment model to evaluate a lean manufacturing

cell. International Journal of Production Research, 47

(9), 2427–2447.

Nowicki, E., (1999). The permutation flow shop with

buffers. A tabu search approach. European Journal of

Operational Research, 116, 205-219.

Qian, B., Wang, L., Huang, D., Wang, W., Wang, X.,

(2009). An effective hybrid DE-based algorithm for

multi-objective flow shop scheduling with limited

buffers. Computers & Operations Research, 36, 209-

233.

Schaller, J. E., (2000). A comparison of heuristics for

family and job scheduling in a flow-line

manufacturing cell. International Journal of

Production Research, 38(2), 287-308.

Shridar, J., Rajendran, C., (1994). A genetic algorithm for

family and job scheduling in a flow-line

manufacturing cell. Computers and Industrial

Engineering, 27, 469-472.

Vakharia, A. J., Chang, Y. L, (1990). A simulated

annealing approach to scheduling a manufacturing

cell. Naval Research Logistics, 37, 559-577.

Wang, L., Zhang, L., Zheng, D. Z., (2006). An effective

hybrid genetic algorithm for flow shop scheduling

with limited buffers. Computers & Operations

Research, 33, 2960-2971.

Wemmerlov, U., Vakharia, A. J., (1991). Job and family

scheduling of a flow-line manufacturing cell: a

simulation study. IIE Transactions, 23(4), 383-392.

FLOW SHOP GROUP SCHEDULING WITH LIMITED BUFFER CAPACITY AND DIFFERENT WORKFORCE

491