PERSONAL ADVANCED TRAVELER ASSISTANT

Andreea Radu

, Leon Rothkrantz

1,2

and Mirko Novak

Department Man Machine Interaction, Delft University of Technology, Mekelweg 4, 2628 CD, Delft, The Netherlands

Department of SEWACO, The Netherlands Defence Academy, Den Helder, The Netherlands

Faculty of Transportation Sciences, Czech Technical University, Prague, Czech Republic

Keywords: Dynamic routing, Predicting travelling time, Personal assistant, Hand-held devices.

Abstract: In spite of numerous road management schemes and developed infrastructure the society nowadays still

faces the problem of highly congested roads due to the increasing traffic demand. The focus of this paper is

to develop a complex and integrated system that addresses the challenges of dynamic traffic assignment in

modern times. We built a design for a Personal Advanced Traveller Assistant (PTA). The main purpose of

PTA is to give routing advices depending on the users preferences and the available capacity in the network.

The system incorporates a dynamic traffic algorithm that employs a prediction model of future travelling

time. The prediction model that the algorithm uses is based on historical data. To conclude, we successfully

implemented a working prototype that uses various technologies such as Java, the Open Street Map API for

rendering the map or J2ME for the mobile phone client.

1 INTRODUCTION

In July 2007 the Federal Highway Administration

and National Cooperative Highway Research

Program in US sponsored a scanning study to

examine congestion management programs and

policies in Europe (Dantzig, 1957). This program

included four countries: Denmark, England, The

Netherlands and Germany. The focus was on the

traffic parameters and on the measures for the

deployment of congestion.

The traffic growth in The Netherlands is about 3

percent per year. In order to show some statistics,

The Netherlands reports congestion costs of 0.8

MEuro per year. The accessibility of main ports is

also affected. There is a critical need for traffic

congestion management.

From 1989 onwards, various traffic management

measures were implemented, starting from

motorway traffic management systems to overtaking

prohibitions for trucks and special police teams for

rush hours. The efforts undertaken so far to improve

the existing traffic network through traffic

management schemes by the government in The

Netherlands are the following, see Figure 1 and

Figure 2: Queue warning; Speed Harmonization;

Temporary Shoulder Lane use; Dynamic Lane

marking.

The dynamic nature of traffic can be observed in

both temporal and spatial changes in the traffc

demand, roadways capacity and traffic control

parameters. The traffic demand increases over time

until peak periods, it varies stochastic during the

peak hours and decays at the end of peaks.

A great part of the congestions are regular and

recurring at certain locations of the freeway network

and also at certain hours. These add up with the

incidents, the road maintenance fields, the weather

conditions and special events that impact traffic.

Most GPS devices that people own, when

requested a route, provide a solution based on the

minimum distance. People usually hear on the radio

if there is an incident or if there is something special

happening on the motorways. But then they have to

estimate themselves which alternative route they

should choose, how much extra time they have to

spend, whether a certain alternative is the most

convenient one and so on.

How can we best define the dynamic traffic

assignment? It can be described by the process of

dynamically selecting a path made out of roadway

segments from a trip origin to a trip destination

depending on a cost function. The cost function is

usually the travelling time.

Radu A., Rothkrantz L. and Novak M..

PERSONAL ADVANCED TRAVELER ASSISTANT.

DOI: 10.5220/0003648800740082

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2011), pages 74-82

ISBN: 978-989-8425-75-1

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Examples of traffic management measures in

The Netherlands.

Figure 2: Dynamic route information.

The complexity of traffic management is due to

the interaction of three main processes (Kemer,

2004):

 the traveller’s decision behaviour, as the decisions

of drivers influence the outcome of the traffic

network;

 the dynamic traffic assignment in a traffic

network;

 the traffic flow behaviour, in particular when

incidents and accidents occur in the network.

One approach to solve the congestion issues and

though to reduce the travel time for individuals is to

develop a route planner that incorporates current and

future traffic information when searching for the

best route. When congestions or incidents occur on

this route the planner has to compute the best

alternative solution which may lead the driver on

different roads or to a train station. The main

purpose is to minimize the travelling time by taking

into account the changes and the future situation in

the traffic network. In this area the personal

advanced travelling assistants play a crucial role.

Such an assistant has multiple functions including

that it computes the shortest travelling time-routes

based on current information received from traffic.

Within the research program Seamless

Multimodal Mobility at Delft University a Personal

Intelligent Traveller Assistant (PITA) has been

designed.

The outline of the paper is as follows. In the next

section we will describe related work on dynamic

routing. Next we will describe the used databases of

historical travel times. Next to open sources we used

to build our prototype. Then we describe the main

part the dynamic routing algorithm. We report some

experimental results and end up with a conclusion.

Figure 3: Car drivers use PITA to plan a trip.

2 RELATED WORK

Traffic assignment is defined as the problem of

finding traffic flows given an origin-destination trip

matrix and a set of costs associated to the links. One

solution for this problem is either that the driver

drives on the optimum path according to his

preferences, known as the User Equilibrium (UE)

assignment or alternatively the path that minimizes

the overall network's travelling time, known as the

System Optimum (SO) assignment.

(Wardrop, 1952) was the first one to differentiate

the two methods. A spectacular example that

actually shows that the UE assignment is in general

different from the SO solution is the Braess network.

The mathematician Dietrich Braess obtained the

paradoxical result that the addition of an arc to the

network can result in increased origin to destination

and overall travel cost. (Fisk, 1979) studied the

Braess paradox more in detail. She presented the

sensitivity of travel costs to changes in the input

flows while they are in Wardropian equilibrium.

Examples which state the fact that an increased

capacity of the input flow can decrease the travelling

time are presented.

Non-equilibrium methods assign traffic to a

single minimum path between two zones. The

minimum path infers the minimum travel time.

Minimum path algorithms include for example the

models developed by (Dantzig, 1957) and (Dijkstra,

PERSONAL ADVANCED TRAVELER ASSISTANT

1959). Other non-equilibrium methods include

diversion models, multipath assignments and

eventually combined methods.

Equilibrium methods are algorithmic approaches

which assume equal travel times. They are optimal

assignments since they are formulated on the basis

of linear or nonlinear mathematical programming

(Matsoukis, 1986). The user optimum equilibrium

can be found by solving a nonlinear programming

problem.

When a time dimension is added at the models

previously described then the DTA is obtained.

Thus, by including temporal dimensions we can

represent the real life traffic situation and compute

the traveling time. Literature surveys in this field

generally mention two main approaches for DTA:

the analytical-based models and the simulations.

The first approach which is the analytical-based

approach model considers two time indices: the time

at which the path flow leaves its origin and the time

at which it is observed on a link. In other words, the

approach assumes that the whole time is divided in

intervals. Then, static mathematical analytical

control models are applied to each interval, on the

assumption that one interval is long enough so that

drivers can complete the trip within that certain time

interval.

Literature within this area of research is

extensive. DTA has evolved a lot since the work of

Merchant and Nemhauser (Merchant and

Nemhauser, 1978) who considered a discrete time

model for dynamic traffic assignment with a single

destination. The model they assumed was nonlinear

and non-convex.

Meantime, researchers became aware that DTA

theory was still undeveloped and necessitated new

approaches to account for the challenges from the

application domain. DTA comes across a large set of

problems depending on various decision variables,

possessing varying data requirements and

capabilities of control.

The second approach is the simulation-based

model. This approach simulates the behaviour of the

drivers in different traffic settings. Due to their

capability of better representing the real world they

increased their popularity. Simulations usually try to

replicate the complex dynamics of the traffic.

Although that this is considered a different

approach, the mathematical abstraction of the

problem is a typical analytical formulation.

Next we consider some analytical-based

approaches and mathematical programming models

for DTA from literature. (Ziliaskopoulus, 2000) split

the analytical models from literature in four broad

methodological groups where the first ones are the

mathematical programming formulations. Within

this approach flow equations are deducted and a

nonlinear mathematical programming problem has

to be solved. (Merchant and Nemhauser, 1978) and

(Ho, 1980) studied such models. Due to the

complexity of a nonlinear problem, a linear version

of the model with additional constraints can be

created and solved for a global optimum using a

simplex algorithm. The linear program has a

staircase structure and can be solved by

decomposition techniques.

In optimal control theory the routes are assumed

to be known functions of time and the link flows are

considered continuous functions of time. The

constraints are similar to the ones at the

mathematical programming formulation, but defined

in continuous-time setting. This results in a

continuous control formulation and not in a discrete-

time mathematical program. (Friesz et al., 1989)

discuss two continuous link-based time formulations

of the DTA for both the SO and UE objectives

considering the single destination case. The model

assumes that the adjustments of the system from one

state to another may occur while the network

conditions are changing. The routing is done based

on the current condition of the network but it is

continuously modelled as conditions change. The

SO model is a temporal extension of the static SO

model and proves that at the optimal solution the

costs for the O-D used paths are identical to the ones

on the unused paths. They established as well a

dynamic generalization of the well known

Beckmann's equivalent optimization problem.

Simulation environments address key issues of

the traffic assignment, such as the flow's propagation

in time and the spatio-temporal interactions.

Contemporary DTA models were developed using

different traffic simulators (such as CONTRAM

(CONtinous TRaffic Assignment Model),

DYNASMART or SATURN etc.). SATURN, (Vliet

and Willumsen, 1980) is an early DTA simulation

tool that uses an equilibrium technique.

The CONTRAM, (Taylor, 1980) simulation

environment is more dynamic than the previous ones

as it allows the re-routing of cars if traffic conditions

worsen. However, it does not consider a maximum

storage capacity for roads and it assigns cars only

based on the Wardropian principle. DYNASMART

is a contemporary DTA model which uses the basic

CONTRAM concept. (Abdelfatah and Mahmasanni,

2001) show an example of a DTA model developed

by the DYNASMART approach.

(Lum at al., 1998) showed that the average speed

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

depends on the road's geometry, on the traffic flow

characteristics and on the traffic signal coordination.

A new travel time-density model was formulated by

incorporating the minimum-delay per intersection

and the frequency of intersections as parameters.

The travelling time and the traffic volume are two

main field items that have to be considered for the

speed flow study along arterial roads.

Most influencing factors that have been cited in

literature are the special incidents and holidays,

signal delays, weather conditions and the level of

congestion. The prediction error might be also

directly proportional with the length of the

forecasting period (Kisgy and Rilett, 2002).

Most of the short-term forecasting methods that

were used in literature can be divided in two

categories, namely regression methods and time

series estimation methods. A third category can be

described as combining these two. Relevant

forecasting techniques examples which belong to

previous research studies are presented in the

following paragraphs. The type of traffic data that

was used along with possible inconveniences that we

detected is included.

(Hobeika and Kim, 1994) constructed three

models for short-term traffic prediction by

combining the current traffic, the average historical

data and the upstream traffic. (Li and McDonald,

2002) use GPS equipped probe vehicles and

determine mean speed values in order to develop a

fuzzy mathematical travel time estimation model.

Time series analysis is as well a popular method to

infer the travel time prediction due to their strong

potential for on-line implementation. (Ishak et al.,

2002) describe a short-term prediction model for

speed that follows a nonlinear time series approach

and uses a single variable.

In review of literature, researchers have used

parametric models in order to forecast the travel

time, such as regression models or time series and

nonparametric models that include ANN models (Yu

et al., 2008), (Lint et al. 2005). Studies have shown

that Ann’s (including modular neural network model

and state space neural network model) is a powerful

tool to predict travel time on freeways (Lint et al.,

2005). (Yu et. al., 2008) proposed a travel time

prediction model which comprised two parts: a base

travel time and a travel time variation. The first term

is computed using a fuzzy membership value

average of the clustered historical data that reflects

the traffic pattern. The variation is predicted through

a cluster based ANN in order to capture the traffic

fluctuation.

3 DATA

Historical data may consist of single vehicles

trajectories or it may be in the form of databases of

traffic variables measurements recorded at spots on

the roadways. The broadcasters along the roadways

identify and report the travelling speed of vehicles at

fixed time intervals, the number of vehicles or the

congestion level. But most of the traffic

measurements infer the travelling speed, which is

most important for detecting the travelling time.

The raw data is processed in order to obtain

traffic indicators, such as the average speed or the

congestion level on the roads at fixed intervals.

Missing data is usually computed by interpolation

from the surrounding data (if it does not exceed a

certain interval). Other problems might come up at

the analysis stage because if the recordings are not

done for each lane there are differences between

trucks (which have a different speed limit) and cars.

An example of a travel time plot obtained from

historical data on highway A9 on the 25th of March

2003 is given in Figure 4.

Figure 4: Dynamic route information.

Traffic data can be collected by a variety of data

sensors, such as inductive loop detectors (ILD) (see

Figure 5), videos, floating cars, remote traffic

microware sensors etc. The latter represent a

relatively new technology for collecting traffic data.

But since it is still in the testing stage, only a limited

number of such sensors have been installed in the

United States. Therefore, it cannot be used for wide-

area data collection.

ANWB is one of the services which attempts to

offer a live traffic update for the highways network

in The Netherlands. The application is using data

from the monitoring system. It shows real life

graphical information about the bottlenecks on the

highway network by giving an estimate of the

PERSONAL ADVANCED TRAVELER ASSISTANT

current average speeds (see Figure 6). This traffic

information is available 24 hours a day on their

website and is free of charge. The file that we used

to fill in our database was built by collecting data

from the ANWB website. The traffic data was

collected each 10 minutes for a couple of weeks for

a roadway network that comprised the highways and

a few national roads from the country. For each road

the traveling time was extracted from the text files

that are offered by ANWB. All data was organized

in an Excel file.

For each road the following information was

stored:

 name of the road (such as A1, A2, etc.);

 names of the intersections bounding the road;

 length of the road in kilometers;

 maximum speed allowed on the road;

 associated travelling time computed based on the

maximum speed;

starting from 0:00 to 23:50 for each 10 minutes

interval the added travelling time in case of

congestion.

The missing data in some cases was computed by

interpolation from the surrounding data. After the

processing and analysis of the collected data, 4

Thursdays were chosen in order to be further used.

The file in Excel needed further processing in order

to be integrated in our application.

Figure 5: Wires in the surface of the road.

3.1 Open Source Tools

OpenStreetMap (OSM) is a collaborative project to

create a free editable map of the world. OSM

follows a similar concept as Wikipedia does, but for

maps and other geographical facts. An important

fact is that the OSM data does not resume to streets

and roads. Anybody can gather location data across

the globe from a variety of sources such as

recordings from GPS devices, from free satellite

imagery or simply from knowing an area very well,

for example because they live there. This

information then gets uploaded to OSM's central

database from where it can be further modified,

corrected and enriched by anyone who notices

missing facts or errors about the area. OSM creates

and provides free geographic data such as street

maps to anyone who wants to use them. The OSM

project was started because most maps that people

think of as free actually have legal or technical

restrictions on their use, holding back people from

using them in creative, productive, or unexpected

ways. Libraries to access the resources provided by

the project are available for multiple languages and

purposes. As an example, several rendering libraries

exist (in Javascript, Python, C and Java) and also

several editing clients that allow to interact with the

data. In order to implement the graphical user

interface of the system and to construct an initial

database out of intersections and highways from The

Netherlands, we embedded an OpenStreetMap map

viewer in the application. This was a Java panel

which allowed several listeners and functions to be

redefined.

Figure 6: Dynamic route information.

Due to the modular design of Swing component

library, the integration was an easy task.

The API of the OSM viewer provides a number

of utilities for manipulating maps, allowing us to

construct a robust user interface for our system. We

were able to:

 create the intersections for the traffic network

graph by clicking on the map.

 create directed links between two nodes - and we

assume that all the roads are straight.

 calculate distances in kilometers between nodes by

using their latitude and longitude.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

 relate geographical coordinates to plane

coordinates on the map.

 design (in different colours) paths on the map,

parallel to the main roads in order to display a

requested route.

An example of the OSM integrated in our

application is presented in Figure 7. The

intersections and the roads from the database are

displayed on the map.

4 DYNAMIC DIJKSTRA

TRAFFIC ASSIGNMENT

The starting point of the implementation for a

dynamic traffic assignment is to build the traffic

network as a time expanded graph. Given the traffic

model that we presented in the previous section we

need to implement the algorithm on a graph that is

extended in time. This is determined by the time

varying speed graphs, which we also presented in

the previous chapter. Using this representation we

can then apply known mathematical algorithms to

solve our problem. As for general routing problems,

the Dijkstra's shortest path algorithm could be

applied. The main difference to a classic traffic

assignment, in representing the network graph is that

the cost varies in time.

The input to the algorithm is represented by a

route request. A route request consists of an O-D

(origin-destination) trip demand at a specific time.

The algorithm will be applied on the network graph

and it uses the nodes, the roads and the estimation of

the travelling time based on the varying average

speed associated to each road.

The network is represented by a graph G =

{N,A}, where A is the set of directed links and N a

set of nodes. G represents the spatial network,

meaning the network of nodes and roads. In order to

represent the dynamic travel time we will use a time

extended network. The time expanded network can

be constructed in the following way: the planning

horizon is divided into variable time periods {t =

1,….T} and each node is copied for each period t so

that for each node k there are now T time-space

nodes denoted kt. For each link j in the spatial

network consider time-spaced links, jtτ joining the

entry node of link j at each time t to the exit nodes of

link j at latter times, τ = t + 1; t + 2,…. Thus for

each spatial link we have time-expanded links (jtτ), τ

= 1..T, t = 1….T. This approach brings one

constraint: the travel time has to be discretized to

intervals. If we use a very high sample rate then an

enormous graph is required whereas a lower sample

rate results in loss of information.

Figure 7: Dynamic route information.

An example of a space time extended graph

constructed in the modality that we just described is

presented in Figure 8. The space graph represented

by the nodes (A, B, C, D, E) is repeated for three

time intervals (t1 at 09:00, t2 at 09:05 and t3 at

09:10). The edges that connect the nodes from A to

E, coloured in red represent the initial connections in

the graph. For clarity these edges were kept similar

also for the other layers. But the edges in dotted

lines are the real connections of the time expanded

graph. They show the evolution in time of the speed

flow along with the travelling time in the network.

Their length, between the layers, represents the

travelling time associated to the corresponding edge

when starting at each layer. It should be noticed,

however, that not all edges were represented in the

Figure in order to keep it readable. For example, the

travelling time from B to D is 5 minutes at 09:00 and

20 minutes at 09:05.

In order to show more clearly which are the

differences between the DDTA and STA averages of

the travelling time we use Table 1. In this table the

first part shows the average time that DDTA gains

compared to STA in minutes. Some values here may

appear to be lower than expected but these are the

averages. It is worth mentioning that in the worst

case DDTA gives a result with the same travelling

time as the other algorithms, but never worse. This is

the case of the 0 values in the second part of the

table. In this part we show at each hour the route

with greatest gain in time for DDTA. We notice for

example that from Rotterdam to Amsterdam we

have a gain of 16.78 minutes at 8 o'clock.

PERSONAL ADVANCED TRAVELER ASSISTANT

Figure 8: Dynamic route information.

5 MODEL

PTA gives the traveller routing advices during his

trip starting from departure to destination. The

traveller will benefit of the best available solution

according to his preferences at the departure time. If

unexpected events occur, it will result in

modifications during the trip. PTA should distribute

the traffic in the network so that it satisfies the

preferences of the users by taking into account the

availability in the network. The system will use

continuously updated traffic flow information. This

information would be available from the GPS-

equipped mobile phones of the users. Given that the

system knows which are the route requests and the

routes assigned already to drivers it can give a

prediction of the travelling times on the roads in the

future. This can be done by training a neural

network on the relation between various traffic

parameters such as the traffic stream and the

travelling time.

If we return to the individual routes assignment,

in case of an incident/road work the system informs

the traveller on the delays and best alternative

solutions. The driver will be also informed on the

travelling time associated to the recommended

alternative, the types of roads and eventually the

advantages/disadvantages. As we already

mentioned, PTA connects to the users by a hand

held device. This can be a smart phone, a routing

device or a PDA.

PTA is a distributed system that links the users to

the central server. All components are connected

through Internet. Users are connected to the server

but they can also communicate among themselves

by using ad hoc wireless networks. A possibility to

do this is by using the wireless network between

light poles on the highways. In Table 1 we list the

advantages and disadvantages of a distributed

system.

Table 1: Dynamic Dijkstra Algorithm compared to Static

Dijkstra Algorithm.

The advantage of PTA is that if the system

becomes a centralized one (because of network

problems) it still manages by connecting to the other

cars in order to get the information it needs. Figure 9

depicts the architecture of PTA. The main server has

to be connected to the roads and nodes database, to

the historical database and to an incidents database.

As we already mentioned, it is important for PTA to

benefit of live traffic information. The system is

designed in such a way that it uses the information

from the vehicles that already exist in the network.

The GPS-equipped mobile phones report their

positions at fixed time intervals. Moreover, the

routes of the vehicles are supervised, meaning that

the system knows the origin, the destination and the

departure time of each route. In this way the

travelling time of the traffic flow in the future can be

estimated.

6 CONCLUSIONS

As we mentioned in the introduction of this thesis,

our main purpose was to build a dynamic traffic

assignment. An important component of this is the

prediction of the travelling time. In this paper we

proposed a prediction method that would update the

historical data based on supervising the routes in the

network together with the real time traffic

information.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

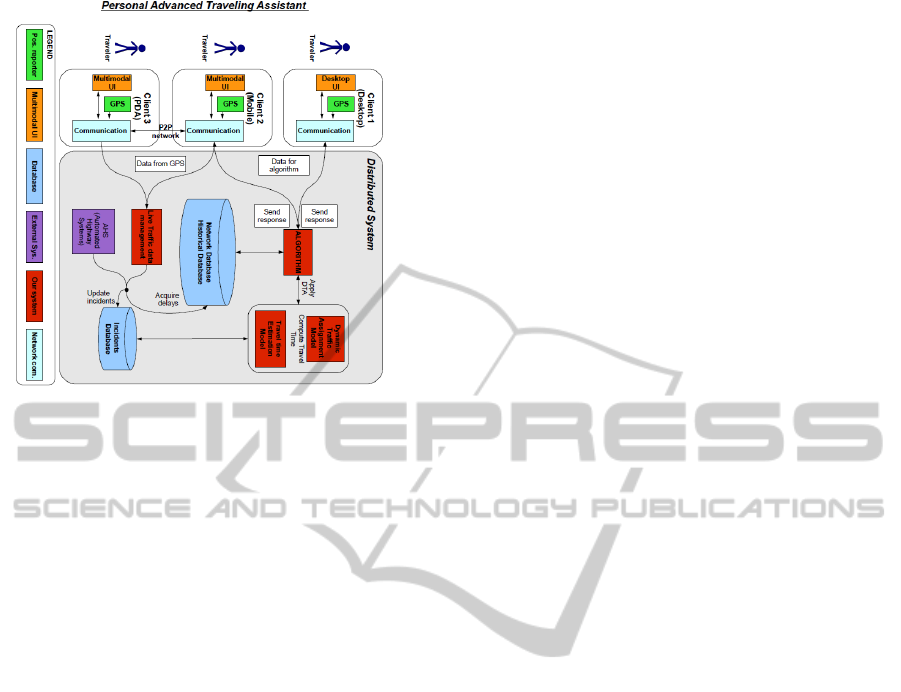
Figure 9: Dynamic route information.

Our prototype implements an algorithm that is a

time dimensional extended version of Dijkstra

shortest path algorithm. The main difference is that

our algorithm takes into account the traffic

variations in time. The cost function in the algorithm

is associated with the travelling time. The algorithm

uses the prediction model that we described

previously. Because of the fact that the algorithm

gives the route with the shortest time to each user we

may categorize it as a user equilibrium assignment.

However, we assume that just a part of the drivers in

the network are connected to the system. If we deal

with the whole network the situation would change.

The results of the algorithm were compared to

the results of two variants of the static Dijkstra

algorithm, one that computes the shortest path and

one that uses the fastest roads given their maximum

speed limit.

We developed a complex design for an advanced

traveller information system that relies on the

concept of distributed systems. The system that we

designed integrates the use of live traffic information

that derives from tracking the individuals and use of

highway sensors. Travellers are routed through hand

held devices which can be their mobile phones.

Another important feature of the system that we

designed is that it is usable by everybody, without

any special training or knowledge needed. In order

to get more insight into users’ preferences with

regard to such a system we did a user survey that

mostly confirmed our expectations but also brought

new ideas.

The system is also seen as a intelligent assistant

as it has the capability to detect, learn the user's

profile and associate it with his schedule. It

combines this information with the traffic data and

advises him about the best route to take.

Building the design of such a system was a

challenging experience as there are numerous

aspects to be taken into account. For each feature

that we included in the design we also presented a

possible manner to achieve it.

Given the huge complexity of the system we

chose to implement the most important components

with their basic characteristics.

REFERENCES

Kerner, B. S.: The Physics of Traffic. Springer (2004).

Wardrop, J.: Some theoretical aspects of road traffic

research. Proceedings of the Institution of Civil

Engineers, Part II, Vol. 1. no. 36, (1952) 352-362.

Fisk, C.: More paradoxes in the equilibrium assignment

problem, Transportation Research Part B:

Methodological, Vol. 13, no. 4, (1979) 305-309.

Dantzig, G. B.: Discrete-variable extremum problems,

Operations Res. Vol. 5. (1957) 266-277.

Dijkstra, E. W.: A note on two problems in connexion

with graphs, Numer. Math., Vol. 1. (1959) 269-271.

Matsoukis, E. C.: Road traffic assignment, a review, part

1: non-equilibrium methods, Transportation Planning

and Technology, Vol. 11. no. 1. (1986) 69-79.

Merchant, D. K., Nemhauser, G. L.: A model and an

algorithm for the dynamic traffic assignment

problems, Transportation Science, Vol. 12. no. 3.

(1978) 183-199.

Ziliaskopoulos, A. K.: A linear programming model for

the single destination system optimum dynamic traffic

assignment problem, Transportation Science, Vol. 34.

no. 1 (2000) 37-49.

Ho, J. K.: A successive linear optimization approach to the

dynamic traffic assignment problem, Transportation

Science, vol. 14, no. 4. (1980) 295-305.

Friesz, T. L., Luque, J., Tobin, R. L., Wie, B. W.:

Dynamic network traffic assignment considered as a

continuous time optimal control problem, Operations

Research, Vol. 37. no. 6. (1989) 893-901.

Vliet, Hall, M. V., Willumsen, D.: Saturn - a simulation

assignment model for the evaluation of traffic

management schemes., Traffic Engineering and

Control, Vol. 21. no. 4. (1980) 168-176.

Taylor, N.B.: Contram dynamic traffic assignment model,

Networks and Spatial Economics, (1980) 297-322.

Abdelfatah, A, Mahmassani, H.: A simulation-based

signal optimization algorithm within a dynamic traffic

assignment framework, in Intelligent Transportation

Systems, Proceedings. 2001 IEEE, (2001) 428-433.

Lum, K. M., Fan, H. S. L., Lam, S. H., Olszewski, P.:

Speed-flow modeling of arterial roads in Singapore,

Journal of Transportation Engineering, Vol. 124, no.

3, (1998), 213-222.

PERSONAL ADVANCED TRAVELER ASSISTANT

Kisgy, L., Rilett, L. R.:Travel time prediction by advanced

neural network, Periodica Polytechnica Ser. Civ. Eng,

Vol. 46 (2002).

Hobeika, A., Kim, C. K.: Traffic flow-prediction systems

based on upstream traffic, (1994) 345-350.

Li, Y., McDonald, M.: Link travel time estimation using

single GPS-equipped probe vehicle, (2002) 932-937.

Ishak, S., Al-Deek, H.: Performance evaluation of short-

term time-series traffic prediction model, Journal of

Transportation Engineering, Vol. 128, no. 6, (2002)

490-498.

Yu, J., Chang, G.-L., Ho, H., Liu, Y.: Variation based

online travel time prediction using clustered neural

networks, (2008).

Lint, J.,van, Hoogendoorn, S., van Zuylen, H.: Accurate

freeway travel time prediction with state-space neural

networks under missing data, Transportation Research

Part C: Emerging Technologies, vol. 13, no. 5-6,

(2005) 347-369.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics