SCENE TRANSITION NETS SIMULATOR FOR MULTI-ASPECT

MODELING OF DISCRETE-CONTINUOUS HYBRID SYSTEMS

Takeshi Tateyama

, Seiichi Kawata

, Yoshiki Shimomura

, Kentaro Watanabe

and Ryosuke Chiba

Graduate School of System Design, Tokyo Metropolitan University, Asahigaoka 6-6, Hino-shi, Tokyo, Japan

Advanced Institute of Industrial Technology, Higashi-Ohi 1-10-40, Shinagawa-ku, Tokyo, Japan

Keywords:

Discrete-continuous hybrid systems, Simulation, scene transition nets (STNs), Manufacturing systems,

Multi-aspect modeling.

Abstract:

Scene Transition Nets (STN) are graphical modeling tools and simulators for discrete-continuous hybrid sys-

tems. Designers have previously built complex STN models of large-scale systems on the basis of a single

aspect. However, many large-scale systems consist of several sub-systems designed for different purposes and

based on different aspects. In addition, these subsystems are complexly intertwined with each one another.

For verifying the behavior of such complex systems in simulations, it is necessary to construct multiple STN

models of the subsystems, integrate them by taking into account the relationships among the subsystems, and

simulate them in parallel. Kawata has proposed ”multi-aspect modelingh using STNs in order to realize above-

mentioned modeling concepts. However, the interaction of the sub-STN models with other models is difﬁcult

according to the basic STN concepts. This shortcoming interferes with the practical implementation of multi-

aspect modeling. The authors overcome this shortcoming by enabling the sharing of the state variables of the

actors (actors correspond to tokens in Petri nets). Called ”actor-link”, the simple concept enables to construct

complex layered and parallel structures of STNs and perform multi-aspect modeling. The experimental results

for the modeling and simulation of certain complex industrial systems demonstrate the effectiveness of the

proposed method and simulation tool.

1 INTRODUCTION

Simulation is an effective technique for verifying the

behavior of complex systems such as manufacturing

systems and chemical plant systems. However, many

complex industrial systems are actually combinations

of both continuous systems and discrete-event sys-

tems and are called ghybrid systems.h Hence, it is

difﬁcult to model and simulate such systems by us-

ing only the modeling methods applicable to contin-

uous systems (e.g., differential equations) or those

used discrete-event systems (e.g., Petri nets(Murata,

1989)). Kawata et al. have proposed scene transi-

tion nets (STNs)(Kawata et al., 1994a)(Kawata et al.,

1994b) as graphical modeling and simulation tools for

discrete-continuous hybrid systems. Although STNs

are based on the concept of Petri nets, in STNs, de-

signers construct models of continuous systems us-

ing differential equations and then embed them into

discrete-event system models. By using STNs, de-

signers can easily construct models of hybrid sys-

tems and conduct simulations. STN programming re-

quires STN designers to possess considerable object-

oriented programming skills and excellent knowl-

edge. In our study, we aim to develop an gSTN graph-

ical user interface (GUI) simulator(Tateyama et al.,

)(Tateyama et al., 2010)h that will enable designers to

easily and graphically edit and simulate STN models.

System designers have previously built complex

STN models of large-scale systems on the basis of

a single aspect. However, many large-scale systems

consist of several subsystems designed for different

purposes and based on different aspects. In addition,

these subsystems are complexly intertwined with one

another. For verifying the behavior of such complex

systems in simulations, it is necessary to construct

multiple models of the subsystems, integrate them

by taking into account the relationships among the

subsystems, and simulate them in parallel. Kawata

et al. have proposed ”multi-aspect modelingh using

STNs(Kawada et al., 1996) in order to realize the

abovementioned modeling concepts. In this model-

ing method, it is necessary to create models of inter-

actions among submodels. However, an actor can be

467

Tateyama T., Kawata S., Shimomura Y., Watanabe K. and Chiba R..

SCENE TRANSITION NETS SIMULATOR FOR MULTI-ASPECT MODELING OF DISCRETE-CONTINUOUS HYBRID SYSTEMS.

DOI: 10.5220/0003650104670475

In Proceedings of the 8th International Conference on Informatics in Control, Automation and Robotics (MSIE-2011), pages 467-475

ISBN: 978-989-8425-75-1

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: STN components.

present only in one scene at a time and cannot com-

municate with other actors according to the basic STN

concept. These shortcomings make the interaction of

the sub-STN models with other models difﬁcult. As

a result, this problem interferes with the practical im-

plementation of multi-aspect modeling.

In this study, the authors overcome this shortcom-

ing by enabling the sharing of the state variables of

the actors. This concept is called ”actor-link”. In ad-

dition, the authors implement the concept in the STN

GUI simulator as useful functions so that the design-

ers can easily apply the modeling methods to a wide

variety of systems. The proposed method and tool

enable system designers to construct STN models of

complex systems as a combination of simple submod-

els based on different aspects and make large-scale

modeling and veriﬁcations by multiple professionals

easy. Our tool also assists professionals in verifying

the behavior of complex systems from many different

aspects and meet the users’ requirements using graph-

ical STN simulations.

The experimental results for the modeling and

simulation of certain complex industrial systems

demonstrate the effectiveness of the proposed method

and tool.

2 SCENE TRANSITION NETS

(STN)

An STN is a graphic modeling method for discrete-

continuous hybrid systems: it uses the concept of gac-

torsh and gscenes.hIt is based on the Petri net, which

is a modeling method for discrete event systems. It

can express hybrid systems by using the concept of

a Petri net and by inputting differential equations in

scenes. In an STN, an actor corresponds to a sub-

system of a hybrid system. Designers can simulate

interactions between the subsystems that act in paral-

lel by describing the models by using object-oriented

programming languages (e.g. Smalltalk, JAVA). An

STN comprises actors, scenes, transitions, and arcs,

as shown in Figure 1. Details of these components

are described below.

2.1 Actor Classes and Actors

Actors in an STN correspond to the tokens in a Petri

net. However, unlike tokens, actors have state vari-

ables whose values change dynamically. An actor is

one of the objects in an STN and belongs to an ”actor

class”. Actors belonging to the same actor class have

common data structures (same types of constants and

variables) and are called instances of the actor class.

Actors are deﬁned as subsystems of an entire system,

which is deﬁned as an observed system. It is a set of

actors that interact with each other. Through these

interactions, the states of actors and state variables

change according to their dynamics described by us-

ing differential equations in scenes, as explained in

the following section.

2.2 Scenes, Castings, and Performers

Scenes in an STN correspond to places in a Petri

net. In an STN, scenes are combinations of activi-

ties deﬁned in discrete event systems and dynamics

for changing variables of actors in the activities. Fig-

ure 1 shows STN components, including a scene and

an actor, by using the description format of an STN.

The circle A1 shown at the bottom of the scene indi-

cates the location of the actor named A1. The circle

A at the middle of the scene indicates casting of the

scene. A casting of a scene indicates an actor class

whose instances (actors belonging to the actor class)

can transit to the scene. An actor located in a scene is

called a performer of the scene. Designers write dy-

namics by using differential equations in each scene

in order to dynamically change variables of the per-

formers of the scene.

2.3 Transitions and Arcs

Transitions in an STN correspond to those in a Petri

net and indicate scene transition boundaries that cor-

respond to events in discrete event systems. Transi-

tions and scenes are connected by arcs. Transitions

connected to scenes with input arcs leading into the

scenes are called input transitions of the scenes. In

contrast, transitions connected to scenes with output

arcs exiting from the scenes are called output transi-

tions of the scenes. In a similar manner, transitions

have some input scenes and output scenes. Design-

ers write ﬁring conditions of the transitions for which

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

468

Figure 2: STN GUI simulator.

the actors in input scenes transit to output scenes, and

they write transit rules for the state variables.

2.4 Related Methods

This section describes related modeling and simu-

lation methods for discrete event systems and hy-

brid systems. Petri nets(Murata, 1989) are popular

methods to model and simulate discrete event sys-

tems. However, it is difﬁcult to model and to sim-

ulate changes in continuous values. Fishwic have

proposed a modeling approach for hybrid systems by

combining different types of multiple modeling meth-

ods(Fishwick, 1991). However, it is difﬁcult for this

approach to model and simulate behaviors of multiple

sub-systems, which operate concurrently, inﬂuencing

each other. Arena(W. D. Kelton and Sturrock, 2003)

is also a very useful software tool for discrete event

systems. This tool can be used as a simulation tool

for discrete-continuous hybrid systems, However, it is

not easy for designers to build hybrid models because

this tool is not designed on the premise of hybrid sys-

tem simulation.

3 STN GRAPHICAL USER

INTERFACE (GUI) SIMULATOR

The present authors have developed an STN GUI

(Graphical User Interface) simulator so that design-

ers can easily edit and simulate STN models. Fig-

ure 2 shows an overview of the GUI simulator. This

simulator consists of an STN edit toolbar, workspace,

simulation toolbar, and graph windows. In simulation

phases, it displays multiple graphs which show dy-

namical changes in designated actors’ state variables.

The designers analyze the behaviors of continuous

variable systems by observing these graphs. In addi-

tion, it also displays animation that shows the transi-

tions of the actors and they also analyze the behaviors

of the actors as discrete event systems. The details of

these components are described in (Tateyama et al., ).

4 MULTI-ASPECT MODELING

USING STN

Many large-scale industrial systems such as manufac-

turing systems include multiple subsystems that are

constructed for different purposes and different as-

pects. In addition, they include layered and parallel

structures that operate concurrently, inﬂuencing each

other. For verifying the behavior of such complex

systems in simulations, it is necessary to construct

multiple models of the sub-systems, integrate them by

taking into account the relationships among the sub-

systems and simulate them in parallel. For example,

the model of an automated transportation system in

a factory can be divided into the following three dif-

ferent submodels: (1) a dynamics model of an auto-

mated guided vehicle (AGV), (2) a decision-making

model of the AGV (for planning the navigation of

the AGV in a factory-like environment), and (3) a

model of transportation sequences of the product and

its parts. To verify the behavior of this system us-

ing STNs, it is important to construct three sub-STN

models through a thinking process called ”envision-

ing(de. Kleer, 1977)” and conduct simulations in par-

allel. Kawata et al. call this concept gmulti-aspect

modelingh using STNs(Kawada et al., 1996). In this

SCENE TRANSITION NETS SIMULATOR FOR MULTI-ASPECT MODELING OF DISCRETE-CONTINUOUS

HYBRID SYSTEMS

469

Figure 3: Possibility of communication between actors.

modeling method, as multiple independent STN mod-

els are constructed, the same actor is necessarily in-

cluded in multiple submodels(Kawada et al., 1996).

In the abovementioned example, the same AGV is in-

cluded in the three submodels (1), (2), and (3). The

behavior of an actor in a submodel inﬂuences behav-

ior of the actors in other submodels. Therefore, it is

necessary to create models of interactions among sub-

models for effective multi-aspect modeling. However,

an actor can be present only in one scene at a time and

cannot communicate with other actors (as shown in

Fig.3) in the basic STN concept. These shortcomings

make the interaction of sub-STN models with other

models difﬁcult.

In this section, the authors resolve this shortcom-

ing by enabling the sharing of the state variables of

actors. This concept is called ”actor-link”. The fol-

lowing subsections describe this concept in detail and

show that this simple concept enables us to construct

layered and parallel structures of STNs and to per-

form multi-aspect modeling.

4.1 Actor-link

Figure 4 shows the concept of actor-links for shar-

ing the state variables of actors. In this concept, ac-

tors that are instances of the same actor class share

their state variables. Figure 4 shows that actors

,...,A

, which are instances of actor A, share

their state variables x,y,z,.... Each shared state vari-

able is incremented according to multiple differential

equations (continuous system models) written in mul-

tiple scenes at every simulation time step. Therefore,

the variation in x is expressed by the following for-

mula.

∆x(t) =

∑

i=1

∆x

(t) (1)

Here, ∆x(t) is the variation in the state variable x at

time t. ∆x

(t) is the variation in x in the submodel i.

This concept realizes parallel simulation of mul-

tiple sub-STN models by considering the interactions

among them. The authors have implemented this con-

cept in the STN GUI simulator. Figure 12 shows a set-

sub-STN

model 1

shared state variables

actor class A

actors (instances of actor class A)

x, y, z, …

link share update

STN model

sub-STN

model 2

sub-STN

model N

Figure 4: Concept of actor-links.

ting window of the actor-links. This ﬁgure indicates

that actors ”AGV1,” ”AGV2,” ”AGV3,” and ”AGV4”

share their state variables. With this interface, users

can easily use the function of actor-links.

4.2 STN Modeling of Layered

Structures and Parallel Structures

using Actor-link Concepts

The actor-link concept enables us to construct lay-

ered and parallel structures of STNs and realize multi-

aspect modeling. Details of the manner in which lay-

ered and parallel structures are constructed are given

below.

4.2.1 Layered Structure Modeling

Figure 5 shows a two-layered structure of an STN

model. Submodel 1 is an upper model, and submodel

2 is a lower model. This ﬁgure shows that submodel

2 is a detailed model of scene S1-2 in sub model 1. In

this model, actor A1 in submodel 1 and actor A2 in

submodel 2 are made equal by using actor-link con-

cepts. For example, in the modeling of manufacturing

systems, an upper model is a rough process sequence

and a lower model includes detailed processes in the

sequence. This multi-aspect modeling is based on two

aspects (a rough process sequence and a detailed pro-

cess).

4.2.2 Parallel Structure Modeling

Figure 6 shows a parallel structure in which three sub-

models run in parallel and interact with each other. In

this model, actors A1, A2, and A3 in submodels 1, 2,

and 3, respectively are considered to be equal. All the

state variables of the three actors are updated accord-

ing to the differential equations written in all the three

submodels. For example, a parallel process system

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

470

S2-2

submodel 2

actor-link ( A1 = A2 )

S1-2

submodel 1

S1-1

S1-3

detailed model of S1-2

S2-3

S2-1

upper

model

lower

model

Figure 5: Layered structure modeling using actor-link con-

cepts.

S1-x

submodel 1

Actor-link

( A1 = A2 = A3 )

S2-y

submodel 2

S3-z

submodel 3

Figure 6: Parallel structure modeling using actor-link con-

cepts.

S1-x

S2-z

S3-y

communication

submodel 1 submodel 2

submodel 3

( communication model )

actor-link

( A1 = A2 )

actor-link

( B1 = B2 )

Figure 7: Modeling of communication between two differ-

ent actors.

which processes in parallel parts by using three types

of process machines.

4.2.3 Modeling of Communication among

Different Actors

Different actors in different submodels can commu-

nicate by using actor-link concepts. In Fig.7, actors

A1 and B1 communicate through the communication

model (submodel 3) because actors A1 and A2, and

B1 and B2 are considered equal. For example, it

is possible to simulate autonomous distributed con-

trols of AGVs that wirelessly communicate with each

other.

It may possible to construct STN models of highly

complex systems by combining the abovementioned

structures.

5 AN EXAMPLE: AN

AUTOMATED

TRANSPORTATION SYSTEM

USING A BATTERY-POWERED

AGV

5.1 An Automated Transportation

System using a Battery-powered

AGV

This section describes an example of the modeling

and simulation of an automated transportation system

with a battery-powered AGV (automated guided vehi-

cle). Figure 8 shows the outline of the example. The

purpose of this system is to produce the products that

consist of parts A, processed by a process machin-

ery, and parts B. The AGV carries parts A from buffer

1 to the process machinery using a battery-powered

AGV. The AGV moves between buffer 1 and the pro-

cess machinery (distance: 50[m]) and between buffer

1 and the battery changer(distance: 10[m]). The AGV

can carry only one set of parts A at a time. After the

AGV throws parts A in the process machinery, it re-

turns to buffer 1. When the AGV reaches buffer 1,

it checks its battery voltage. If the voltage is higher

than V

, it continues to carry other parts; otherwise,

it goes to the battery changer in order to replace its

battery. The authors deﬁne the dynamics of the AGV

and the voltage of the batteries as follows:





˙x









0 ±R 0

0 −ψ

J ψ/R

0 aψ/R

−a/R

















−T l/J − R





(2)

Here, x(−10 ≤ x ≤ 50)[m] is the current position of

the AGV, ω [rad/sec] is the angular velocity of the

AGVfs motor, V

[V] is the current voltage of the

battery, R is the ﬁnal reduction ratio, R

[Ω] is the

armature circuit resistance, J[kgm] is the total mo-

ment of inertia of the rotational system, ψ[Nm/A] is

the torque constant of the armature, Tl[Nm] is the

counter torque supplied to the motor shaft, R

[Ns/m]

is the viscous frictional drag, and a[V/As] is the char-

acteristic constant of the battery. The initial value of

is 100[V] and V

is 40[V]. The purpose of this sim-

ulation is to observe the AGVfs behavior, changes in

the battery voltage and efﬁciency of transportation of

the parts.

SCENE TRANSITION NETS SIMULATOR FOR MULTI-ASPECT MODELING OF DISCRETE-CONTINUOUS

HYBRID SYSTEMS

471

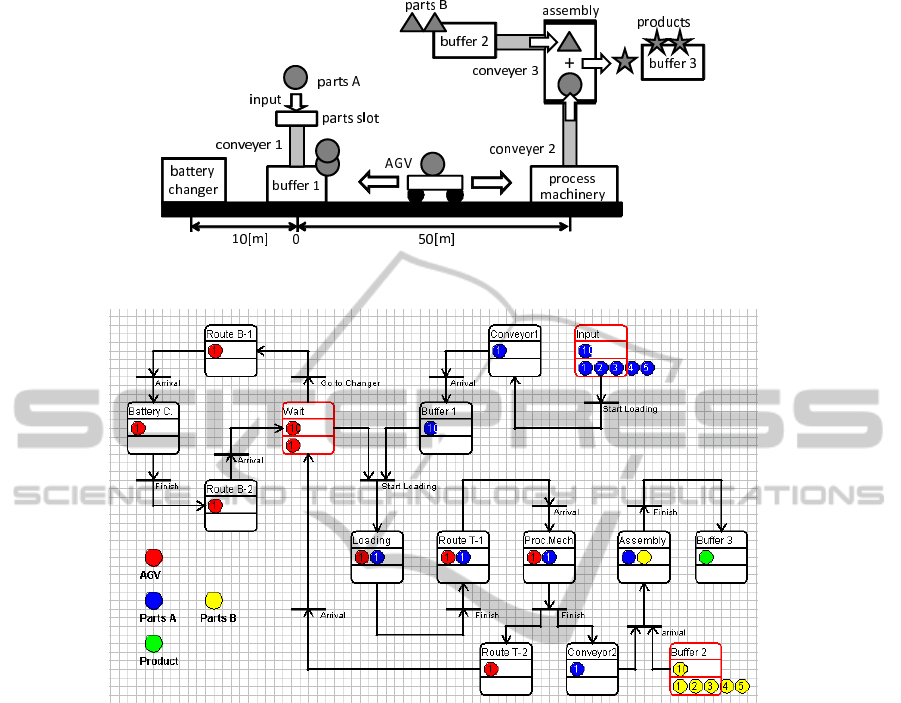
Figure 8: An automated transportation system using a battery-powered AGV.

Figure 9: An STN model constructed from a single aspect.

5.2 STN Modeling from a Single Aspect

Figure 9 shows an STN model constructed from a sin-

gle aspect using our old version simulator. This model

illustrates the whole transportation system by using a

single network. However, this modeling method has

some shortcomings. It includes several models con-

structed from different aspects such as models of the

AGV dynamics, temporal changes in the battery volt-

age, procedure of change of battery, and transporta-

tion routes. When we construct a complex system

model using a single STN, the procedure of modeling

also becomes complex. For example, we have to write

the AGV dynamics and battery voltage model for all

the scenes where the AGV functions. Speciﬁcally, we

have to write equations (2) for four scenes (routes T-1,

T-2, B-1, and B-2). It also requires time and effort to

rewrite them when we change the speciﬁcations of the

system. This example is relatively simple. However,

when system designers want to simulate a large-scale

and complex system model, it is difﬁcult for them to

express it by using a single network and to observe its

behavior.

5.3 Multi-aspect STN Modeling and

Simulation

In this section, we have tried to construct the follow-

ing four simple sub-STN models and integrate them

for a concurrent and hierarchic simulation: (1) an

AGV dynamics model, (2) an AGV state model, (3) a

transportation process model and (4) a battery change

process model. The following subsections describe

the details of these submodels.

5.3.1 An AGV Dynamics Model

An AGV dynamics model is a very simple model,

which consists of only two scenes and an actor.

The actor is the AGV, which has ten state variables

(x,ω,V

,R, R

,J, ψ, T l,R

,a). The AGV actor tran-

sits to either ”stop” or ”run”. The two transitions in

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

472

Figure 10: AGV dynamics model.

this model ﬁre depending on the actors’ behaviors in

other models. We write the AGV’s dynamics only for

its motors and battery voltage in the scene ”run” as

shown in Fig.10, in order to temporally change the

values of its state variables during its motion. We

need not write the AGV’s dynamics in other models.

5.3.2 An AGV State Model

An AGV state model, shown in Fig.11 consists

of three scenes (”wait”, ”transport” and ”battery

change”) and an AGV actor. The scene ”wait” is a

scene in which the AGV is waiting for the parts A

to arrive at buffer 1. However, this model need not

include the actors of parts A and the buffer model.

We only write the AGV’s simple decision rules in the

scene ”wait” based on the current battery voltage of

the AGV.

5.3.3 A Transportation Process Model

This is a detailed model of the process of transporta-

tion, manufacturing, and assembly of parts A and B.

This model corresponds to the right side of the sin-

gle aspect model shown in Fig.9. The AGV transits

depending on its position x which temporally changes

according to the dynamics written in the AGV dynam-

ics model. For example, the transition between scene

Figure 11: AGV state model.

Figure 12: Actor-link setting window.

”route T-1” and ”process machinery” ﬁres when the

value of x becomes 50[m].

5.3.4 A Battery Change Process Model

This is a detailed model of the routes between buffer

1 and the battery station. This model corresponds to

the left side of the single aspect model. We write cer-

tain ﬁring conditions for transitions with respect to

the distance between buffer 1 and the battery station.

This model also need not consider other dynamics and

rules, like the transportation process model.

5.3.5 Actor-links and Multi-aspect Simulation

Finally, we deﬁne the links of the actors in order to

perform parallel simulation of the four STN models.

The STN GUI simulator makes it easy to deﬁne them.

Figure 12 is the user interface of the simulator for set-

ting the links. It shows that the four AGV actors in the

four STN models are regarded as same and they share

their state variables. The concept of actor-links re-

alizes the parallel simulation of the sub-STN models

considering their interactions, without making direct

connections between them using arcs and transitions.

5.4 Simulation and Results

We set ten sets each of parts A in the scene ”input”

and parts B in the scene ”buffer 2” and conduct par-

allel simulation. First, we observe the simulation re-

sult from the viewpoint of discrete-event systems. All

AGV actors are appropriately linked to each other

and move normally in the submodels. For example,

when the AGV stay in the scene ”route T-1” (it is

moving from buffer 1 to the process machinery) in

the transportation process model, it is also present in

the scenes ”run” in the AGV dynamics model and

”transport” in the AGV state and battery change pro-

cess models. By contrast, when it stays in the scene

”change”, it is also present in the scenes ”stop” in

the dynamics model and ”battery change” in the AGV

state and transportation process models.

Next, we observe the temporal changes in the state

variables as continuous systems expressed by the dif-

ferential equations. Figures 13 and 14 show the tem-

SCENE TRANSITION NETS SIMULATOR FOR MULTI-ASPECT MODELING OF DISCRETE-CONTINUOUS

HYBRID SYSTEMS

473

Figure 13: Temporal change of the position of the AGV

[m].

Figure 14: Temporal change of the battery voltage of the

AGV [V].

poral changes in the AGV’s position x and the bat-

tery voltage V

. These graphs show that the speed

of the AGV decreases according to the decrease in

the voltage of the battery. They also indicate that

the AGV goes to the battery station after the sixth

transportation of parts A and it changes the battery

at time t ≈ 250[s]. After changing the battery, the

speed of the AGV increases. In this way, we have con-

ﬁrmed that the proposed parallel simulation works ac-

curately, and this method enables us to observe the be-

haviors of the system from the viewpoint of discrete-

continuous hybrid systems.

6 DISCUSSION

In multi-aspect modeling, we ﬁrst construct a few

simple sub-STN models and integrate them. This

modeling procedure is very effective for modeling

complex systems. We have conﬁrmed that the di-

vision of a complex STN model using the concept

of multi-aspect modeling makes the working of STN

modeling easier through experiments. In addition,

the number of dynamics models we must write in

the STN model has also decreased. As a result, the

modeling method also simpliﬁes the modiﬁcation of

STN models. Multi-aspect modeling also contributes

to easy observation of the behaviors of complex sys-

tems. Each simple sub-STN model provides simple

and useful information to observers. The observers

easily obtain the necessary information by focusing

on appropriate submodels. For example, if an ob-

server wants to determine the AGV’s operating rate,

he obtains the required information by observing only

the behavior of the AGV dynamics model. On the

other hand, the AGV state model provides informa-

tion about the frequency of battery change. If an ob-

server wants to prove the efﬁciency of the transporta-

tion system, he should analyze the behavior of the

transportation process model. The concept of multi-

aspect modeling and the STN GUI simulator the au-

thors have developed will be more useful when we

verify more complex and larger-scale systems.

7 CONCLUSIONS

In this paper, the authors have proposed an STN mod-

eling concept called ”actor-link” that enables the shar-

ing the state variables of the actors. This simple con-

cept enables to construct complex layered and parallel

structures of STNs and perform multi-aspect model-

ing. The experiment with the case study of an auto-

mated transportation system using a battery-powered

AGV has shown that the proposed method and tool

assist users to easily construct multi-aspect models of

STNs and verify the behaviors of complex systems

from many different aspects.

ACKNOWLEDGEMENTS

This research was supported by Japan Productivity

Center, Grant-in-Aid for Productivity Research 2010.

ICINCO 2011 - 8th International Conference on Informatics in Control, Automation and Robotics

474

REFERENCES

de. Kleer, J. (1977). Multiple representations of knowledge

in a machanics problemsolver. Proceedings of 5th IJ-

CAI, pages 299–304.

Fishwick, P. A. (1991). Hetrogeneous decomposition and

inter-level coupling for combined modeling. Proceed-

ings of the 1991 Winter Simulation Conference, pages

1120–1128.

Kawada, S., Kawata, S., Kawai, S., Matsunaga, S., and

Watanabe, A. (1996). Some extensions of a scene

transition net by introducing actor transformation and

multi-aspect stn. Transactions of the Japan Soci-

ety of Mechanical Engineers, C62(599):2905–2912(in

Japanese).

Kawata, S., Kawada, S., and Watanabe, A. (1994a). The

discrete/continuous hybrid simulation using the scene

transition net. Proceedings of the First Asian Control

Conference(ASCC94), 1:567–570.

Kawata, S., Kawada, S., and Watanabe, A. (1994b). A man-

ufacturing system modeling using a scene transition

net. New Direction in Simulation for Manufacturing

and Communication, pages 86–92.

Murata, T. (1989). Petri nets: Properties, analysis and ap-

plication. Proceedings of the IEEE, 77(4):541–580.

Tateyama, T., Chin, T., Kawata, S., and Shimomura, Y.

Development and improvement of scene transition

nets(stn) gui simulator for discrete-continuous hybrid

systems. International Journal of CAD/CAM, 8(1).

Tateyama, T., Shimomura, Y., Mikoshiba, S., and Kawata,

S. (2010). Service ﬂow simulator using scene tran-

sition nets (stn) including satisfaction-attribute value

functions. Proceedings of the 15th Design for Manu-

facturing and the Lifecycle Conference - DFMLC2010

W. D. Kelton, R. P. S. and Sturrock, D. T. (2003). Simula-

tion with Arena. McGraw-Hill Science/Engineering.

SCENE TRANSITION NETS SIMULATOR FOR MULTI-ASPECT MODELING OF DISCRETE-CONTINUOUS

HYBRID SYSTEMS

475