MULTI-OUTPUT RANKING FOR AUTOMATED REASONING

Daniel K

uhlwein, Josef Urban, Evgeni Tsivtsivadze, Herman Geuvers and Tom Heskes

Institute for Computing and Information Sciences, Radboud University Nijmegen, Nijmegen, The Netherlands

Keywords:

Ranking, Automated theorem proving, Premise selection, Machine learning.

Abstract:

Premise selection and ranking is a pressing problem for applications of automated reasoning to large formal

theories and knowledge bases. Smart selection of premises has a signiﬁcant impact on the efﬁciency of auto-

mated proof assistant systems in large theories. Despite this, machine-learning methods for this domain are

underdeveloped. In this paper we propose a general learning algorithm to address the premise selection prob-

lem. Our approach consists of simultaneous training of multiple predictors that learn to rank a set of premises

in order to estimate their expected usefulness when proving a new conjecture. The proposed algorithm ef-

ﬁciently constructs prediction functions and can take correlations among multiple tasks into account. The

experiments demonstrate that the proposed method signiﬁcantly outperforms algorithms previously applied to

the task.

1 INTRODUCTION

Over the last two decades, the body of formally ex-

pressed knowledge has grown substantially. Formal

mathematics is becoming increasingly well-known,

used, and experimented with (Hales, 2008). Projects

like the formal proof of the Kepler Conjecture (Fly-

Speck) (Hales, 2005), the formal proof of the Four

Color Theorem (Gonthier, 2008), veriﬁcation of tiny

(but real) operating systems (Klein et al., 2009), and

the increased use of proof assistants for software

and hardware veriﬁcation (D’Silva et al., 2008) are

stimulating the development of interactive veriﬁca-

tion tools and interactive theorem provers (ITPs), and

the growths of the libraries of formal proofs, deﬁni-

tions, and theorems. Linked to this is the development

of strong automated theorem provers (ATPs), which

are used either independently to solve hard prob-

lems in suitable domains (McCune, 1997; Phillips

and Stanovsky, 2008), or assisting the interactive tools

(Urban, 2006; Meng and Paulson, 2008; Hurd, 2003;

Urban and Sutcliffe, 2008). In the usual setting, the

ATP is given a set of premises and a conjecture. The

ATP then has to prove that the conjecture is a logical

implication of the premises; or show that this isn’t the

case. In general, the more premises a problem has, the

bigger the search space for the ATP and the harder it

is to ﬁnd a proof.

With the continuing growth of formal knowledge

bases, the selection of relevant knowledge, when one

is presented with a new conjecture that needs to

be proven, becomes a concrete and pressing task.

Providing good solutions to this problem is impor-

tant both for mathematicians, and for existing ATPs

which typically cannot be successfully used directly

with hundreds or thousands of axioms. Experiments

with large theory benchmarks like the MPTP Chal-

lenge

, or the LTB (Large Theory Batch) division of

the CASC competition(Sutcliffe and Suttner, 2006),

showed that smart selection of relevant knowledge

can signiﬁcantly boost the performance of ATPs in

large domains (Urban et al., 2008; Urban et al., 2010).

Premise selection for automated theorem proving

can be seen as a ranking problem: Given a rank-

ing for a large set of premises, the ATP can try to

prove the conjecture by using only the highest ranked

premises. Several attempts to solving this problem

have been made (e.g. (Urban et al., 2010; Roederer

et al., 2009)). However, no state-of-the-art machine

learning techniques have been used.

In this paper, we develop new learning methods

for the selection of premises of new conjectures in

large formal theories. We apply our methods to avail-

able large libraries of formal proofs and compare

them with already existing algorithms.

http://www.tptp.org/MPTPChallenge

Kühlwein D., Urban J., Tsivtsivadze E., Geuvers H. and Heskes T..

MULTI-OUTPUT RANKING FOR AUTOMATED REASONING.

DOI: 10.5220/0003650400420051

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 42-51

ISBN: 978-989-8425-79-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

1.1 Formulation of the Problem as a

Machine-learning Task

Informally, we have to solve the following prob-

lem: Given a large knowledge base P of hundreds

of premises and a conjecture x, ﬁnd the premises

that are most relevant for proving x. Note that

this can be seen as a multi-label classiﬁcation prob-

lem where conjectures would correspond to examples

and premises to labels (Tsoumakas et al., 2010). We

present two different ways to approach this problem:

Let Γ be the set of all ﬁrst order formulas over a

ﬁxed countable alphabet, X = {x

| 1 ≤ i ≤ n} ⊂ Γ be

the set of conjectures, P = {p

| 1 ≤ j ≤ m} ⊂ Γ be

the set of premises, and Y : X × P → {0, 1} be the

indicator function such that y

= 1 if p

is used to

prove x

and y

= 0 if p

is not used to prove x

Binary Classiﬁcation. For each premise p ∈ P we

can construct a dataset D

= {(x, y

x,p

) | x ∈ X }. Based

on D

, a suitable algorithm can learn a classiﬁer

(·) : Γ → R which, given a formula x as input, can

predict whether the premise p is relevant for proving

x. Typically, classiﬁers give a graded output. Having

learned classiﬁers for all premises p ∈ P , the clas-

siﬁer predictions C

(x) can be ranked: the premises

that are predicted to be most relevant will have the

highest output C

(x). This approach to premise selec-

tion/ranking is proposed in (Tsivtsivadze et al., 2011).

Multi-output Ranking. We can also consider the

above problem as a label ranking task (see e.g.

(Fuernkranz and Huellermeier, 2011)): We assume

that for every conjecture x, there is a transitive, asym-

metric preference relation ≤

⊆ P × P such that for

all p, q ∈ P p ≤

q if and only if q is more relevant

for proving x than p. The goal is to predict this re-

lation. For each conjecture, we are given the output

vector y

= (y

x,p

, . . . , y

x,p

). Note that due to the na-

ture of our data we are concerned with bipartite rank-

ing (Agarwal, 2005), but the formulation stands for

real-valued y

x,p

as well. If we consider a matrix of di-

mension n ×m constructed with the output vectors of

all conjectures in the dataset, predicting each column

corresponds to a single classiﬁcation task as described

above.

Finally, the training set can be written as D =

{(x, y

) | x ∈ X }. Given the training set, our task is

to ﬁnd a ranking function f : Γ → R

such that for

each conjecture x ∈ X the ranking ≤

f (x)

⊆ P × P in-

duced by the function f is a good “prediction” of the

true preference relation ≤

⊆ P × P .

Differences to the Standard Ranking Setting. It is

interesting to note that the ranking problem described

above is somewhat different to standard ranking prob-

lems that are frequently encountered in information

retrieval, bioinformatics, natural language processing,

and many other domains. For example, a common

task in information retrieval is document ranking task.

Given a query we are interested in predicting the rank-

ing of some set of retrieved documents for the par-

ticular query. Drawing a parallel with the premise

selection task, given a conjecture we are interested

in determining a ranking of the premises so that the

premises that are most useful are ranked on top. How-

ever, there is a crucial difference: The datasets for

document ranking tasks (e.g. LETOR dataset

) con-

tain feature representations of the query and the doc-

uments as well as their rankings, while in our dataset

only feature representations of the conjectures and the

appropriate rankings of the premises (but not their

feature representations) are available

Therefore, the approach we take in the next sec-

tion can be informally summarized as follows. We

aim to determine the ranking of the set of premises for

a particular conjecture. However, because no feature

representation of the premises is available for learn-

ing we instead solve the problem by determining how

useful a particular premise is to prove a conjecture.

Once that score (rank) is determined we can induce a

total order over the set of premises that can be used to

prove the conjecture.

1.2 Organization

The remainder of the paper is organized as follows:

Section 2 describes the developed kernel algorithm

and the algorithms that have already been used in this

setting. An evaluation of the different methods can be

found in section 3. We discuss the results of the ex-

periments in section 4. In section 5, we argue about

the signiﬁcance and the impact of this work. Finally,

a conclusion is presented in section 6.

2 ALGORITHMS

In this section we present our framework for multi-

output ranking for premise selection as well as two

algorithms that have already been used for this prob-

lem. We will compare all introduced algorithms in the

experiments.

http://research.microsoft.com/users/tyliu/LETOR/

One example for such a problem is the cross-

veriﬁcation of a single proof within a large library where

we do not have access to the imported theorems.

MULTI-OUTPUT RANKING FOR AUTOMATED REASONING

2.1 Multi-output Ranking

We propose a method for multi-output ranking

(MOR) that is a relatively straightforward extension

of the preference learning algorithm described in

(Tsivtsivadze et al., 2010). We also note that the algo-

rithm is a generalization of the multi-output regular-

ized least-squares method and is not speciﬁcally tied

to the automated reasoning domain. It can be applied

to various problems in bioinformatics (e.g. protein

ranking), information retrieval (e.g. collaborative ﬁl-

tering), natural language processing (e.g. parse rank-

ing), etc.

Our method is based on the regularized least-

squares (RLS) (Rifkin et al., 2003) algorithm. This

choice is motivated by the fact that RLS has been

shown to perform comparably to state-of-the-art su-

pervised learning algorithms (e.g. SVM) (van Gestel

et al., 2004; Zhang and Peng, 2004) and has several

computational advantages, e.g. the fact that it can be

efﬁciently extended to handle multiple output predic-

tion problems. The standard version of the RLS al-

gorithm can be considered as as special case of the

following regularization problem known as Tikhonov

regularization (for a more comprehensive description,

see e.g., (Poggio and Smale, 2003)):

min

∑

i=1

l( f (x

), y

) + λk f k

, (1)

where l is the loss function used by the algorithm,

f : X → R is a prediction function, λ ∈ R

is a reg-

ularization parameter, and k · k

is a norm in a Re-

producing Kernel Hilbert Space (RKHS) (Schoelkopf

et al., 2001) deﬁned by a positive deﬁnite kernel func-

tion k. The loss function used with RLS for regression

problems is deﬁned as l( f (x),y) = (y − f (x))

. When

we restrict the prediction function f to be an element

F =



f ∈ R

| f (x) =

∞

∑

i=1

k(x, z

), β

∈ R,

∈ Γ, k f k

< ∞



(2)

then, by the Representer Theorem (see e.g.,

(Schoelkopf et al., 2001)), the minimizer of equation

(1) has the following form:

f (x) =

∑

i=1

k(x, x

), (3)

where a

∈ R for 1 ≤ i ≤ n and k is the kernel function

associated with the RKHS mentioned above.

We can also consider a loss function that considers

pairs.

This can be further speciﬁed by deﬁning a rele-

vance matrix W ∈ R

n×n

for the data points. For ex-

ample, we could have that [W]

i, j

= 1 for the differ-

ence between the predictions for x

, x

if they are rel-

evant for the learning task and 0 otherwise (Tsivtsi-

vadze et al., 2010). We get the following problem:

min

f ∈F

∑

i, j=1

[W ]

i j

((y

− y

) − ( f (x

) − f (x

))

+ λk f k

(4)

Instead of simply regressing the scores, our ex-

tension of the algorithm predicts pairwise preferences

among the output. We also show how to take infor-

mation about relevant data points that is shared across

multiple rankings into account. For all p ∈ P let

∈ F be a prediction function and let W

be a rel-

evance matrix. We write the minimization problem

min

,..., f

∑

i=1

∑

k, j=1

]

k j

((y

− y

)

−( f

) − f

)))

+ λk f

(5)

Since we consider all conjecture pairs as relevant,

we have that [W

]

k j

= 1 for all p

∈ P , 1 ≤ j,k ≤

n. Using the Representer Theorem we know that

each prediction function f

can be written as f

(x) =

∑

i=1

i,p

k(x, x

). Let A = (a

i,p

)

i,p

with 1 ≤ i ≤ n, p ∈

P , i.e. A is the matrix where each column con-

tains the parameters of one premise classiﬁer , K =

(k(x

, x

))

i, j

, 1 ≤ i, j ≤ n be the kernel matrix and let

Y = (y

x,p

)

x,p

, x ∈ X , p ∈ P . Similar to (Tsivtsivadze

et al., 2010), we can rewrite the minimization prob-

lem in matrix notation as

min



(Y − KA)

L(Y − KA) +λA



, (6)

where L is the Laplacian matrix of the graph deﬁned

by the relevance matrix W. To minimize (5), we take

the derivative with respect to A:

∂

∂A



(Y − KA)

L(Y − KA) +λA



= − 2KL(Y − KA) + 2λKA

= − 2KLY + (2KLK + 2λK)A

(7)

We set the derivative to zero and solve with respect to

A = (KLK + λK)

−1

KLY (8)

= (LK + λI)

−1

LY (9)

The last equality follows from the strict positive deﬁ-

niteness of K ∈ R

n×n

It is interesting to note that a special case of our

algorithm corresponds to multi-output regression, that

is when L = I. In later sections we refer to the learning

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

algorithm where L is constructed from W as MOR-

ALLPAIRS and use the naming MOR-REGRESSION

when L = I.

Using a square loss function leads to an efﬁcient

multi-output ranking solution, namely we obtain pre-

dictions for each output by inverting the kernel ma-

trix only once and therefore the complexity of the al-

gorithm is hardly increased compared to a standard

single output problem.

2.2 SNoW

SNoW (Sparse Network of Winnows) is a machine

learning toolkit (Carlson et al., 1999) which is used in

the MaLARea (Urban et al., 2008) system. MaLARea

using SNoW in na

ıve Bayes mode is currently 1.3

times stronger on the large-theory division of the

MPTP Challenge benchmark

than other automated

reasoning systems and meta systems.

SNoW is used mainly for natural language pro-

cessing tasks, and is designed to work efﬁciently in

domains where the number of features and targets is

very large, which is useful for large theories with their

large numbers of symbols and premises. SNoW im-

plements several learning algorithms (Winnow, Per-

ceptron, Na

ıve Bayes), and also comes with a pre-

processor for efﬁcient emulation of some ﬁrst-order

learning methods. An earlier preliminary evalua-

tion of the machine learning methods available in the

SNoW toolkit suggested using na

ıve Bayesian learn-

ing.

The setup for the training of SNoW is to select

some suitable features characterizing the conjectures,

and to try to learn the association of such features with

the premises occurring in their proofs. The output fea-

tures are the premises used in the proof of the conjec-

ture, in particular, their ranking given by the activa-

tion weights.

2.3 APRILS

APRILS is a ranking method which was used in the

Divvy system (Roederer et al., 2009). APRILS is

based on Latent Semantic Analysis (LSA), a tech-

nique for analyzing the relationships between docu-

ments, using the terms they contain (Deerwester et al.,

1990).

LSA is used to compute the relevance of premises

to a conjecture by treating the formulas as documents,

and the predicate and function symbols as the terms

they contain. The computation of premise relevance

http://www.tptp.org/MPTPChallenge/

using LSA is a three step process. First, a relation-

ship strength between every pair of symbols is com-

puted. An initial relationship strength is computed

based on the co-occurrences of the symbols in the for-

mulas, and the total number of formulas containing

the symbols. The ﬁnal relationship strength is com-

puted by repeatedly combining the existing relation-

ship strength with the relationship strengths between

each of the two symbols and each other symbol, i.e.,

taking into account transitive relationships between

symbols. Second, a relationship strength vector is

computed for each formula. The vector has an entry

for each symbol. A symbol’s entry is the sum, across

all other symbols, of the product of the relationship

strength between the two symbols, and the number

of occurrences of the other symbol in the formula (so

that other symbols that do not occur in the formula

make no contribution to the vector entry). Finally, the

relevance of each premise to the conjecture is com-

puted as the dot product of their symbol relationship

strength vectors.

3 EXPERIMENTS

In this section, we compare the rankings obtained

from MOR-REGRESSION, MOR-ALLPAIRS, SNoW

and APRILS. Our experiments are conducted on three

subsets of the Mizar mathematical library (MML)

We note that the MML was recently used to evaluate

the performance of ATP systems

. An implementa-

tion of the MOR algorithm in Python, and all datasets

are freely available at the authors website.

Each subset consists of several examples (conjec-

tures). For each conjecture we are given a bipartite

ranking of all premises, where the premises which

were used in the proof of the conjecture have rank

1, and the premises that were not used in the proof

have rank 0. We randomize the complete dataset and

use 90% for training and reserve 10% for testing pur-

poses. The goal is to learn to predict the ranking of

the premises for the unseen examples (conjectures).

In our experiments we use the following settings.

For simplicity and comparability of the results we

The MML contains today over 1100 formal mathemat-

ical articles, covering a substantial part of standard under-

graduate mathematical knowledge. The library has about

50000 theorems, proved with about 2.5 million lines of

mathematical proofs. Such proofs often contain nontrivial

mathematical ideas, sometimes evolved over decades and

centuries of development of mathematics and abstract for-

mal thinking. It is available at http://www.mizar.org

http://www.tptp.org

MULTI-OUTPUT RANKING FOR AUTOMATED REASONING

choose the “bag of symbols” feature representation

for SNoW and the MOR algorithms. The features

of a conjecture are the number of occurrences of the

symbols of the conjecture. I.e. the feature map φ is

deﬁned as φ : Γ → R

where n is the number of differ-

ent symbols in the whole data set (the cardinality of

the signature of Γ). Since APRILS only takes TPTP

input, we use this representation for the APRILS ex-

periments.

As the kernel function, we use the so-called Gaus-

sian kernel (Shawe-Taylor and Cristianini, 2004)

which is parameterized by a single parameter σ. It

is deﬁned as

k(x, x

) = exp



−

2σ

(hφ(x), φ(x)i

− 2hφ(x), φ(x

)i + hφ(x

), φ(x

)i)



(10)

with h·, ·i being the normal dot product on R

The kernel algorithm uses a 10-fold cross-

validation on the training set to select the optimal pa-

rameters λ, σ. Once the parameters are estimated we

train the algorithm on the complete training set and

evaluate the performance on the test set. SNoW is

used in na

ıve Bayes mode. APRILS has no parame-

ters.

Finally, to compute the performance of an al-

gorithm we create 100 randomized copies of each

dataset. Each copy is split into a test (90%) and a

training (10%) part. The AUC performance of the al-

gorithm on a copy is the average of the AUC of the

conjectures in the test set. The ﬁnal performance is

the average AUC performance over all 100 copies.

3.1 Performance Metrics

We present the performance measures used in the ex-

periments.

3.1.1 AUC

Our basic performance measure is the AUC (see e.g.

(Cortez and Mori, 2004)) - the area under the ROC

curve. It can be interpreted as the probability that,

given a randomly drawn positive example and a ran-

domly drawn negative example, the decision function

assigns a higher value to the positive example. Values

It has been demonstrated that suitable feature represen-

tation can signiﬁcantly boost the performance of existing

ATP techniques in large domains (Urban et al., 2008). Con-

structing an appropriate feature space for the learning al-

gorithm is an important and relevant task, which is outside

of the scope of this paper. We refer to (Tsivtsivadze et al.,

2011) for the discussion on feature representations that have

been previously used in automated reasoning systems.

http://www.cs.miami.edu/

∼

tptp/TPTP/SyntaxBNF.html

closer to 1 show better performance. The AUC mea-

sure is appropriate for evaluating the performance of

bipartite rankings.

Formally, let c be a classiﬁer, x

, .., x

be the out-

put of c on the positive examples and y

, .., y

be the

output on the negative examples. Then, the AUC of c

AUC(c) =

∑

(11)

where 1

= 1 iff ϕ is true and zero otherwise.

3.1.2 Wilcoxon Signed-ranks

We use the Wilcoxon signed-ranks test (Wilcoxon,

1945) to test whether the AUC difference between

two algorithms is statistically signiﬁcant. The

Wilcoxon signed-ranks test is a non-parametric sta-

tistical hypothesis test which ranks the differences in

performance of two classiﬁers for each data set, ignor-

ing the signs, and comparing the ranks for the positive

and negative differences. The exact deﬁnition is as

follows:

Let c

and c

denote the performance scores of

the two classiﬁers on the i − th of N data sets, and

let d

= c

− c

denote the difference. We rank the

differences according to their absolute values. In case

of a tie, average ranks are assigned. Let

∑

rank(d

) +

∑

rank(d

) (12)

−

∑

rank(d

) +

∑

rank(d

) (13)

and

T = min(R

, R

−

) (14)

For large values of N, the statistics

z =

T −

N(N + 1)

N(N + 1)(2N + 1)

(15)

is distributed normally. With α = 0.05 we can assume

that the ranking differences are not coincidental if z <

−1.96 (Dem

sar, 2006).

3.2 Datasets

The evaluation is done on three datasets extracted

from the large Mizar Mathematical Library using the

MPTP system.

3.2.1 The MPTP Challenge Dataset

The MPTP Challenge is a MPTP-based benchmark

established for large-theory automated reasoning in

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

2006. This is a small subset (subtree) of the Mizar

library leading to the general topological proof of the

Bolzano-Weiestrass theorem (Bancerek et al., 2001)

(formulated generally in terms of nets instead of

countable sequences), and can be seen as the basic

benchmark for premise selections algorithms. Ear-

lier experiments have shown that learning over this

dataset signiﬁcantly helps with premise selection for

ATP system (Urban et al., 2008).

The MPTP Challenge dataset consists of 211 con-

jectures. 341 different premises are used. The total

number of used premises is 1227 which gives an av-

erage of 5.82 used premises per conjecture.

Table 1: AUC Results for the MPTP Dataset.

Algorithm Av. AUC Std. Deviation

MOR-REGRESSION 0.85588 0.03457

MOR-ALLPAIRS 0.81466 0.03680

SNoW 0.78685 0.04663

APRILS 0.85478 0.02629

Table 1 shows the average AUC and the standard

deviation over 100 randomizations of all four algo-

rithms on the MPTP dataset. In ﬁgure 1, we see

the statistical signiﬁcance of the results. Two algo-

rithms are connected by a bold line iff the differ-

ence in their AUCs is insigniﬁcant. In this example

the AUC difference between APRILS and the MOR-

REGRESSION is insigniﬁcant.

0.65 1.0

MOR-REG.

APRILS

SNoW

MOR-ALLP.

Figure 1: Comparison of the AUCs on the MPTP Dataset.

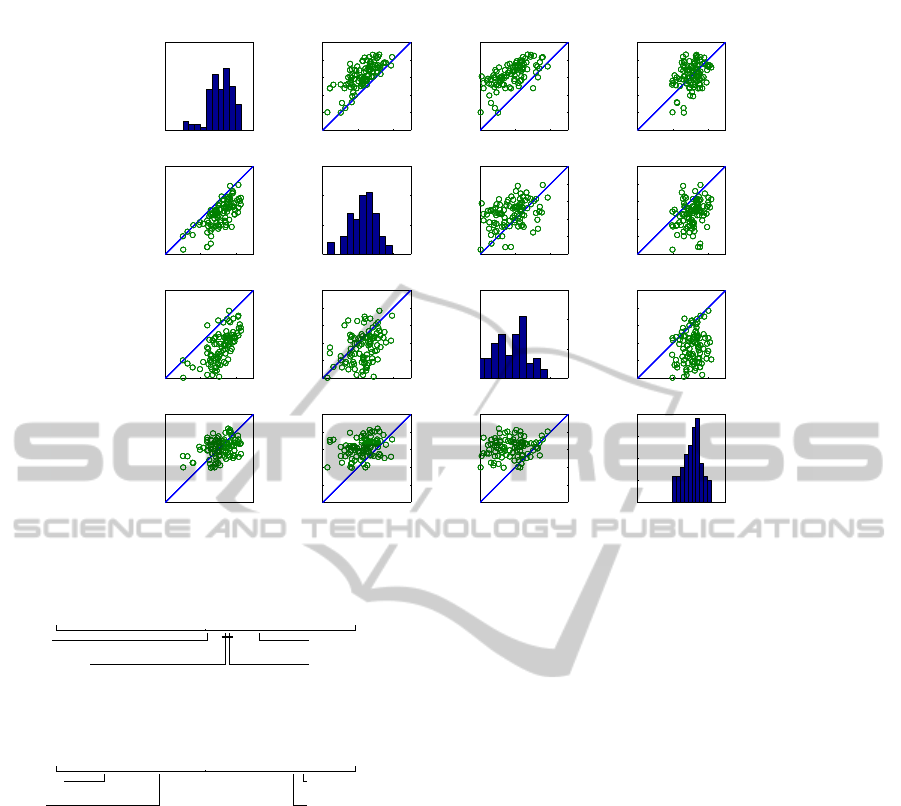
Figure 2 shows the detailed performance of the al-

gorithms on the MPTP dataset. The diagonal plots

show the histogram of the AUC performance on the

100 randomizations. The scatter plots show a pair-

wise comparison of the algorithms.

3.2.2 The Dataset of 370 Most used Mizar

Premises

This dataset was created in order to have the most bal-

anced positive/negative set of examples from MML.

Use of premises is generally quite sparse in mathe-

matics, leading generally to very unbalanced training

examples. This small dataset contains the premises

with the highest number of positive occurrences in

the MML, allowing experiments with methods that re-

quire reasonably balanced data.

This dataset consists of 351 conjectures with 525

different premises. The total number of used premises

is 2280, i.e. on average 6.50 used premises per con-

jecture.

Table 2: AUC Results for the 370 Dataset.

Algorithm Av. AUC Std. Deviation

MOR-REGRESSION 0.88868 0.02221

MOR-ALLPAIRS 0.84890 0.02809

SNoW 0.82823 0.03545

APRILS 0.85301 0.02194

Table 2 shows the average AUC and the standard

deviation over 100 randomizations of all four algo-

rithms on this dataset. In ﬁgure 3, we see the statis-

tical signiﬁcance of the results. In this dataset, the

AUC difference between the MOR-ALLPAIRS and

APRILS is statistically insigniﬁcant.

3.2.3 The Trigonometric Dataset

This is a dataset suitable for testing methods working

with structural input features. The examples are cre-

ated from a number of Mizar theorems about trigono-

metric functions. These theorems very often contain

the same set of symbols, for example {sin, cos, tan, =

, π, +, ∗}, and they thus mainly differ in the term and

formula structure.

The trigonometric challenge dataset consists of

530 conjectures with a total of 1020 different

premises. There are 5705 used premises altogether,

which gives an average of 10.76 used premises per

conjecture. Due to the formula structure and the num-

ber of premises, this dataset can be seen as the ’hard-

est’ of the three.

Table 3: AUC Results for the Trigonometric Dataset.

Algorithm Av. AUC Std. Deviation

MOR-REGRESSION 0.93977 0.01181

MOR-ALLPAIRS 0.92964 0.01674

SNoW 0.77078 0.02166

APRILS 0.70676 0.02288

Table 3 shows the average AUC and the standard

deviation over 100 randomizations of all four algo-

rithms on the trigonometric dataset. In ﬁgure 4, we

see the statistical signiﬁcance of the results. Here, all

AUC differences are statistically signiﬁcant.

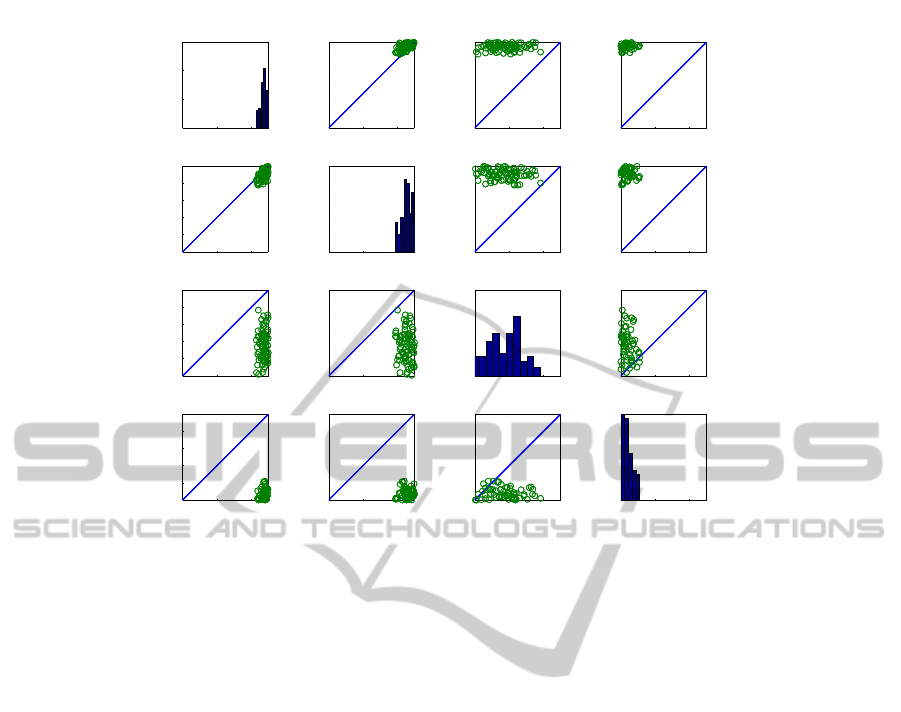
Figure 5 shows the detailed performance of the al-

gorithms on the trigonometric dataset. The diagonal

plots show the histogram of the AUC performance on

MULTI-OUTPUT RANKING FOR AUTOMATED REASONING

0.7 0.8 0.9

MOR−regression

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

MOR−allpairs

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

SNoW

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

APRILS

MOR−regression

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

MOR−allpairs

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

SNoW

0.7 0.8 0.9

APRILS

Figure 2: The results of the MPTP experiments.

0.65 1.0

MOR-REG.

APRILS

SNoW

MOR-ALLP.

Figure 3: Comparison of the AUCs on the 370 Dataset.

0.65 1.0

MOR-REG.

MOR-ALLP.

APRILS

SNoW

Figure 4: Comparison of the AUCs on the trigonometric

Dataset.

the 100 randomizations. The scatter plots show a pair-

wise comparison of the algorithms.

4 DISCUSSION

On all three datasets, the MOR-REGRESSION al-

gorithm outperform previously used methods for

premise selection. While the performance of APRILS

is not satisfactory on the largest dataset, both MOR-

ALLPAIRS and MOR-REGRESSION perform better

the more training data is available. It can be observed

that SNoW performs quite well on the 370 dataset, but

its average AUC score decreases again in the trigono-

metric dataset. We think that one reason for the good

performance of the MOR-REGRESSION algorithm is

the suitable formulation and use of a non-linear ker-

nel function, namely a Gaussian kernel. We also note

that the MOR-ALLPAIRS approach is in many cases

inferior to MOR-REGRESSION. Apparently, ranking

premises on conjectures does not lead to better per-

formance when the ﬁnal aim is to rank premises on

conjectures.

Furthermore, for estimating the ranking of all

premises the MOR algorithm requires time compa-

rable to training a single binary classiﬁer. Formally,

given p binary classiﬁcation tasks usually the training

time of the algorithm is multiplied by the number of

problems to be solved. For p < n, the by far most

computational demanding operation is the inversion

of the kernel matrix. However, training of the MOR

algorithm requires only O(n

) for p < n. This cor-

responds to the time necessary to train a single RLS

classiﬁcation algorithm.

The AUC together with 100 randomizations and

the Wilcoxon Signed-Ranks test seems like a very rea-

sonable measure to compare different ranking algo-

rithms, but it would also be interesting to test whether

high AUC scores actually translate to better ATP per-

formance. First experiments show that this is indeed

the case. Experimentally, we plugged the MOR-

REGRESSION algorithm into the MaLARea (Urban

et al., 2008) system, and compare its speed and

precision on the MPTP Challenge benchmark with

MaLARea running with naive Bayes (SNoW) as a

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

0.7 0.8 0.9

MOR−regression

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

MOR−allpairs

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

SNoW

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

APRILS

MOR−regression

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

MOR−allpairs

0.7 0.8 0.9

0.7

0.75

0.8

0.85

0.9

SNoW

0.7 0.8 0.9

APRILS

Figure 5: The results of the trigonometric experiments.

learning algorithm. In this ﬁrst test, the MOR-

REGRESSION algorithm solved more problems than

SNoW while needing approximately the same amount

of time. Furthermore, the number of problems solved

by the system after the sixth fast one-second run us-

ing the MOR-REGRESSION-based premise selection

outperforms any other non-learning (non-MaLARea-

based) system run in 21 hours on the MPTP Challenge

problems.

5 SIGNIFICANCE AND IMPACT

Trained mathematicians know a large number of the-

orems, solved problems, and tricks spanning many

mathematical areas. They have also developed an in-

tuition about the relevance of various parts of their

knowledge for various new problems. Existing au-

tomated deductive tools typically attack problems by

trying several human-programmed deductive strate-

gies, typically in an exhaustive and (theoretically)

complete way. This approach can be successful in

limited domains and/or for reasonably easy tasks, it

however does not scale to large complicated domains,

where the search space grows enormously.

Our approach in this situation is to complement

existing “theory-driven” implementations by develop-

ing suitable “data-driven” approaches for automated

reasoning. Once large numbers of formally expressed

theorems exist, they indeed complicate the exhaus-

tive search methods of existing deductive tools. On

the other hand, proofs of the large number of the-

orems provide a means to remedy the problem by

learning and re-using previously successful ideas for

steering the automated proof search methods. Suit-

able pre-selection of premises – and in particular their

ranking according to their expected proof relevance –

provides a way to efﬁciently combine existing ATP

systems with external “intuitive” advice. This can

lead to interesting combinations and feedback loops

between intuition-assisted deductive ﬁnding of facts,

and learning new intuitions from them. In this sense,

large formal theories provide an opportunity for cre-

ating new smart AI methods and systems. Suitable

learning methods for capturing the mathematical in-

tuitions – as developed in this work – are a necessary

prerequisite for building such smart mathematical as-

sistants.

6 CONCLUSIONS AND FUTURE

WORK

The contributions of this paper are threefold. First,

we present premise selection for automated theorem

proving as an interesting and challenging domain for

machine learning. Second, we propose a frame-

work for kernel based multi-output-ranking (MOR)

MULTI-OUTPUT RANKING FOR AUTOMATED REASONING

and make it, and the datasets that we use, publicly

available. Our MOR framework is much more com-

putationally efﬁcient compared to a binary classiﬁca-

tion approach. Note that although in this study we

are primarily concerned with the automated reason-

ing domain, our method is general enough to be ap-

plicable to ranking tasks in bioinformatics, natural

language processing, information retrial, etc. Third,

we compare our framework with existing premise se-

lection algorithms on three different datasets. The

experiments show that our method signiﬁcantly out-

performs the existing algorithms, in particular on the

harder problems.

In the future, we will ﬁrst extract and then uti-

lize feature representations of the premises in order

to improve the ranking performance of the proposed

algorithm. So far, we were only concerned with rel-

atively small problems. Our biggest dataset had only

1020 distinct premises. Eventually, we would like to

use our algorithm efﬁciently over datasets with tens

or even hundreds of thousands of premises. Our ﬁ-

nal goal is to incorporate the developed algorithm into

open source ATP systems which hopefully leads to

notable beneﬁts both in terms of accuracy and efﬁ-

ciency.

ACKNOWLEDGEMENTS

We acknowledge support from the Netherlands Orga-

nization for Scientiﬁc Research, in particular Learn-

ing2Reason and a Vici grant (639.023.604).

REFERENCES

Agarwal, S. (2005). A study of the bipartite ranking prob-

lem in machine learning. PhD thesis, University of

Illinois at Urbana-Champaign, Champaign, IL, USA.

AAI3182211.

Bancerek, G., Endou, N., and Sakai, Y. (2001). On the char-

acterizations of compactness. Journal of Formalized

Mathematics, 13(4):733–738.

Carlson, A., Cumby, C., Rizzolo, N., and

Rosen, J. (1999). SNoW user manual.

http://scholar.google.com/scholar?hl=en&btnG=Searc

h&q=intitle:SNoW+User+Manual#1.

Cortez, C. and Mori, M. (2004). AUC optimization vs. error

rate minimization. Advances in Neural Information

Processing Systems, 16:313.

Deerwester, S., Dumais, S. T., Furnas, G. W., Landauer,

T. K., and Harshman, R. (1990). Indexing by latent

semantic analysis. Journal of the American Society

for Information Science, 41(6):391–407.

Dem

sar, J. (2006). Statistical comparisons of classiﬁers

over multiple data sets. The Journal of Machine

Learning Research, 7:1–30.

D’Silva, V., Kroening, D., and Weissenbacher, G. (2008).

A survey of automated techniques for formal soft-

ware veriﬁcation. Computer-Aided Design of Inte-

grated Circuits and Systems, IEEE Transactions on,

27(7):1165–1178.

Fuernkranz, J. and Huellermeier, E. (2011). Preference

Learning. Springer Berlin Heidelberg, Berlin, Hei-

delberg.

Gonthier, G. (2008). Formal Proof – The Four-Color The-

orem. Notices of the American Mathematical Society,

55(11):1382–1393.

Hales, T. (2005). A proof of the Kepler conjecture. Annals

of Mathematics, 162(3):1065–1185.

Hales, T. (2008). A Special Issue on Formal Proof. Notices

of the American Mathematical Society, 55(11).

Hurd, J. (2003). First-order proof tactics in higher-order

logic theorem provers. Technical report, Design

and Application of Strategies/Tactics in Higher Order

Logics, number NASA/CP-2003-212448 in NASA

Technical Reports.

Klein, G., Elphinstone, K., Heiser, G., Andronick, J., Cock,

D., Derrin, P., Elkaduwe, D., Engelhardt, K., Kolan-

ski, R., Norrish, M., Sewell, T., Tuch, H., and Win-

wood, S. (2009). seL4: Formal Veriﬁcation of an

OS Kernel. In Anderson, T., editor, Proceedings of

the CICM Workshop on Empirically Successful Au-

tomated Reasoning in Mathematics, pages 207–220,

Big Sky, USA. ACM Press.

McCune, W. (1997). Solution of the Robbins Problem.

Journal of Automated Reasoning, 19(3):263–276.

Meng, J. and Paulson, L. C. (2008). Translating Higher-

order Problems to First-order Clauses. Journal of Au-

tomated Reasoning, 40(1):35–60.

Phillips, J. and Stanovsky, D. (2008). Automated Theo-

rem Proving in Loop Theory. In Sutcliffe, G., Colton,

S., and Schulz, S., editors, Proceedings of the CICM

Workshop on Empirically Successful Automated Rea-

soning in Mathematics, pages 42–54, Birmingham,

United Kingdom.

Poggio, T. and Smale, S. (2003). The Mathematics of

Learning : Dealing with Data. Notices of the Amer-

ican Mathematical Society, 50(5):537–544.

Rifkin, R., Yeo, G., Poggio, T., Rifkin, R., Yeo, G., and

Poggio, T. (2003). Regularized Least-Squares Classi-

ﬁcation, chapter 131-154. IOS Press.

Roederer, A., Puzis, Y., and Sutcliffe, G. (2009). Divvy:

An ATP Meta-system Based on Axiom Relevance Or-

dering. Automated Deduction - CADE-22, pages 157–

162.

Schoelkopf, B., Herbrich, R., Williamson, R., and Smola,

A. J. (2001). A Generalized Representer Theorem. In

Helmbold, D. and Williamson, R., editors, Proceed-

ings of the 14th Annual Conference on Computational

Learning Theory, pages 416–426, Berlin, Germany.

Shawe-Taylor, J. and Cristianini, N. (2004). Kernel Meth-

ods for Pattern Analysis, volume 47. Cambridge Uni-

versity Press.

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

Sutcliffe, G. and Suttner, C. (2006). The state of CASC. AI

Communications, 19:35–48.

Tsivtsivadze, E., Pahikkala, T., Boberg, J., Salakoski,

T., and Heskes, T. (2010). Co-Regularized Least-

Squares for Label Ranking, chapter 5, pages 107–123.

Springer.

Tsivtsivadze, E., Urban, J., Geuvers, H., and Heskes, T.

(2011). Semantic Graph Kernels for Automated Rea-

soning. In SIAM Conference on Data Mining.

Tsoumakas, G., Katakis, I., and Vlahavas, I. P. (2010). Min-

ing multi-label data. In Data Mining and Knowledge

Discovery Handbook, pages 667–685. editor.

Urban, J. (2006). MPTP 0.2: Design, Implementation, and

Initial Experiments. Journal of Automated Reasoning,

37(1-2):21–43.

Urban, J., Hoder, K., and Voronkov, A. (2010). Evaluation

of Automated Theorem Proving on the Mizar Mathe-

matical Library. Mathematical Software - ICMS 2010,

pages 155–166.

Urban, J. and Sutcliffe, G. (2008). ATP-based Cross-

Veriﬁcation of Mizar Proofs: Method, Systems, and

First Experiments. Mathematics in Computer Science,

2(2):231–251.

Urban, J., Sutcliffe, G., and Pudl

ak, P. (2008). MaLARea

SG1-Machine Learner for Automated Reasoning with

Semantic Guidance. Automated Reasoning, pages

441–456.

van Gestel, T., a.K. Suykens, J., Baesens, B., Viaene, S.,

Vanthienen, J., Dedene, G., de Moor, B., and Vande-

walle, J. (2004). Benchmarking Least Squares Sup-

port Vector Machine Classiﬁers. Machine Learning,

54(1):5–32.

Wilcoxon, F. (1945). Individual comparisons by ranking

methods. Biometrics Bulletin, 1(6):80–83.

Zhang, P. and Peng, J. (2004). SVM vs Regularized Least

Squares Classiﬁcation. In Pattern Recognition, 2004.

ICPR 2004. Proceedings of the 17th International

Conference on, volume 1, pages 176–179. IEEE.

MULTI-OUTPUT RANKING FOR AUTOMATED REASONING