AN APPROACH FOR COMBINING SEMANTIC INFORMATION

AND PROXIMITY INFORMATION FOR TEXT SUMMARIZATION

Hogyeong Jeong and Yeogirl Yun

WISEnut, Seoul, Republic of Korea

Keywords:

Latent semantic analysis, Proximity language model, Singular value decomposition, Text summarization.

Abstract:

This paper develops and evaluates an approach for combining semantic information with proximity informa-

tion for text summarization. The approach is based on the proximity language model, which incorporates

proximity information into the unigram language model. This paper novelly expands the proximity language

model to also incorporate semantic information using latent semantic analysis (LSA). We argue that this ap-

proach achieves a good balance between syntactic and semantic information. We evaluate the approach using

ROUGE scores on the Text Analysis Conference (TAC) 2009 Summarization task, and ﬁnd that incorporating

LSA into PLM gives improvements over the baseline models.

1 INTRODUCTION

The challenge of this paper is to generate an infor-

mative summary using sentence extraction. Ranking

sentences for extraction can be performed by the sen-

tence ranking function, which evaluates each sentence

against the document set, and gives a score repre-

senting its relevance for the summary. The ranking

function that we use is based on the proximity lan-

guage model, which uses physical proximity informa-

tion between terms in addition to term frequency in-

formation. We further extend this model by perform-

ing semantic smoothing using latent semantic analy-

sis (LSA).

2 RELATED WORK

Related work for our paper spans three areas: 1) pa-

pers that have adapted ranking functions for text sum-

marization; 2) those that employ the proximity lan-

guage model; and 3) those that use semantic smooth-

ing.

In the ﬁrst area, (Xie et al., 2004) performs text

summarization using a ranking function that is based

on various features of the sentence, such as its length

and location, while (Carbonell and Goldstein, 1998)

employs Maximal Marginal Relevance criterion to se-

lect best non-redundant sentences. Finally, (Mihal-

cea, 2004) uses graph-based ranking function based

on the HITS algorithm to assign scores for sentences.

The ranking function that this paper uses extends

traditional ranking functions to incorporate the prox-

imity language model (Zhao and Yun, 2009) and se-

mantic smoothing (Steinberger, 2004). The former

embeds syntactic information into the ranking func-

tion, while the latter embeds semantic information.

The proximity language model (PLM) extends the

traditional unigram language model to integrate term

proximity information. PLM embeds the proximity

information in a probabilistic model using Dirichlet

hyperparameters, rather than relying on a linear com-

bination of term frequency and proximity informa-

tion.

Meanwhile, latent semantic analysis (LSA) can be

used to incorporate semantic information. (Landauer

et al., 1998) explored using latent semantic analysis

for text summarization. In particular, we use ideas

in (Steinberger, 2004) to smooth our term importance

scores.

3 PROXIMITY LANGUAGE

MODEL

Proximity language model (PLM) forms the heart of

our ranking function, and is based on the unigram lan-

guage model (Zhao and Yun, 2009).

427

Jeong H. and Yun Y..

AN APPROACH FOR COMBINING SEMANTIC INFORMATION AND PROXIMITY INFORMATION FOR TEXT SUMMARIZATION.

DOI: 10.5220/0003650704190424

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 419-424

ISBN: 978-989-8425-79-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

3.1 Unigram Language Model

The unigram language model ﬁrst considers the vo-

cabulary set, V = { w

, w

, ..., w

|V|

}, for each word.

In the model, both the query q and the document d

are represented as vectors of counts for each word:

q =



, q

, ..., q

|V|



and d



i,1

, d

i,2

, ..., d

i,|V|



re-

spectively.

Then, a multinomial model is used, with param-

eters θ

= {θ

i,1

, θ

i,2

, ..., θ

i,|V|

}, with θ

i, j

representing

the probability of emission of word w

in document

. Using maximum likelihood estimation for the

multinomial distribution yields the estimator

i, j

(1)

with n

i, j

being the occurrence of the word w

document d

, and n

being the total occurrence of the

word in the collection.

3.2 Proximity Measure

The unigram language model is a simple model that

is based on the bag of words assumption. Under this

assumption, the only relevant information for a term

is whether or not it occurs in the document; i.e. its

position has no bearing on the model.

An intuitive way to extend the unigram language

model is to incorporate proximity information. For

example, we can give a higher score to a document

that contains the query terms in close proximity with

each other.

Typically, the distance is deﬁned as the minimum

number of words that occur between the query terms

in the document. If a query term does not exist in the

document, the length of the document is used for the

distance.

Proximity score for a term can then be calculated

using these term distance. One way uses the aver-

age distance among the query terms as the term prox-

imity score. While this approach has advantages in

that all of the distances are taken into account, not

all information may be equally relevant. For exam-

ple, suppose that the query is “computer mouse and

video games”, and that we are calculating proximity

score for the query term “mouse”. In this case, once

we have determined that the term “mouse” occurs in

close proximity with the term “computer”, its context

becomes somewhat clear, and the proximity informa-

tion between the term “mouse” and other query terms

becomes much less relevant.

Thus, another way to calculate term proximity

score is to use the minimum distance among the query

terms as the distance, which has shown higher accu-

racy scores empirically than using the average dis-

tance (Zhao and Yun, 2009).

We then perform an exponential transformationon

the term distance to convert it to a (0,1) scale. The

ﬁnal proximity score for a term q

is given as:

Prox(q

) = 1.5

−MinDist(q

)

(2)

3.3 Proximity Language Model

We are now ready to incorporate proximity informa-

tion to the unigram language model. In PLM, prox-

imity information for a term is incorporated as Dirich-

let priors (u

, u

, ..., u

|V|

), where u

= λProx(w

), and

λ is the Dirichlet parameter. Dirichlet priors reﬂect

our belief on how much the term proximity structure

should affect the term’s emission probability. The

maximum likelihood estimator in Equation 1 now be-

comes

i, j

+ λProx(w

)

∑

|V|

j=1

λProx(w

)

(3)

PLM further smoothes this estimator by us-

ing a collection language model p(·|C) to account

for unseen words in the document. The corre-

sponding Dirichlet priors {(µp(w

|C), µp(w

|C) , ...,

µp(w

|V|

|C)} are then applied on Equation 3, yielding

us the PLM estimator:

i, j

+ λProx(w

) + µp(w

|C)

∑

|V|

j=1

λProx(w

) + µ

(4)

4 SMOOTHED PROXIMITY

LANGUAGE MODEL

So far we have expanded the unigram language model

with the term proximity information. In addition, we

can employ latent semantic analysis (LSA) to smooth

the term frequency (Steinberger, 2004). Latent se-

mantic analysis relies on singular value decomposi-

tion, which extracts latent semantic information from

a term frequency matrix (Landauer et al., 1998).

4.1 Semantic Smoothing

We ﬁrst calculate term frequency matrix for each doc-

ument, with the rows consisting of the terms and

the columns consisting of sentences in the document.

Each entry t

i, j

of the matrix contains the number of

occurrences of the word w

in document d

divided

by the total occurrence of the word in the collection.

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

428

Traditionally, the term frequency information is fur-

ther augmented with the inverse document frequency

to incorporate word importance; however, in our case,

a similar role will be performed by semantic smooth-

ing.

With the term frequency matrix in hand, we per-

form singular value decomposition, which extracts or-

thogonal matrices with components in the latent se-

mantic space. A dimension in the latent semantic

space can be thought of as a topic for the document;

for example, it may take in terms “car” and “truck”

as input, and yield us a new dimension that is a lin-

ear combination of these two words, which may be

interpreted as a “vehicle”.

The output from singular value decomposition

consists of the orthogonal matrices U and V and the

diagonal matrix Σ. U gives component vectors for

each term in the latent semantic space, while V sim-

ilarly relates each document to the latent semantic

space. Meanwhile, Σ gives us the relative importance

of each latent semantic dimension.

We can now reﬁne n

i, j

, the number of occurrences

of the word w

in document d

, by exploiting the equa-

tion:

i, j

= n

× p(w

) (5)

where n

is the total number of words in docu-

ment d

, and p(w

) is the probability of the word w

in the collection. Next, we can use results from sin-

gular value decomposition to smooth p(w

) as in the

equation below, where d represents a dimension in the

latent semantic space.

p(w

) =

∑

p(w

|d)p(d) (6)

We must now estimate p(d) and p(w

|d), which

are needed to calculate p(w

). Relative weights for

each dimension are already given in the Σ matrix, and

p(d) can be estimated as

p(d) ∼ σ(d) (7)

As for p(w

|d), this can be estimated using a va-

riety of ways. The most obvious is to consider the

length of term vector, weighted by the importance of

each dimension, as a measure of its inﬂuence, which

results in the estimation:

p(w

|d) ∼

∑

(U( j, d)σ(d))

(8)

Now, using the semantically smoothed value for

i, j

gives us the SPLM estimator:

i, j

× p(w

) + λProx(w

) + µp(w

|C)

∑

|V|

j=1

λProx(w

) + µ

(9)

4.2 Ranking Function

The smoothed proximity language model gives us a

probability of each word occurring in a document.

We can then use these probability values to assign

scores for each query-document pair using the KL di-

vergence score as in (Zhao and Yun, 2009). The KL

divergence score represents the information loss in-

curred by using the query instead of the document,

and the closer this divergence score is to zero, the

closer the document is to the query. In document

ranking, we would thus choose documents with the

smallest KL divergence scores. The KL divergence is

deﬁned as:

(

) =

∑

(i)log

(i)

(10)

where

is the estimator for the query, and

the estimator for the document. After substitution of

the estimators, Equation 10 reduces to

∑

p(w

)log

q,i

p(w

|D)

+ logα

(11)

where θ

q,i

is the probability of the word w

occur-

ring in the query, and

∑

|V|

i=1

λProx(w

) + µ

(12)

5 TEXT SUMMARIZATION

Ranking functions that rank documents based on a

query can be used to rank sentences for text summa-

rization instead. When there is only one document in

the collection set, one can use the ranking function

in a straightforward manner to extract the most rele-

vant sentences. However, there may be multiple doc-

uments to be summarized, as may be the case when

generating a summary from multiple news articles.

5.1 Summarizing Multiple Documents

There are two approaches to rank sentences in this

case: the ﬁrst is to combine all the documents, and

then to compute the sentence relevance score against

the combined document; the second is sum the rel-

evance scores between the sentence and each of the

documents. We use the latter approach, as it has three

advantages. First, it is a scalable approach that can

easily admit additional documents. Second, one can

easily assign and readjust weights of different doc-

uments; for example, more weight may be given to

AN APPROACH FOR COMBINING SEMANTIC INFORMATION AND PROXIMITY INFORMATION FOR TEXT

SUMMARIZATION

429

more reputable sources. Finally, proximity informa-

tion can be better exploited when a sentence is com-

pared against each document separately.

5.2 Selecting Multiple Sentences

While the ranking function gives us the most repre-

sentative sentence, it provides no information for se-

lecting the best k sentences when there are multiple

sentences to be selected.

There exist many solutions to this problem. The

most basic solution is to select the k top scoring sen-

tences. However, doing so may result in selection of

redundant sentences. To help mitigate this problem,

one may only select sentences that have less than a

certain degree of overlap with every sentence in the

summary set (Kumar et al., 2009). More sophisticated

approaches, such as the MMR algorithm, formulate

the sentence selection problem as a search problem

that seeks to maximize an objective function which

gives credit for the relevance score, and penalizes for

overlap (Carbonell and Goldstein, 1998).

Experiments did not show many differences be-

tween these methods, and for our evaluation, we use

the aforementioned approach used in (Kumar et al.,

2009).

6 EXPERIMENTAL SETUP

The Summarization Task in the Text Analysis Confer-

ence (TAC) 2009 is an evaluation framework that pro-

vides a comparative analysis for computer-generated

summaries. Using this framework, accuracy scores

for short summaries can be compared among dif-

ferent algorithms. In the task, the challenge is to

generate summaries of up to 100 words from a col-

lection of 10 documents across 44 different topics

(Gillick et al., 2010). Then, the generated summary is

compared against model summaries using ROUGE-

2 measures, which gives recall and precision scores

based on whether bigrams in the generated summary

are also present in the model summary (Lin, 2004).

6.1 Methods for Comparison

We compare our approach against methods that only

use either PLM or semantic smoothing to see whether

employing both yields better results. In addition to

LSA, we compare semantic smoothing using latent

Dirichlet allocation (LDA) (Blei et al., 2003) and ran-

dom indexing (RI) (Sahlgren and Karlgren, 2005).

We thus consider the following approaches:

• Language Modeling (LM) only.

• Proximity Language Model (PLM).

• LM + latent semantic analysis.

• LM + random indexing.

• LM + latent Dirichlet allocation.

• PLM + latent semantic analysis.

• PLM + random indexing.

• PLM + latent Dirichlet allocation.

Sections 3-4 show the formulas used for the prox-

imity language model and PLM + latent semantic

analysis. The formulas used for other methods can

be adapted from these formulas, as we show.

6.1.1 Formula for the Language Modeling

Approach

Language modeling approach represents the most ba-

sic approach among our comparison methods. This

approachuses the estimator in Section 3.1, and the KL

divergence in Equation 10 can be used in a straight-

forward manner to derive scores for each sentence.

6.1.2 Formula for the Random Indexing

Approach

Random indexing represents another form of seman-

tic smoothing. Thus, employing random indexing in-

stead of LSA will affect equations in Section 4.1.

Running random indexing on the term-document

matrix will produce a term-context matrix. We can

perform LSA on this matrix, which will yield matri-

ces U andV and Σ that we can use in Equations 7-8 in

Section 4.1. Using these values will result in a mod-

iﬁed estimator in Equation 9. Sentence ranking can

then proceed as in Section 4.2. This method follows

the random indexing + LSA approach shown in (Sell-

berg and Jonsson, 2008).

This approach has advantages over LSA in perfor-

mance due to the fact that the term-context matrix is

of a reduced dimension. Computing the term-context

matrix takes an order of magnitude less time than

LSA, and thus, this approach leads to an improved

overall performance compared to regular LSA.

6.1.3 Formula for the Latent Dirichlet

Allocation Approach

Latent Dirichlet allocation is yet another form of se-

mantic smoothing. LDA can be used to analyze the

term-document matrix and provide latent topic proba-

bilities for each term. The topic probabilities for each

term can be substituted for p(w

|d) in Equation 6.

A weakness of using LDA in our semantic

smoothing framework is that LDA does not provide

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

430

topic weights. So instead of using tailored topic

weights, we use a constant value of 1 for p(d) in

Equation 6.

The updated p(d) and p(w

|d) values can be used

in Equation 9 to yield a modiﬁed estimator for the

LDA approach. Sentence ranking can then proceed as

in Section 4.2.

6.1.4 Baseline Model for Comparison

The baseline model that we compare against is the

HexTac baseline model provided by NIST, which uses

ﬁve human sentence extractors to manually select the

summary set (Genest et al., 2010). NIST states that

results from this model “provides an approximate up-

per bound on what can be achieved with a purely ex-

tractive summarizer”.

7 RESULTS

We ﬁrst compare text summarization results from our

model against reference and baseline models to show

advantages of the PLM + semantic smoothing ap-

proach. We then provide further experiments to show

that the PLM + LSA model is robust against parame-

ter variations.

Table 1: Results.

Algorithm F-score

Language Model (LM) .0954

Proximity Language Model (PLM) .0968

LM + latent semantic analysis (LSA) .0989

LM + latent Dirichlet allocation (LDA) .0993

LM + random indexing (RI) .0961

PLM + LSA .1054

PLM + LDA .0947

PLM + RI .1027

HexTac Baseline .1082

Figure 1: Comparison Results.

In Figure 1, we see that the performance of SPLM

is generally better than approaches that only utilize

the proximity language model or semantic smooth-

ing. The only exception is the PLM + LDA approach,

which may be explained by the fact that LDA does

not provide topics weights used in Equation 7.

The results show that SPLM can achieve a score

that is close to the HexTac baseline model, which is

considered to be an upper bound for extractive algo-

rithms such as ours (Genest et al., 2010).

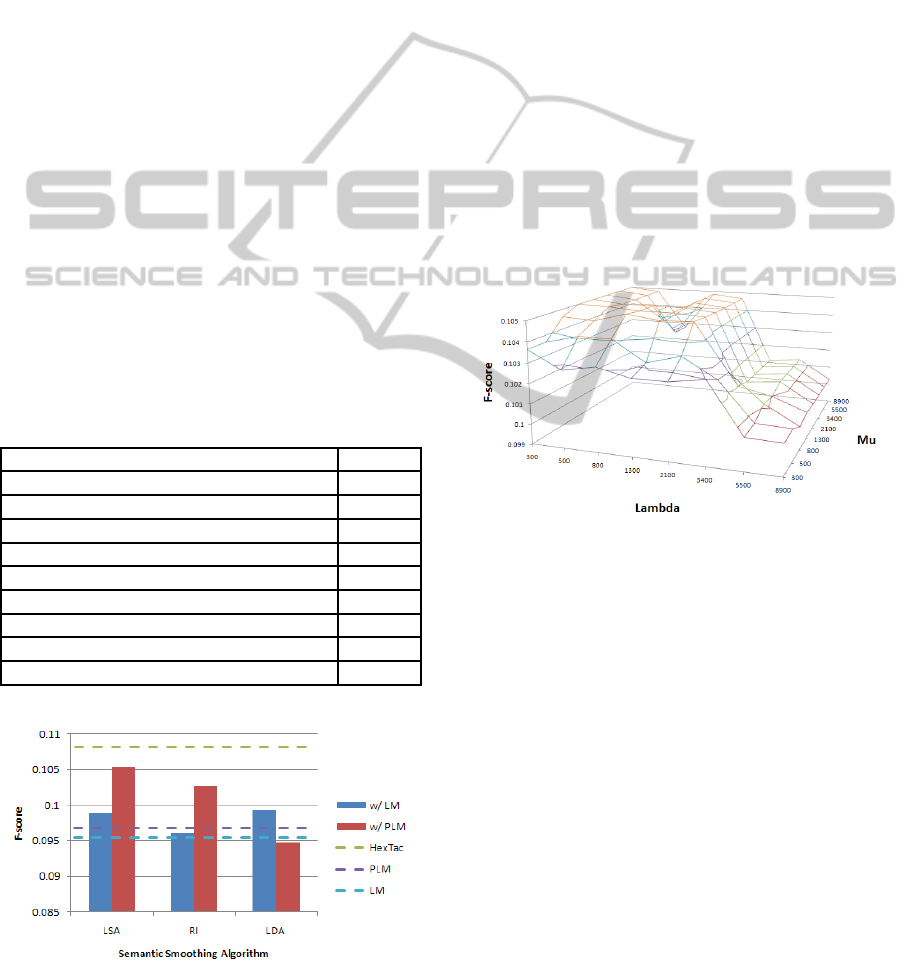
7.1 Robustness Testing Results

We may be wary of the choice of Dirichlet prior pa-

rameters λ and µ in Equation 9. If our results are too

sensitive to these parameters, then this limits applica-

tions of the approach in new domains. We varied the

values of λ and µ from 300 to 8900 to see whether

parameter variation would lead to a large change in

the F-score. Fortunately, we found these variations to

only cause a maximum of 4.8% change in the F-score.

Figure 2: Robustness Testing Results for the PLM + LSA

Approach.

8 CONCLUSIONS

The key contribution of this paper is in developing

an approach for combining semantic information with

proximity information for text summarization. The

approach is based on the proximity language model,

which expands the unigram language model to incor-

porate proximity information. This paper novelly ex-

pands the proximity language model to incorporate

semantic information using latent semantic analysis

(LSA). The proximity language model considers the

physical distance between terms to provide a better

ranking, while LSA applies semantic smoothing to

term importance. We argue that the presented ap-

proach achievesa good balance between syntactic and

semantic information.

AN APPROACH FOR COMBINING SEMANTIC INFORMATION AND PROXIMITY INFORMATION FOR TEXT

SUMMARIZATION

431

Upon evaluation of our approach, we ﬁnd that it

yields an improvement on models using just PLM or

LSA, and also comes close to what is considered the

limit for extractive systems. Moreover, further exper-

iments show that it is robust to parameter variations.

There still remains much room for improvement.

For achieving better results, we imagine having a bet-

ter sentence selection process, assigning variable doc-

ument weights, and using other forms of topic model-

ing for better semantic smoothing.

ACKNOWLEDGEMENTS

We would like to thank Jinglei Zhao for his invaluable

comments that helped to make this paper better.

REFERENCES

Blei, D. M., Ng, A. Y., and Jordan, M. I. (2003). Latent

dirichlet allocation. Journal of Machine Learning Re-

search, pages 993–1022.

Carbonell, J. and Goldstein, J. (1998). The use of mmr,

diversity-based reranking for reordering documents

and producing summaries. Proceedings of the 21st

annual international ACM SIGIR conference on Re-

search and development in information retrieval - SI-

GIR ’98, pages 335–336.

Genest, P., Lapalme, G., and Yousﬁ-Monod, M. (2010).

Hextac: the creation of a manual extractive run. Pro-

ceedings of the Second Text Analysis Conference,

Gaithersburg, Maryland, USA: National Institute of

Standards and Technology.

Gillick, D., Favre, B., Hakkani-Tur, D., Bohnet, B., Liu, Y.,

and Xie, S. (2010). The icsi/utd summarization system

at tac 2009. Proceedings of the Second Text Analysis

Conference, Gaithersburg, Maryland, USA: National

Institute of Standards and Technology.

Kumar, C., Pingali, P., and Varma, V. (2009). Estimating

risk of picking a sentence for document summariza-

tion. Computational Linguistics and Intelligent.

Landauer, T., Foltz, P., and Laham, D. (1998). An introduc-

tion to latent semantic analysis. Discourse Processes,

25(2):259–284.

Lin, C. (2004). Rouge: A package for automatic evaluation

of summaries. Proceedings of the workshop on text

summarization branches out (WAS 2004), pages 25–

26.

Mihalcea, R. (2004). Graph-based ranking algorithms for

sentence extraction, applied to text summarization.

Proceedings of the ACL 2004 on Interactive poster

and demonstration sessions, page 20.

Sahlgren, M. and Karlgren, J. (2005). Automatic bilingual

lexicon acquisition using random indexing of parallel

corpora. Journal of Natural Language Engineering,

pages 327–341.

Sellberg, L. and Jonsson, A. (2008). Using random index-

ing to improve singular value decomposition for latent

semantic analysis. In Proceedings of the Sixth Inter-

national Language Resources and Evaluation - LREC

’08.

Steinberger, J. (2004). Using latent semantic analysis in

text summarization and summary evaluation. Proc.

ISIM'04.

Xie, Z., Li, X., Di Eugenio, B., Nelson, P. C., Xiao, W., and

Tirpak, T. M. (2004). Using gene expression program-

ming to construct sentence ranking functions for text

summarization. Proceedings of the 20th international

conference on Computational Linguistics - COLING

’04, pages 1381–es.

Zhao, J. and Yun, Y. (2009). A proximity language model

for information retrieval. Proceedings of the 32nd in-

ternational ACM SIGIR conference on Research and

development in information retrieval, pages 291–298.

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

432