COULD TYRANNOSAURUS RUN FAST?

Mechanical Power Calculation for 15.7 m/s Tyrannosaurus Running

Yoshiyuki Usami

Institute of Physics, Kanagawa University, Rokkakubashi 3-25-1, Kanagawa-ku, Japan

Keywords: Tyrannosaurus, Locomotion, Theropod, Biomechanics, Mechanical power.

Abstract: Running ability of large bepidal theropod Tyrannosaurus is studied with the use of evolutionary

computational method. In 2002 Hutchinson and Garcia published a paper titled as "Tyrannosaurus was not a

fast runner" (Hutchinson and Garcia, 2002). They postulated an arbitrary mid-stance posture in running

motion, and calculated required muscle mass of the hind limb. This method can not tell information on

running speed, because it is a static method. Then, running speed of Tyrannosaurus could not be evaluated

quantitatively. We accomplished numerical simulation to obtain whole running motion of Tyrannosaurus

with the use of evolutionary computation method. As a result, we have obtained running motion of

Tyrannosaurus in a speed of 15.7 m/s within allowed parameters range. We have discussed on mechanical

power output of the running motion of Tyrannosaurus for the first time in this research area. As for a

problem of the simulation algorithm, there is room to improve simple evolutionary computation method

applied in the present work. Generally, a solution of evolutionary computation method falls into a local

minimum. However, finding the global minimum of the evaluation function i.e., velocity and vertical

acceleration are needed for this problem. Then, developing such an algorithm is left as the future problem.

1 INTRODUCTION

A problem of running ability of dinosaurs has not

been solved for many years. Both of the numbers of

theoretical researchers, and evidence of foot print

that show running motion have been quite limited.

Early estimation on running speed of Tyrannosaurs

was accomplished by Bakker and Paul in 1986 and

1988, respectively, based on morphological

consideration of muscle and limb structure (Bakker,

1986; Paul, 1988). Bakker and Paul proposed 45

mph and 40 mph running, respectively, which

correspond to the speed of 20 m/s and 17.9 (

≅

18)

m/s. These estimates are almost two times faster

than one of the humans at best. A monumental

qualitative study was achieved by Alexander with

the use of Froude number

⋅

, where v, h,

and g are velocity, characteristic length of leg and

gravitational constant, respectively. He employed

dynamic similarity hypothesis such that animal walk

or run in a dynamically similar fashion at the same

Froude number (Alexander 1976, 1985, 1989, 1996,

2006; Alexander and Jayes1983). With comparing

extant animal data, he found that relative stride L

has a relation with Froude number as,

3.0

)(3.2

⋅

(1)

where L

st,

h, v and g are the stride length which is a

distance between two successive falls of the same

foot, and hip height, velocity, and gravitational

constant, respectively (Alexander 1976). Alexander

proposed that the hip height h can be estimated from

foot print of dinosaurs as h=4FL, where FL is foot

length. Since then, many improvements have been

added to this expression. (Gatesy and Biewener

1991; Russell and Beland 1976; Thulborn 1981,

1989, 1990; Rainforth and Manzella 2007; Wallace

and Brooks, 2003). Recently, Rainforth and

Manzella re-analyzed this factor using 24 specimens

from different dinosaurian groups, and concluded

that speed estimation could be incorrect by a factor

of two (Rainforth and Manzella, 2007).

From fossilized foot print remains two evidence

of large dinosaurs running motion have been

reported. Farlow and Day et al. reported that 11.1

m/s and 8.11 m/s running evidence of medium and

large size bipedal theropod is obtained, which are

Usami Y..

COULD TYRANNOSAURUS RUN FAST? - Mechanical Power Calculation for 15.7 m/s Tyrannosaurus Running.

DOI: 10.5220/0003652100130022

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 13-22

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

calculated using Eq.(1) (Farlow, 1981; Day et al.

2002). Although the absolute value of running speed

has to be re-considered with care, foot prints show

that bipedal theropod was a fast runner with

comparable to human.

In 2002 Hutchinson and Garcia published a

paper titled as "Tyrannosaurus was not a fast

runner" (Hutchinson and Garcia, 2002). They

accomplished static calculation in which required

muscle mass is calculated for an arbitrary chosen

mid-stance posture in running motion. The result

yields that 43 % muscle mass is required for one

hind limb of Tyrannosaurus. On the other hand,

computer aided mass property study revealed that

the value is 16.0 % for MOR555 (Bates et al. 2009),

14.2 % for MOR 555 (Hutchinson et al. 2007), 14.4

% for BHI3033 (Bates et al. 2009). The abbreviation

stands for Museum of Rockies, and Black Hills

Institute, respectively. Then, Hutchinson concluded

that Tyrannosaurus was not a fast runner.

In 2004 Hutchinson re-evaluated this value, and

obtained a result that 21 % muscle mass is required

for one hind limb of Tyrannosaurus (Hutchinson

2004b). Recently, Gatesy et al. calculated the value

for various mid-stance postures (Gatesy et al. 2009).

The methodology is the same with Hutchinson and

Garcia's, then, the speed estimation is heuristic. The

results are considered as medium speed running is

possible, because 18.3 (~1.87× 9.8) m/s

vertical

acceleration is allowed in their estimation for static

postures.

In our recent studies, re-consideration of

involved parameters leads to almost two folds error

in the estimation of required muscle mass (Usami,

2011a-c). Figure 1 displays 3D bone structure of

BHI3033 specimen taken by us using 3D laser

scanner FARO LS. Recently, Sellers and Manning

accomplished numerical simulation study for this

problem. They obtained that about 8~9 m/s running

is possible for Tyrannosaurus (Sellers and Manning,

2007).

Figure 1: 3D bone structure of BHI3033 specimen taken

by using FARO co. LS.

Instead of this methodology, this paper presents a

result of calculation of mechanical power in running

motion of Tyrannosaurus. This metho-dology

excludes uncertainty of many biomechanical

parameters. Then, this evaluation is superior to the

static evaluation in evaluating running speed of

Tyrannosaurus.

2 DYNAMICAL CALCULATION

OF THE LOCOMOTION OF

TYRANNOSAURUS

This section describes the method of numerical

simulation of Tyrannosaurus running motion.

2.1 A Solid Object Approximation and

Calculation of the Moment of the

Force

Running motion is a periodic one, hence, expressing

time change of each joint angle by Fourier

expansion series is appropriate. Validity of this

method was checked in advance on human

locomotion. The motion capture of human running

motion was accomplished by the combination of

optical measurements and the use of force plate on

the ground. These data were analyzed by the reliable

system VICON (Vicon Motion Systems). Next, time

change of each joint angle is expressed by Fourier

expansion series. Convergence within 1 % accuracy

is checked by taking into account of 5

order Fourier

expansion. Thus, an expression of 5

order Fourier

expansion is a good method to describe the periodic

motion of each joint. For i-th joint angle

)(t

the

expansion is expressed as follows,

"++++= )sin()0sin()(

1100

iiiii

tatat

δωδθ

(2)

where

a ,

are the amplitude and the phase of j-

th order of expansion series for i-th angle,

respectively. The

is angular velocity. The

segment structure of Tyrannosaurus is the same of

Hutchinson and Garcia’s model shown in Fig. 2(a)

(Hutchinson and Garcia, 2002). To study time-

dependent dynamics a solid object model is used to

describe the motion of Tyrannosaurus limb.

Namely, the model Tyrannosaurus moves as one

solid object for the external force

)(rF

as the

following equations,

)(

rFgm

bodybody

+−=

(3a)

)(

rFr

Φd

⋅=

(3b)

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

Figure 2: (a) Segment model of Tyrannosaurus of

Hutchinson and Garcia (Hutchinson and Garcia, 2002). (b)

A free-body diagram. Using (b) the torque at a joint can be

calculated from foot segment, sequentially.

where

and

are the position vector of the

center of mass and the rotational angle of the object,

respectively. The calculation is achieved in the

sagittal plane, i.e., two-dimensional space x

(horizontal) and y (vertical). I, g and

are the

momentum of inertia of Tyrannosaurus,

gravitational constant, and the position vector to the

point of the force, respectively. The term

body

gm− expresses that gravitational force acts in

vertical direction y. The value of inertia I is chosen

as I=19000

mkg ⋅ in our work with the references

(Hutchinson et al. 2007; Bates et al. 2009). A solid

object model is simple, however, it is known to

express dynamics of moving object with many

degree of freedom (Usami et al. 1998).

For calculating joint torque, or moment of the

force about joint, a free-body diagram analysis is

applied as shown in Fig.2(b). For example, let us

call the foot segment as segment “1” , and define the

mass and the moment of inertia as m

and I

respectively. Then, the equations of motion for

translation and rotation become as follows in (x, y)

plane,

11121

amgmFF

=−−

(4a)

11212211



IMMFxFx

=−+×−×

(4b)

where

and

are the force from downside

segment, the force from upper segment and

acceleration, respectively. For rotational motion,

and

are the vectors from the center of mass

of 1-th segment to the point acting force

and

and M

are the moment of force between the 0-th

and 1-th, 1-th and 2nd segments, respectively. For

the case of 1-th segment

corresponds to the

ground reaction force.



is time derivative of

angular velocity. Putting known terms



and M

into Eq.(4) yields unknown terms

and

. Thus, the moment of force acting to upper

segment is obtained, subsequently. In the usual

motion the term



and

are negligible. Then,

these terms are set as zero in our calculation. The

parameter for ground reaction is described in our

paper in detail (Usami, 2011c).

2.2 Evolutionary Computation Method

Solid Object Approximation for the

Motion of the Whole Body

Searching the optimal Fourier coefficient

Eq.(2) for running motion is the next task. The other

parameters are fixed in the simulation.

Computational method for obtaining the optimal

solution in many degree of freedom is usually not an

easy task. So, a variety of approximation methods

have been proposed in many research areas. One of

the famous and well studied methods is the genetic

algorithm (GA) (Fraser 1970; Holland 1975;

Goldberg 1989). A vast number of studies has been

published in many research areas concerning to GA.

This method is based on an idea of gene evolution

observed in the actual life system. In this method

digitized virtual genes are introduced, and its

evolution is simulated. The virtual gene falls into the

stable state in which a value of evaluation function

has the local minimum. On the contrary, the

introduction of virtual genes is not necessary in the

present study. So, looking for another convenient

approximation method is appropriate. Another

approximation method for obtaining near optimal

solution is the evolutionary computational method

(Sellers and Manning 2007; Usami 1998; Fogel

1995). This method is known as well as genetic

algorithm method on searching near optimal

solution. This method does not introduce digitized

virtual gene, but change the parameters of the

system directly. A value of the evaluation function

converges into the local minimum rapidly, and the

result is usually satisfactory. Then, we use

evolutionary computational method for this problem.

COULD TYRANNOSAURUS RUN FAST? - Mechanical Power Calculation for 15.7 m/s Tyrannosaurus Running

At first, we create several typical patterns of

running motion at hand using 3D software 3dsmax

(Autodesk co.). The typical patterns include various

motions from flexed one to upright one. Next, we

apply dynamical simulation described above. Our

method does not introduce virtual gene as appeared

in the usual genetic algorithm, but, changes

parameters itself in the Eq.(2).

Let us call the initial set of parameters as the

initial parent. The initial parent makes 2000 children

whose parameters are slightly different from the

initial parent. The different parameters are generated

by a random algorithm. The running simulation is

applied for the 2000 children, and the best

performance child is selected among those. Then,

the best performance child becomes the parent in the

next generation. Thus, near optimal solution on

running motion is obtained as a result of the

evolutionary computation scheme. The term "best

performance" is determined by the introduction of

the evaluation function. It is discussed in the next

section in detail.

3 MECHANICAL POWER IN

TYRANNO-SAURUS RUNNING

MOTION

In this section result of calculation of mechanical

power output for Tyrannosaurus running motion is

presented.

3.1 Moment of Force, Angular Velocity

and Mechanical Power

In the simulation, we have carried out calculation in

a range of cycle time T=0.5~0.7(s). Many different

running patterns are appeared in the simulations with

different initial conditions. Let us define ground

reaction force multiplier factor G as

GgmF

body

−= , where F and

body

m is ground

reaction force in the vertical direction and the total

mass of Tyrannosaurus. Then, biomechanical

knowledge tells that moderate speed running motion

is realized when 1<G<2, and fast running is realized

when 2<G<4. If G exceeds 4, the running motion is

said to be beyond reality.

As for the evaluation function in the optimization

process, we have tried several types of evaluation

function such as vertical acceleration, running

velocity and the product of velocity and vertical

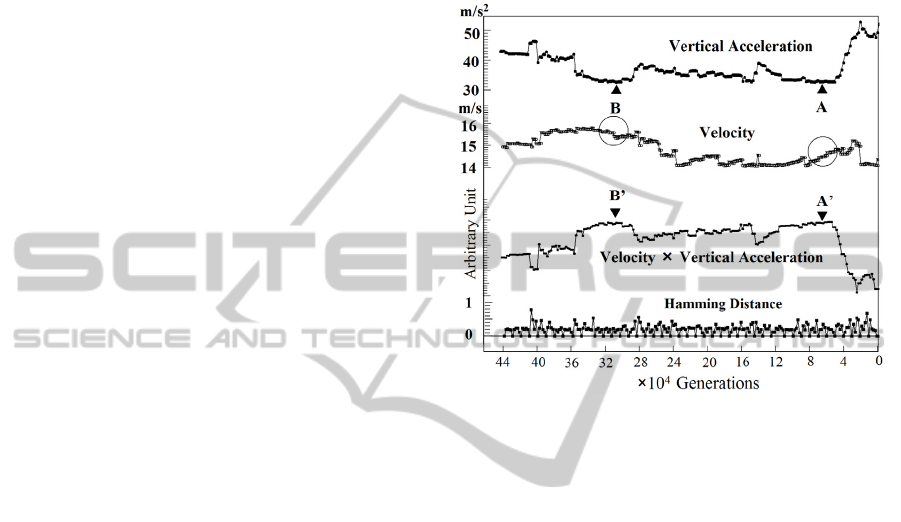
acceleration, etc. Figure 3 displays a successful case

that local minimum of vertical acceleration appeared

in the simulation, which is shown as A and B. A and

B give the same value of the local minimum in the

simulation. However, corresponding velocities are

different as shown by the circle in Fig.3. Then, B’

gives a slightly better solution in the criteria of

velocity times vertical acceleration.

Figure 3: An example of simulation of

104.4 ×

generations. Vertical acceleration, velocity,

velocity

vertical acceleration, and Hamming distance of

subsequent generations are plotted.

Hamming distance for subsequent generations is

also plotted in Fig.3. This data shows that small

change of the parameters affects pattern of

locomotion, which leads to the change of vertical

acceleration and running velocity.

In the computer simulation most of the examples

yielded bad results, namely, there was no

appropriate local minimum. Or, in many cases

vertical acceleration increased in the simulation of

the evolution algorithm. Figure 4 displays such an

example. It started from a slightly different initial

condition from the one of Fig.3. Thus, a result of

simulation depends on the choice of the initial

condition. Then, we have carried out many running

simulations for searching a solution which gives the

lowest vertical acceleration and the fastest running

velocity.

Generally, an evolution algorithm is able to

obtain a local minimum of evaluation function.

However, we have to obtain the global minimum of

the evaluation function, i.e., running speed and

vertical acceleration. Thus, searching efficient

algorithm, which brings an appropriate solution for

this study is left for us as the future problem.

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

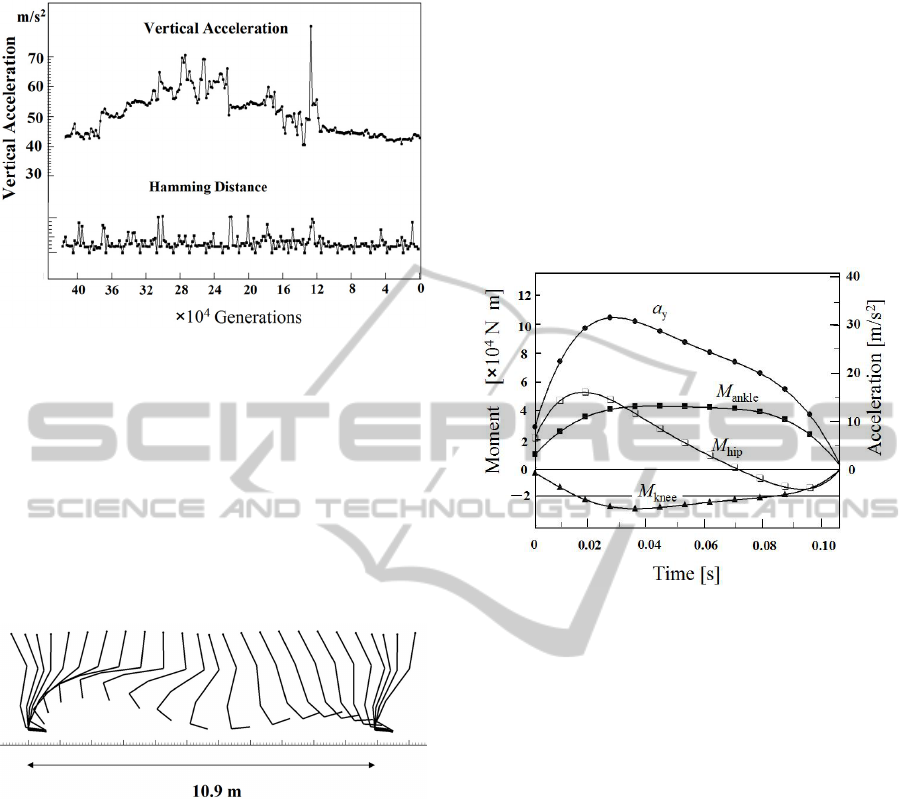
Figure 4: Another example of running simulation, which is

failed to obtain a local minimum.

Furthermore, it is noted that the present

evolutionary algorithm is rather primitive.

Developing better algorithm to search the global

minimum would shed light on this problem.

However, it is also noted that running motion in the

simulation is very sensitive to a small change of

parameters. The choice of the evaluation function,

i.e., running velocity, vertical acceleration, or the

product of those is also not a simple problem.

Figure 5: Stick diagram of the fastest running motion in a

speed of 15.7 m/s appeared in our numerical simulation.

Then, as a whole finding the global minimum of

the system is said to be a difficult problem.

In the range of cycle time T=0.5~0.7(s) we have

searched solution with 1<G<4. In this range of G we

have obtained solution of running speed v=8.0~15.7

(m/s). Then,

=15.7 (m/s) is the maximum speed

appeared in our numerical simulation with

=3.2,

which is valid in biomechanical knowledge. Figure 5

displays stick diagram of running motion of

v =15.7

(m/s). The cyclic time is T=0.69 (s) in this case,

and the stride length is 10.9 (m) as appeared in

Fig.5. Figure 6 shows vertical acceleration

, and

moment of the force of the hip joint

hip

, knee joint

knee

M and ankle joint

knee

M . The contribution of

the toe joint is omitted because the ankle extensors

could have been producing most of the required toe

joint moments (Hutchinson 2004a, 2004b). We

observe that the maximum of vertical acceleration is

31, which yields multiplier factor G=3.2. The

maximum of the moment of force is 5.1 ×10

(N・

m). Note that the center of mass is located at the hip

joint in this calculation. It is known that the center of

mass of Tyrannosaurus is located 0.3-0.7m cranial

based on mass property study (Bates et al., 2009:

Gatesy and Hutchinson, 2009).

Figure 6: The vertical acceleration

, and moment of

force of each joint

where i=hip, knee and ankle.

It should be noted that these may change the

value of the moment of force by a factor of two

based on our works (Usami 2011b, 2011c).

Corresponding angular velocity of each joint is

plotted in Fig.7. Then, mechanical power output of

each joint

is calculated using the relation.

iii

⋅

. The

, the sum of each power

anklekneehiptotal

PPPP

, and vertical acceleration

is plotted in Fig.8. The moment of force of the hip

joint M

hip

changes its sign from plus to be minus in

Fig.6, then,

hip

and

Total

shows the double peak.

In the data of biomechanical study, vertical

acceleration usually shows the sine curve with time.

It is observed that

a is slightly different from

sine curve in Fig. 6 and Fig.8. This is mainly due to

the fact that each part of the body is smoothly

connected. And, it prevents sudden change of

acceleration.

Our

Tyrannosaurus model is only made by leg

part, then there is no room to absorb large change of

acceleration. Each body part such as neck, trunk and

tail would absorb such large change of acceleration

COULD TYRANNOSAURUS RUN FAST? - Mechanical Power Calculation for 15.7 m/s Tyrannosaurus Running

Figure 7: Angular velocity of each joint ω

, where i=hip,

knee and ankle.

Figure 8: Mechanical power for i-th joint Pi, the sum and

the vertical acceleration

in Tyrannosaurus. Then, we correct this discrepancy

by giving sine function for vertical acceleration in

the calculation of Fig.8. The result is shown in Fig.9,

in which the maximum value of acceleration is set

equal to the one of Fig.6. Namely, we give the sine

function for vertical acceleration, and re-calculate

The maximum power of

total

is obtained as

3.89×10

(Watts) in the stance phase of 15.7 (m/s)

running. Contribution of the power of the toe joint is

omitted as the same reason discussed in the

evaluation of the moment of force in Fig.9.

3.2 Mechanical Power per Kilogram of

Muscle Mass, and Comparison with

the Data of Extant Animals

For the evaluation of running ability, the mechanical

power per kilogram muscle is calculated, and

compared to the other data. The value of

total

in Fig.

Figure 9: Each Pi is re-calculated as the vertical accele-

ration being set as sine function for Fig.6.

9 is divided by the muscle mass of a leg. As for

muscle mass of leg, 16 % of the total mass are

employed. 16 % muscle mass per leg is the

maximum ratio derived from recent mass property

studies (e.g. Bates et al. 2009, Hutchinson et al.

2007).

The result is shown in Fig.10. For the

comparison, the data of extant animal is introduced.

Pontzer et al. recently suggested that endothermy is

plausible for large bipedal dinosaurs (Pontzer et al.

2009). And at present, birds are widely recognized

as flying theropod dinosaurs. These may imply high

activity in locomotion for such dinosaurs. The

mechanical power output of muscle has been

reported in many articles. Askew et al. reported that

a power output for one individual of blue-breased

quail (Coturnix chinensis) was 530 W/kg (Askew et

al. 2001a, 2001b). They also calculated the power

requirements during takeoff flights in four other

species in the family Phasianidae, one species of

hawk, several species of hummingbird and two

species of bee. Remarkably, they concluded that,

over a broad range of body size (0.0002–5 kg) and

contractile frequency (5–186 Hz), the myofibrillar

power output of flight muscles during short maximal

bursts was very high as 360–530W/kg (Askew et al.

2001a, 2001b). On measurements on bundles of

muscle fibres

in vitro Askew and Marsh reported

that the highest was 433 W/kg (Askew and Marsh,

2001a).

Smaller values were reported by Dial and

Biewener as 119 W/kg for pegion during takeoff

(Dial and Biewener, 1993). For Australian rocket

frogs (Litoria nasuta) James and Wilson reported

that an average power output during takeoff in

jumping varied between individuals within a range

from 318 to 747 W/kg (James and Wilson, 2008).

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

Figure 10: The power per kilogram of muscle mass and

the data for extant animal.

Wilson et al. reported high power output of 900

W/kg (Wilson et al., 2000). The others are in a range

of 225-550 W/kg (225-550 W/kg by Marsh and

Alder 1994; 360 W/kg by Lännergren et al. 1982).

On mammals, high power output was observed in

kangaroo jumping as 495-640 W/kg by McGowan et

al. (McGowan et al. 2005). They suggested that back,

trunk and tail musculature likely play a substantial

role in contributing power during jumping. Inclusion

of this musculature decreased the value to 452 W/kg

for the power output.

To sum up, animal's mechanical power output

high values of several hundreds W/kg have been

widely observed in different taxa. Relation with the

result obtained in contractile property study of

bundles of muscle fibre is left as future works.

Currently, it is not solved yet how an animal can

generate such high mechanical power output.

Remarkably, Lappin et al. reported that mechanical

power of mandibulae muscles of frog reached to

9600 W/kg for (Lappin et al., 2006). It is noted that

lower values in different taxa have been widely

reported as 107 W/kg for mouse (James et al. 1995),

110-122 W/kg for dolphin (Gray, 1936; Weis-Fogh

et al., 1977). As a conclusion, these values permit

for

Tyrannosaurus to run in a speed of 15.7 (m/s).

4 CONCLUSIONS

In 2002 Hutchinson and Garcia doubted fast running

ability of

Tyrannosaurus for the first time

(Hutchinson and Garcia, 2002). Since then, large

bipedal theropod such as

Tyrannosaurus has been

considered as a slow runner. Sellers and Manning

studied this issue in 2007, and published a result that

8~9 (m/s) running is possible. However, parameters

used in the simulation was not well described. Then,

it is difficult to check their result. Quite recently, we

have studied this issue in detail (Usami, 2010a-c). In

the study, it is revealed that parameters used in

Hutchinson et al.'s studies (Hutchinson and Garcia,

2002; Hutchinson 2004b, Gatesy et al. 2009) have

uncertainty of approximately two folds. In addition,

we have obtained a result that 15.7 (m/s) running is

possible even in the framework of Hutchinson et al's

work. In this paper, we have studied on this issue

from a different angle, namely, based on a

calculation of mechanical power output. A

calculation of this quantity has never been done in

this research field. This methodology is superior

than Hutchinson et al.'s methodology. Because,

Hutchinson et al.'s methodology relied on static

calculation. There is no explicit relation of running

velocity with the other quantity in the theory. The

discussion of Froude number is employed for speed

evaluation, however, it is primitive, and known that

it may contain two folds error (Rainforth and

Manzella, 2007). There is no such uncertain

parameter in the calculation of mechanical power

output.

For the final evaluation for running ability only

the quantity of power per kilogram of muscle mass

is a parameter in the calculation. In addition, there

has been detailed studies on how much muscle mass

Tyrannosaurus has for hind limb. It tells that

Tyrannosaurus has 15~16 % muscle mass for one

hind limb. Then, comparatively accurate evaluation

can be achieved. Note that approximately two folds

error can be contained in our mechanical power

calculation because of uncertainty of the position of

the center of mass. Even considering this factor the

data of power output of extant animal allows fast

running motion of

Tyrannosaurus. The speed is 15.7

(m/s), which is faster than human. Then, we can

conclude that a possibility of fast running of

Tyrannosaurus can not be excluded.

Figure 11 summarizes the published data and the

present data of running speed and Froude number

Fr.

The original Hutchinson and Garcia's estimation,

which deny a possibility of fast running is for

v=20

(m/s) and Fr=16 with hip height h=2.5 (m). Our data

presented by this paper does not conflict with their

evaluation.

We show how it looks like if

Tyrannosaurus runs in

a speed of 15.7 (m/s) in Fig.12. Two poles are

located with distance of 31.4 m as shown in Fig.12.

A car ran between them with 2.0 seconds, which

leads a speed of 15.7 (m/s) (56.9 km/h, 35.4 mph).

This scene was filmed at first, and next 3D

reconstructed

Tyrannosaurus was synthesized in the

scene.

COULD TYRANNOSAURUS RUN FAST? - Mechanical Power Calculation for 15.7 m/s Tyrannosaurus Running

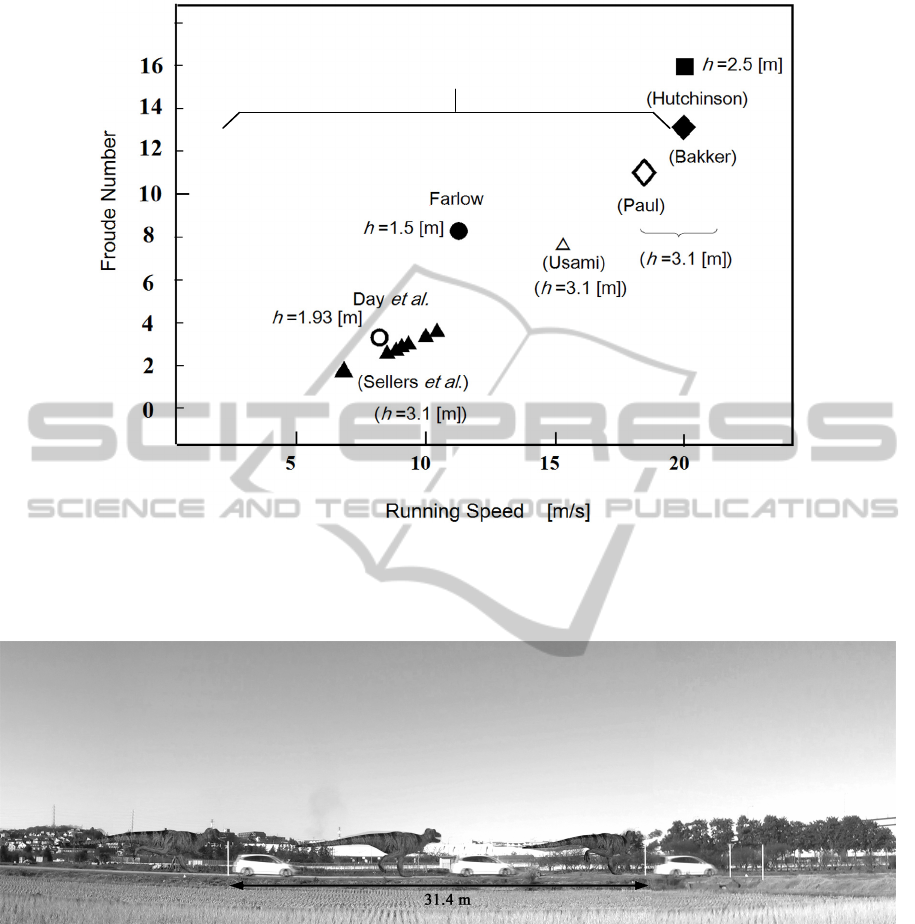
Figure 11: Running speed v.s. Froude number. Hutchinson and Garcia's data is located for v=20 (m/s) and Fr=16 with hip

height h=2.5 (m). They denied such fast running of Tyrannosaurus. However, the other data permit fast running of

Tyrannosaurus from the one that is comparable to human by Sellers et al. (Sellers et al. 2007) to the present result and Paul

and Bakker (Bakker 1986; Paul, 1988). The h represents hip height in the figure.

Figure 12: How it looks like if Tyrannosaurus runs in a speed of 15.7 (m/s) in the present world.

As it is noted in Section 3, searching the global

minimum of the evaluation function of running

velocity and vertical acceleration is a difficult

problem. Small difference of parameters changes

pattern of locomotion greatly as appeared in Fig.3

and Fig.4. We have carried out many running

simulations to obtain a good solution, i.e., the lowest

vertical acceleration and the fastest running speed.

Evolution algorithm is able to obtain a local

minimum of the evaluation function. However, it is

needed to obtain the global minimum of the

evaluation function, i.e., vertical acceleration and

running velocity for this problem. Then, developing

more sophisticated algorithm to bring an appropriate

solution easily is left as a future problem. If a better

algorithm was developed, it would be of great help

for the study of this research area.

ACKNOWLEDGEMENTS

The author thanks to Prof. Yoshiyuki Kazuyoshi to

provide human locomotion data using VICON

Running

No Running

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

system and his original software WaveEyes. The

author thanks to a referee who suggested power

output evaluation.

REFERENCES

Alexander, R. Mc. N.,1976. Estimates of speeds of

dinosaurs. Nature, vol. 261, p. 129-130.

Alexander, R. Mc. N., 1985. Mechanics of posture and gait

of some large dinosaurs, Zoological Journal of

Linnean Society, vol. 83, p. 1-25.

Alexander, R. Mc. N., 1989. The Dynamics of Dinosaurs

and Other Extinct Giants, Columbia University Press,

New York.

Alexander, R. Mc. N., 1996. Tyrannosaurus on the run,

Nature, vol. 379, p. 121-121.

Alexander, R. Mc. N., 2006. Dinosaur biomechanics,

Proceedings of the Royal Society, vol. B 273, p. 1849-

1855.

Alexander, R. Mc. N. and Jayes, A. S., 1983: A dynamic

similarity hypothesis for the gaits of quadrupedal

mammals, Journal of Zoology, vol. 201, p. 135-152.

Askew, G. N., March, R.L. and Ellington C, P., 2001a:

The mechanical power output of the flight muscles of

blue-breasted quail (Coturnix chinensis) during take-

off. Journal of Experimental Biology, vol. 204,

p.3601-3619.

Askew, G. N. and Marsh, R.L., 2001b: The mechanical

power output of the pectoralis muscle of blue-breated

quail (Coturnix chinensis): the in vivo length cycle and

its implications for muscle performance. Journal of

Experimental Biology, vol. 204, p. 3587-3600.

Bakker, R. T., 1986: Dinosaur Heresies. William Morrow,

New York.

Bates, K. T., Manning, P. L., Hodgetts, D. and Sellers, W.

I., 2009: Estimating Mass Properties of Dinosaurs

Using Laser Imaging and 3D Computer Modelling,

PLoS ONE, 4 (2): e4532 doi:10.1371/

journal.pone.0004532.

Day, J. J., Norman, D. B., Upchurch, P. and Powell, H. P.,

2002: Dinosaur locomotion from a new trackway,

Nature, vol. 415, p. 494-495.

Dial, K. P. and Biewener, A. A. 1993. Pectorialis muscle

force and power output during different modes of

flight in pigeons (Columba livia), Journal of

Experimental Biology 176: 31-54.

Farlow, J. O., 1981: Estimates of dinosaur speeds from a

new trackway site in Texas, Nature, vol. 294, p. 747-

748.

Fogel, D. B., 1995. Evolutionary Computation, Toward a

New Philosophy of Machine Intelligence, IEEE Press,

Piscataway, NJ.

Fraser, A., 1970: Computer Models in Genetics, McGraw-

Hill , Donald Burnell, New York.

Fraser, A. 1970. Computer Models in Genetics, McGraw-

Hill , Donald Burnell, New York, 192pp.

Gatesy, S. M., Baker, M. and Hutchinson, J. R., 2009.

Constraint-Based Exclusion of Limb Poses for

Reconstructing Theropod Dinosaur Locomotion,

Journal of vertebrate paleontology, Vol. 29. p. 535-

544. Gatesy, S. M. and Biewener, A. A. 1991. Bipedal

locomotion: effects of speed, size and limb posture in

birds and humans, Journal of Zoology, London 224:

127-147.

Goldberg, D. E., 1989: Genetic algorithms in search,

optimization and machine learning, Addison Wesley.

Gray, J. 1936. Studies in animal locomotion. VI. The

propulsive powers of the dolphin, Journal of

Experimental Biology 13:192-199.

Holland, J. H., 1975. Adaptation in natural and artificial

systems, University of Michigan Press.

Hutchinson, J. R., 2004a. Biomechanical modeling and

sensitivity analysis of bipedal running. I. Extant Taxa.

Journal of Morphology, vol. 262, p. 421-440.

Hutchinson, J. R., 2004b. Biomechanical modeling and

sensitivity analyis of bipedal running ability. II.

Extinct taxa, Journal of morphology, vol. 262, p. 441-

461.

Hutchinson, J. R. and Garcia, M., 2002: Tyrannosaurus

was not a fast runne, Nature, vol. 415, p. 1018-1021.

Hutchinson, J. R. Ng-Thow-Hing, V. and Anderson, F. C.,

2007: A 3D interactive method for estimating body

segmental parameters in animals: Application to the

turning and running performance of Tyrannosaurus

rex., Journal of theoretical biology., vol. 246, p. 660-

680.

James, R. S., Atringham, J. D. and Goldspink, D. F. 1995.

The mechanical properties of fast and slow skeletal

muscles of the mouse in relation to their locomotory

function, Journal of Experimental Biology 198: 491-

502.

James, R. S. and Wilson, R. S. 2008. Explosive Jumping:

Extreme Morphological and Physiological

Specializations of Australian Rocket Frogs (Litoria

nasuta), Physiological and Biochemical Zoology 81:

176-185.

Lännergren, J.,Lindblom, P. and Johansson, B. 1982.

Contractile properties of two varieties of twitch muscle

fibtres in Xenopus laevis. Acta Physiologica

Scandinavica. 114: 523-535.

Lappin, A. K., Monroy, J. A., Pilarski, J. Q., Zepnewski,

E. D., Pierotti, D. J. and Nishikawa, K. C. 2006.

Storage and recovery of elastic potential energy

powers ballistic prey capture in toads. Journal of

Experimental Biology 209: 2535-2553.

Marsh, R. L. and John-Alder, H. B. 1994. Jumping

performance of hylid frogs measured with high-speed

cine film. Journal of Experimental Biology 188: 131-

141.

McGowan, C. P., Baudinette, R. V., Usherwood, J. R. and

Biewener A. A. 2005. The mechanics of jumping

versus steady hopping in yellow-footed rock wallabies.

Journal of Experimental Biology 208: 2741-2751.

Paul, G. S., 1988: Predatory Dinosaurs of the World,

Simon & Schuster, New York

Pontzer, H., Allen, V. and Hutchinson, J. R., 2009

Biomechanics of Running Indicates Endohermy in

COULD TYRANNOSAURUS RUN FAST? - Mechanical Power Calculation for 15.7 m/s Tyrannosaurus Running

Bipedal Dinosaurs, PLoS ONE, 4 (11):e7783

doi:10.1371/journal.pone.0007783.

Rainforth, E. C. and Manzella, M., 2007: Estimating

speeds of dinosaurs from trackways: a re-evaluation of

assumptions. GANJ 24: Contributions to the

paleontology of New Jersey (II) (Ed. Rainforth E. C. ),

p. 41-48.

Russell, D. A. and Beland, P. 1976. Running Dinosaurs,

Nature 264: 486.

Sellers, W. I., Manning, P. L., 2007: Estimating dinosaur

maximum running speeds using evolutionary robotics,

Proceeding of the Royal Society., vol. B 274, p. 2711-

2716.

Thulborn, R. A., 1981: Estimated speed of a giant bipedal

dinosaur, Nature, vol. 292, p. 273-274.

Thulborn, R. A., 1989: The Gais of dinosaurs. In. Gillette,

D. D. and Lockley, M. G. eds., Dinosaur Tracks and

Traces, p. 39-50. Cambridge University Press,

Thullborn, R. A., 1990: Dinosaur Tracks, Chapman &

Hall, London.

Usami, Y., 2011a, Was Tyrannosaurus really not a fast

runner? Reports of faculty of engineering (in

Japanese), Kanagawa University, pp13-17.

Usami, Y., 2011b: On the possibility of fast running of

heavy theropod Tyrannosaurus. Submitted to

BIOPHYSICS.

Usami, Y., 2011c: How fast Tyrannosaurus could run ?

Submitted to BIOPHYSICS.

Usami, Y., et. al., 1998: Reconstruction of Extinct

Animals in the Computer. Reconstruction of Extinct

Animals in the Computer. In. Adami, C., Belew, R. K.,

Kitano, H. and Taylor C.E. eds., Artificial Life VI, p.

173-177. MIT Press, UCLA.

Wallace, R. L. and Brooks, W. S. 2003. A dinosaur

trackways exerceis, Bioscene, vol. 29, p. 3-7.

Weis-Fogh, T., Alexander, R. Mc. N. and Pedley, T. J.

1977. The sustained power output from striated

muscle. In, Pedley, T. ed., Scale Effects in Animal

Locomotion, p. 511-525. Academic Pres Inc., New

York.

Wilson, R. S., Franklin, C. E. and James, R. S. 2000.

Allometric scaling relationships of jumping

performance in the striped marsh frog Limnodynastes

peronii. Journal of Experimental Biology 203: 1937-

1946.

ERRATUM

"COULD TYRANNOSAURUS RUN FAST?

MECHANICAL POWER CALCULATION FOR 15.7 m/s

TYRANNOSAURUS RUNNING" by Y.Usami.

Numerics of the vertical left hand axis in Fig.8 and Fig.9

are 1~5 instead of 10~50. These are simple notation

mistakes. Fig.6 and Fig.7 yield to these results. And, it

matches Fig.10.

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications