MULTILAYER SPLINE-BASED FUZZY NEURAL NETWORK

WITH DETERMINISTIC INITIALIZATION

Vitaliy Kolodyazhniy

Department of Psychology, University of Salzburg, Hellbrunnerstrasse 34, 5020 Salzburg, Austria

Keywords: Multilayer perceptron, B-spline, Nonlinear synapse, Fuzzy rule, Deterministic initialization, Singular value

decomposition.

Abstract: A multilayer spline-based fuzzy neural network (MS-FNN) is proposed. It is based on the concept of

multilayer perceptron (MLP) with B-spline receptive field functions (Spline Net). In this paper, B-splines

are considered in the framework of fuzzy set theory as membership functions such that the entire network

can be represented in form of fuzzy rules. MS-FNN does not rely on tensor-product construction of basis

functions. Instead, it is constructed as a multilayered superposition of univariate synaptic functions and thus

avoids the curse of dimensionality similarly to MLP, yet with improved local properties. Additionally, a

fully deterministic initialization procedure based on principal component analysis is proposed for MS-FNN,

in contrast to the usual random initialization of multilayer networks. Excellent performance of MS-FNN

with one and two hidden layers, different activation functions, and B-splines of different orders is

demonstrated for time series prediction and classification problems.

1 INTRODUCTION

Multilayer perceptron (MLP) (Haykin, 1998) has

been perhaps the most popular neural network

architecture for more than two decades already due

to its universal approximation properties and ease of

practical implementation.

MLPs construct global approximations of

multivariate function data and are capable of

generalizing their response to regions of the input

space where little or no training data is present (Lane

et al., 1990). In such a way, MLP also avoids the

curse of dimensionality since the number of the

neurons of MLP depends only on the geometric

properties of the target function but not on the

dimension of the input space (Xiang et al., 2005;

Barron, 1992; Barron, 1993). However, the global

nature of the weight updating can be a disadvantage

for data with complex local structure. Furthermore,

the random initialization of MLP leads to quite

different results of training depending on the initial

weights, even with improved initialization

techniques (Nguyen and Widrow, 1990;

Lehtokangas et al., 1995; Erdogmus et al., 2005).

To add local properties to MLP approximations,

the Spline Net architecture was proposed (Lane et

al., 1990) in which the synaptic connections in form

of simple gains are replaced with nonlinear functions

constructed using B-splines. The authors of the

Spline Net presented the general concept of this

model and an example of a network with two layers,

linear B-splines, random initialization, and a

standard backpropagation algorithm.

In the present paper, we propose a generalized

model called ‘Multi-layer Spline-based Fuzzy

Neural Network’ (MS-FNN) with fully deterministic

initialization and more efficient training.

2 ARCHITECTURE

A Spline Net model (Lane et al., 1990) with

inputs,

layers, and

outputs can be defined as

⎥

⎦

⎤

⎢

⎣

⎡

∑

−

],1[],[][],[

)(

ilhl

lhl

ofo

(1)

where

nh ,,1 …= , Ll ,,1 …

, Dn ≡

, Pn

≡ ,

],[ hl

is the output of neuron h in layer l,

],[

≡

is the hth network output,

xo ≡

],0[

is the ith

network input,

]0,[

≡

o ,

][l

is the sigmoid

activation function for layer l,

n is the number of

475

Kolodyazhniy V..

MULTILAYER SPLINE-BASED FUZZY NEURAL NETWORK WITH DETERMINISTIC INITIALIZATION.

DOI: 10.5220/0003652604750481

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FCTA-2011), pages 475-481

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

neurons in layer l, and

],[ hl

f is the nonlinear

synaptic connection function of input i of the hth

neuron in layer l:

∑

−−

ill

ilhl

woof

],[

],1[][

],1[],[

)()(

(2)

In (2),

][

is the jth receptive field function of

input i of layer l,

],[

is its synaptic weight in

neuron h, and

m is the number of receptive field

functions for each input of layer l. All receptive field

functions of a layer are shared between all neurons

of that layer.

Taking into account (2), we can re-write (1)

using a more compact vector-matrix notation:

)]([

]1[][][][][ −

lllll

oμWσo

Ll ,,1 …=

(3)

In (3),

oo ),,(

],[

]1,[][

…=o

is the vector of

outputs of layer

l ,

][l

σ is a vector activation

function of vector argument,

][l

W is a matrix of

synaptic weights in layer

l sized )(

1 lll

mnn

−

× , and

…),(),([)(

]1,1[][

2,1

]1,1[][

1,1

]1[][ −−−

llllll

μμ

oμ

.)](,

],1[

][

−

…

A convenient choice for the receptive field

functions is B-splines due to their nice local

properties (Lane et al., 1990). To maintain a

partition of unity for any value of x, additional

marginal functions should be added at both ends of

the universe of discourse of x for splines of order>2

(see Fig.

1). As in (Lane et al., 1990, Bodyanskiy et

al., 2005, Kolodyazhniy, 2009, Kolodyazhniy et al.,

2007), we assume that the positions of knots of B-

splines are not optimized and are chosen

equidistantly.

B-splines in nonlinear synapses (2) can be

considered as membership functions of fuzzy sets

(Zhang, Knoll, 1998, Kolodyazhniy, 2009).

Therefore, the nonlinear synapses (2) can be

interpreted as elementary fuzzy inference systems

containing the following fuzzy rules:

.,,THEN

ISIF

],[

]1,[

][

],1[

wfwf

−

…

(4)

In (4),

][

O is a fuzzy label such as ‘LARGE’,

‘MEDIUM’, ‘SMALL’, etc. determined by the

respective membership function

][

. Note that the

B-spline membership functions of order>2 are not

normal, i.e. the maximum values of non-marginal

functions are below one (see Fig. 1), such that the

partition of unity is always preserved.

−0.5 0 0.5 1 1.5

0.5

Order=1

−0.5 0 0.5 1 1.5

0.5

Order=2

−0.5 0 0.5 1 1.5

0.5

Order=3

−0.5 0 0.5 1 1.5

0.5

Order=4

Figure 1: B-spline membership functions (MF) of order 1

to 4 defined for variable ]1,0[

∈

x such that 5 membership

function are defined over the universe of discourse of

Shaded areas correspond to the marginal B-functions.

Denoting the sum of synaptic outputs of neuron

h in layer l as

⎥

⎦

⎤

⎢

⎣

⎡

∑

−

],1[],[],[

)

(

ilhl

yfa

(5)

we can define the following activation functions that

will be subsequently used:

],[],[][

)(:Identity

hlhll

aa =

(6)

)]exp(1/[1)(:Sigmoid

],[],[][ hlhll

aa −+=

(7)

.)exp(/)exp(

)(:Softmax

],[],[

],[][

∑

iLhL

hLL

aσ

(8)

The original Spline Net model (Lane et al., 1990)

contained only sigmoid activation. A neuron with

linear B-splines (triangular membership functions)

and identity activation function coincides with the

neo-fuzzy neuron proposed in (Yamakawa et al.,

1992) and is used in (Bodyanskiy et al., 2005;

Kolodyazhniy et al., 2007) for constructing the two-

layered Neuro-Fuzzy Kolmogorov’s Network

(NFKN). Due to the generalization of the previously

developed NFKN model to multiple layers, we call

the neural net described in this paper ‘Multilayer

spline-based Fuzzy Neural Network’ (MS-FNN).

The architecture of MS-FNN (Fig. 2) is similar to

that of Spline Net except for the choice of activation

functions but the initialization and training

algorithms are different (see sections 3 and 4).

In case of two layers and the identity activation

functions, the MS-FNN architecture coincides with

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

476

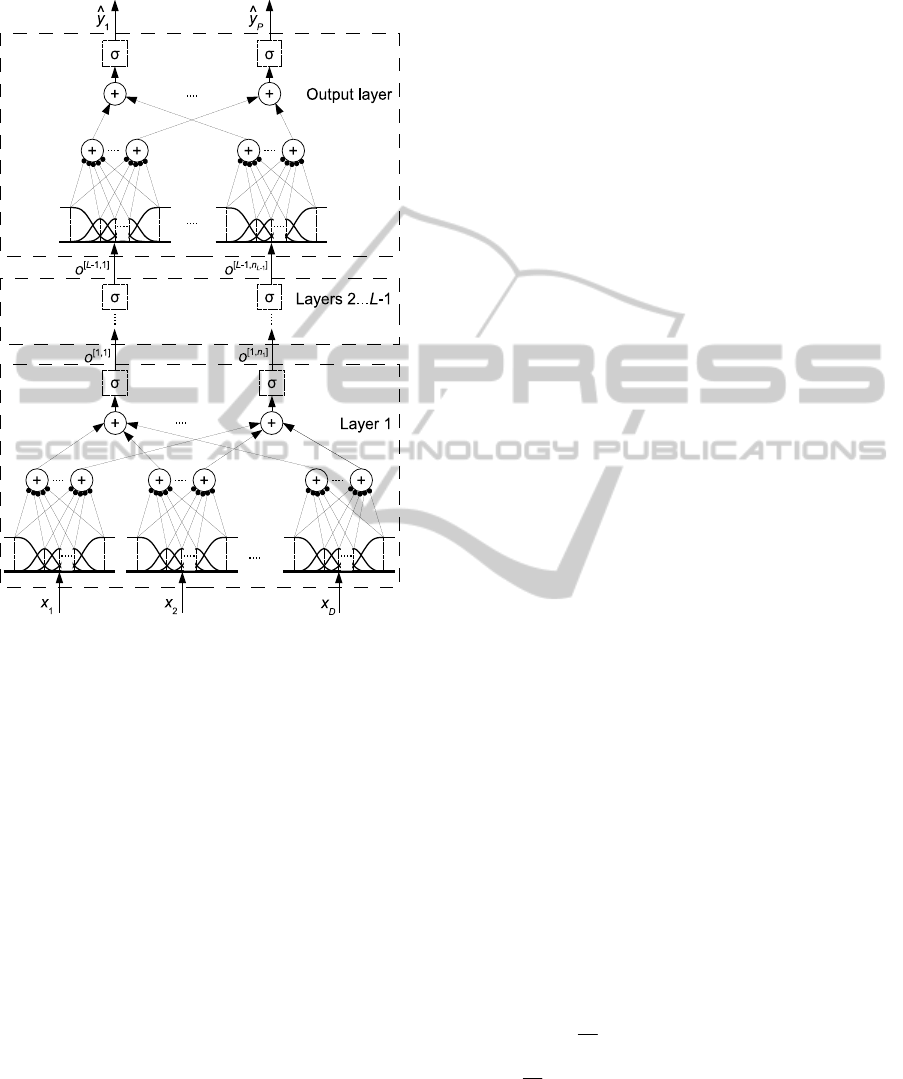
the Neuro-Fuzzy Kolmogorov’s Network (NFKN)

(Bodyanskiy et al., 2005; Kolodyazhniy, 2009).

Figure 2: MS-FNN architecture with

layers: dots (

•

)

represent synaptic weights, sigmoids (

) are optional.

In contrast to MLP or Spline Net, the hidden

layers of MS-FNN may not contain sigmoid

activation functions at all because the required

nonlinear transformations can be performed by

nonlinear synapses. The sigmoid function should be

included in the output layer for binary classification

with the

cross-entropy error function.

For multinomial classification with cross-

entropy, the

softmax activation function in the output

layer is used (Bishop, 1995). The use of the sigmoid

in hidden layers is optional and should be decided

based on performance in a particular problem.

The MS-FNN model has a different structure

from the known B-spline-based neural networks (see

e.g. Coelho, Pessôa, 2009, Wang, Lei, 2001, Cheng

et al., 2001) and fuzzy systems (Zhang and Knoll,

1998) that are constructed of multidimensional basis

functions being

tensor products of univariate B-

splines. This approach is plagued by the

curse of

dimensionality

: the number of basis functions and

associated weights grows

exponentially with

increase of the input space dimension.

In contrast, MS-FNN relies on multilayer

superposition of univariate synaptic functions

constructed using B-splines thus avoiding the curse

of dimensionality similarly to MLP.

3 DETERMINISTIC

INITIALIZATION

Let us assume that the number of neurons in a layer

in MS-FNN does not exceed the total number of

membership functions in that layer, i.e.

lll

mnn ⋅≤

−1

(9)

This assumption is adequate for quite a wide

range of problems. It implies that the number of

neurons in a layer

l can be between one and

mn ⋅

−1

where

1−l

n is the number of inputs of layer l and

Dn ≡

. For instance, in a network with ten inputs

and four membership functions per input the

maximum number of neurons in the first hidden

layer will be forty, which is sufficient in most cases.

Based on (9), the initialization of hidden layer

weights in MS-FNN can be performed

deterministically via linear PCA as proposed in

(Kolodyazhniy et al., 2007; Kolodyazhniy, 2009) for

the hidden layer of NFKN, such that all neurons in a

layer are initialized with mutually orthogonal weight

vectors. Here we generalize this approach to more

than one hidden layer.

Given a training data set containing

N patterns,

the PCA procedure is applied to the matrices of

membership degrees

[

]

lllll

N))((,)),1((

]1[][]1[][][ −−

= oμoμM … for all

hidden layers

1,,1

−

Ll …

successively, starting

from the first hidden layer with

xx ),,(

]0[

…== xo

. The vector of weights of the

hth hidden neuron in layer l corresponding to the hth

row of matrix

][l

W in (3) is assigned the transposed

hth loading (transposed hth column) from the matrix

found as a result of singular value decomposition

VΣUM =

][

(10)

where

][l

is equal to

][l

with mean values

subtracted column-wise.

After the

lth layer has been initialized, the input

data is propagated through layer

l, and the matrix of

membership degrees

]1[ +l

is computed followed

MULTILAYER SPLINE-BASED FUZZY NEURAL NETWORK WITH DETERMINISTIC INITIALIZATION

477

by weight initialization for layer

1+l using PCA as

described above. The output layer weights are

initialized with zeros.

If there is

only one neuron in a layer, its initial

weights for each nonlinear synapse (2) can be

chosen as linearly increasing, e.g. from zero to one.

During initialization of MS-FNN the

knots of B-

spline functions in the first hidden layer are set such

that the centers of the leftmost and the rightmost

non-marginal B-splines are assigned the minimum

and the maximum values of the corresponding

network input. The centers of B-splines between the

leftmost and the rightmost non-marginal functions

are distributed equally between them. The centers of

the marginal functions are set to the left and to the

right of the leftmost and the rightmost nonmarginal

functions, respectively, at the same distance as

between all the non-marginal functions.

If a

further hidden layer 1−l has sigmoidal

activation, then the centers of the non-marginal

membership functions of layer

l are distributed

equidistantly in the interval of

]1,0[

. Otherwise, the

minimum and maximum output values of all neurons

in layer

1−l

are computed and used for setting the

centers of membership functions in layers

l in the

same way as in the first layer. In such a way,

undesired saturations leading to neuron

underutilization and network paralysis during

training are avoided and the training is accelerated.

In case of sigmoid activation functions in layer

−

l ,

the knots of layer l should be positioned only once

during initialization such that the centers of the non-

marginal functions are distributed equidistantly in

the interval [0,1]. No knot re-positioning in layer l

during training is required because the preceding

neuron outputs are always in [0,1].

The entire initialization procedure is performed

layer by layer starting from the first hidden layer.

4 TRAINING

For regression, the error function is sum of squared

errors, and cross-entropy for classification.

For the both error functions described above, we

use resilient propagation (RPROP) which is a very

fast learning scheme (Riedmiller and Braun, 1993).

The weight update rule is without weight

backtracking (Rprop

–

, see Igel, C., Hüsken, M.,

2003) with the following parameters for MS-FNN:

5.0=

−

2.1=

6min

−

=Δ , 1.0

max

=Δ ,

1.0

=Δ .

To speed up batch training, the values of

membership functions in the first hidden layer of

MS-FNN are computed only once and then stored

throughout training because they do not change.

For layer l with identity activation in the

preceding layer 1

−

l , the B-spline knots are re-

positioned after each weight update with the RPROP

algorithm as in the initialization phase. This is done

to avoid saturations in synapses of the layer l,

because the outputs of layer

1−l are not limited to

the range of

]1,0[ in absence of a sigmoid activation

function. This knot re-positioning leads to a gradual

‘inflation’ of the distances between spline knots in

layer l following an approximately linear trend.

After training, the spline knots in each layer with

preceding identity activation can be re-set to their

initial positions with centers of non-marginal

functions between

]1,0[ , and the synaptic weights in

the preceding layer can be re-scaled to map the

respective neuron outputs onto

]1,0[ without

affecting the overall input-output mapping of the

MS-FNN model (Wang et al., 2009).

5 EXPERIMENTS

The MS-FNN model and the RPROP algorithm were

implemented in MATLAB v. 6.5 under Windows

XP on a PC with 2 GB of RAM and an Intel Core

Duo T2500 CPU with a 2.0 GHz clock. For

comparison, an MLP was implemented using the

MATLAB Neural Networks Toolbox with

modifications by the author for classification

problems which included the cross-entropy error

function. The MLP contained the hyperbolic tangent

activation function in hidden layers designated

below as ‘tanh’ in contrast to the ‘sigmoid’ (7) and

was trained with the same RPROP algorithm except

for two parameters:

max

=Δ and 07.0

(standard values of the MATLAB Toolbox).

The PCA initialization technique was used for

MS-FNN (except for the N-parity problem where

linear initialization was used, see section 3), while

the MLP was initialized randomly via the Nguyen-

Widrow algorithm (Nguyen and Widrow, 1990).

We report the best results and the training time,

although the latter might be biased in favor of the

MLP model because of the extensive code

optimization in the MATLAB Neural Network

Toolbox. It is expected that the training time for

MS-FNN can also be reduced via code optimization.

For MLP, the input data were standardized by

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

478

subtracting the mean value of the respective input

and dividing by its standard deviation which in all

cases resulted in a better performance of the MLP

compared to scaling onto the hypercube

]1,1[− . For

MS-FNN, the data were not transformed because the

membership functions of the input layer always

scale the data onto the unit hypercube.

5.1 Time SeriesPrediction

We compared the performance of MS-FNN and

MLP models in the forecasting of the well-known

Mackey-Glass (MG) time series (Mackey and Glass,

1977) for

17=

. The error function was sum of

squared errors. The task was to predict the value of

the time series

)85( +tx using values

)(tx

, )6( −tx ,

)12( −tx , and )18( −tx as inputs for

3117...118=t

for training and

4117...3118=t

for testing.

First, an MS-FNN model with 2 hidden layers

with 10 neurons in each and one output neuron was

created and trained for 4000 epochs. For network

configuration and achieved prediction accuracy see

Table 1, where ‘W’ is the number of weights, ‘n’

and ‘m’ represent the number of neurons and

membership functions in the respective layers, and

‘Hid.Act’ and ‘Out.Act.’ stand for the activation

functions in the hidden and output layers,

respectively.

Then an MLP with two hidden layers with 30

neurons in each and one output neuron with a

number of parameters approximately equal to that of

MS-FNN was trained ten times for 10000 epochs

which took approximately the same time as the

training of MS-FNN. In Table 1 the best result out of

the ten runs is given (NRMSE Test=0.019) and is by

ca. 28% worse than that of MS-FNN (NRMSE

Test=0.0148).

5.2 Classification

For classification problems, all neural networks were

trained using the cross-entropy error functions. A

description of the data used for classification can be

found in Table 2. The target class variables had

values of 0 or 1 for both MS-FNN and MLP.

The N-Parity problem was solved for

20...2

with MS-FNN and for

13...2=N

with MLP. The

MS-FNN classifier contained two layers, each with

one neuron. In the hidden layer neuron all

membership functions were of first order, and of

second order in the output neuron. The number of

membership functions in the first layer neuron was

two per input, and

1+N

in the output neuron. With

this configuration, the network was able to solve the

N-parity problem without errors after only seven

epoch of training for any N between 2 and 20 (see

Table 3). Apparently, the scaling behavior of MS-

FNN would be the same also in higher dimensions.

For comparison, the N-parity problem was

solved for

13...2

using MLP with one hidden

layer containing N neurons which is the minimum

required for an MLP to converge in this problem

(Rummelhart and McClelland, 1986). The MLP was

trained for 1000 epochs. If no classification errors

were reached earlier, the training was stopped. For

each N, there were 10 runs, each with a different

random initialization. The results of the 10 runs were

averaged (see Table 4). For each N between 2 and

13, in at least 2 runs the training converged with no

classification errors. For

13=N

, the MLP’s shortest

training time (61.8s) was greater than that for MS-

FNN for

while the training set contained

128 times fewer patterns (8192 instead of 1048576)

and the number of inputs was 13 instead of 20.

To the author’s knowledge, this result for MS-

FNN is one of the very best reported so far in the

neural network community for the N-parity problem

in the dimension of the solved problem, network

size, and training time for a general-purpose neural

network, including (Wilamowski and Yu, 2010)

where N=16 was solved with a 9% success rate with

a fully connected MLP.

In the two spirals problem, the task was to find

the smallest network capable of classifying points

belonging to one of two intertwined spirals without

errors. Each of the two spirals had 97 points

(Wieland, 1988). For MS-FNN, exhaustive search

was performed for networks with one hidden layer

with one to eight neurons and

11...4

=m and

17...5

=m until a network able to classify the two

spirals without errors after up to 1000 epochs of

training was found. The search was done for linear,

quadratic, and cubic B-splines. As can be seen from

Table 3, the smallest MS-FNN had only two hidden

layer neurons with sigmoid activation, quadratic

splines in their synapses, and reached zero

classification errors after 384 epochs of training.

For MLP, a search for the smallest architecture

capable of classifying the two spirals without errors

was done for architectures with two hidden layers

each containing n neurons for

10...6=n

and 100

runs of up to 10000 epochs of training for each n. As

can be seen from Tables 3 and 4, the MS-FNN

model had approximately three times fewer

parameters (48 vs. 151) and converged much faster

than MLP.

MULTILAYER SPLINE-BASED FUZZY NEURAL NETWORK WITH DETERMINISTIC INITIALIZATION

479

For the same data with 194 points training with

RPROP 1500 to 15000 epochs were reported for a

four-layered perceptron-like network with additional

shortcut connections (Riedmiller and Braun, 1993).

The UCI Letter data set (see UCI) is a larger-

sized multinomial classification problem. The MS-

FNN model providing the highest classification

accuracy had one hidden layer with identity

activation and 38 neurons, and 26 neurons in the

output layer. The search was done among

architectures with one hidden layer with 16 to 40

neurons with cubic splines in their synapses with

and without sigmoid activation in the hidden layer.

For comparison, MLPs with two hidden layers

containing 70, 80, 90, and 100 neurons in each of the

hidden layers were tested 10 times for each

configuration with different random initializations.

Both the MS-FNN and MLP models were trained for

500 epochs. The training was stopped earlier if all

patterns in the training set were classified correctly.

As can be seen from Tables 3 and 4, the MS-FNN

model provided a slightly lower error for the test

data (4.1% vs. 4.225%) with fewer weitghts. Both of

these results rank among the very best achieved for a

single neural network. E.g., in (Schwenk and

Bengio, 2000) a testing error of 6.1% is reported for

a single MLP on the same dataset, and for ensembles

it was 4.3% for bagging and 1.5% for boosting, the

latter being the best result known to the author.

6 Conclusions

A practical implementation of a multilayer spline-

based fuzzy neural network (MS-FNN) with

improved local properties and deterministic

initialization was presented and improved

performance of the proposed model was

demonstrated in comparison with a conventional

multilayer perceptron.

The deterministic initialization of the MS-FNN

model, among other advantages, makes a direct

structure optimization of the neural network

possible, even using a straightforward exhaustive

search approach, because the number of parameters

determining the structure (the number of neurons

and membership functions) is small and the possible

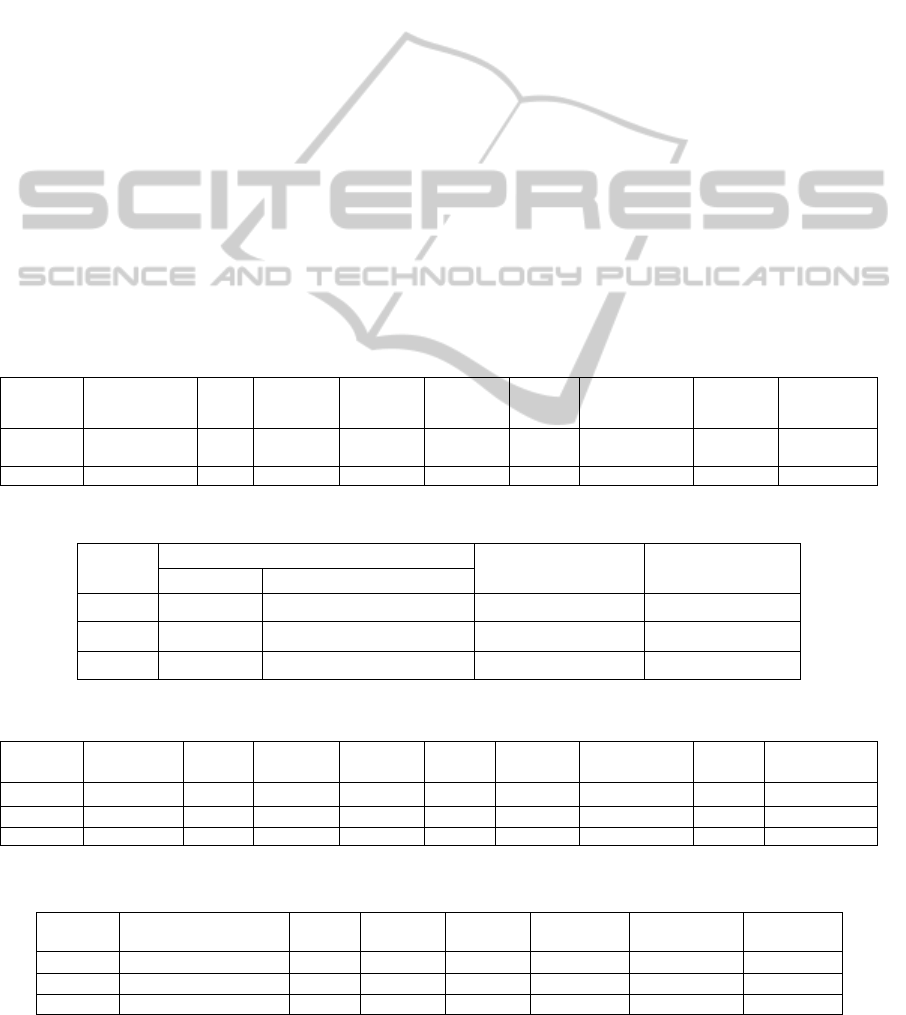
Table 1: Results of prediction of the Mackey-Glass time series 85 steps ahead.

Model

NRMSE Train,

Test

W Hid. act. Out. act. n m Spline order Epochs

Training

time, s

MS-FNN

0.0142,

0.0148

1090 sigmoid identity 10, 10, 1 7, 7, 11 4, 4, 4 4000 910.2

MLP 0.0181, 0.019 1111 tanh identity 30, 30, 1 – – 10000 902.6

Table 2: Datasets used for classification.

Dataset

Number of patterns

Number of attributes Number of classes

Training Testing

N-parity 4...1048576 – 2...20 2

Spirals 194 – 2 2

Letter 16000 4000 16 26

Table 3: Classification results with MS-FNN. For N-parity, results for

20...2

are shown.

Dataset

Error, %

Train, Test

W Hid. act. Out. act. n m Spline order Epochs

Training time,

N-parity 0, – 7...61 identity sigmoid 1, 1 2, 3...21 1, 2 7 0.16...44.4

Spirals 0, – 48 sigmoid sigmoid 2, 1 4, 16 3, 3 384 7.07

Letter 0.13, 4.1 12540 identity softmax 38, 26 6, 9 4, 4 500 2123.3

Table 4: Classification results with MLP. For N-parity, results are average of 10 runs for

13...2=N

Dataset Error, % Train, Test W Hid. act. Out. act. n Epochs

Training

time, s

N-parity 0.078...12.5, – 9...196 tanh sigmoid 2...13, 1 148.9...941.2 0.5...61.8

Spirals 0, – 151 tanh sigmoid 10, 10, 1 5743 28.4

Letter 0, 4.225 14426 tanh softmax 100, 100, 1 303 792.5

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

480

values of these parameters are natural numbers with

quite a limited range. For a particular combination of

these parameters the mapping realized by the neural

network is deterministic for the given training

algorithm and the number of training epochs.

Future research of the author would include the

development of more efficient algorithms for

structure optimization, as well as the improvement

of interpretability of fuzzy rules for knowledge

extraction from the trained net.

REFERENCES

Haykin, S., 1998. Neural Networks: A Comprehensive

Foundation, Prentice Hall, Upper Saddle River, 2nd

edition.

Lane S. H., Flax, M. G., Handelman, D. A., Gelfand, J. J.,

1990. Multi-Layer Perceptrons with B-Spline Rece-

ptive Field Functions. In Advances in Neural

Information Processing Systems, R. P. Lippman, J.

Moody, D. S. Touretzky (Eds.), Vol. 3,. Morgan

Kaufman, San Francisco, pp. 684-692.

Xiang, C., Ding, S. Q., Lee, T.H., 2005. Geometrical In-

terpretation and Architecture Selection of MLP. IEEE

Transactions on Neural Networks, 16, 84-96.

Barron, A. R., 1992. Neural Net Approximation, In Pro-

ceedings of the 7th Yale Workshop Adaptive and

Learning Systems, New Haven, CT, 1992, pp. 69–72.

Barron, A. R., 1993. Universal Approximation Bounds for

Superpositions of a Sigmoidal Function. IEEE Tran-

sactions on Information Theory, 39, 930–945.

Nguyen, D., Widrow, B., 1990. Improving the Learning

Speed of 2-layer Neural Networks by Choosing Initial

Values of the Adaptive Weights. In Proceedings of the

International Joint Conference on Neural Networks,

vol. 3, 1990, pp. 21–26.

Lehtokangas, M., Saarinen, J., Kaski, K., Huuhtanen, P.,

1995. Initializing Weights of a Multilayer Perceptron

Network by Using the Orthogonal Least Squares

Algorithm. Neural Computation, 7, 982-999.

Erdogmus, D., Fontenla-Romero, O., Principe, J. C.,

Alonso-Betanzos, A., Castillo, E., 2005. Linear-Least-

Squares Initialization of Multilayer Perceptrons

Through Backpropagation of the Desired Response.

IEEE Transactions on Neural Networks, 16, 325-337.

Bodyanskiy, Ye., Gorshkov, Ye., Kolodyazhniy, V.,

Poyedyntseva, V., 2005. Neuro-fuzzy Kolmogorov’s

Network, Lecture Notes in Computer Science, W.

Duch et al. (Eds.), Vol. 3697, Springer, Berlin,

Heidelberg, New York, pp. 1-6.

Kolodyazhniy, V., 2009. Spline-based Neuro-fuzzy

Kolmogorov’s Network for Time Series Prediction. In

Proceedings of the 17th European Symposium on

Artificial Neural Networks (ESANN 2009), Bruges,

Belgium, 2009, pp. 153-158.

Kolodyazhniy, V., Klawonn, F., Tschumitschew, K., 2007.

A Neuro-fuzzy Model for Dimensionality Reduction

and its Application. International Journal of

Uncertainty, Fuzziness, and Knowledge-Based

Systems, 15, 571-593.

Zhang, J., Knoll, A., 1998. Constructing Fuzzy Controllers

with B-Spline Models — Principles and Applications.

International Journal of Intelligent Systems, 13, 257-

285.

Yamakawa, T., Uchino, E., Miki, T., Kusanagi, H., 1992.

A Neo Fuzzy Neuron and its Applications to System

Identification and Prediction of the System Behavior,

In Proceedings of the 2nd International Conference on

Fuzzy Logic and Neural Networks (IIZUKA-92),

Iizuka, Japan, 1992, pp. 477-483.

Bishop, C. M., 1995. Neural Networks for Pattern

Recognition, Clarendon Press, Oxford.

Coelho, L. d. S., Pessôa, M. W., 2009. Nonlinear

Identification Using a B-Spline Neural Network and

Chaotic Immune Approaches. Mechanical Systems

and Signal Processing, 23, 2418-2434.

Wang, K., Lei, B., 2001. Using B-spline Neural Network

to Extract Fuzzy Rules for a Centrifugal Pump

Monitoring. Journal of Intelligent Manufacturing, 12,

pp. 5-11.

Cheng, K. W. E., Wang, H. Y., Sutanto, D., 2001.

Adaptive Directive Neural Network Control for Three-

Phase AC/DC PWM Converter, Proc. Inst. Electr.

Eng.—Elect. Power Appl., vol. 148, no. 5, pp. 425–

430.

Riedmiller, M., Braun, H., 1993. A Direct Adaptive

Method for Faster Backpropagation Learning: The

Rprop Algorithm. Proceedings of the IEEE

International Conference on Neural Networks, 1993,

pp. 586-591.

Igel, C., Hüsken, M., 2003. Empirical Evaluation of the

Improved Rprop Learning Algorithms.

Neurocomputing, 50, 105-123.

Wang, D., Zeng, X.-J., Keane, J. A., 2009. Intermediate

Variable Normalization for Gradient Descent Learning

for Hierarchical Fuzzy System. IEEE Transactions on

Neural Networks, 17, 468-476.

Mackey, M. C., Glass, L., 1977. Oscillation and Chaos in

Physiological Control Systems. Science, 197, 287-289.

Rumelhart, D. E., McClelland, J. L., 1986. Parallel

Distributed Processing vol. 1, Cambridge, MIT press.

Wilamowski, B.M., Yu H., 2010. Improved Computation

for Levenberg–Marquardt Training. IEEE

Transactions on Neural Networks, 21, 930-937.

Wieland, A., 1988. Two spirals.

http://www.boltz.cs.cmu.edu/benchmarks/two-

spirals.html. CMU Repository of Neural Network

Benchmarks.

UCI Machine Learning Repository. http://archive.ics.uci.

edu/ml/index.html

Schwenk, H., Bengio, Y., 2000. Boosting Neural

Networks. Neural Computation, 12, 1869–1887.

MULTILAYER SPLINE-BASED FUZZY NEURAL NETWORK WITH DETERMINISTIC INITIALIZATION

481