SPATIAL-BASED FUZZY CLASSIFICATION OF LAND

SUITABILITY INDEX FOR AGRICULTURE DEVELOPMENT

A Model Validation Perspective

Sumbangan Baja, Andi Ramlan

Department of Soil Science, Hasanuddin University, Makassar, Indonesia

Muhammad Ramli

Stalitan Maros, Ministry of Agriculture, Jakarta, Republic of Indonesia

Keywords: Fuzzy set, Land suitability index, Spatial modeling, Corn development.

Abstract: The primary aim of this research is to develop and test fuzzy modeling procedures to assess spatial

distribution of actual corn yields in the field in relation to land characteristics. This experiment implements

a fuzzy set methodology to generate a land suitability index (LSI) for corn development. It also uses a direct

yield record method in the fields, and utilizes geographic information systems (GIS) in spatial analysis, in

synchrony with global positioning system (GPS). This study produced a set of spatial information on LSI on

a cell-by-cell basis in the study area. A simple regression method was also employed to calculate spatial

correlation between two sets of information (i.e., corn yield in kg/ha and fuzzy set-based LSI). Although the

correlation coefficient (R

) is relatively low, the scatter points have shown a good indication that the higher

the LSI the better yield can be produced in the area under consideration. Spatial interpolation was then

undertaken to map predicted corn yields on a regional basis. Spatial segmentation of land area in form of a

fuzzy-based land suitability index map can assist land managers or decision makers in allocating future corn

cultivation area in the study region.

1 INTRODUCTION

Basically, there are at least three main reasons for

using fuzzy set methodology rather than a Boolean

technique in land suitability evaluation. First, in the

Boolean classification technique an ordinary set

defines an exact boundary, while a fuzzy set permits

flexibility in defining the boundary of the object in

the set. Second, only two possibilities exist in the

Boolean technique: an element or suitability level is

either included or excluded in a set, while in the

fuzzy set the degree of closeness to the ideal point is

considered in the inclusion. Finally, unlike the fuzzy

set technique, Boolean logic cannot take account of

partial membership of an element in a set. Therefore,

when using a raster GIS, calculation can be made on

a cell-by-cell basis (Baja et al., 2007; Maeda et al.,

2009), and this provides an opportunity for applying

statistical procedures (Olano et al., 1998).

However, limited number of model-based studies

on land suitability gives a comprehensive validation

exercise that could describe uncertainty (Cook and

Bramley, 2001). It is thus always necessary,

particularly in complex GIS modeling, that the

model built be tested for its validity. Commonly-

used approaches of model validation include testing

for predictive ability and comparison against

performance standards (Harrison, 1991). For land

suitability assessment, the second method may be

more appropriate to use, and land productivity

measures (such as crop yields, costs required for

improving biophysical constraints, etc.) are

employed as a performance standard.

From the perspective of fuzzy set-based

agricultural applications, a cell-by-cell land

suitability grade may be related to the actual

production in the field, while collection of yield

information over space and time has sometimes

outperformed our ability to interpret and apply the

data. There is therefore a need for a spatial based

model for generating information that can depict

stronger linkages between information sets on land

435

Baja S., Ramlan A. and Ramli M..

SPATIAL-BASED FUZZY CLASSIFICATION OF LAND SUITABILITY INDEX FOR AGRICULTURE DEVELOPMENT - A Model Validation Perspective.

DOI: 10.5220/0003653604350440

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FCTA-2011), pages 435-440

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

characteristics and crop yields on specified farmland

management in a given study region. The primary

aim of this study is to implement available fuzzy

modeling approaches in a spatial context, and to

assess and map the spatial distribution of corn (Zea

mays L.) yields in the field in relation to land

suitability indices. Geographic information Systems

(GIS) technology, was employed in synchrony with

global positioning system (GPS).

2 METODOLOGY

2.1 Study Area

The area selected for this study includes some parts

of the lower Jeneberang River catchment covering

an area of approximately 37.000 ha, located about

30 km Southeast of Makassar City, South Sulawesi,

Indonesia (Figure 1). According to existing land use

map, agriculture is the predominant land use in the

study region consisting of paddy field 16,725 ha

(45%), followed by shrubs 9,335 ha (25%), mixed

farms 5,071 ha (14%), forest 4,087 ha (11%), water

body (Bili-Bili Dam) 1,766 ha (5%), and residential

379 ha (1%). It was found in the study area that in

addition to rice, rainfed paddy field is also cultivated

with corn.

Figure 1: Location of study area.

2.2 Identification of Land under Corn

Cultivation

Identification of land under traditional corn

cultivation in the study area was undertaken during

cultivation period (March to April 2009). As many

of 31 farmers of corn cultivars from different

villages were involved in this study. These farms

were taken from different land units and identified

as having different land characteristics. At the same

time, soil samples with precise GPS records were

taken from different units for laboratory analysis. An

informal agreement was made between our

surveyors with these farmers to harvest the crops

together (in May and June), in order the corn yields

can be further weighted in kg/ha.

2.3 Calculating Land Suitability

Indices

A fuzzy set is most commonly used for

classifications of objects or phenomena in

continuous values, where the classes do not have

sharply defined boundaries. It deals with a class with

a continuum of grades of memberships (Zadeh,

1965). A fuzzy set A may be defined as follows:

A = {x, 

(x)} x  X

(1)

Where X = {x} is a finite set (or space) of objects or

phenomena, 

(x) is a membership function of X for

subset A.

Therefore, a fuzzy subset is defined by the

membership function (MF) that defines the

membership grades of fuzzy objects or phenomena

in the ordered pairs, consisting of the objects and

their membership grades. The MF of a fuzzy subset

determines the degree of membership of x in A

(Burrough et al., 1992).

Calculation procedure implemented in this study

utilizes an a priori membership function (MF) for

individual variables under consideration, where the

technique is called “a Semantic Import” (SI) model

(Burrough and McDonnel, 1998). Examples can be

seen in Baja et al. (2002a) and Davidson et al.

(1994). With this approach, the attribute values

considered are converted to common membership

grades (from 0 to 1.0), according to the class limits

specified by the analysts based on experience or

conventionally imposed definitions.

If MF(x

) represents individual MF values for i

land property x, then, the basic SI model function

take the following form in the computation process:

}]/)[(1{

)(

dbx

xMF





(2)

In the computation, it is crucial to examine an

appropriate fuzzy model parameter to suit each

decision criterion. The choice depends on the ‘trend

of performance’ of the respective land attribute in

accommodating a favorable condition for a selected

land use type (Baja et al., 2002b). Model parameters

include LCP (lower crossover point), b (central

concept), UCP (upper crossover point), and d (width

of transition zone).

Land and climate characteristics used for

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

436

calculating LSI in this experiment include drainage,

texture, soil depth, cation exchange capacity (CEC),

organic matter (OM), pH, slope, and average annual

rainfall (Appendix 1).

Based on its nature of data representation, land

characteristic information can be divided into

ordinal and cardinal numbers. The former include

site drainage, soil texture and structure, CEC, OM,

while the latter are pH, slope, and rainfall. The

individual MF value is calculated based on Equation

(2). For ordinal value, the technique used following,

for example, Figure 2, while for cardinal number it

implements Figure 3. These apply for the rest of

land characteristics.

Figure 2: Example for calculating MF values for ordinal-

based land characteristics.

Figure 3: Example for calculating MF values for cardinal-

based land characteristics.

As there are n land characteristics to be rated, the

MF values of individual land characteristics under

consideration are then combined using a convex

combination function to produce a join membership

function (JMF) of all attributes, Y as follows:

)()(





xMFYJMF



(3)

where 

is a weighting factor (see Table 1) for the

land property x, and MF(x

) denotes a membership

grade for the i

land property x.

Calculation of LSI was done on a cell-by-cell

basis, in a raster GIS data base. The result of such a

procedure is a map representing spatial distribution

of land suitability index in a continuous grade,

ranging from 0 (not suitable) to 1.0 (very suitable).

Table 1: Weighting factor for land characteristic used.

Land characteristics Weight, 

Site drainage 0.10

Soil texture and structure* 0.20

Solum depth 0.15

Cation exchange capacity, CEC (topsoil) 0.10

Organic matter, OM (topsoil) 0.05

pH (1:5 soil:water) 0.05

Slope gradient (%) 0.15

Rainfall (mm/annum) 0.15

2.4 Calculation of Corn Yields

Corn was harvested in a randomly determined land

sample of 2.5 by 2.5 sq metres, with 3 replications.

The harvested seeds of corn were then drayed at

approximately 14% water content. The drayed corn

seeds were then weighed and transformed in kg/ha,

using the following formula:

Wc-ha = 1,600 x Wc-spl (4)

Where Wc-ha is a weight of corn seeds in kg per ha,

Wc-spl is weight of corn seeds in each sample of 2.5

by 2.5 sq meters, and a coefficient of 1,600 is taken

from 10.000/(2.5 x 2.5).

2.5 Analysis of Correlation

Analysis of correlation was undertaken between land

suitability, LSI and corn yields in the study area

using a simple regression method. Land

characteristics and LSI were generated from the

results of laboratory test and GIS analyses, while

corn yield data were derived from the average seed

weight (from 3 replications).

2.6 Yield Mapping

Yield mapping was done using GPS and GIS, using

the formula generated from the analysis of

correlation. This map indicates spatial distribution of

corn yield in the study area under land management

currently practiced by farmers.

3 RESULTS AND DISCUSSION

3.1 Land Suitability Indices

Spatial distribution of land suitability index in a

continuous grade is depicted in Figure 4, and that for

grid values (i.e., LSI) in the data space can be seen

in Figure 5. It can be seen that use of fuzzy measures

SPATIAL-BASED FUZZY CLASSIFICATION OF LAND SUITABILITY INDEX FOR AGRICULTURE

DEVELOPMENT - A Model Validation Perspective

437

in a raster GIS can produce a detailed index of land

suitability; where in this application the values

ranges from around 0.30 (less suitable) to 1.0 (very

suitable) for corn development. It seems that the

most suitable areas for corn development is found in

the western section of study area. Based on the pixel

values trace from the criteria developed, it was

found that the main limitation for land units in the

east is topography, where slope is more than 15%.

Figure 4: Spatial distribution of LSI in the study area.

Figure 5: Distribution of LSI in the grid data space.

3.2 Spatial Distribution of Crop Yields

The result of field study was presented in form of

corn yields from different map units with clear

indication of ground coordinates and 31 village

names. It was found that yield variation occurs over

the study area, ranging from 500 kg/ha to 5.575

kg/ha. Identification from field study reveals that

agricultural land management were slightly different

from one farm land to another, which may contribute

to slight differences in a crop yield.

3.3 Correlation between LSI and

Yields

Correlation was tested between LSI and corn yields,

and the result can be seen in Figure 6, forming the

following formula:

Y = 5190X - 2020; R

= 0.61 (5)

Where Y is corn yield and X is average LSI of

corresponding land units in the study area.

Figure 6: Correlation between LSI and corn yield.

Although the coefficient of correlation (R

) is

relatively low, the scatter points have shown a good

indication that the higher the LSI the better yield can

be produced in the area under consideration. It is

recognized that variation occurs due to differences in

land management practices, as the samples were

collected from different farm land with different

owners. Variations in land management practices

may result in a significant difference in yields

although the land parcels under consideration have

similar biophysical characteristics.

It is argued that attempts to correlate land

potential (expressed in form of land suitability

indices) with crop yields only, may not always result

in a good representation of the land performance.

The main reason is that data on crop yields are not

readily available, particularly in undeveloped

regions; or on the other hand, most available

agricultural production data are not well geo-

referenced. However, this experiment has

successfully designed a methodological framework

where crop yields were collected from 31 farm lands

(involving 31 land owners) during March to June

cultivation period.

Furthermore, assuming that the data sets are

accompanied by spatial geo-references, details of

land management such as fertilizers, irrigation,

weeding, date of planting, etc. should also be taken

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

438

into account. In this experiment, such phenomenon

has suppressed correlation coefficient. Differences

in land management may lead to yield differences

between farms especially between the best and the

worst management practices.

3.4 Yield Mapping

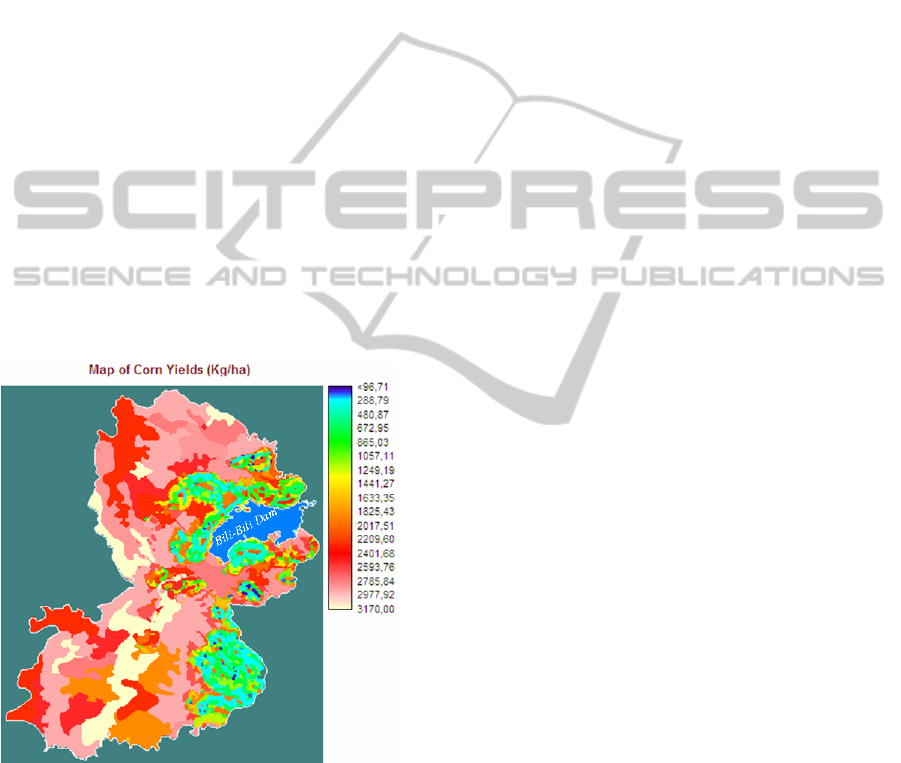
Using the formula in equation (5), potential yield

(kg/ha) of corn (Zea mays L.) in the study area is

then extrapolated and mapped in Geographic

Information Systems (GIS) (Figure 7). This map

depicts spatial distribution of corn yields (kg/ha)

across the study area under crop management

currently practiced in this region. The map shows

that land with relatively high crop yields is found

around the flood plains, where most paddy field

exists. Land parcels with low yields are mostly

located in the higher altitude eastern sections of the

study area. The map shows that with existing crop

management, the maximum possible production of

corn in the region is 3170 kg/ha, with the averaged

figure of about 2500 kg/ha. This is somewhat above

the averaged corn production in South Sulawesi

Province, which is of 2200 kg/ha.

Figure 7: Map of potential yield (kg/ha) of corn (Zea mays

L.) in the study area.

In terms of future crop management to improve

corn yield in the study area, spatial segmentation as

seen in Figure 7 can assist the land managers or

decision makers in the allocation of different types

of land and crop management. The areas having a

high potential yield (as in the western sections of the

study area) needs only a low input management to

achieve optimal yields, while land parcels with

relatively low potential yield (as in the eastern

sections) will need medium to high input. The map

is also useful for designing a spatial planning

program in a regional level for optimal decision

making in land use and land management.

4 CONCLUSIONS

Based on the study on using fuzzy set methodology

and intensive field work, it can be concluded that:

 Use of fuzzy set modeling approaches has

resulted in a cell-by-cell land potential map for

developing corn in the study region.

 An indication of correlation exists between land

quality (in form of LSI) and corn yield in the field,

and variation in the scatter diagram gives insights

into differences in existing land and crop

management in the study area.

 This experiment has shown potential use of

fuzzy modeling procedures combined with a

regression model to map the potential yield at a

regional level, and this can assist in setting up

regional-based agricultural programs especially corn

development.

 It becomes obvious that the results of analyses

here not only show how the relationships between

two sets of data can be examined in a continuous

(fuzzy) manner, but also illustrate the significance of

using fuzzy set approaches for micro-mapping, and

fine discriminations of land quality and potential

yield in a large scale corn-based program.

ACKNOWLEDGEMENTS

Financial support provided by The Ministry of Riset

and Technology, and The Directorate of Higher

Education, Republic of Indonesia is highly

appreciated.

REFERENCES

Baja, S., Chapman, D. M., and Dragovich, D., 2002a. A

conceptual model for defining and assessing land

management units using a fuzzy modelling approach

in GIS environment. Environmental Management, Vol.

29: 647-661.

Baja, S., Chapman, D. M. and Dragovich, D., 2002b.

Using GIS-based continuous methods for assessing

agricultural land use potential in sloping areas.

SPATIAL-BASED FUZZY CLASSIFICATION OF LAND SUITABILITY INDEX FOR AGRICULTURE

DEVELOPMENT - A Model Validation Perspective

439

Environment and Planning B: Planning and Design,

Vol. 29: 3-20.

Baja, S, Dragovich, D. and Chapman, D., 2007. Spatial

Based Compromise Programming for Multiple Criteria

Decision Making Modeling in Land Use Planning.

Environmental Modelling and Assessment Vol. 12:

171-184.

Burrough, P. A, and McDonnell, R. A., 1998. Principles

of Geographical Information Systems. Oxford

University Press Inc., New York.

Burrough, P. A., MacMillan, R. A. and van Deursen, W.,

1992. Fuzzy classification methods for determining land

suitability from soil profile observations and topography.

Journal of Soil Science, 43: 193-210.

Cook, S. E., and Bramley, R. G. V., 2001. Is agronomy

being left behind by precision agriculture? In

Proceedings of the 10th Australian Agronomy

Conference, Hobart, 28 January -1 February. (ASA:

Hobart).

Davidson, D. A., Theocharopoulos, S. P. and Bloksma, R.

J., 1994. A land evaluation project in Greece using

GIS and based on Boolean and fuzzy set

methodologies. International Journal of Geographic

Information Systems, 8: 369-384.

Harrison, S. R., 1991. Validation of agricultural expert

system. Agricultural Systems, Vol. 35: 265-285.

Maeda, S., Kawachi, T., Unami, K., Takeuchi, J., Izumi,

T., and Chono, S., 2009. Fuzzy optimization model for

integrated of total nitrogen loads from distributed and

nonpoint sources in watershed. Paddy Water Environ

Vol. 7:163–175.

Olano, J. M., Loidi, J. J., Alez, A. G., and Escudero, A.,

1998. Improving the interpretation of fuzzy partitions

in vegetation science with constrained ordinations.

Plant Ecology Vol. 134: 113–118.

Zadeh, L. A., 1965. Fuzzy sets. Information and Control,

8: 338-353.

APPENDIX

Appendix 1: Evaluation criteria of land suitability for corn.

Land characteristics

Limitation degree**

0 1 2 3 4

Site drainage well moderate imperfect

Poor & very

poor

Soil texture and structure*

Z, ZL, ZCL, ZCs, SCs,

CSs, Cs, CLs, Ls

SCL, SCm, ZCm, Cm,

HCs, CLm, CSm, Lm

HCm, SL, SCLm,

S Sm

Solum depth very deep deep moderate shallow very shallow

Cation exchange capacity, CEC

(topsoil)

high – very high moderate low – very low -

Organic matter, OM (topsoil) very high high moderate

low – very

low

pH (1:5 soil:water) 5.5 - 8.0

5.1 - 5.5 and

8.1 - 8.5

4.5 - 5.0 and

8.6 - 9.0

< 4.5 and

9.1 - 9.5

Slope gradient (%) < 2 2 - 8 8 - 16 16 - 25 > 25

Rainfall (mm/annum) 500 – 1200

1200 – 1600

400 – 500

>1600

300 – 400

< 300 -

Note: *Texture: C = Clay, CL= Clay loam, CS = Clayey sand, HC = Heavy clay, L = Loam, LS = Loamy sand, S = Sand, SC = Sandy

clay, SCL = Sandy clay loam, SL = Sandy loam, Z = Silt, ZC = Silty clay, ZCL = Silty clay loam, ZL = Silt loam; Structure: s =

Structured, m = Massive (or apedal).

**Limitation degree: 0=None, 1=Slight, 2=Moderate, 3=Severe, 4=Very severe

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

440