TIME SERIES SEGMENTATION AS A DISCOVERY TOOL

A Case Study of the US and Japanese Financial Markets

Jian Cheng Wong

, Gladys Hui Ting Lee

, Yiting Zhang

, Woei Shyr Yim

, Robert Paulo Fornia

Danny Yuan Xu

, Jun Liang Kok

and Siew Ann Cheong

Division of Mathematical Sciences, School of Physical and Mathematical Sciences, Nanyang Technological University

21 Nanyang Link, Singapore 637371, Republic of Singapore

University of Colorado at Boulder, Boulder, CO 80309, U.S.A.

Bard College, PO Box 5000, Annandale-on-Hudson, NY 12504, U.S.A.

Division of Physics and Applied Physics, School of Physical and Mathematical Sciences

Nanyang Technological University, 21 Nanyang Link, Singapore 637371, Republic of Singapore

Keywords:

Time series segmentation, Coarse graining, Macroeconomic cycle, Financial markets.

Abstract:

In this paper we explain how the dynamics of a complex system can be understood in terms of the low-

dimensional manifolds (phases), described by slowly varying effective variables, it settles onto. We then

explain how we can discover these phases by grouping the large number of microscopic time series or time

series segments, based on their statistical similarities, into the a small number of time series classes, each

representing a distinct phase. We describe a speciﬁc recursive scheme for time series segmentation based on

the Jensen-Shannon divergence, and check its performance against artiﬁcial time series data. We then apply

the method on the high-frequency time series data of various US and Japanese ﬁnancial market indices, where

we found that the time series segments can be very naturally grouped into four to six classes, corresponding

roughly with economic growth, economic crisis, market correction, and market crash. From a single time

series, we can estimate the lifetimes of these macroeconomic phases, and also identify potential triggers for

each phase transition. From a cross section of time series, we can further estimate the transition times, and

also arrive at an unbiased and detailed picture of how ﬁnancial markets react to internal or external stimuli.

1 MOTIVATION

Most problems we seek urgent answers to presently

are associated with complex systems. This include

climate change (Giorgi and Mearns, 1991; Wang

et al., 2004; Garnaut, 2008), renewable energy (Din-

cer, 2000; Gross et al., 2003), infectious diseases

(Morens et al., 2004; Leach et al., 2010), global ﬁ-

nancial crises (Crotty, 2009; Taylor, 2009), and even

global terrorism (Monar, 2007; Fellman, 2008). Com-

plex systems are so named because their constituent

degrees of freedom are constantly interacting at all

scales, generating at each scale emergent dynamical

structures which cannot be understood in terms of the

structures at the previous scale. To map out the entire

hierarchy of behaviors in a complex system, we must

therefore learn about its behaviors at all levels.

This seems like a terrifying task, if we always try

to understand such behaviors in terms of all the mi-

croscopic variables. However, we understand from

nonlinear dynamics that nature is generally kind on

us. Instead of all microscopic variables taking on all

possible values as the system evolves in time, we fre-

quently ﬁnd them strongly limiting the values each

other can take, because of their mutual interactions.

When this happens, we say that the system has settle

onto a low-dimensional manifold, which can be de-

scribed using a small number of effective variables.

Each of these effective variables is a large collection

of microscopic variables. From the point of view

of statistical thermodynamics, each low-dimensional

manifold represents a distinct macroscopic phase.

For example, a macroscopic collection of water

molecules can be found in three distinct phases. Be-

low the critical temperature and pressure, liquid water

and water vapor can be distinguished by their densi-

ties. Liquid water and solid ice can also be easily dis-

tinguished by their pair distribution functions, whose

Fourier transforms can be easily probed using exper-

imental techniques like X-ray diffraction or neutron

scattering. But what if we do not know all these be-

forehand, and only have time series data on the water

molecule displacements. Can we still conclude that

water has three distinct phases?

Cheng Wong J., Hui Ting Lee G., Zhang Y., Shyr Yim W., Paulo Fornia R., Yuan Xu D., Liang Kok J. and Ann Cheong S..

TIME SERIES SEGMENTATION AS A DISCOVERY TOOL - A Case Study of the US and Japanese Financial Markets.

DOI: 10.5220/0003653700520063

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 52-63

ISBN: 978-989-8425-79-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

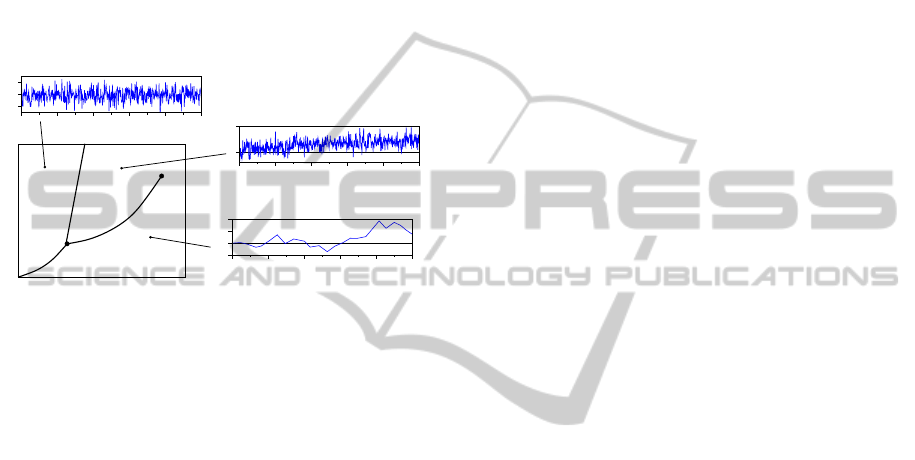
From Figure 1, we see that the answer is afﬁrma-

tive. In solid ice, the displacement of a given wa-

ter molecule ﬂuctuates about an average point. This

ﬂuctuation becomes stronger with increasing temper-

ature, but is time-independent. In liquid water at

comparable temperatures, there are also strong dis-

placement ﬂuctuations. However, in addition to being

temperature dependent, the ﬂuctuations are also time

dependent. This is because in liquid water, molecu-

lar trajectories are diffusive. Finally, in water vapor,

molecular trajectories are ballistic, allowing us to dis-

tinguish it from liquid water.

0 100 200 300 400

500

−2

δr

0 100 200 300 400

500

−50

100

δr

0 100 200 300 400

500

δr

temperature

pressure

solid

liquid

gas

(a)

(b)

(c)

Figure 1: A typical phase diagram showing where the solid,

liquid, and gas phases of a substance occurs in the pressure-

temperature (p-T ) plane. Also shown in the ﬁgure are the

equilibrium ﬂuctuations δr in the displacement of a given

atom in the (a) solid phase, with time-independent vari-

ance h|δr|

i ∝ T ; (b) liquid phase, with a diffusive variance

h|δr|

i ∝ t; and (c) gas phase, with long ballistic lifetimes.

Based on the above discussions, we see that it is

possible to discover the phases of water starting from

only microscopic time series, since we know before-

hand how these will be different statistically. But

since it is simple statistics that differentiate phases,

we can also discover them without any prior knowl-

edge. If the system has gone through multiple phase

transitions, we can detect these transitions by per-

forming time series segmentation, which partitions

the time series into a collection of segments statis-

tically distinct from their predecessors and succes-

sors. If we then cluster these time series segments,

we should be able to very naturally classify them into

three clusters, each representing one phase of wa-

ter. Alternatively, if we have many time series, some

of which are in the solid phase, others in the liquid

phase, and the rest in the gas phase, we can directly

cluster the time series to ﬁnd them falling naturally

into three groups. The various methods for doing so

are known as time series clustering.

These considerations are very general, and can be

applied to diverse complex systems. Apart from the

ﬁnancial markets we report in this paper, we also ap-

ply the two methods to understanding atmospheric

dynamics, climate change, earthquakes, the melting

of metallic nanoclusters (Lai et al., 2011), and protein

folding. While we are not the ﬁrst to apply time series

segmentation and time series clustering to such sys-

tems (Vaglica et al., 2008; T

oth et al., 2010; Bialonski

and Lehnertz, 2006; Lee and Kim, 2006; Santhanam

and Patra, 2001; Bivona et al., 2008), our contribution

in this paper lies with the framing and elucidating of

how the two methods ﬁt into the hierarchy of knowl-

edge discovery processes. In this paper, we focus

on describing the time series segmentation method in

Section 2, and how it can be applied to gain insights

into the behavior of ﬁnancial markets in Section 3.

We then conclude in Section 4.

2 METHODS

2.1 Optimized Recursive Segmentation

We start off with a time series x = (x

,. . . ,x

) which

is statistically nonstationary. This means that statisti-

cal moments like the average and variance evaluated

within a ﬁxed window at different times are also ﬂuc-

tuating. However, we suspect that x might consist of

an unknown number M of stationary segments from

an unknown number P of segment classes. Since it is

possible to arrive at reasonable estimates of M with-

out knowing what P is, we will determine these two

separately. The problem of ﬁnding M is equivalent to

ﬁnding the positions of the M −1 segment boundaries.

This is the sequence segmentation problem (Carlstein

et al., 1994; Chen and Gupta, 2000), which has been

studied in many different ﬁelds, for example, in im-

age segmentation (Barranco-L

opez et al., 1995), bi-

ological sequence segmentation (Braun and M

uller,

1998), medical time series analysis (Bernaola-Galv

et al., 2001), econometrics (Goldfeld and Quandt,

1973; Hamilton, 1989) and ﬁnancial time series seg-

mentation (Oliver et al., 1998; Chung et al., 2002;

Lemire, 2006; Jiang et al., 2007).

There are three rigorous approaches to to time

series and sequence segmentation: (i) dynamic pro-

gramming (Braun et al., 2000; Ramensky et al.,

2000); (ii) entropic segmentation (Bernaola-Galv

et al., 1996; Rom

an-Rold

an et al., 1998); and (iii) hid-

den Markov model (HMM) segmentation (Churchill,

1989; Churchill, 1992). Dynamic programming is

very efﬁcient for discrete sequences with small alpha-

bets, but not suited to time series of continuous vari-

ables. HMM segmentation is popular in the bioinfor-

matic community, but requires assumptions on how

many segment types there will be. It is also inefﬁ-

cient if the HMM has to be estimated alongside the

TIME SERIES SEGMENTATION AS A DISCOVERY TOOL - A Case Study of the US and Japanese Financial Markets

segmentation. Entropic segmentation is a broad class

of information-theoretic methods that include pattern

recognition techniques. For our study, we adopted

the recursive entropic segmentation scheme proposed

by Bernaola-Galv

an and coworkers (Bernaola-Galv

et al., 1996; Rom

an-Rold

an et al., 1998) for biolog-

ical sequence segmentation. For a time series of a

continuous variable, we assume that all its segments

are generated by Gaussian processes, i.e. within seg-

ment m, x

(m)

are normally distributed with mean µ

and variance σ

. Other distributions can be used,

depending on what is already known about the time

series statistics, how easy or hard parametrization is,

and how easy or hard it is to calculate the probability

distribution function. We chose Gaussian models for

each segment because their parameters are easy to es-

timate, and their probability distribution functions are

easy to calculate.

Given x = (x

,. . . ,x

), we ﬁrst compute its one-

segment likelihood

∏

i=1

√

2πσ

exp



−

−µ)

2σ



(1)

assuming that the entire time series is sampled from

a normal distribution with mean µ and variance σ

Next, we assume that x = (x

,. . . ,x

t+1

,. . . ,x

) ac-

tually consists of two segments x

= (x

,. . . ,x

), sam-

pled from a normal distribution with mean µ

and

variance σ

, and x

= (x

t+1

,. . . ,x

) sampled from

a normal distribution with mean µ

and variance σ

The two-segment likelihood of x is thus

(t) =

∏

i=1

2πσ

exp



−

−µ

)

2σ



∏

j=t+1

2πσ

exp



−

−µ

)

2σ



. (2)

Taking the logarithm of the ratio of likelihoods, we

obtain the Jensen-Shannon divergence (Lin, 1991)

∆(t) = ln

(t)

. (3)

This is N times the more general deﬁnition

∆(P

) = H(π

+ π

) −π

H(P

) −π

H(P

)

of the Jensen-Shannon divergence, with π

= N

/N,

= N

/N, and H(P) is the Shannon entropy for

the probability distribution P. The Jensen-Shannon

divergence so deﬁned measures how well the two-

segment model ﬁts the observed time series over the

one-segment model. In practice, the Gaussian param-

eters µ,µ

,µ

,σ

appearing in the likelihoods

are replaced by their maximum likelihood estimates

ˆµ, ˆµ

, ˆµ

, and

To ﬁnd the best segment boundary t

∗

to cut x into

two segments, we run through all t, and pick t = t

∗

such that

∆

max

= ∆(t

∗

) = max

∆(t), (4)

as shown in Figure 2. At t = t

∗

, the left and right seg-

ments are the most distinct statistically. We call ∆(t

∗

)

the strength of the segment boundary at t = t

∗

. To ﬁnd

more segment boundaries, we repeat this one-to-two

segmentation procedure for x

and x

, and all sub-

sequent segments. As the segments get shorter, the

divergence maxima of new segment boundaries will

also get smaller. When these divergence maxima be-

come too small, the new segment boundaries will no

longer be statistically signiﬁcant. Further segmenta-

tion thus becomes meaningless.

1997 1998 1999 2000 2001 2002 2003 2004

2005 2006

2007 2008

500

1000

1500

2000

Jensen-Shannon divergence

500

1000

1500

2000

2500

(a)

(b)

Figure 2: Jensen-Shannon divergence spectrum of the Dow

Jones Industrial Average index time series between January

1997 and August 2008 (red), based on which we identify (a)

the ﬁrst segment boundary to be around the middle of 2003

(marked by red vertical line). To further segment the left

and right subsequences, we compute the Jensen-Shannon

divergence spectra (green and blue respectively) entirely

within the respective subsequences, and (b) ﬁnd the loca-

tions of their divergence maxima.

There are three approaches to terminating the re-

cursive segmentation in the literature. In the orig-

inal approach by Bernaola-Galv

an and coworkers

(Bernaola-Galv

an et al., 1996; Rom

an-Rold

an et al.,

1998), the divergence maximum of a new segment

boundary is tested for statistical signiﬁcance against

a χ

distribution whose degree of freedom depends

on the length of the segment to be subdivided. Recur-

sive segmentation terminates when no new segment

boundaries more signiﬁcant than the chosen conﬁ-

dence level can be found. In the second approach

(Li, 2001b; Li, 2001a), a segment is subdivided

if the information criterion of its best two-segment

model exceeds that of its one-segment model. Re-

cursive segmentation terminates when further seg-

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

mentation does not explain the data better. In the

third approach (Cheong et al., 2009b), we compare

the Jensen-Shannon divergence ∆(t) against a coarse-

grained divergence

∆(t) of the segment to be subdi-

vided, to compute the total strength of point-to-point

ﬂuctuations in ∆(t). Recursive segmentation termi-

nates when the area under

∆(t) falls below the desired

signal-to-noise ratio. The most statistically signiﬁcant

segment boundaries will all be discovered using any

of the three termination criteria.

Based on the experience in our previous work

(Wong et al., 2009), these most statistically signiﬁ-

cant segment boundaries are also discovered if we ter-

minate the recursive segmentation when no new opti-

mized segment boundaries with Jensen-Shannon di-

vergence greater than a cutoff of ∆

= 10 are found.

This simple termination criterion sometimes result in

long segments whose internal segment structures are

masked by their contexts (Cheong et al., 2009a). For

these long segments, we progressively lower the cut-

off ∆

until a segment boundary with strength ∆ > 10

appears. The ﬁnal segmentation then consists of seg-

ment boundaries discovered through the automated

recursive segmentation, as well as segment bound-

aries discovered through progressive reﬁnement of

overly long segments.

At each stage of the recursive segmentation, we

also perform segmentation optimization, using the al-

gorithm described in Cheong et al. (2009b). Given M

segment boundaries {t

,. . . ,t

}, some of which are

old, and some of which are new, we optimize the po-

sition of the mth segment boundary by computing the

Jensen-Shannon divergence spectrum within the su-

persegment bounded by the segment boundaries t

m−1

and t

m+1

, and replace t

by t

∗

, where the superseg-

ment Jensen-Shannon divergence is maximized. We

do this iteratively for all M segment boundaries, until

all segment boundaries converge to their optimal po-

sitions. This optimization step is necessary, because

of the context sensitivity problem discussed in Cheong

et al. (2009a). Otherwise, statistically signiﬁcant seg-

ment boundaries are likely to be masked by the con-

text they are embedded within, and missed by the seg-

mentation procedure.

2.2 Hierarchical Clustering

After the recursive segmentation terminates, we typi-

cally end up with a large number of segments. Neigh-

boring segments are statistically distinct, but might be

statistically similar to distant segments. We can group

statistically similar segments together, to estimate the

number P of time series segment classes. Various sta-

tistical clustering schemes can be used to achieve this

(see for example, the review by Jain, Murty and Flynn

(Jain et al., 1999), or texts on unsupervised machine

learning). Since the number of clusters is not known

beforehand, we chose to perform agglomerative hier-

archical clustering, using the complete link algorithm.

The statistical distances between segments are given

by their Jensen-Shannon divergences.

103

31.3

104

100

739.1

112

102

105

249.3

42.7

107

115

114

116

109

111

102.2

34.4

110

101

106

108

113

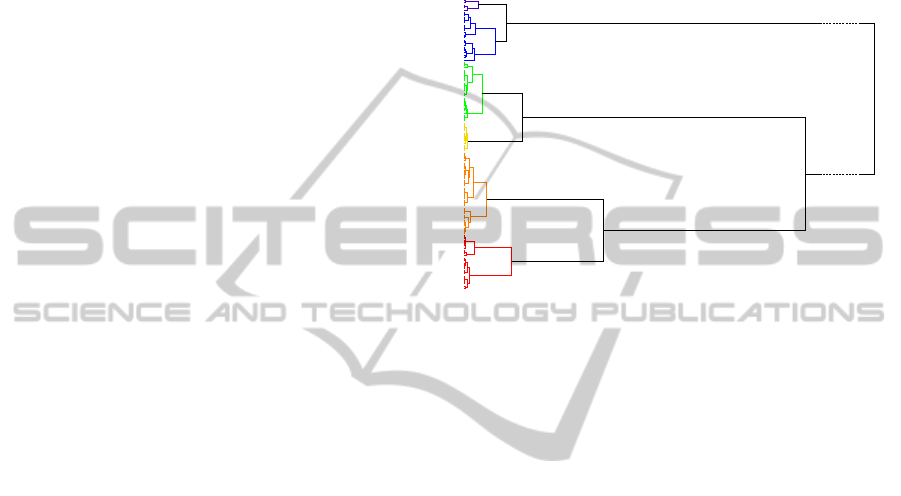
Figure 3: The complete-link hierarchical clustering tree of

the Dow Jones Industrial Average index time series seg-

ments assuming that the index movements within each seg-

ment are normally distributed. The differentiated clusters

are coloured according to their standard deviations: low

(deep blue and blue), moderate (green), high (yellow and

orange), and extremely high (red). Also shown at the ma-

jor branches are the Jensen-Shannon divergence values at

which subclusters are merged.

In Figure 3, we show the hierarchical clustering

tree for the Dow Jones Industrial Average index time

series segments, which tells us the following. If we

select a global threshold ∆ > 739.1, we end up with

one cluster, whereas if we select a global threshold

249.3 < ∆ < 739.1, we ﬁnd two clusters. These clus-

ters are statistically robust, because they are not sen-

sitive to small variations of the global threshold ∆.

However, they are not as informative as we would

like them to be. Going to a lower global threshold

of ∆ = 30, we ﬁnd seven clusters. These seven clus-

ters give us a more informative dynamical picture, but

some of the clusters are not robust. If instead of a

global threshold for all robust clusters, we allow local

thresholds, i.e. ∆ = 30 to differentiate the deep blue

and blue clusters, the green and yellow clusters, and

∆ = 40 to differentiate the orange and red clusters, we

will ﬁnd six natural and robust clusters.

These clusters are differentiated by their standard

deviations, with deep blue being the lowest, and red

being the highest. Based on the actual magnitudes

of the standard deviations (also called market volatili-

ties in the ﬁnance literature), we can also group the

time series segments into four clusters: low (deep

TIME SERIES SEGMENTATION AS A DISCOVERY TOOL - A Case Study of the US and Japanese Financial Markets

blue and blue), moderate (green), high (yellow and

orange), and extremely high (red). As we will ex-

plain in Section 3, these four clusters have very natu-

ral interpretations as the growth (low-volatility), cor-

rection (moderate-volatility), crisis (high-volatility),

and crash (extremely-high-volatility) macroeconomic

phases.

2.3 Validation against Synthetic Data

To test the segmentation scheme, we perform several

numerical experiments on artiﬁcial Gaussian time se-

ries. First, we set the standard deviations of the two

5,000-long segments to σ

= σ

= 1.0. We also ﬁx

the mean of the left segment at µ

= 0, and vary the

mean µ

of the right segment. As we can see from

Table 1(a), the segmentation scheme found only the

single segment boundary at t

∗

= 5000, for a differ-

ence in mean as small as ∆µ = |µ

−µ

| = 0.1. This

is remarkable, because the standard deviations of both

segments are σ

= σ

= 1.0 > ∆µ. As expected,

the standard error for the boundary position decreases

with increasing ∆µ.

Table 1: Positions and standard errors of the segment

boundary discovered using the Jensen-Shannon divergence

segmentation scheme, from 1,000 artiﬁcial Gaussian time

series. In (a) and (b), we set N

= N

= 5, 000, (µ

,σ

) =

(0,1), σ

= 1, and vary µ

. In (b), we set N

= N

= 5,000,

(µ

,σ

) = (0, 1), µ

= 0, and vary σ

. In (c), we set

(µ

,σ

) = (0,1), (µ

= 0, σ

) = (0,0.5), and vary N =

+ N

(a)

∗

±∆t

∗

0.1 4990 ±680

0.2 4980 ±500

0.5 5000 ±490

1.0 4990 ±260

2.0 5010 ±330

5.0 5020 ±410

10.0 5000 ±270

(b)

∗

±∆t

∗

0.1 5000 ±380

0.2 5000 ±350

0.3 5010 ±480

0.4 5020 ±420

0.5 5000 ±280

0.7 5010 ±320

0.9 5000 ±550

(c)

N t

∗

±∆t

∗

100 49 ±7

200 98 ±9

500 249 ±15

1000 497 ±41

2000 998 ±28

5000 2500 ±200

10000 5000 ±290

Next, we set µ

= µ

= 0, ﬁx σ

= 1.0, and vary

. Again, as we can see from Table 1(b), the single

boundary at t

∗

= 5000 was found for ratio of stan-

dard deviations as close to one as σ

/σ

= 0.9. As

expected, the standard error for the boundary position

decreases with increasing disparity between σ

and

. Finally, we set (µ

,σ

) = (0,1) and (µ

,σ

) =

(0,0.5), and vary the length N of the artiﬁcial time

series, always keeping the segment boundary in the

middle. From Table 1(c), we see that the boundary

position is very accurately determined for time series

as short as N = 100. We also see the standard error

growing much slower than N.

Following this, we recursively segmented 10,000

artiﬁcial Gaussian time series of length N = 1000,

each consisting of the same 10 segments shown in Ta-

ble 2. We also see in Table 2 that eight of the nine seg-

ment boundaries were accurately determined. The po-

sition of the remaining boundary, between segments

m = 4 and m = 5, has a large standard error because

it separates two segments that are very similar statis-

tically.

Table 2: The ten segments of the N = 10,000 artiﬁcial

Gaussian time series, and the segment boundaries obtained

using the recursive Jensen-Shannon divergence segmenta-

tion scheme.

m start end µ

∗

±∆t

∗

1 1 1500 0.55 0.275 1497 ±60

2 1501 2500 0.05 0.025 2500 ±14

3 2501 3500 0.20 0.10 3504 ±50

4 3501 5000 0.60 0.30 5010 ±140

5 5001 6501 0.65 0.325 6497 ±39

6 6501 7000 0.30 0.15 7002 ±26

7 7001 8500 0.45 0.225 8500 ±12

8 8501 9000 0.05 0.025 9001 ±12

9 9001 9500 0.45 0.225 9500 ±9

10 9501 10000 0.15 0.075 -

Finally, we timed the MATLAB code that we used

to implement the recursive segmentation. The spatial

complexity of this scheme is O(N), since we need to

store the original time series and two other processed

data arrays of the same length. The temporal com-

plexity of the scheme, however, cannot be easily an-

alyzed, because it depends on how many optimiza-

tion iterations are needed, and how many segment

boundaries are to be discovered. On a MacBook Pro

with 2.4-GHz core-2 duo and 4-GB 1067-MHz DDR3

memory, the two-segment time series took 1±1 ms to

segment, for N = 100, and 63 ±5 ms to segment, for

N = 10000. The 10-segment time series with length

N = 10,000 took 0.38 ±0.03 s to segment, or 42 ±3

ms for each boundary. We also segmented 30 50,000-

point time series from a molecular dynamics simula-

tion of penta-analine. 7084 boundaries were found

after 114 s, which works out to 16 ms per boundary.

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

3 CASE STUDY

3.1 Single US Time Series

For the single time series study, we chose the Dow

Jones Industrial Average (DJI) index. This is a

price-weighted average of the stock prices of the

30 most well capitalized US companies. Tic-by-tic

data between 1 January 1997 and 31 August 2008

for this index was downloaded from the Thomson-

Reuters Tickhistory database (formerly SIRCA

Taqtic, https://tickhistory.thomsonreuters.

com/TickHistory/login.jsp), and processed into

a half-hourly index time series X = (X

,. . . ,X

From X, we then obtain the half-hourly index move-

ment time series x = (x

,. . . ,x

), where x

t+1

−X

and n = N −1, which we assume consists of

M statistically stationary segments. The half-hourly

data frequency was chosen so that we can reliably

identify segments as short as a single day. We do not

go to higher data frequencies, because we are not in-

terested in intraday segments.

As reported in Wong et al. (2009), the clustered

segments of the DJI tell very interesting stories when

we plot how they are distributed over the January

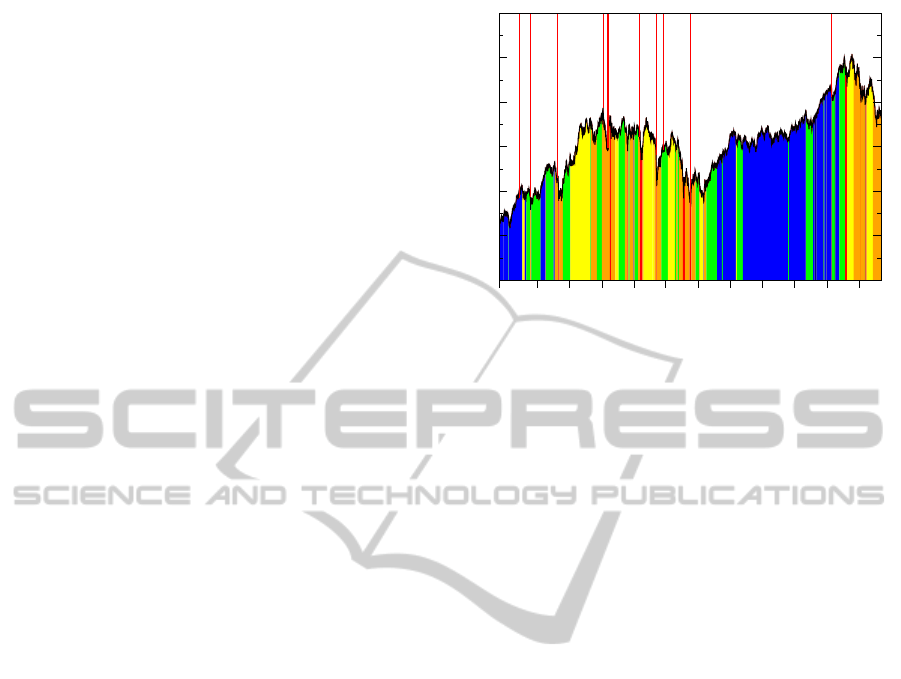
1997 to August 2008 period. From Figure 4, we see

that the DJI (as a proxy for the US economy as a

whole) spends most of its time in the low-volatility

phase (dark blue and blue) and the high-volatility

phase (yellow and orange). Based on when it oc-

curs, we can associate the low-volatility phase with

economic expansion. We also see that the previous

March to November 2001 economic contraction for

the US is completely nested within the high-volatility

phase. This suggests that the high-volatility phase

has the natural interpretation as an economic crisis

phase, which lasts longer than most ofﬁcial reces-

sions. Interrupting both the low-volatility and high-

volatility phases, we also ﬁnd short-lived moderate-

volatility phases (green), which we can therefore

interpret as market corrections. In addition, even

shorter-lived extreme-high-volatility phases (red) can

be found almost exclusively within the high-volatility

phase. These can be unambiguously associated with

market crashes.

More importantly, the temporal distribution tells

us that the US economy, as measured by the DJI, went

into a ﬁve-year crisis period starting in mid-1998, be-

fore recovering in mid-2003. The US economy then

enjoyed a remarkable four-year period of sustained

growth, before succumbing to the Subprime Crisis in

mid-2007. We also see in the temporal distribution the

existence of year-long series of precursor shocks pre-

ceding each transition. These precursor shocks sug-

1997 1998 1999 2000 2001 2002 2003 2004

2005 2006

2007 2008

4000

6000

8000

10000

12000

14000

16000

DJI

1 2 3 4 5 6 7 8 9 10

Figure 4: Temporal distributions of the clustered segments

superimposed onto the DJI time series. The red solid lines

indicate the dates of important market events: (1) July 1997

Asian Financial Crisis; (2) October 1997 Mini Crash; (3)

August 1998 Russian Financial Crisis; (4) DJI 2000 High;

(5) NASDAQ Crash; (6) start of 2001 recession; (7) Sep 11

Attack; (8) end of 2001 recession; (9) DJI 2002 Low; (10)

February 2007 Chinese Correction.

gest on the surface that the July 1997 Asian Finan-

cial Crisis triggered the previous crisis, whereas mar-

ket corrections in the Chinese markets, which started

in May 2006, triggered the present crisis. Further-

more, the mid-2003 economic recovery is preceded

by a year-long series of inverted shocks after the 2002

lows. Therefore, if the fundamental dynamics behind

the US economy had not changed from 2002 to 2009,

we expect from this single time series study that the

US economy will emerge from the global ﬁnancial

crisis one year after the March 2009 lows, i.e. shortly

after the ﬁrst quarter of 2010. In contrast, the US

National Bureau of Economic Research (NBER) an-

nounced in Sep 2010 that the US economic recession

ended in Jun 2009.

3.2 Cross Section of US Time Series

The story of the US economy becomes even richer

and more interesting, when we do a comparative seg-

mentation and clustering analysis of the ten Dow

Jones US (DJUS) economic sector indices (Lee et al.,

2009). Tic-by-tic data between 14 Feb 2000 and

31 Aug 2008 for these ten indices (see Table 3)

were downloaded from the Thomson-Reuters Tick-

History database. Since different indices have differ-

ent magnitudes, we processed the raw data ﬁrst into

half-hourly time series X

= (X

i,1

i,2

,. . . ,X

i,N

) for

each of the ten indices i = 1, . ..,10, before obtain-

ing the half-hourly log-index movement time series

= (y

i,1

i,2

,. . . ,y

i,n

), i = 1,...,10, n = N −1, where

i,t

= ln X

i,t+1

−lnX

i,t

for more meaningful compari-

TIME SERIES SEGMENTATION AS A DISCOVERY TOOL - A Case Study of the US and Japanese Financial Markets

son between the indices.

Table 3: The ten Dow Jones US economic sector indices.

i symbol sector

1 BM Basic Materials

2 CY Consumer Services

3 EN Energy

4 FN Financials

5 HC Healthcare

6 IN Industrials

7 NC Consumer Goods

8 TC Technology

9 TL Telecommunications

10 UT Utilities

The ﬁrst interesting observation we make is that

the time it takes for the US economy to recover from

a ﬁnancial crisis (one-and-a-half years, Figure 5(a))

and that for it to completely enter a ﬁnancial crisis

(two months, Figure 5(b)) are very different in scale.

For the mid-2003 US economic recovery, the ﬁrst two

sectors to recover are EN and BM, and the last two

sectors to recover are TL and TC. It is reasonable for

EN and BM to recover ﬁrst, since they are at the base

of the economic supply chain. It is also reasonable

that TC and TL were the last sectors to recover, since

the previous ﬁnancial crisis was the result of the tech-

nology bubble bursting. For the mid-2007 US eco-

nomic decline, we ﬁnd some surprises: instead of NC

(which includes homebuilders and realties) and FN

(which includes banks) being responsible for drag-

ging the US economy down, fully half of the DJUS

economic sectors entered the crisis phase before FN.

Guided by this coarse-grained picture of the US

economy’s slow time evolution, we can extract even

more understanding from the high-frequency ﬂuctua-

tions (Zhang et al., 2011). We do this by computing

the linear cross correlations

i j

∑

t=1

i,t

− ¯y

)(y

j,t

− ¯y

)

n−1

∑

t=1

i,t

− ¯y

)

∑

t=1

j,t

− ¯y

)

(5)

between the ten DJUS economic sector indices over

different time intervals. We then look at the mini-

mal spanning tree (MST) representation of the cross-

correlation matrix (Kruskal, 1956; Prim, 1957; Man-

tegna, 1999). The MST shows only the nine strongest

links that do not incorporate cycles into the graph of

the ten US economic sectors.

In this part of our study, we computed the cross-

correlation matrix ﬁrst over the entire time series,

from February 2000 to August 2008. From Figure

6(a), we see that IN, CY and NC, are at the centre of

the MST, while the sectors HC, TC, TL, and UT lie

on the fringe of the MST. This is consistent with the

Figure 5: Temporal distributions of clustered segments for

the time series of all ten US economic sectors (top) between

April 2002 and September 2004, showing the sequence of

recovery from the mid-1998 to mid-2003 ﬁnancial crisis,

and (bottom) between 23 May 2007 and 29 August 2008,

showing the sequence of descent into the present ﬁnancial

crisis.

former group of sectors being of central importance,

and the latter being of lesser importance to the US

economy (Heimo et al., 2009).

We also expect interesting structural differences

between MSTs constructed entirely within the pre-

vious crisis (2001–2002, Figure 6(b)), the previous

growth (2004–2005, Figure 6(c)), and the present cri-

sis (2008–2009, Figure 6(d)). Indeed, we see two dis-

tinct MST topologies: a chain-like MST which occurs

for both crises, and a star-like MST which occurs for

the growth phase. Even though we only have three

data points (two crises and a growth), we believe the

generic association of chain-like MST and star-like

MST to the crisis and growth phases respectively is

statistically robust. Our assessment that the topology

change in the MST is statistically signiﬁcant is further

supported by the observations by Onnela et al., at the

microscopic scale of individual stocks (Onnela et al.,

2003a; Onnela et al., 2003b; Onnela et al., 2003c).

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

EN BM IN

(a)

BM IN

ENUT

NC HC

(b)

EN BM

FN TL

(c)

BM IN

EN HCNCCY

FN UT

(d)

Figure 6: The MSTs of the ten DJUS economic sectors,

constructed using half-hourly time series from (a) February

(d) 2008-2009. The ﬁrst and the third two-year windows,

(b) and (d), are entirely within an economic crisis, whereas

the second two-year window, (c), is entirely within an eco-

nomic growth period.

EN BM

FN TL

INEN BM NC

CY UT

(a) (b)

Figure 7: Comparison of the MSTs for (a) the 2004–

2005 growth period, and (b) the moderate-volatility seg-

ment around September 2009.

Speaking of ‘green shoots’ of economic revival

that were evident in Mar 2009, Federal Reserve chair-

man Ben Bernanke predicted that “America’s worst

recession in decades will likely end in 2009 before a

recovery gathers steam in 2010”. We therefore looked

out for a star-like MST in the time series data of 2009

and 2010. Star-like MSTs can also be found deep in-

side an economic crisis phase, but they very quickly

unravel to become chain-like MSTs. A persistent star-

like MST, if it can be found, is statistical signature

that the US economy is ﬁrmly on track to full re-

covery (which may take up to two years across all

sectors). More importantly, the closer the MST of a

given period is to a star, the closer we are to the ac-

tual recovery. Indeed, the MST is already star-like for

a moderate-volatility segment in Sep 2009 (see Fig-

ure 7), and stayed robustly star-like throughout the

Greek Debt Crisis of May/Jun 2010. The statistical

evidence thus suggests that the US economy started

recovering late 2009, and stayed the course through

2010. Bernanke was indeed prophetic.

3.3 Cross Section of Japanese Time

Series

As a comparison, we also segmented the 36 Nikkei

500 Japanese industry indices (see Table 4) between

1 Jan 1996 and 11 Jun 2010. Tic-by-tic data were

downloaded from the Thomson-Reuters TickHistory

database, and processed into half-hourly index time

series X

= {X

i,1

i,2

,. . . ,X

i,N

}, i = 1, . . .,36. As

with the US cross section study, we then obtain

the half-hourly log-index movement time series y

i,1

i,2

,. . . ,y

i,n

), i = 1,...,36, n = N − 1, where

i,t

= ln X

i,t+1

−ln X

i,t

for more meaningful compar-

ison between the indices.

2002

2003

2004

2005 2006

2007

Figure 8: Temporal distributions of the 36 Nikkei 500

Japanese industry indices from January 2002 to December

2007. In this ﬁgure, the growth segments are colored blue,

correction segments are colored green, crisis segments are

colored yellow or orange, and crash segments are colored

red.

In this paper, we will focus on the 2005 near re-

covery of the Japanese economy, and the 2007 fall of

TIME SERIES SEGMENTATION AS A DISCOVERY TOOL - A Case Study of the US and Japanese Financial Markets

Table 4: The 36 Nikkei 500 industry indices. Each index is

a price-weighted average of stocks which are components of

the Nikkei 500 index. The Nikkei 500 index was ﬁrst cal-

culated on January 4, 1972 with a value of 223.70, and its

500 component stocks are selected from the ﬁrst section of

the Tokyo Stock Exchange based on trading volume, trad-

ing value and market capitalization for the preceding three

years. The makeup of the Nikkei 500 is reviewed yearly,

and each year approximately 30 stocks are replaced.

i symbol industry

1 NAIR Air Transport

2 NAUT Automotive

3 NBKS Banking

4 NCHE Chemicals

5 NCMU Communications

6 NCON Construction

7 NELC Electric Power

8 NELI Electric Machinery

9 NFIN Other Financial Services

10 NFIS Fisheries

11 NFOD Foods

12 NGAS Gas

13 NGLS Glass & Ceramics

14 NISU Insurance

15 NLAN Other Land Transport

16 NMAC Machinery

17 NMED Pharmaceuticals

18 NMIS Other Manufacturing

19 NMNG Mining

20 NNFR Nonferrous Metals

21 NOIL Oil & Coal Products

22 NPRC Precision Instruments

23 NREA Real Estate

24 NRET Retail

25 NRRL Railway/Bus

26 NRUB Rubber Products

27 NSEA Marine Transport

28 NSEC Securities

29 NSPB Shipbuilding

30 NSTL Steel Products

31 NSVC Services

32 NTEQ Other Transport Equipment

33 NTEX Textiles & Apparel

34 NTIM Pulp & Paper

35 NTRA Trading Companies

36 NWHO Warehousing

the Japanese economy to the Subprime Crisis. From

Figure 8, we see that NMNG started growing the ear-

liest, NFIS started growing the latest, while NSPB did

not seem to have grown at all between 2002 and 2005.

We see also that the Japanese economy, led by NMNG

and NELC, took two years and two months to com-

pletely recover from the back-to-back Asian Financial

and Technology Bubble Crises. While the time scales

of complete economic recovery appear to be differ-

ent, very similar industries led the recovery processes

of US and Japan.

Next, we look at how the Japanese economy suc-

Figure 9: Temporal distributions of the 36 Nikkei 500

Japanese industry indices from January 2007 to June 2010.

In this ﬁgure, the growth segments are colored blue, cor-

rection segments are colored green, crisis segments are col-

ored yellow or orange, and crash segments are colored red.

Within this period, we can identify eight corresponding seg-

ments, labeled ‘Subprime1’ to ‘Subprime8’.

cumbed to the Subprime Crisis. As we can see from

Figure 9, the Japanese economy fell in ﬁve stages.

The most important time scale in Japan’s response

to the Subprime Crisis is that associated with stage

2, which appears to be triggered by the start of the

Subprime Crisis in US, and affected 21 out of 36

Nikkei 500 industries. Here, the Subprime Crisis

swept through NISU, NSVC, NRUB to NTEQ in a

mere 27 days. This is half the time it took for the US

economy to fall from ﬁrst to the last economic sector,

with NC (the sector homebuilders belong to) leading

the pack. As late as June 2010, most Japanese in-

dustries were still in the sustained crisis phase. Only

NMNG, NWHO, NTRA, and NRET showed signs

of early recovery from mid 2009 onwards. If the

Japanese economy again takes two and a half years

to completely recover, this will happen in the begin-

ning of 2012.

Finally, we tracked how the MST change going

from one segment to the next during the Subprime

Crisis. In 21st century Japanese economy, NELI,

NMAC, and NCHE are the growth industries, based

on the fact that they are hubs consistently in all or

most of the MSTs. NNFR and NRRL, which we con-

sider quality industries, also become occasional hubs

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

in the MSTs. In Figure 10, we see the NNFR and

NRRL clusters of industries growing at the expense

of the NCHE and NMAC clusters of industries, as we

go from the Subprime3 period to the Subprime4 pe-

riod. This tells us that the pheripheral industries went

from being most strongly correlated with NCHE and

NMAC to being most strongly correlated with NNFR

and NRRL. We believe this is a signature of money

leaving the NCHE and NMAC industries, and enter-

ing the NNFR and NRRL industries, i.e. a ﬂight to

quality (Connolly et al., 2005; Baur and Lucey, 2009)

from NCHE/NMAC to NNFR/NRRL.

(a)

(b)

Figure 10: MSTs for the (a) Subprime3 period and (b) Sub-

prime4 period. In this ﬁgure, the number beside each link

indicates the order in which the link was added to the MST,

whereas the thicknesses of the links indicate how strong the

correlations are between industries.

4 CONCLUSIONS

To conclude, we have explained how the dynamics

of complex systems self-organize to reside on low-

dimensional manifolds governed by the slow time

evolution of a small set of effective variables. We ex-

plained how these low-dimensional manifolds are re-

lated to thermodynamic phases, how fast ﬂuctuations

of microscopic variables are dictated by which low-

dimensional manifold the system is in. We then ex-

plained how it is possible to discover the phases of a

complex system by statistically classifying the micro-

scopic time series, each class representing a macro-

scopic phase.

Following this, we described in details the time

series segmentation method adapted from the origi-

nal scheme developed by Bernaola-Galv

an et al. for

biological sequence segmentation. In this method,

we examine the Jensen-Shannon divergence spectrum

∆(t) of the given time series, to see how much bet-

ter the data is ﬁtted by two distinct stochastic mod-

els than it is by one stochastic model. The time se-

ries will then be cut into two segments at the point

where ∆(t) is maximized. This one-to-two segmen-

tation is then applied recursively to obtain more and

more segments. At each stage of the recursive seg-

mentation, we optimize the positions of all segment

boundaries. The recursive segmentation is terminated

when the strengths of new segment boundaries fall

below the chose threshold of ∆

= 10. Long seg-

ments are then progressively reﬁned, before we per-

form complete-link hierarchical clustering on the time

series segments to discover the natural number of time

series segment classes.

After a systematic test of the method on artiﬁcial

time series, we performed time series segmentation

on the Dow Jones Industrial Average index time se-

ries, the ten Dow Jones US Economic Sector indices,

and the 36 Nikkei 500 Japanese Industry indices, as

a concrete demonstration of its potential for knowl-

edge discovery. From the single time series study,

we found the time series segments very naturally fall

into four to six clusters, which can be roughly asso-

ciated with the growth, crisis, correction, and crash

macroeconomic phases. We also measured the life-

times of the previous US crisis and growth phases to

be about ﬁve years and four years respectively. From

cross section studies, we found that the US economy

took one-and-a-half years to completely recover from

the Technology Bubble Crisis, but only two months to

completely succumb to the Subprime Crisis. In con-

trast, the Japanese economy took two years and two

months to completely recover from the previous cri-

sis, and only 27 days for the Subprime Crisis to com-

pletely set in. For both countries, the previous eco-

nomic recoveries were led by industries at the base of

the economic supply chain.

Guided by the time series segments, we also

analyzed the cross correlations within the US and

Japanese ﬁnancial markets, visualizing these in terms

of MSTs. The MST visualizations allowed us to iden-

tify IN, CY, and NC, NCHE, NELI, and NMAC, to

be the cores of the US and Japanese economies re-

spectively. We detected an early recovery for the US

economy in late 2009, based on the star-like MST

seen at this time. We concluded that the US recovery

TIME SERIES SEGMENTATION AS A DISCOVERY TOOL - A Case Study of the US and Japanese Financial Markets

gained strength, as the MST remained robustly star-

like through the ﬁrst half of 2010. For the Japanese

economy, we identiﬁed ﬂights to quality within the

ﬁnancial markets, and also the lack of clear signs of

recovery as late as Jun 2010.

ACKNOWLEDGEMENTS

This research is supported by startup grant SUG 19/07

from the Nanyang Technological University. RPF

and DYX thank the Nanyang Technological Univer-

sity Summer Research Internship Programme for ﬁ-

nancial support during Jun and Jul 2010.

REFERENCES

Barranco-L

opez, V., Luque-Escamilla, P., Mart

ınez-Aroza,

J., and Rom

an-Rold

an, R. (1995). Entropic texture-

edge detection for image segmentation. Electronic

Letters, 31:867–869.

Baur, D. G. and Lucey, B. M. (2009). Flights and contagion

— an empirical analysis of stock-bond correlations.

Journal of Financial Stability, 5(4):339–352.

Bernaola-Galv

an, P., Ivanov, P. C., Amaral, L. A. N., and

Stanley, H. E. (2001). Scale invariance in the nonsta-

tionarity of human heart rate. Physical Review Letters,

87:168105.

Bernaola-Galv

an, P., Rom

an-Rold

an, R., and Oliver, J. L.

(1996). Compositional segmentation and long-range

fractal correlations in dna sequences. Physical Review

E, 53(5):5181–5189.

Bialonski, S. and Lehnertz, K. (2006). Identifying phase

synchronization clusters in spatially extended dynam-

ical systems. Physical Review E, 74:051909.

Bivona, S., Bonanno, G., Burlon, R., Gurrera, D., and

Leone, C. (2008). Taxonomy of correlations of wind

velocity — an application to the sicilian area. Physica

A, 387:5910–5915.

Braun, J. V., Braun, R. K., and M

uller, H.-G. (2000). Mul-

tiple changepoint ﬁtting via quasilikelihood, with ap-

plication to dna sequence segmentation. Biometrika,

87(2):301–314.

Braun, J. V. and M

uller, H.-G. (1998). Statistical methods

for dna sequence segmentation. Statistical Science,

13(2):142–162.

Carlstein, E. G., M

uller, H.-G., and Siegmund, D. (1994).

Change-Point Problems, volume 23 of Lecture Notes-

Monograph Series. Institute of Mathematical Statis-

tics.

Chen, J. and Gupta, A. K. (2000). Parametric Statistical

Change Point Analysis. Birkh

auser.

Cheong, S.-A., Stodghill, P., Schneider, D. J., Cartinhour,

S. W., and Myers, C. R. (2009a). The context sen-

sitivity problem in biological sequence segmentation.

q-bio/0904.2668.

Cheong, S.-A., Stodghill, P., Schneider, D. J., Cartinhour,

S. W., and Myers, C. R. (2009b). Extending the re-

cursive jensen-shannon segmentation of biological se-

quences. q-bio/0904.2466.

Chung, F.-L., Fu, T.-C., Luk, R., and Ng, V. (2002). Evo-

lutionary time series segmentation for stock data min-

ing. In Proceedings of the IEEE International Confer-

ence on Data Mining 2002 (9–12 Dec 2002, Maebashi

City, Japan), pages 83–90.

Churchill, G. A. (1989). Stochastic models for heteroge-

neous dna sequences. Bulletin of Mathematical Biol-

ogy, 51(1):79–94.

Churchill, G. A. (1992). Hidden markov chains and the

analysis of genome structure. Computers & Chem-

istry, 16(2):107–115.

Connolly, R., Stivers, C., and Sun, L. (2005). Stock

market uncertainty and the stock-bond return rela-

tion. Journal of Financial and Quantitative Analysis,

40(1):161–194.

Crotty, J. (2009). Structural causes of the global ﬁnan-

cial crisis: a critical assessment of the ‘new ﬁnan-

cial architecture’. Cambridge Journal of Economics,

33(4):563–580.

Dincer, I. (2000). Renewable energy and sustainable devel-

opment: a crucial review. Renewable and Sustainable

Energy Reviews, 4(2):157–175.

Fellman, P. V. (2008). The complexity of terrorist networks.

In Proceedings of the 12th International Conference

on Information Visualization (Jul 9–11, 2008).

Garnaut, R. (2008). The Garnaut Climate Change Review.

Cambridge University Press.

Giorgi, F. and Mearns, L. O. (1991). Approaches to the sim-

ulation of regional climate change: A review. Reviews

of Geophysics, 29(2):191–216.

Goldfeld, S. M. and Quandt, R. E. (1973). A markov model

for switching regressions. Journal of Econometrics,

1:3–16.

Gross, R., Leach, M., and Bauen, A. (2003). Progress

in renewable energy. Environment International,

29(1):105–122.

Hamilton, J. D. (1989). A new approach to the economic

analysis of nonstationary time series and the business

cycle. Econometrica, 57:357–384.

Heimo, T., Kaski, K., and Saram

aki, J. (2009). Maximal

spanning trees, asset graphs and random matrix de-

noising in the analysis of dynamics of ﬁnancial net-

works. Physica A, 388:145–156.

Jain, A., Murty, M., and Flynn, P. (1999). Data clustering:

A review. ACM Computing Surveys, 31(3):264–323.

Jiang, J., Zhang, Z., and Wang, H. (2007). A new seg-

mentation algorithm to stock time series based on

pip approach. In Proceedings of the Third IEEE In-

ternational Conference on Wireless Communications,

Networking and Mobile Computing 2007 (21–25 Sep

2007, Shanghai, China), pages 5609–5612.

Kruskal, J. B. (1956). On the shortest spanning subtree of

a graph and the traveling salesman problem. Proceed-

ings of the American Mathematical Society, 7:48–50.

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

Lai, S. K., Lin, Y. T., Hsu, P. J., and Cheong, S. A. (2011).

Dynamical study of metallic clusters using the sta-

tistical method of time series clustering. Computer

Physics Communications, 182:1013–1026.

Leach, M., Scoones, I., and Stirling, A. (2010). Governing

epidemics in an age of complexity: Narratives, poli-

tics and pathways to sustainability. Global Environ-

mental Change, 20(3):369–377.

Lee, G. H. T., Zhang, Y., Wong, J. C., Prusty, M., and

Cheong, S. A. (2009). Causal links in us economic

sectors. arXiv:0911.4763.

Lee, U. and Kim, S. (2006). Classiﬁcation of epilepsy types

through global network analysis of scalp electroen-

cephalograms. Physical Review E, 73:041920.

Lemire, D. (2006). Overﬁtting and time series segmenta-

tion: A locally adaptive solution. arXiv:cs/0605103.

Li, W. (2001a). Dna segmentation as a model selection

process. In Proceedings of the International Confer-

ence on Research in Computational Molecular Biol-

ogy (RECOMB), pages 204–210.

Li, W. (2001b). New stopping criteria for segmenting dna

sequences. Physical Review Letters, 86(25):5815–

5818.

Lin, J. (1991). Divergence measures based on the shannon

entropy. IEEE Transactions on Information Theory,

37(1):145–151.

Mantegna, R. N. (1999). Hierarchical structure in ﬁnancial

markets. The European Physical Journal B, 11:193–

197.

Monar, J. (2007). The eu’s approach post-september 11:

global terrorism as a multidimensional law enforce-

ment challenge. Cambridge Review of International

Affairs, 20(2):267–283.

Morens, D. M., Folkers, G. K., and Fauci, A. S. (2004).

The challenge of emerging and re-emerging infectious

diseases. Nature, 430:242–249.

Oliver, J. J., Baxter, R. A., and Wallace, C. S. (1998). Min-

imum message length segmentation, volume 1394 of

Lecture Notes in Computer Science, pages 222–233.

Springer.

Onnela, J.-P., Chakraborti, A., Kaski, K., and Kert

esz, J.

(2003a). Dynamic asset trees and black monday.

Physica A, 324:247–252.

Onnela, J.-P., Chakraborti, A., Kaski, K., Kert

esz, J., and

Kanto, A. (2003b). Asset trees and asset graphs in

ﬁnancial markets. Physica Scripta, T106:48–54.

Onnela, J.-P., Chakraborti, A., Kaski, K., Kert

esz, J., and

Kanto, A. (2003c). Dynamics of market correlations:

Taxonomy and portfolio analysis. Physical Review E,

68(5):056110.

Prim, R. C. (1957). Shortest connection networks and some

generalizations. The Bell System Technical Journal,

36:1389–1401.

Ramensky, V. E., Makeev, V. J., Roytberg, M. A., and Tu-

manyan, V. G. (2000). Dna segmentation through the

bayesian approach. Journal of Computational Biol-

ogy, 7(1–2):215–231.

Rom

an-Rold

an, R., Bernaola-Galv

an, P., and Oliver, J. L.

(1998). Sequence compositional complexity of dna

through an entropic segmentation method. Physical

Review Letters, 80(6):1344–1347.

Santhanam, M. S. and Patra, P. K. (2001). Statistics of atmo-

spheric correlations. Physical Review E, 64:016102.

Taylor, J. B. (2009). The ﬁnancial crisis and the policy re-

sponses: An empirical analysis of what went wrong.

NBER Working Paper No. 14631.

oth, B., Lillo, F., and Farmer, J. D. (2010). Segmenta-

tion algorithm for non-stationary compound poisson

processes. The European Physical Journal B - Con-

densed Matter and Complex Systems, 78(2):235–243.

Vaglica, G., Lillo, F., Moro, E., and Mantegna, R. N.

(2008). Scaling laws of strategic behavior and size

heterogeneity in agent dynamics. Physical Review E,

77(3):036110.

Wang, Y., Leung, L. R., McGregor, J. L., Lee, D.-K.,

Wang, W.-C., Ding, Y., and Kimura, F. (2004). Re-

gional climate modeling: Progress, challenges, and

prospects. Journal of the Meteorological Society of

Japan, 82(6):1599–1628.

Wong, J. C., Lian, H., and Cheong, S. A. (2009). Detect-

ing macroeconomic phases in the dow jones industrial

average time series. Physica A, 388(21):4635–4645.

Zhang, Y., Lee, G. H. T., Wong, J. C., Kok, J. L., Prusty,

M., and Cheong, S. A. (2011). Will the us economy

recover in 2010? a minimal spanning tree study. Phys-

ica A, 390(11):2020–2050.

TIME SERIES SEGMENTATION AS A DISCOVERY TOOL - A Case Study of the US and Japanese Financial Markets