MODELLING VITRIFIED GLASS VISCOSITY IN A NUCLEAR

FUEL REPROCESSING PLANT USING NEURAL NETWORKS

Katy Ferguson

, Jie Zhang

, Carl Steele

, Colin Clarke

and Julian Morris

School of Chemical Engineering and Advanced Materials, Newcastle University, NE1 7RU, Newcastle Upon Tyne, U.K.

Sellafield Ltd, Sellafield, Seascale, Cumbria, U.K.

National Nuclear Laboratory, Preston, U.K.

Keywords: Viscosity, Neural networks, Vitrification, Nuclear reprocessing, Modelling, Application.

Abstract This paper presents a study of using neural networks to model the viscosity of simulated vitrified highly

active waste over a range of temperatures and compositions. Vitrification is the process of incorporating the

highly active liquid waste into the glass by chemically changing the structure of the glass for nuclear fuel

reprocessing. A methodology is needed to determine how the viscosity will change as a result of a new feed.

Feed forward neural networks are used to model the viscosity of new product glasses. The results are very

promising, with a Mean Squared Error (MSE) of 1.8x10

-4

on the scaled unseen validation data, highlighting

the high accuracy of the model. Sensitivity analysis of the developed model provides insight on the impact

of composition on viscosity.

1 INTRODUCTION

The wastes from nuclear reactors are radioactive and

need to be treated for long term storage. Vitrification

is one of the nuclear waste treatment processes,

which turns the highly active wastes into a glass

which is much safer for storage. The understanding

of what affects the nuclear waste glass viscosity has

increased due to inactive simulant viscosity tests

carried out at the National Nuclear Laboratory. It is

essential to understand how the viscosity is affected

by the composition using non-active trials.

The experiments provide an insight for plant

engineers/operators on what may happen with

particular feeds. Only a limited number can be

performed due to cost. It is desirable that a model

can be built to predict the viscosity saving the

company a large amount of investment

Developing a detail mechanistic model has been

shown to be difficult, time consuming and effort

demanding. The full mechanism of how various

compositions affect viscosity is not fully understood.

Data based empirical modelling can be a very useful

alternative in this case. Neural networks have been

shown to be capable of approximating any

continuous nonlinear functions (Cybenko, 1989);

(Girosi and Poggio, 1990); (Park and Sandberg,

1991) and have been applied to nonlinear process

modelling (Bhat and McAvoy, 1990); (Bulsari,

1995); (Duchesne et al., 2010); (Narendra and

Parthasarathy, 1990); (Zhang et al., 1998).

This paper presents a study on using neural

networks to model the viscosity of simulated

vitrified highly active waste over a range of

temperatures and compositions. Section 2 gives a

brief description of the processes. Neural network

modelling of glass viscosity is presented in Section

3. The obtained results are discussed in Section 4

and conclusions given in Section 5.

2 PROCESS DESCRIPTIONS

2.1 Waste Vitrification Plant

The Vitrification plant (Figure 1) is responsible for

converting Highly Active Liquor (HAL) into a

durable product glass. HAL, consisting of waste

fission products in nitric acid, and other calcination

additives are fed into a hot revolving furnace. The

liquid is evaporated leaving dry particles.

The particles are dropped into a melter with

Borosilicate glass frit and heated to high

temperatures resulting in a new glass matrix being

322

Ferguson K., Zhang J., Steele C., Clarke C. and Morris J..

MODELLING VITRIFIED GLASS VISCOSITY IN A NUCLEAR FUEL REPROCESSING PLANT USING NEURAL NETWORKS.

DOI: 10.5220/0003654003220325

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 322-325

ISBN: 978-989-8425-84-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

formed, different from waste encapsulating. The

glass is poured into a container. The container is

then cooled, lid welded on, decontaminated,

monitored then taken for long term storage.

2.2 Inactive Laboratory Experiments

Experiments were carried out in order to test many

properties of the glass (Steele et al., 2011.) One

property of the glass produced is its viscosity,

relating to the pour rate, which can be measured on

the active plant.

There are 4 groups of experiments, in total

consisting of 28 compositions. The simulant glasses

were made up in the laboratory with similar

chemical compositions to what is expected. The

viscosity readings were from a high temperature

rotating viscometer. Batches of the glasses were put

into an alumina crucible. The glass was heated to

1200°C and held at this temperature for 45 minutes.

The rotor was lowered 20mm into the glass and

measurements taken every 10 seconds during the

cooling period down to 900°C at a rate of 2°C per

minute. The cleaning process will not be described.

3 VISCOSITY MODELLING

By using the estimated compositions and a range of

temperature, a viscosity curve can be predicted.

Multiple Linear Regression is used to show that the

data is non-linear. Neural Networks will be used to

model viscosity due to the high complexity and time

consuming nature of mechanistic models.

3.1 Multiple Linear Regression

Multiple Linear Regression (MLR) is a linear

technique used to predict (Montgomery, 2006) and

takes the following form:

iMiMiii

exbxbxbby 

,2,21,10

(1)

where b

is the regression coefficient, b

is the

coefficient of the M

predictor, x

i,M

is the M

predictor at time i, e

is the error at time i and y

the value of the variable at time i. This method will

not be explained further, as the MLR approach does

not predict viscosity. Figure 2 shows the relationship

between measured and predicted viscosity with the

line measured viscosity equals predicted viscosity

shown. It shows that the data is highly non-linear

and therefore is not the correct approach to use.

Figure 1: A Waste Vitrification Plant.

3.2 Neural Networks

In this paper, Neural Networks are analysed as a

methodology to model viscosity using composition

and temperature. The most commonly used is the

multi-layer feed forward neural network. Inputs are

presented at the input layer, I

. The data is

propagated through the network through complex

connections. The hidden layer structure defines the

topology of a feed forward network. It is possible to

have more than one hidden layers and is proven to

approximate any continuous non linear function with

sufficient number of hidden neurons (Cybenko,

1989). Single hidden layer neural networks are used

in nonlinear system modelling (Pham and Liu, 1995;

Lennox et al., 1998).

Each interconnection has a scalar weight, w

which modifies the signal strength. The neurons

within the hidden layer: sum the weighted inputs and

pass through a non-linear activation function as well

as a bias, b. The output of a hidden neuron, O known

as the sigmoidal neuron activation function and its

output is in the range (0, 1).

SbwI







()

(2)





1exp( )

(3)

Figure 2: Measured against predicted viscosity using

MLR.

MODELLING VITRIFIED GLASS VISCOSITY IN A NUCLEAR FUEL REPROCESSING PLANT USING NEURAL

NETWORKS

323

Table 1: Mean squared errors (scaled) of neural network

model predictions.

Data set MSE

Training 1.0879e-4

Testing 2.9992e-4

Validation 1.8430e-4

Network weights are such trained so that the sum

of squared network prediction errors, Eq(4) is

minimised.

yt yt







(



() ())

(4)

where N is the number of training data points,



the network prediction, y in the target value, and t is

an index of the training data. The most commonly

used network training method is the back

propagation training method (Rumelhart et al.,

1986), where network weights are adjusted as

follows.

Wk Wk

() ()

()

 1





(5)

W(k+1) = W(k) + W(k+1)

(6)

W(k) and W(k) are the weight and weight

adaptation at the training step k respectively,  is the

momentum coefficient, and  is the learning rate.

Training can be terminated when the error gradient

is less than a pre-specified value, e.g. 10

-6

or by a

cross validation based stopping criterion. When

using the latter, data for building a neural network

model is divided into a training data set and a testing

data set. The network prediction error on the testing

data is continuously monitored and terminated when

the testing error stops decreasing.

3.3 Neural Networks Viscosity

Prediction

The glass contains 24 different components, C

and

will be in terms of number of Moles. The

temperature, T, ranges from 1200 to 900°C in the

experiment. The output is the viscosity, V which is

of the form:

V = f(T, C

,...,C

) (7)

The data set was split up into training (20%), testing

(40%), and validation data sets (40%). The data

were trained using the Levenberg-Marquardt

optimisation algorithm (Marquardt, 1963) with

regularisation and early stopping. The purpose of

regularisation and early stopping is to avoid over-

fitting noise in the training data. A regularisation

term is added to the training objective function to

penalise large network weights. A feed forward

neural network with 25 inputs, 7 hidden nodes in a

single hidden layer and 1 output was created.

4 RESULTS

4.1 Neural Network Predictions

The model proved to be successful at modelling

viscosity using composition and temperature. Figure

3 shows a plot of temperature against viscosity. The

blue line represents the true values while the red

lines represents the model predictions. The error

appears to be small. Table 1 gives the mean squared

errors (MSE) of the neural network model

predictions on the training, testing, and unseen

validation data sets.

The MSE given in Table 1 are for scaled data,

i.e. scaled to zero mean and unit variance. The very

low MSE values in Table 1 indicate that the

developed neural network model is very accurate.

4.2 Sensitivity Analysis of the Neural

Network Model

Initial work has been carried out to investigate the

model sensitivity to various model inputs. This study

uses a numerical method where a small perturbation

is added to one of the inputs while keeping other

inputs unchanged. The ratio between the resulting

change in model output and the applied model input

is the model sensitivity to that input:



ySensitivit

(8)

Figure 3: Graph showing actual (blue) and predicted

viscosity curve over time (red).

NCTA 2011 - International Conference on Neural Computation Theory and Applications

324

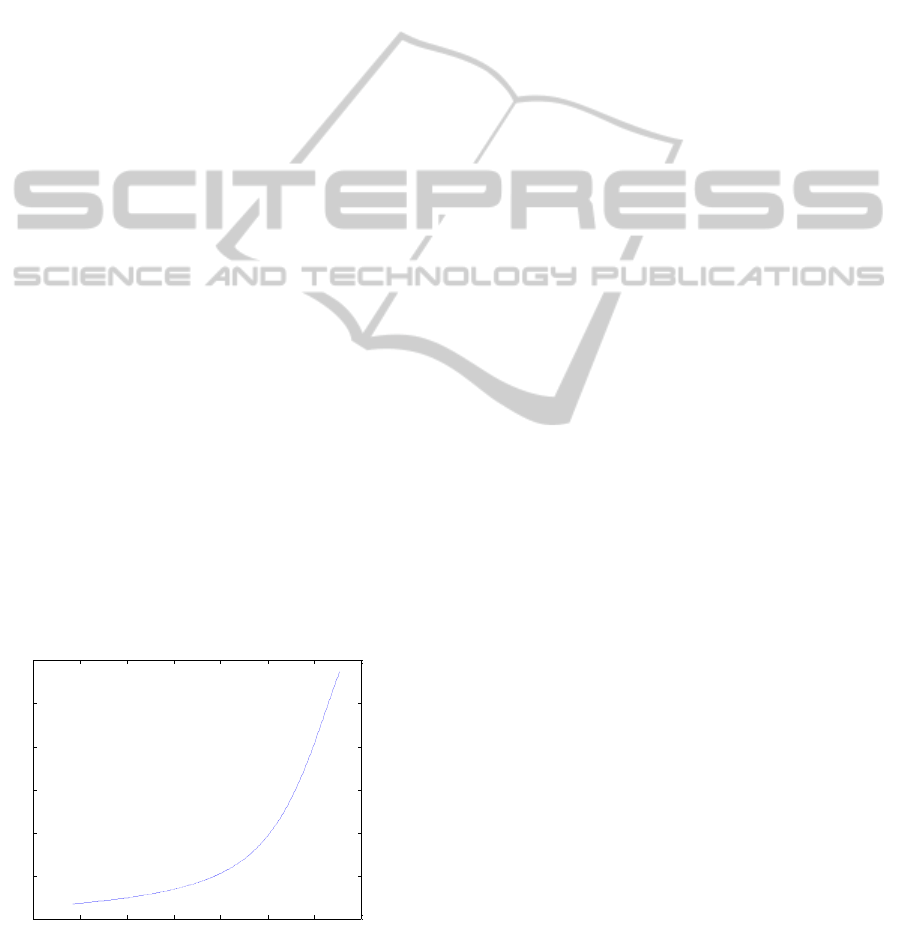
The sensitivity changes, due to the non-linearity.

If it changes considerably with only small changes

in the component, then this suggests that the

component significantly affects the viscosity.

Figure 4 shows the sensitivity curve when a

variables is perturbed. Above 0.035Moles, there is

an increase in viscosity, highlighting that variable

has a big effect on viscosity.

5 CONCLUSIONS

This paper has used a well proven technique,

multilayer feed forward neural networks, to predict

the viscosity over a range of temperatures and

different glass compositions. The prediction error

(MSE) of the model for this range of feed was found

to be 1.84x10

-4

for the scaled validation data set

which highlights the model’s accuracy at predicting

viscosity.

The model is only valid over a certain range for

each variable, but in future work the model will be

adapted for further different compositions and feeds.

The work carried out so far has provided

encouraging predictions for a larger range of

compositions. This will be developed into a user tool

for a greater understanding of how the composition

will affect the viscosity.

ACKNOWLEDGEMENTS

The author would like to thank Northern way and

Technology Strategy Board for part funding the

Knowledge Transfer Partnership. The author would

also like to thank Barbara Dunnett, National Nuclear

Laboratory for the initial guidance on this study.

0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045

Figure 4: Sensitivity graph for variable 25.

REFERENCES

Bhat, N. V. and T. J. McAvoy (1990) “Use of neural nets

for dynamical modelling and control of chemical

process systems”, Computers & Chemical

Engineering, 14, 573-583.

Bishop, C. (1995) Neural Networks for Pattern

Recognition. Oxford University Press: Oxford.

Bulsari, A. B., (Ed), (1995) Computer-Aided Chemical

Engineering, Vol.6, Neural Networks for Chemical

Engineers, Elsevier: Amsterdam.

Cybenko, G. (1989) “Approximation by superposition of a

sigmoidal function”, Math. Control Signal Systems, 2,

303-314.

Duchesne, M. A., Macchi, A., Lu, D.Y., Hughes, R. W.,

McCalden, D., J. Anthony, E. J., (2010) Artificial

neural network model to predict slag viscosity over a

broad range of temperatures and slag compositions -

Fuel Processing Technology, Volume 91, Issue 8,

Pages 831-836

Girosi, F. and T. Poggio (1990) “Networks and the best

approximation property”, Biological Cybernetics, 63,

169-179.

Lennox, B., Rutherford, P., Montague, G. A., Haughin, C.,

(1998) Case study investigating the application of

neural networks for process modelling and condition

monitoring – Computers & Chemical Enginerring,

Volume 22, Issue 11, Pages 1573-1579

Marquardt, D. (1963) “An algorithm for least squares

estimation of nonlinear parameters”, SIAM J. Appl.

Math., 11, 431-441.

Montgomery, D. C., Peck, E. A., Vining, G. G.,

Introduction to Linear Regression Analysis, Wiley

Series in Probability and Statistics

Narendra, K. S. and K., Parthasarathy (1990)

“Identification and control of dynamical systems using

neural networks”, IEEE Transactions on Neural

Networks, 1, 4-27.

Park, J. and I. W. Sandberg (1991) “Universal

approximation using radial basis function networks”,

Neural Computation, 3, 246-257.

Pham, D. T., Liu, X., (1995) Neural Networks for

Identification, Prediction and Control. Springer-Verlag

London Limited. 4th edition

Rumelhart, D. E., G. E. Hinton, and R. J. Williams,

“Learning internal representations by error

propagation”, in Parallel Distributed Processing,

(Eds) D. E. Rumelhart and J. L. McClelland, MIT

Press, 1986.

Steele, C. J., Dunnet, B., Riley, A. D., Ferguson, K.,

Gribble, N., Short, R., (2011) Viscosity of simulated

nuclear waste vitrified product International

Conference on the Chemistry of Glasses and Glass-

Forming Melts, To be published

Zhang, J., Morris, A. J., Martin, E. B., Kiparissides, C.,

(1998) Prediction of polymer quality in batch

polymerisation reactors using robust neural networks

Chemical Engineering Journal 69, Pages 135-143

MODELLING VITRIFIED GLASS VISCOSITY IN A NUCLEAR FUEL REPROCESSING PLANT USING NEURAL

NETWORKS

325