EXPERIMENTAL COMPARISON OF SELECTED TYPES

OF PARALLEL EVOLUTIONARY ALGORITHMS

Ivan Sekaj, Marek Linder and Daniel Pernecký

Institute of Control and Industrial Informatics, Faculty of Electrical Engineering and Information Technology

Slovak University of Technology, Ilkovičova 3, 812 19, Bratislava, Slovak Republic

Keywords: Evolutionary Algorithm, Genetic Algorithm, Parallelisation, Architecture, Migration, Overlapping,

Experimental Comparison.

Abstract: Parallel evolutionary algorithms are able to improve the performance of simple evolutionary algorithms

which use a single population. Their characteristics and performance depend on their architectures and other

factors and parameters. In our contribution we present some viewpoints of classification and we

demonstrate experimentally the influence of selected factors such as architecture type, migration topology,

migration period, number of migrants, numbers of subpopulations, subpopulation size and others on the

performance of these algorithms. This experimental study should help to generalise the properties and

behaviour of various types of parallel evolutionary algorithms and help to design algorithms for solving

hard search/optimisation problems like modelling of bio-medicine processes, optimisation of

pharmaceutical dosing, optimisation of large technological and construction tasks etc.

1 INTRODUCTION

Parallel evolutionary algorithms (PEA) or parallel

genetic algorithms (PGA) are evolutionary

algorithms, which consist at least of two levels of

parallelisation. The first level contain most types of

evolutionary algorithms thanks their population

based nature. Each individual represents a trajectory

in the search space. The main drawback of the

simple or single-population algorithms is the high

computation effort or time needed to find the

solution. The next drawback is that simple

evolutionary algorithms are often unable to avoid the

premature convergence, which is the stagnation in

the local optimum. To prevent these drawbacks a

next level of parallelisation using multiple

populations can be used.

Several authors used various types of PEA and

several authors published various classifications of

PEA or PGA (Alba, 2002, Cantú-Paz, 1995,

Nowostawski, 1999 and others). The PEA, aside

from the number of computation units used

(processors, computers), bring also other advantages

in comparison to simple (single-population)

evolutionary algorithms (SEA) or simple genetic

algorithms (SGA). These advantages are multi-

parallel search in a large, multidimensional search

space, higher diversity of the population, better

algorithm control possibilities, higher computation

power, etc. If we are able to design efficient

architectures of PEA and to find their good

parameters, the PEA will reach better solutions,

avoid premature convergence and reduce time,

which is needed to find the solution in comparison to

SEA. Additionally, if using multiple computation

units the computation power is growing sub linearly.

All together, PEA result in a significant performance

increase.

In this contribution some viewpoints of PEA

classification are described. But the goal of this

paper is an experimental comparison of selected

PGA representatives and analysis of the influence of

selected PEA parameters on their performance. Our

attention was focused to island-based migration-type

PGA, island-based overlapping-type PGA and

cellular PGA. We analysed the influence of PGA

architecture, migration topology, migration period,

number of migrants, number of subpopulations,

subpopulation size and some other factors on the

performance.

2 CLASSIFICATION OF PEA

Let us consider following viewpoints of PEA

classification. The first is the number of computation

296

Sekaj I., Linder M. and Pernecký D..

EXPERIMENTAL COMPARISON OF SELECTED TYPES OF PARALLEL EVOLUTIONARY ALGORITHMS.

DOI: 10.5220/0003655402960302

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 296-302

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

units used, the second is the granularity or the

number of subpopulations and their size and the

third viewpoint is the type of information exchange

between subpopulations of the PEA.

2.1 Number of Computation Units

The first question is how much computation units

are used for the PEA realisation. This is a technical

aspect, which influences computation time, but not

the algorithm as such or the number of the total

fitness function evaluations of the entire PEA

needed for finding a good result. Using N-

computation units (processors, computers) we are

able to speed up the computation power nearly N-

times. The use of multiprocessor configurations

distributes the computation load to more processing

nodes. The simplest computational topology uses

only a single population and the algorithm manager

distributes the fitness function evaluation (or

sometimes also the crossover and mutation) to other

free processors. Such topology is called global or

master-slave. The only communication is the request

for the fitness calculation in one direction and than

the computed fitness value in the other direction.

This topology can by an extensive way save

computation time, but it is not able to decrease the

number of fitness function evaluations.

2.2 Granularity of the PEA

The most obvious viewpoint of PEA (PGA)

classification is the PEA granularity which divide

PEA to coarse-grained and fine-grained ones

(Cantú-Paz, 1995).

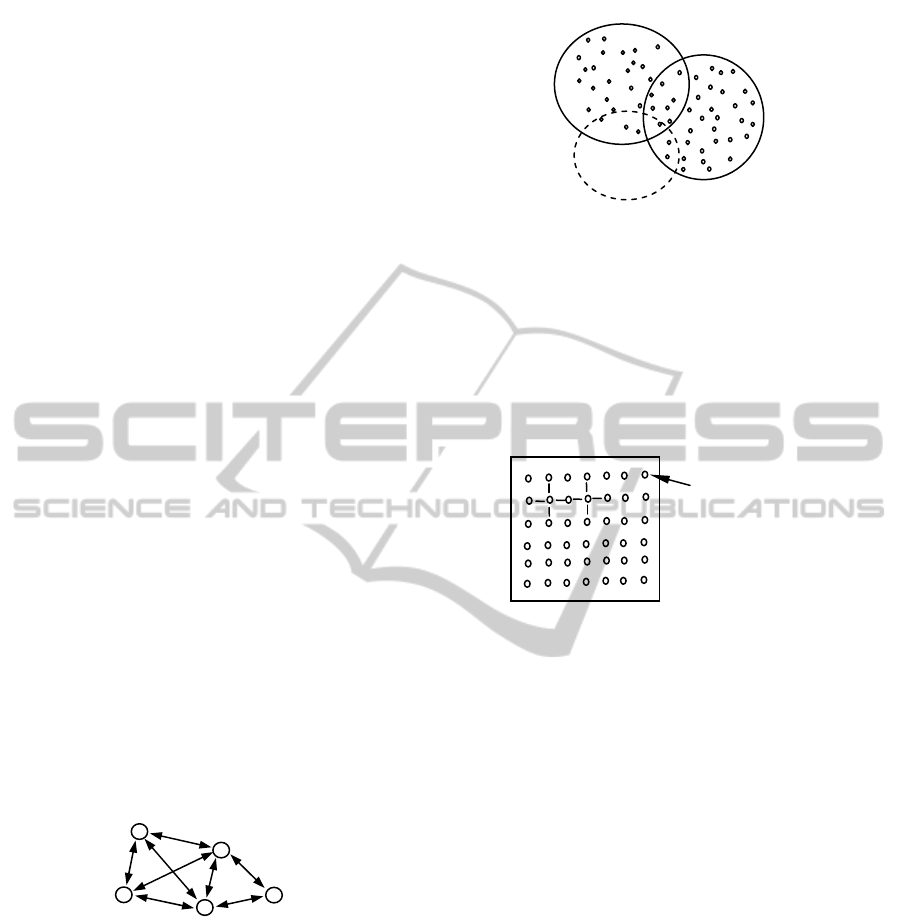
Figure 1: Migration-based coarse-grained PEA.

Coarse-grained PEA consist of relatively small

number of relatively large subpopulations (islands)

(Fig.1, Fig.2). The use of coarse-grained PEA

topologies is advantageous when information

combination of individuals from partially isolated

subpopulations can produce new perspective search

directions or even solutions. Many authors have

presented coarse-gained PGA or island models in

literature e.g. (Lin, 1994, Whitley, 1999, Cantú-Paz,

1999, Skolicki, 2005) and others.

In case of fine-grained PGA many islands with a

small number of individuals are considered. The

Figure 2: Overlapping-based coarse-grained PEA.

outermost but also the most obvious case is when

each island is represented only by a single

individual. Such topology is called also cellular

(Fig.3) (Giacobini, 2005 and others).

The hybrid topologies are the last case of PEA,

which represent various combinations of fine- and

coarse-grained PEA.

Figure 3: Fine-grained cellular PEA.

2.3 Information Exchange in PGA

The last viewpoint of PGA classification discussed

is the information exchange between the

subpopulations. Here let us distinguish migration,

individual sharing and diffusion. The islands in the

coarse-grained PEA interchange the genetic

information either using the migration operator or

sharing some individuals in overlapping areas of

more subpopulations. Migration is performed by

copying of selected individuals from the source

island to the target island according to defined

migration connections (for example as described in

Fig.1). The migration is performed in defined

periodic time intervals or non-periodically when

some predefined conditions are fulfilled. The correct

selection of migration periods should ensure that

each island has sufficient time for isolated evolution

of their individuals and for producing perspective

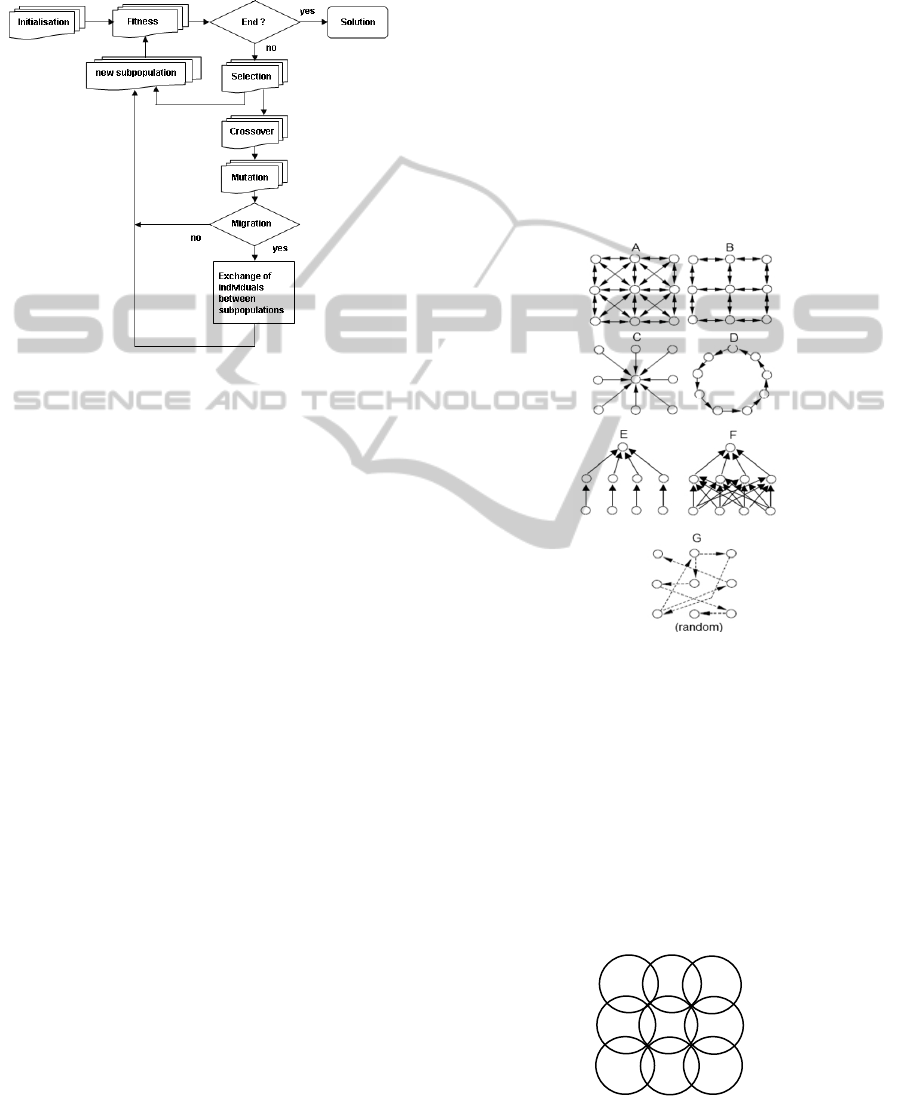
genetic information. Block scheme of such

algorithm is in Fig.4. In the overlapping topology,

selected number of individuals belongs to more

subpopulations; they can be selected as parents and

crossed over with individuals of other

subpopulations (Fig.2). Finally, in the cellular fine-

grained PEA the genetic information is exchanged

ulation

ulation B

ulation

single

individual

EXPERIMENTAL COMPARISON OF SELECTED TYPES OF PARALLEL EVOLUTIONARY ALGORITHMS

297

due to crossover of each individual of the population

with a selected neighbour. The individuals are

geometrically organised in a 2-D or 3-D grid. The

information motion here imitates diffusion.

Figure 4: Block scheme of a migration-based PEA with

multiple subpopulations and migrations between them.

3 USED PGA CONFIGURATIONS

In our experimental analysis three types of PGA

topology have been considered: 1. migration-type

coarse-grained, 2. overlapping-type coarse-grained

and 3. cellular fine-grained. The influence of

selected parameters have been analysed and the

performance of selected PGA configurations have

been compared on the example of minimisation of

the Eggholder function. Note, that during this project

other test function has been tested and a very large

number of experiments was performed.

3.1 Coarse-grained PGA with

Migration

We have used various migration-based PGA

topologies with communication between islands

according to Fig.5 A-G (Sekaj, 2004, Sekaj, 2007).

Each arrow represents a migration direction. When

not explicitly indicated, nine islands were used, each

island consists of 64 individuals and the number of

all individuals in the PGA was 9x64=576. The

following genetic algorithm is running in each

island:

1. Population initialisation (by random) and fitness

calculation.

2. Selection of 4 the best individuals, which are

without any change copied into the new population.

Random selection of a group of 20 individuals,

which are copied without any change into the new

population. Selection of 40 parents using the

tournament selection method.

3. Mutation (rate=0.1) and crossover (rate =0.7) of

parents.

4. Completion of the new population.

5. Fitness calculation.

6. Test of terminating condition, if not fulfilled, then

jump to the Step 2.

The best-random migration policy is used, that is the

best individual from the source island is copied and

it replaces a randomly selected individual in the

target island.

Figure 5: Coarse-grained migration-based PGA topologies

used in our experiments.

3.2 Coarse-grained PGA with

Overlapping areas

This architecture contains overlapping areas where

some individuals belong to more subpopulations and

the information interchange between them is

provided only by crossover (Fig.6). No migration

between islands is provided. However, the

evolutionary algorithm used is the same as in the

previous architecture.

Figure 6: Coarse-grained overlapping-based PGA

topology.

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

298

3.3 Fine-grained PGA

In the considered fine-grained cellular topologies

each node represents a single individual (Sekaj,

2009).

There are 24 rows and 24 columns, together

576 individuals (Fig.7). Two types of the fine-

grained PGA algorithms have been considered. In

each generation we selected one neighbour of 4 or 8

possible neighbour candidates (Fig.7 left and right,

respectively) for each original individual of the

population using tournament selection. These two

individuals are crossed over and two new children

are produced. If one of the two children is better

than the original individual, it replaces it. But the

population is updated (the old individuals are

replaced) as late as the last individual of the PGA is

crossed over. Two alternatives were used for

mutation. In the first case the crossed over children

are mutated and then the best individual is chosen to

replace the original individual. In the second case all

individuals are crossed over, replaced and then the

entire population is mutated with the mutation rate

0.1.

Figure 7: Neighbour selection in cellular PGA topologies.

Each island is a single individual.

4 EXPERIMENTAL RESULTS

4.1 Test Function

For all experiments the Eggholder function of 10

variables has been used. It is in form

(1)

-500 ≤ x

≤500

The position of the global optimum is unknown.

Graph of this function with two variables is in Fig.8

Figure 8: Graph of the Eggholder function with 2

variables.

4.2 Experimental Results

The goal was to perform an experimental analysis of

the above described PGA architectures and to find

the important factors, which have positive influence

on their performance. We have analysed and

compared the influence of the PGA type and its

topology, migration period length, number of

individuals migrated, number of islands and

population size on the convergence rate. Each graph

in the depicted figures represents the mean value of

30 runs of the corresponding PGA.

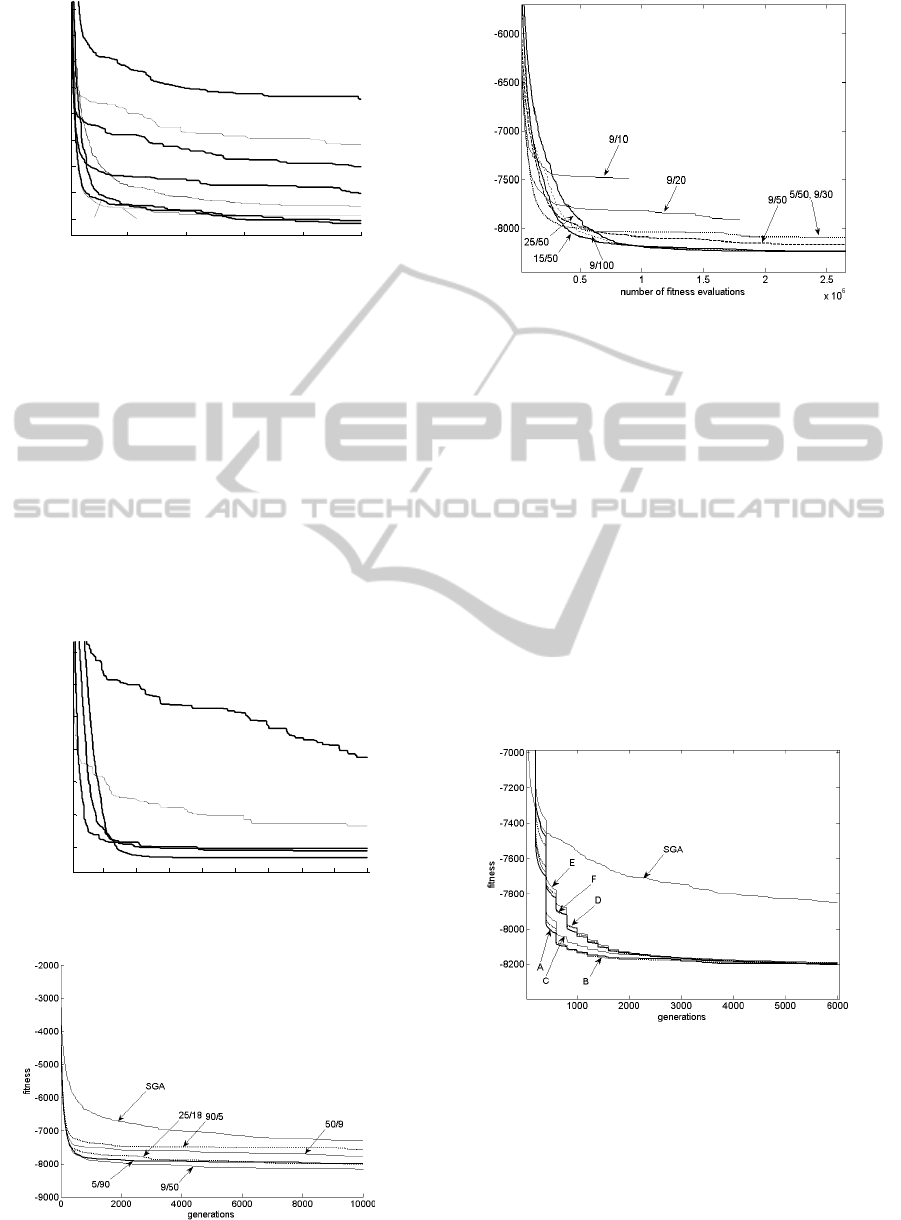
In the first experiment the topology B with 9

islands (Fig.5B) is considered. The influence of

changing migration period is analyzed (Fig.9).

Migration period from 1 to 100 generations has been

compared. The best performance was obtained with

migration period between 20 and 100 generation.

When shorter migration periods, from 1 to 10

generation, were used the PGA starts to behave

similar as the single population GA (SGA) because

of frequent information exchange between the

islands. Such results were worst than the PGA

without migration (marked - No migration). In the

SGA and in PGA with intensive migration the

algorithm is predisposed to premature convergence.

This is because the currently best individuals which

direct to local optima, can influence the entire

population i.e. influence other subpopulations to

premature convergence before they are able to

evolve perspective genes or building blocs

respectively.

EXPERIMENTAL COMPARISON OF SELECTED TYPES OF PARALLEL EVOLUTIONARY ALGORITHMS

299

1000 2000 3000 4000 5000

-8000

-7800

-7600

-7400

-7200

-7000

-6800

-6600

-6400

generation

Fitness

SGA

T=1

T=5

T=10

No migration

T=100

T=20

T=50

Type B, Changing migration period

Test function 1

Figure 9: The influence of changing migration period.

Next, the influence of changing the number of

islands is compared. Fig.10 depicts results reached

with 5 to 25 islands. Number of individuals in each

island is 50. The number of all individuals in the

PGA is not constant. It is Nx50, where N is the

number of islands. For objective comparison the

number of fitness function evaluations instead of

number of generations is used on the horizontal

axes. The best result was obtained with 25 islands.

The next experiments (Fig.11 and Fig.12) show that

for the Eggholder function with 10 variables the

optimal number of islands is between 9 and 25 with

subpopulation size from 50 to 100 individuals.

1 2 3 4 5 6 7 8 9

x 10

-8200

-8000

-7800

-7600

-7400

-7200

-7000

No. of fitness evaluation

Fitness

SGA

Type B, Changing number of subpopulations

Test function 1

Figure 10: The influence of changing number of islands.

Figure 11: Number of islands / population size.

Figure 12: Number of islands / population size.

In Fig.13 various topologies of migration

connections (according Fig.5) have been compared.

In case of the Eggholder function the topologies A,

B and C shows faster convergence rate. However, in

general we assume that the migration connection

topology has not a significant influence on the PGA

performance. Note, that this can change, if we

consider PGA with "heterogeneous" structure i.e.

when various parameters of GA are used in various

islands or regions of the PGA. In such a way it is

possible to control the selective pressure and

population diversity in the PGA (Sekaj, 2004, Sekaj,

2007). However, this was out of the scope of this

paper. In this paper a "homogeneous" PGA structure

is considered, where each subpopulation has the

same genetic algorithm and its parameters.

Figure 13: Various topologies of migration-based PGA.

Higher influence than the migration topology has the

migration period, number of islands and the

subpopulation size. In Fig.14 comparison of

changing migration periods vs. changing number of

migrants is shown. Here the random migration

topology G (Fig.5) has been used. In all cases

similar (or even equal) numbers of migrants in a

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

300

longer time interval were exchanged. The best

performance has been obtained with the migration

period between 20 and 100 generations.

Lower or higher values of migration periods results

in worst performance. Each subpopulation needs

time between the migrations for their isolated

evolution to produce perspective genes or building

blocs, respectively. On the other hand, the number of

migrants hasn't a significant influence on the

performance ( Fig.15).

The next important factor is the population size.

In Fig.11 various configurations (number of islands /

population size) are compared. In each case the

number of individuals in the entire PGA was 450.

The best performance results from the configuration

9/50, which has a sufficient number of islands as

well as sufficient subpopulation size. In Fig.12 the

same factors are considered, but the numbers of

individuals in the entire PGA are not equal.

Therefore, on the horizontal axes the number of

fitness evaluations instead of the number of

generations is used. The best performance was

obtained with the configurations 15/50, 25/50 and

9/100 where sufficient number of islands and

sufficient subpopulation sizes ensures satisfactory

conditions, sufficient diversity and relative

independence of particular subpopulations.

Figure 14: Migration period / number of migrants.

Figure 15: Changing number of migrants, migration period

is 100 generations.

In Fig.16 the results of the overlapping-based PGA

are compared. We consider the architecture

according Fig.6 and Fig.7 with 9 overlapping

subpopulations. The number of individuals in the

overlapping areas has been changed from 2 to 10

and 16 individuals. The best performance has been

obtained with 10 shared individuals between each

two subpopulations.

Figure 16: Overlapping PGA, various numbers of shared

individuals.

The last mentioned PGA type is the fine-grained or

cellular architecture. Four variants of this algorithm

are compared in Fig.17. The algorithms are

described in the part 3.3. The first two types (1 and

2) perform mutation at the end of the new generation

calculation, when all individuals of the population

are already crossed over with selected neighbours

and replaced by the best offspring. Type 1 selects

the partner for crossing over from 8 neighbours

(Fig.7 left) and type 2 from 4 neighbours (Fig.7

right). Types 3 and 4 perform the mutation after

crossover of both parents. Then the best mutated

individual replaces the original individual. Type 3

selects the partner for crossover from 8 neighbours

and the type 4 from 4 neighbours.

Figure 17: Various types of cellular PGA.

EXPERIMENTAL COMPARISON OF SELECTED TYPES OF PARALLEL EVOLUTIONARY ALGORITHMS

301

The last figure (Fig.18) depicts the comparison of

the best representatives of all PGA architectures.

The fastest convergence in case of the Eggholder

function has been achieved by the fine-grained

(cellular) PGA.

Figure 18: Comparison of various PGA types: Coarse-

grained migration-based PGA (C-M), Coarse-grained

overlapping-based PGA (C-O), Fine-grained PGA (F).

5 CONCLUSIONS

Selected types of parallel genetic algorithms have

been experimentally compared and the influence of

some of their parameters analyzed. We have

considered various architectures, various topologies

of migration connections, influence of changing

migration period, population size and number of

islands. In our experiments using the Eggholder

function the fine-grained PGA performance

outperforms the coarse-grained PGA. However, the

performance of all PGA types depends on their

parameters as well as on the problem to be solved.

In our comparison in each island of the PGA the

genetic algorithm with equal parameters has been

considered. Such "homogenous" algorithms have the

same diversity and selection pressure in all

subpopulations. Based on our experiments for such

type of PGA (PEA) we can make following

conclusions. Changing of migration topology has a

small influence on the PGA performance. The main

influence on the performance has the migration

period, subpopulation size and number of islands.

These factors affect the ability of all subpopulations

of the PGA to evolve perspective genes and building

blocs and effectively to explore the search space.

For each problem solved it is important to find a

balance between the "independence" of each

subpopulation for their evolution and diversity in

each subpopulation on the one side and the

communication and exchange of perspective genetic

information between subpopulations or individuals

on the other side.

The presented experimental study is a part of a

project, which should help to generalise the

properties and behaviour of various types of

parallel evolutionary algorithms and help to design

algorithms for solving hard search/optimisation

problems like modelling of bio-medicine processes,

optimisation of large technological and construction

tasks, solving of economical and financial problems

etc.

ACKNOWLEDGEMENTS

This work was supported by the Slovak Research

and Development Agency under the contract No.

APVV-0523-10.

REFERENCES

Alba E., Tomassini M., 2002. Parallelism and

Evolutionary Algorithms. In IEEE Trans. on

Evolutionary Computation, Vol. 6, NO.5.

Cantú-Paz E., 1995. A Summary of Research on Parallel

Genetic Algorithms. In IlliGAL Report No. 95007.

University of Illinois at Urbana-Champaign.

Cantú-Paz E., 1999. Migration Policies, Selection

Pressure, and Parallel Evolutionary Algorithms. In

IlliGAL Report 99015, University of Illinois at

Urbana-Champaign.

Giacobini M., Tomassini M., Tettamanzi A.G.B., Alba E.,

2005. Selection intensity in cellular evolutionary

algorithms for regular lattices. In IEEE Transactions

on Evolutionary Computation.

Lin S. Ch., Punch W., Goodman E., 1994. Coarse-grain

parallel genetic algorithms: Categorization and new

approach. In IEEE Symposium on Parallel and

Distributed Processing.

Nowostawski M., Poli R., 1999. Parallel Genetic

Algorithm Taxonomy. In KES’99.

Sekaj I., 2004. Robust Parallel Genetic Algorithms with

Re-Initialisation. In PPSN VIII, September 18-22,

Birmingham.

Sekaj I., Perkacz J., 2007. Some Aspects of Parallel

Genetic Algorithms with Population Re-initialization.

In CEC, Singapore.

Sekaj, I., Oravec, M., 2009. Selected Population

Characteristics of Fine-grained Parallel Genetic

Algorithms with Re-initialisation. In Proceedings of

the GEC 2009, Shanghai.

Skolicki Z., DeJong K., 2005. The inﬂuence of migration

sizes and intervals on island models. In GECCO,

Washington, USA.

Whitley D., Rana S., Heckendorn R. B.,1999. The island

model genetic algorithm: On separability, population

size and convergence. In Journal of Computing and

Information Technology, 7(1), pp.33-47.

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

302