
NEURAL NETWORKS COMPUTING THE DUNGEAN SEMANTICS
OF ARGUMENTATION
Yoshiaki Gotou
Graduate School of Science and Technology, Niigata University, Niigata, Japan
Takeshi Hagiwara, Hajime Sawamura
Institute of Science and Technology, Niigata University, Niigata, Japan
Keywords:
Argumentation, Semantics, Neural network.
Abstract:
Argumentation is a leading principle foundationally and functionally for agent-oriented computing where rea-
soning accompanied by communication plays as essential role in agent interaction. In the work of (Makiguchi
and Sawamura, 2007a) (Makiguchi and Sawamura, 2007b), they constructed a simple but versatile neural
network for the grounded semantics (the least fixed point semantics) in the Dung’s abstract argumentation
framework (Dung, 1995). This paper further develop its theory so that it can decide which argumentation se-
mantics (admissible, stable, complete semantics) a given set of arguments falls into. In doing so, we construct
a more simple but versatile neural network that can compute all extensions of the argumentation semantics.
The result leads to a neural-symbolic system for argumentation.
1 INTRODUCTION
Much attention and effort have been devoted to the
symbolic argumentation so far (Ches˜nevar et al.,
2000)(Prakken and Vreeswijk, 2002)(Besnard and
Doutre, 2004)(Rahwan and Simari, 2009), and its ap-
plication to agent-oriented computing. Argumenta-
tion can be a leading principle both foundationally
and functionally for agent-oriented computing where
reasoning accompanied by communication plays an
essential role in agent interaction. Dung’s abstract
argumentation framework and argumentation seman-
tics (Dung, 1995) have been one of the most in-
fluential works in the area and community of com-
putational argumentation as well as logic program-
ming and non-monotonic reasoning. A. Garcez et al.
proposed a novel approach to argumentation, called
the neural network argumentation (Garcez et al.,
2009). In the papers (Makiguchi and Sawamura,
2007a)(Makiguchi and Sawamura, 2007b), they dra-
matically developed their initial ideas on the neu-
ral network argumentation to various directions in a
more mathematically convincing manner. In this pa-
per, we further develop its theory so that it can de-
cide which argumentation semantics (admissible, sta-
ble, complete semantics) a given set of arguments
falls into. For this purpose, we will construct a
more simple but versatile neural network that can
compute all extensions of the argumentation seman-
tics (Dung, 1995)(Caminada, 2006), and lead to a
neural-symbolic system for argumentation (Levine
and Aparicio, 1994)(Garcez et al., 2009).
The paper is organized as follows. In Section 2,
we recall what Dung’s influential work on the abstract
argumentation framework and argumentation seman-
tics is like, for the preparation of the succeeding sec-
tions. In Section 3, we introduce a 4-layer neural net-
work and a translation of a given abstract argumen-
tation framework to it, and a calculation of the argu-
mentation semantics with it. In Section 4, we describe
an implementation of our neural argumentation with
illustrating examples. Final section include previous
work,future work, and concluding remarks.
2 ARGUMENTATION
SEMANTICS
Argumentation semantics is an important subject
since it tells us what correct or justified arguments are.
However, there can be plural semantics for argumen-
5
Goto Y., Hagiwara T. and Sawamura H..
NEURAL NETWORKS COMPUTING THE DUNGEAN SEMANTICS OF ARGUMENTATION.
DOI: 10.5220/0003656600050014
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 5-14
ISBN: 978-989-8425-84-3
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

tation, mainly derived from the nature of argumenta-
tion. We introduce the most basic and influential defi-
nitions for argumentation semantics which originated
with (Dung, 1995).
2.1 Argumentation Framework
The argumentation semantics begins with the defi-
nition of (abstract) argumentation framework (Dung,
1995). We are then concerned with calculating all ex-
tensions of the semantics for an argumentation frame-
work. Then we assume the argumentation framework
to be finite.
Definition 1 (Argumentation Framework) (Dung,
1995). An argumentation framework (A F ) is a pair
hAR, attacksi where AR is a finite set of arguments,
and attacks is a binary relation over AR (in symbols,
attacks ⊆ AR ×AR).
Each element A ∈ AR is called argument and
(A,B) means argument A attacks argument B. An ar-
gumentation framework can be represented as a di-
rected graph where the arguments are represented as
nodes and the attack relation is represented as arrows.
In this paper, we don’t consider the internal structure
of each of the arguments. For this reason, we don’t
refer to the structure of attack relations.
Example 1 ( Ralph goes Fishing) (Caminada,
2008). Consider the following arguments:
Argument A. Ralph goes fishing because it is Sun-
day.
Argument B. Ralph does not go fishing because it is
Mother’s day, so he visits his parents.
Argument C. Ralph cannot visit his parents, because
it is a leap year, so they are on vacation.
Three arguments are represented as A, B and C. In
this case, we can see (B, A) as an attack relation be-
cause B says that Ralph does not go fishing against A.
Similarly to (B, A) we can see (C, B) as an attack re-
lation. An example of an argument framework of the
argumentation is given in Figure 1.
B CA
Figure 1: A F =h {A, B,C}, {(B, A), (C, B)} i.
2.2 Dung’s Argumentation Semantics
The following definitions are basic notions and used
in defining the argumentation semantics.
Definition 2. Let (AR,attacks) be an argumentation
framework,A,B∈AR and S⊆ AR.
attacks(A, B) iff (A, B) ∈ attacks.
S
+
= {A ∈ AR|attacks(S, A)} .
attacks(S, A) iff ∃C ∈ S(attacks(C, A)).
In the definition above, S
+
means a set of argu-
ments attacked by the arguments belonging to the S.
Definition 3 (Conflict-free (Dung, 1995)). Let (AR,
attacks) be an argumentation framework and let S ⊆
AR. S is said to be conflict-free iff S ∩ S
+
=
/
0.
In example 1, according to the definition 3, {A,C}
is conflict-free but {A,B}is not conflict-free. The no-
tion of conflict-free means that there don’t exsit any
attack relations each other.
The notion of defend is a core of argumentation
semantics and defined as follows.
Definition 4 (Defend (Dung, 1995)). Let (AR,atta-
cks) be an argumentation framework, A ∈ AR and
S ⊆ AR. S is said to defend A (in symbols, de-
fends(S,A)) iff ∀B∈AR(attacks(B,A)→attacks(S,B)).
In example 1, according to the definition 4,
defends({C}, A) holds. And note that there are at
least two attack relations when defends(S, A) holds
(except S=
/
0). For example, (C,B) and (B,A) exist in
example 1. For this reason, the neural network to be
proposed in section 3 needs input, first hidden, and
second hidden layer. So we can obtain two connec-
tions from input layer to second hidden layer. At the
same time the neural net work consisted of the 3-layer
implements the notion of de fend.
The following characteristic function F is useful
for understanding the argumentation semantics and
defined by the notion of defend.
Definition 5 (Characteristic Function F) (Dung,
1995). Let (AR,attacks) be an argumentation frame-
work and S ⊆ AR. We introduce a characteristic
function as follows:
• F : 2
AR
→ 2
AR
• F(S) = {A∈AR | defends(S,A)}
With these in mind, we give a series of definitions
for the argumentation semantics.
Definition 6 (Admissible Set (Dung, 1995)). Let
(AR,attacks) be an argumentation framework and S
⊆ AR. S is said to be admissible
iff S is conflict-free and ∀ A ∈ AR ( A ∈ S → de-
fends(S,A) )
iff S is conflict-free and S ⊆ F(S).
NCTA 2011 - International Conference on Neural Computation Theory and Applications
6

According to Definition 6, the empty set is surely
admissible set.
Definition 7 (Preferred Extension (Dung, 1995)).
Let (AR,attacks) be an argumentation framework and
S ⊆ AR. S is said to be a preferred extension iff S is
a maximal (w.r.t set-inclusion) admissible set.
Definition 8 (Complete Extension (Dung, 1995)).
Let (AR,attacks) be an argumentation framework and
S ⊆ AR. S is said to be a complete extension
iff S is conflict-free and ∀ A ∈ AR ( A ∈ S ↔
defends(S,A) )
iff S is conflict-free and S=F(S).
Definition 9 (Stable Extension (Dung, 1995)). Let
(AR,attacks) be an argumentation framework and S
⊆ AR. S is said to be a stable extension
iff S is conflict-free and ∀ A ∈ AR ( A 6∈ S→ at-
tacks(S,A) )
iff S is conflict-free and S∪S
+
=AR.
The definition of the stable extension doesn’t need
the notion of defend. Therefore we need to construct
another layer for the neural network in order to com-
pute the stable extension. In fact, output layer is im-
plememted for it.
Definition 10 (Grounded Extension) (Dung,
1995). Let (AR,attacks) be an argumentation frame-
work. The grounded extension is the minimal fixpoint
of F.
We represent Admissible Set, Preferred Extension,
Complete Extension, Stable Extension and Grounded
Extension as AS, PE, CE, SE and GE respectively.
Example 2 (Argumentation Semantics in A F ).
Let h{A,B,C,D,E},{(A,B),(B,C),(C,D),(D,C),(D,E),
(E,E)}i be an argumentation framework. The A F
represented as a directed graph is given in figure 2.
B DA C E
Figure 2: A F = h{A, B,C, D, E}, {(A,B), (B,C), (C, D), (D,
C), (D, E), (E, E)}i.
All extensions of the argumentation semantics in
A F are calculated as follows:
• AS :
/
0, {A}, {D} , {A,C}, { A, D}
• CE : {A}, {A,C}, {A, D}
• PE : {A,C}, {A, D}
• SE : { A, D}
• GE : {A}
In the next section, we give a neural network
which can computationally accomplish the argumen-
tation semantics described so far.
3 NEURAL NETWORK
CALCULATING DUNG’S
ARGUMENTATION
SEMANTICS
We present how to construct a neural network which
computes the argumentation semantics from A F and
determines it using the constructed neural network.
Once a neural network has been constructed for an ar-
gumentation framework, we can compute its seman-
tics automatically. This means the neural network
incorporates such an apparatus as for computing the
characteristic function (cf. Definition 5).
From this section, we represent a translated neural
network from A F as N and let (AR, attacks) be an
argumentation framework.
3.1 Translation from A F to N
3.1.1 The Number of Attacks
Before the translation algorithm from A F to N , we
introduce the function A which tell us the number of
attacks for each argument. And the values generated
from the function A define the threshold θ
α
k
of the
second hidden neuron α
kh
2
.
Definition 11 (Function A ). We introduce a function
A as follows:
• A :AR → N
• A (X) = |{(Y, X)|Y ∈ AR∧(Y, X) ∈ attacks}|
Example 3. Examples of function A in Figure 2 are
given as follows:
• A (A) = |
/
0| = 0
• A (B) = |{(A, B)}| = 1
• A (C) = |{(B,C)}, {(D,C)}| = 2
• A (D) = |{(C, D)}| = 1
• A (E) = |{(D, E)}, {(E, E)}|= 2
Generally the size of attacks equals the sum
of function A for all arguments. For example 3,
attacks = A (A) + A (B) + A (C) + A (D) + A (E) =
0+1+2+1+ 2= 6. In addition the value of function
NEURAL NETWORKS COMPUTING THE DUNGEAN SEMANTICS OF ARGUMENTATION
7
A (X) means the degree of difficulty of the defend for
the argument X. Therefore if the function A (X) takes
high value, it is difficult to defend the argument X.
3.1.2 Translation Algorithm
This subsubsection is a core part of this paper and
shows the translation algorithm from A F to N . It
is defined as follows:
Step 1 (Input). Given an argumentation framework
hAR, attacksi where AR = {α
1
, α
2
, ..., α
n
}.
Step 2 (Types of Neurons). For each argument α
k
∈AR (1≤k≤n), a neuron is created for each layer
(input layer, first hidden layer, second hidden
layer and output layer) and named as α
kX
(see Ta-
ble 1 about X).
Table 1: Representation rules of neuron.
Layer name of neuron X
Input layer i
First hidden layer h
1
Second hidden layer h
2
Output layer o
Step 3 (Weight). Let a, b be positive real numbers
and satisfy
√
b > a > 0. For each argument α
k
∈
AR (1≤k≤ n), do (i) ∼ (iii).
(i) connect input neuron α
ki
to first hidden neuron
α
kh
1
and set a as the connection weight.
(ii) connect hidden neuron α
kh
1
to second hidden
neuron α
kh
2
and set a as the connection weight.
(iii) connect second hidden neuron α
kh
2
to output
neuron α
ko
and set a as the connection weight.
Step 4 (Connections and Weights). Let α
k
,
α
l
∈AR. For each attack relation (α
k
, α
l
)∈
attacks, do (i) ∼ (iii).
(i) connect input neuron α
ki
to first hidden neuron
α
lh
1
and set -b as the connection weight.
(ii) connect first hidden neuron α
kh
1
to second
hidden neuron α
lh
2
and set -b as the connection
weight.
(iii) connect second hidden neuron α
kh
2
to output
neuron α
lo
and set -1 as the connection weight.
Step 5 (Threshold). For each argument α
k
∈AR
(1≤k≤n), Set A (α
k
)·b as the threshold θ
α
k
of the
second hidden neuron α
kh
2
.
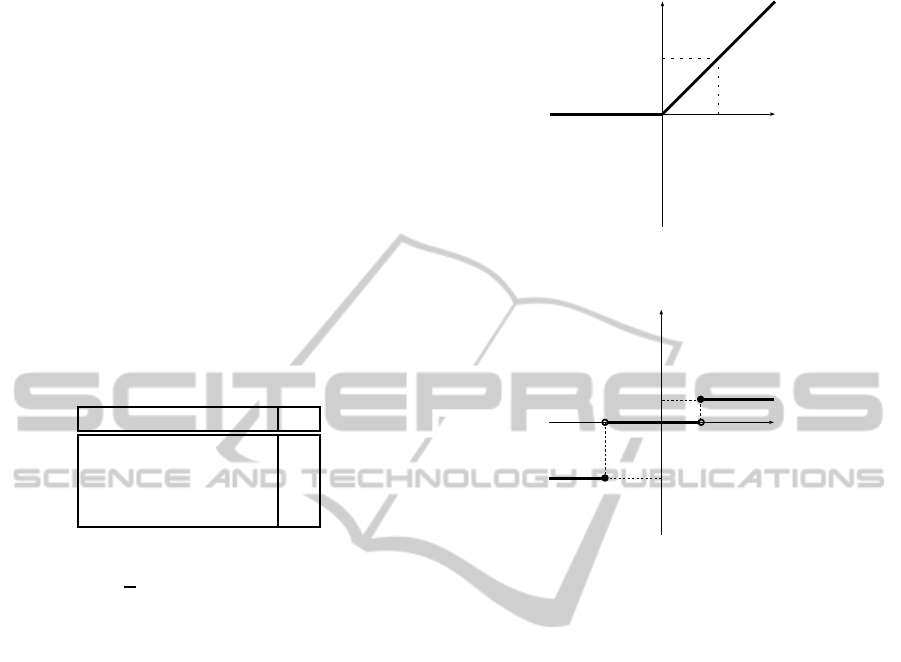
Step 6 (Activation Function of Input Neurons).
Set i(x) as the activation function of the input neu-
rons as follows (cf. Figure 3):
i(x) =
x (x ≥ 0)
0 (x < 0)
(1)
i(x)
x
1
0
1
Figure 3: Activation function i(x).
-b
-b
a
a
2
0
h(x)
x
Figure 4: Activation function h(x).
Step 7 (Activation Function of First Hidden Neu-
rons). Set h(x) as the activation function of the
first hidden neurons as follows (cf. Figure 4):
h(x) =
a (x ≥a
2
)
0 (−b < x < a
2
)
−b (x ≤ −b)
(2)
Step 8 (Activation Function of Second Hidden
Neurons). Set g(x) as the activation function of
the second hidden neurons as follows (cf. Figure
5):
g(x) =
a (x ≥ θ
α
k
)
0 (x < θ
α
k
)
(3)
Step 9 (Activation Function of Output Neurons).
Set f(x) as the activation function of the output
neurons as follows (cf. Figure 6):
f(x) =
a (x ≥a)
0 (−a < x < a)
−a (x ≤−a)
(4)
All A F can be translated to N by the translation al-
gorithm above. Then N must be a 4-layer neural net-
work. However, the number of neurons is not con-
stant. In detail, the number of neurons equals 4 times
the number of the arguments.
NCTA 2011 - International Conference on Neural Computation Theory and Applications
8
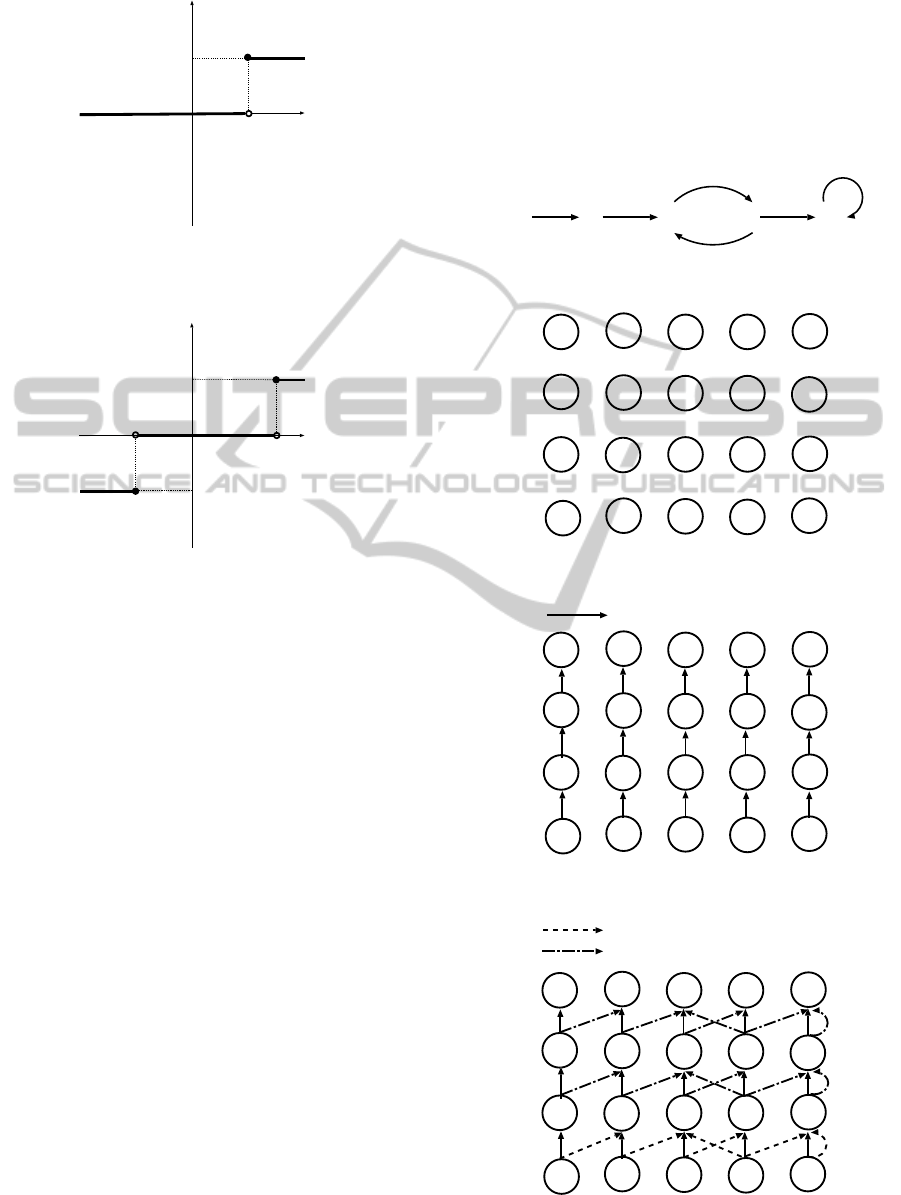
g(x)
x
0
a
θ
α
k
Figure 5: Activation function g(x).
f(x)
x
a
2
0
a
-a
-a
Figure 6: Activation function f(x).
The starting point of the idea of the architectute
for constructing the neural network comes from the
notion of defend. According to the definition 4, at
least two attack relations are required for it. Then we
can gain an attack relation between two neurons. Sim-
ilarly, we can gain two attack relations in the three
neurons. Threrefore 3-layer neural network can im-
plement the notion of defend. And the threshold of
the second hidden layer is specified by the number
of attack relations and defines the notion of de fend
and conflict − free. For this reason, 3-layer neu-
ral network from input layer to second hidden layer
can compute the admissible set, complete extension,
and grounded extension. However, for the purpose of
the computing the stable extension, we add the output
layer. Thus we construct the 4-layer neural network
in this idea. In addition all settings are required so
that the neural network computes argumentation se-
mantics. For this reason, the neural network includes
the characterictic function F(cf. Definition 5) and a
capability of checking conflict − free (cf. Definition
3).
And the argumentation semantics is computed via
checking an input vector converted from a set of argu-
ments (S∈AR) (cf.Definition12) and an output vector
which is finally output by N . The criteria for check-
ing the argument semantics is described in 3.3.
An example of the translation from A F to N is
seen in Example 4.
Example 4 (Translation from A F to N ). An ex-
ample of the translation from A F in Figure 2 to N
is as follow:
Step 1.
B DA C E
Step 2.
A
i
A
h
1
A
h
2
A
O
B
O
C
O
D
O
E
O
B
h
2
B
h
1
B
i
C
h
2
C
h
1
C
i
D
i
D
h
1
D
h
2
E
h
2
E
h
1
E
i
Step 3.
A
i
A
h
1
A
h
2
A
O
B
O
C
O
D
O
E
O
B
h
2
B
h
1
B
i
C
h
2
C
h
1
C
i
D
i
D
h
1
D
h
2
E
h
2
E
h
1
E
i
:weight is a
Step 4.
A
i
A
h
1
A
h
2
A
O
B
O
C
O
D
O
E
O
B
h
2
B
h
1
B
i
C
h
2
C
h
1
C
i
D
i
D
h
1
D
h
2
E
h
2
E
h
1
E
i
:weight is -b
:weight is -1
NEURAL NETWORKS COMPUTING THE DUNGEAN SEMANTICS OF ARGUMENTATION
9
Table 2: Threshold θ
α
k
Argument α
k
A (α
k
) Threshold θ
α
k
A 0 0
B 1 b
C 2 2b
D 1 b
E 2 2b
Step 5. Thresholds for each argument are shown in
Table 2.
Step 6 ∼ Step 9. Set the activation function to each
neuron.
3.2 Calculating Argumentation
Semantics by using N
In this subsection, we introduce notions and rules for
calculating the argumentation semantics by N .
Notation (Notation of Input-output Values of Neu-
rons). Let α
k
∈ AR. We represent the input values
of neurons as I
α
kX
and similarly the output as O
α
kX
(see Table 1 for X). The Figure 7 represents the input-
output values of neurons.
weight is a
weight is -b
weight is -1
I
α
ko
α
ko
O
α
ko
α
kh
2
I
α
kh
2
O
α
kh
2
α
kh
1
I
α
kh
1
O
α
kh
1
I
α
ki
α
ki
O
α
ki
...
...
...
...
...
...
Figure 7: Representation of the input-output values of neu-
rons
An input vector is given to N at first and used for
judging the argumentation semantics. The vector is
defined in the following Definition 12.
Definition 12 (First Input Vector I ). Let |AR| = n
and S ⊆ AR. A function I from a set of arguments to
input vector is defined as follws:
• I : 2
AR
→ {a, 0}
n
• I (S) = [I
α
1i
, I
α
2i
, ..., I
α
ni
], I
α
ki
=
a (α
k
∈S)
0 (α
k
6∈S)
Example 5 (First Input Vector). Let Figure 2 be an
argumentation framework and S={A,C, E} . The first
input vector I (S) = [a, 0, a, 0, a] by Definition 12.
Only when calculating the grounded extension, an
output vector is fed back as an input vector until N
gets to be a converging state (cf. Definition 14). The
following notions are necessary for the feedbacks.
Definition 13 (Time Round τ). In the computation
with a neural network N , the passage of time till the
output-vector is read off at the output-neurons since
the input-neurons are given an input-vector is called
time round, symbolically denoted τ. It has 0 as initial
value, and is incremented by 1 every time on input-
vector is recurrently given to N .
Definition 14 (Converging State of N ). If the
input-vector given to N is identical with the output-
vector read off at the same τ, the computation of N is
said to be in a converging state.
3.3 Argumentation Semantics in
N
The following definitions show how to interpret a re-
sult of computation of N and determine the argu-
mentation semantics of N . The argumentation se-
mantics in N can be defined only using the input-
output vectors except the grounded extension. Let
k be a natural number, | AR |= n, the first input
vector be [i
1
, i
2
, i
3
, ..., i
n
] and the output vector be
[o
1
, o
2
, o
3
, ..., o
n
].
Definition 15 (Admissible Set in N ). A set S⊆AR
is an admissible set in N iff ∀k(i
k
= a →o
k
= a).
Example 6. Let S = {D}. The input-output vector in
the translated N from Figure 2 (cf. Example 4) is the
following:
First Input Vector. [0, 0, 0, a, 0]
Output Vector. [a, 0, 0, a, 0]
According to Definition 15, {D} is an admissible set
in N .
Definition 16 (Complete Extension in N ). A set
S⊆AR is a complete extension in N iff ∀k(i
k
= a ↔
o
k
= a).
Example 7. Let S = {A, D}. The input-output vector
in the translated N from Figure 2 (cf. Example 4) is
the following:
NCTA 2011 - International Conference on Neural Computation Theory and Applications
10

First Input Vector. [a, 0, 0, a, 0]
Output Vector. [a, 0, 0, a, 0]
According to Definition 16, {A, D} is a complete ex-
tension in N .
Definition 17 (Stable Extension in N ). A
set S⊆AR is a stable extension in N iff
∀k(i
k
= a ↔o
k
= a) ∧ ∀l(i
l
= 0 →o
l
= −a).
Example 8. Let S = {A,C, E}. The input-output vec-
tor in the translated N from Figure 2 (cf. Example 4)
is the following:
First Input Vector. [a, 0, a, 0, a]
Output Vector. [a, −a, a, −a, a]
According to Definition 17, {A,C, E} is a stable ex-
tension in N .
Definition 18 (Grounded Extension in N ). Let S =
/
0. S
g
= {α
k
∈ AR | O
α
ko
=a in the converging state of
N } is the grounded extension.
Example 9. The input-output vector in the translated
N from Figure 2 (cf. Example 4) is the following:
When calculating the grounded extension, the first in-
put vector must be I (
/
0) = [0, 0, 0, 0, 0]. And the out-
put vector in the converging state of N is used for
checking the grounded extension.
First Input Vector. [0, 0, 0, 0, 0]
Output Vector. [a, −a, 0, 0, 0]
According to Definition 18, {A} is a grounded exten-
sion in N .
3.4 Soundness of Neural Network
Argumentation
The follwing theorem states that the computation of
the neural network provides a sound computation in
the sense that it yields the same extension as Dung’s
semantics.
Theorem 1. Let S ∈ AR. S is an extension of argu-
mentation semantics calculated in N iff S is an exten-
sion of the argumentation semantics in A F .
Due to the space limitation, we will not describe
the details of the proof (see Chapter 5 in (Gotou,
2010)). The idea of the proof is showing the sound-
ness of the definition of the threshold θ
α
k
. Be-
cause the threshold defines the notion of defend
and conflict − free and argumentation semantics are
mostly defined by them.
Figure 8: A program behavior from Step 1 to Step 4.
4 IMPLEMENTATION
In this section, we briefly describe an implementa-
tion of the neural network argumentation by using its
program results. When the program receives A F , it
outputs all extensions for each semantics(Admissible,
Complete, Stable, Grounded). The following is the
flow of the program.
Step 1. Input the number of arguments.
Step 2. Arguments named in alphabetical order are
generated.
Step 3. Input the name of an argument which is at-
tacked for each argument, otherwise type’0’.
Step 4. After inputting every counterargument,all at-
tack relations are output.
Step 5. Input-output values of neurons are output for
every calculation process.
Step 6. All extensions for each semantics are output.
Here, we will show an example of the
program behavior, assuming the pro-
gram receives A F =h{A, B,C, D, E},
{(A, B), (B,C), (C, D), (D,C), (D, E), (E, E)}i which
is given in Figure 2. An example of the program
behavior from Step 1 to Step 4 is given in Figure 8.
Now we calculate some semantics for A F . There
are 5 arguments and therefore we input 5 (Step 1).
Thereupon 5 arguments (named A, B, C, D, E) are
generated (Step 2). Then we input the name of an ar-
gument which is attacked. For the argument A in this
example, A attacks B and has no more arguments it at-
tacks. Accordingly, we input B at first and next, input
NEURAL NETWORKS COMPUTING THE DUNGEAN SEMANTICS OF ARGUMENTATION
11
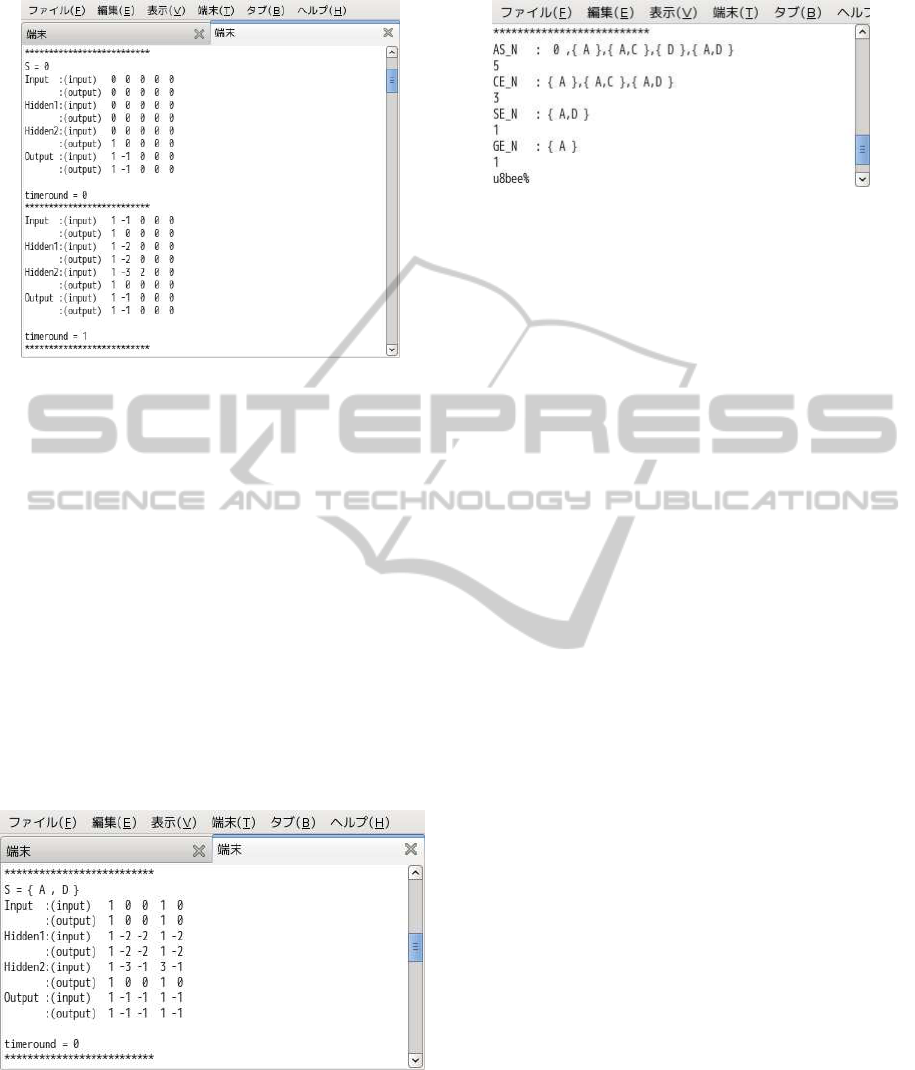
Figure 9: Computation process (1).
0 (Step 3). After inputting every counterargument, all
attack relations are outputted (Step 4).
We set 1 as a and 2 as b in the implementa-
tion. The following shows the computation process
for checking the grounded extension (input S=
/
0). See
Figure 9. The vectors in lines represent the input-
output values of each neuron and are listed in alpha-
betical order about arguments and the top is the input
and the bottom is the output. Calculating only the
grounded semantics, the output vector is fed back as
a new input vector. In the time round 1, the input vec-
tor equals to the output vector. We can regard it as
a converging state of N . Thus {A} is the grounded
extension in N by Definition 18.
The computation process for input S = {A, D} is
shown in Figure 10. According to Definition 15, 16
Figure 10: Computation process (2).
and 17, {A, D} are admissible, complete and stable.
The results of all extensions of the argumentation
semantics is shown as Figure 11. We need the power-
of-AR computations in N in order to get all exten-
sions of the argumentation semantics.
Figure 11: Results of argumentation semantics.
5 PREVIOUS WORK
Previously, Makiguchi and Sawamura proposed the
neural network that computes the Dungean argu-
mentation semantics (Makiguchi and Sawamura,
2007a)(Makiguchi and Sawamura, 2007b). How-
ever, it turned out that the neural network can-
not compute the Dungean argumentation semantics
in some abstract argumentation framework. For
example, let be h {A, B,C}, {(B, A), (C, B)} i an
argumentation framework shown in Figure 1 and
S = {A,C}. According to the study (Makiguchi
and Sawamura, 2007a)(Makiguchi and Sawamura,
2007b), first input vector =[1, 0, 1] and input vector
=[0, −1, 1].This means that {A,C} is not justified in
admissible set by the work (Makiguchi and Sawa-
mura, 2007a)(Makiguchi and Sawamura, 2007b).
However, according to the definition 6, {A,C} should
be justified in admissible set. Thus the neural network
cannot compute some extensions correctly. On the
other hand the neural network we proposed can com-
pute all extensions. In the same example, first input
vector =[a, 0, a] and input vector =[a, −a, a]. Accord-
ing to the definition 15, {A,C} is justified in admissi-
ble set as well as Dungean argumentation semantics.
For this reason, there are several differences between
our work and the work (Makiguchi and Sawamura,
2007a)(Makiguchi and Sawamura, 2007b). And the
main differences are shown as follws:
• The former architecture is 3-layer neural network
but the latter is 4-layer.
• The former neural network is completely defined
by invariable but the latter is mostly defined by
variable.
• The former neural network needs the definition of
types of attack relation but the latter doesn’t.
• The former is the recurrent neural network but the
latter is the feedforward neural network (except
the computation of the grounded extension).
• The former neural network cannot compute some
NCTA 2011 - International Conference on Neural Computation Theory and Applications
12

extensions but the latter can compute all exten-
sions.
The neural network we proposed is constructed so
that it can compute the Dungean argumentation se-
mantics correctly. And the Dungean argumentation
semantics is defined by the notions of defend and
conflict-free mainly. For this reason, all parameters
are set up so that the notions are implememted into
the neural network.
6 RELATED WORK
D’Avila Garcez et al. initiated a novel approach to
argumentation, called the neural network argumen-
tation (Garcez et al., 2005). However, the semantic
analysis for it is missing there. That is, it is not clear
what they calculate by their neural network argumen-
tation.
Besnard and Doutre proposed three symbolic ap-
proaches to checking the acceptability of a set of ar-
guments (Besnard and Doutre, 2004), in which not all
of the Dungean semantics can be dealt with. So it
may be fair to say that our approach with the neural
network is more powerful than Besnard et al.’s meth-
ods.
Vreeswijk and Prakken proposed a dialectical
proof theory for the preferred semantics (Vreeswijk
and Prakken, 2000). It is similar to that for the
grounded semantics (Prakken and Sartor, 1997), and
hence can be simulated in our neural network as well.
H¨olldobler and his colleagues gave a method to
encode a logic program to a 3-layer recurrent neu-
ral network and compute the least fixed point of
it (H¨olldobler and Kalinke, 1994) in the seman-
tics of logic programming. We, on the other hand,
constructed a 4-layer neural network, but our neu-
ral network computes not only the least fixed point
(grounded semantics) but also the fixed points (com-
plete extension) in the argumentation semantics.
7 CONCLUDING REMARKS
It is a long time since connectionism appeared as an
alternative movement in cognitive science or com-
puting science which hopes to explain human intel-
ligence or soft information processing. It has been a
matter of hot debate how and to what extent the con-
nectionism paradigm constitutes a challenge to classi-
cism or symbolic AI. On the other hand, much effort
has been devoted to a fusion or hybridization of neu-
ral net computation and symbolic one (Jagota et al.,
1999).
In this paper, we proposed a neural network which
computes all extensions of an argumentation seman-
tics exactly for every argumentation framework and
showed the soundness of neural network argumenta-
tion. The results yield a strong evidence to show that
such a symbolic cognitive phenomenon as human ar-
gumentation can be captured within an artificial neu-
ral network.
With the neural argumentation framework pre-
sented in the paper, we showed that symbolic dialec-
tical proof theories can be obtained from the neural
network computing various argumentation semantics,
which allow to extract or generate symbolic dialogues
from the neural network computation under various
argumentation semantics. The results illustrate that
there can exist an equal bidirectional relationship be-
tween the connectionism and symbolism in the area
of computational argumentation (Gotou et al., 2011).
The simplicity and efficiency of our neural net-
work may be favorable to our future plan such as
introducing learning mechanism into the neural net-
work argumentation, implementing the neural net-
work engine for argumentation, and so on. Specif-
ically, it might be possible to take into account the
so-called core method developed in (H¨olldobler and
Kalinke, 1994) and CLIP in (Garcez et al., 2009) al-
though our neural-symbolic system for argumentation
is much more complicated due to the complexitiesand
varieties of the argumentation semantics.
The neural argumentation framework allows to
build an Integrated Argumentation Environment
(IAE) based on the logic of multiple-valued argumen-
tation (Takahashi and Sawamura, 2004), powered by
the neural network. We are planning to incorporate
the neural argumentation framework to IAE.
REFERENCES
Besnard, P. and Doutre, S. (2004). Checking the accept-
ability of a set of arguments. In 10th International
Workshop on Non-Monotonic Reasoning (NMR 2004,
pages 59–64.
Caminada, M. (2006). Semi-stable semantics. In Dunne,
P. E. and Bench-Capon, T. J. M., editors, Computa-
tional models of argument: proceedings of COMMA
2006, volume 144 of Frontiers in Artificial Intelli-
gence and Applications, pages 121–130. IOS Press.
Caminada, M. (2008). A gentle intro-
duction to argumentation semantics.
http://icr.uni.lu/caminada/publications/Semantics Intr
oduction.pdf.
Ches˜nevar, C. I., Maguitman, G., and Loui, R. P. (2000).
Logical models of argument. ACM Computing Sur-
veys, 32:337–383.
NEURAL NETWORKS COMPUTING THE DUNGEAN SEMANTICS OF ARGUMENTATION
13

Dung, P. M. (1995). On the acceptability of arguments and
its fundamental role in nonmonotonic reasoning, log-
ics programming and n-person games. Artificial Intel-
ligence, 77:321–357.
Garcez, A. S. D., Gabbay, D. M., and Lamb, L. C.
(2005). Value-based argumentation frameworks as
neural-symbolic learning systems. Journal of Logic
and Computation, 15(6):1041–1058.
Garcez, A. S. D., Lamb, L. C., and Gabbay, D. M. (2009).
Neural-symbolic cognitive reasoning. Springer.
Gotou, Y. (2010). Neural networks calculating Dung’s
argumentation semantics. http://www.cs.ie.niigata-
u.ac.jp/Paper/Storage/graduation thesis gotou.pdf.
Gotou, Y., Hagiwara, T., and Sawamura, H. (2011). Ex-
tracting argumentative dialogues from the neural net-
work that computes the dungean argumentation se-
mantics. In 7th International Workshop on Neural-
Symbolic Learning and Reasoning (NeSy11). To be
presented at NeSy11.
H¨olldobler, S. and Kalinke, Y. (1994). Toward a new
massively parallel computational model for logic pro-
gramming. In Proc. of the Workshop on Combining
Symbolic and Connectionist Processing, ECAL 1994,
pages 68–77.
Jagota, A., Plate, T., Shastri, L., and Sun, R. (1999). Con-
nectionist symbol processing: Dead or alive? Neural
Computing Surveys, 2:1–40.
Levine, D. and Aparicio, M. (1994). Neural networks for
knowledge representation and inference. LEA.
Makiguchi, W. and Sawamura, H. (2007a). A hybrid argu-
mentation of symbolic and neural net argumentation
(part i). In Argumentation in Multi-Agent Systems,
4th International Workshop, ArgMAS 2007, Revised
Selected and Invited Papers, volume 4946 of Lecture
Notes in Computer Science, pages 197–215. Springer.
Makiguchi, W. and Sawamura, H. (2007b). A hybrid argu-
mentation of symbolic and neural net argumentation
(part ii). In Argumentation in Multi-Agent Systems,
4th International Workshop, ArgMAS 2007, Revised
Selected and Invited Papers, volume 4946 of Lecture
Notes in Computer Science, pages 216–233. Springer.
Prakken, H. and Sartor, G. (1997). Argument-based ex-
tended logic programming with defeasible priorities.
J. of Applied Non-Classical Logics, 7(1):25–75.
Prakken, H. and Vreeswijk, G. (2002). Logical systems
for defeasible argumentation. In In D. Gabbay and F.
Guenther, editors, Handbook of Philosophical Logic,
pages 219–318. Kluwer.
Rahwan, I. and Simari, G. R. E. (2009). Argumentation in
artificial intelligence. Springer.
Takahashi, T. and Sawamura, H. (2004). A logic of
multiple-valued argumentation. In Proceedings of the
third international joint conference on Autonomous
Agents and Multi Agent Systems (AAMAS’2004),
pages 800–807. ACM.
Vreeswijk, G. A. W. and Prakken, H. (2000). Credulous
and sceptical argument games for preferred semantics.
Lecture Notes in Computer Science, 1919:239–??
NCTA 2011 - International Conference on Neural Computation Theory and Applications
14
