
CHARACTERIZING RELATIONSHIPS THROUGH
CO-CLUSTERING
A Probabilistic Approach
Nicola Barbieri, Gianni Costa, Giuseppe Manco and Ettore Ritacco
High Performance Computing and Networking Institute of the Italian National Research Council
v. Pietro Bucci 41C, Arcavacata di Rende (CS), Italy
Keywords:
Collaborative filtering, Recommender systems, Block clustering, Co-clustering.
Abstract:
In this paper we propose a probabilistic co-clustering approach for pattern discovery in collaborative filtering
data. We extend the Block Mixture Model in order to learn about the structures and relationships within pref-
erence data. The resulting model can simultaneously cluster users into communities and items into categories.
Besides its predictive capabilities, the model enables the discovery of significant knowledge patterns, such as
the analysis of common trends and relationships between items and users within communities/categories. We
reformulate the mathematical model and implement a parameter estimation technique. Next, we show how
the model parameters enable pattern discovery tasks, namely: (i) to infer topics for each items category and
characteristic items for each user community; (ii) to model community interests and transitions among topics.
Experiments on MovieLens data provide evidence about the effectiveness of the proposed approach.
1 INTRODUCTION
Collaborative Filtering (CF) is recently becoming the
dominant approach in Recommender Systems (RS).
In literature, several CF recommendation techniques
have been proposed, mainly focusing on the predic-
tive skills of the system. Recent studies (McNee et al.,
2006; Cremonesi et al., 2010) have shown that the fo-
cus on prediction does not necessarily helps in devis-
ing good recommender systems. Under this perspec-
tive, CF models should be considered in a broader
sense, for their capability to understand deeper and
hidden relationships among users and products they
like. Examples in this respect are user communi-
ties, item categories preference patterns within such
groups. Besides their contribution to the minimiza-
tion of the prediction error, these relationships are im-
portant as they can provide a faithful yet compact de-
scription of the data which can be exploited for better
decision making.
In this paper we present a co-clustering approach
to preference prediction and rating discovery, based
on the Block Mixture Model (BMM) proposed in (Go-
vaert and Nadif, 2005). Unlike traditional CF ap-
proaches, which try to discover similarities between
users or items using clustering techniques or ma-
trix decomposition methods, the aim of the BMM
is to partition data into homogeneous block enforc-
ing a simultaneous clustering which consider both
the dimension of the preference data. This approach
highlights the mutual relationship between users and
items: similar users are detected by taking into ac-
count their ratings on similar items, which in turn are
identified considering the ratings assigned by similar
users. We extended the original BMM formulation
to model each preference observation as the output
of a gaussian mixture employing a maximum likeli-
hood (ML) approach to estimate the parameter of the
model. Unfortunately, the strict interdependency be-
tween user and item cluster makes difficult the appli-
cation of traditional optimization approaches like EM.
Thus, we perform approximated inference based on a
variational approach and a two-step application of the
EM algorithm which can be thought as a good com-
promise between the semantic of the original model
and the computational complexity of the learning al-
gorithm.
We reformulate standard pattern discovery tasks
by showing how a probabilistic block model automat-
ically allows to infer patterns and trends within each
block. We show experimentally that the proposed
model guarantees a competitive prediction accuracy
with regards to standard state-of-the art approaches,
and yet it allows to infer topics for each item cate-
64
Barbieri N., Costa G., Manco G. and Ritacco E..
CHARACTERIZING RELATIONSHIPS THROUGH CO-CLUSTERING - A Probabilistic Approach.
DOI: 10.5220/0003656800640073
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 64-73
ISBN: 978-989-8425-79-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

gory, as well as to learn characteristic items for each
user community, or to model community interests and
transitions among topics of interests. Experiments on
both the Netflix and Movielens data show the effec-
tiveness of the proposed model.
2 PRELIMINARIES AND
RELATED WORK
User’s preferences can be represented by using a
M × N rating matrix R, where M is the cardinality of
the user-set U = {u
1
,··· ,u
M
} and N is the cardinal-
ity of the item-set I = {i
1
,··· ,i
N
}. The rating value
associated to the pair hu,ii will be denoted as r
u
i
. Typi-
cally the number of users and items can be very large,
with M >> N, and preferences values fall within a
fixed integer range V = {1,··· ,V}, where 1 denote
the lower interest value. Users tend to express their
interest only on a restricted number of items; thus,
the rating matrix is characterized by an exceptional
sparseness factor (e.g more than 95%). Let δ(u,i) be
a rating-indicator function, which is equals to 1 if the
user u has rated/purchased the item i, zero otherwise.
Let I (u) denote the set of products rated by the user
u: I(u) = {i ∈ I : δ(u, i) = 1}; symmetrically, U(i)
denotes the set of users who have expressed their pref-
erence on the item i.
Latent Factor models are the most representative
and effective model-based approaches for CF. The un-
derlying assumption is that preference value associ-
ated to the pair hu,ii can be decomposed considering
a set of contributes which represent the interaction be-
tween the user and the target item on a set of features.
Assuming that there are a set of K features which de-
termine the user’s interest on an given item. The as-
sumption is that a rating is the result of the influence
of these feature to users and items: ˆr
u
i
=
∑
K
z=1
U
u,z
V
z,i
,
where U
u,z
is the response of the user u to the feature
z and V
z,i
is the response on the same feature of the
item i.
Several learning schema have been proposed to
overcome the sparsity of the original rating matrix
and to produce accurate models. The learning phase
may be implemented in a deterministic way, via gra-
dient descent (Funk, 2006) or, following a proba-
bilistic approach, maximizing the log-likelihood of
the model via the Expectation Maximization algo-
rithm. The latter leads to the definition of the As-
pect Model(Hofmann and Puzicha, 1999), known
also as pLSA. According to the user community vari-
ant, the rating value r is conditionally independent
of the user’s identity given her respective commu-
nity Z; thus, the probability of observing the rat-
ing value r for the pair hu,ii can be computed as
p(r|u, i) =
∑
K
z=1
p(r|i, z)p(z|u), where P(z|u) mea-
sures how much the preference values given by u fits
with the behavior of the community z and p(r|i,z) is
the probability that a user belonging to the community
z assigns a rating value r on i.
Only a few co-clustering approaches have been
proposed for CF data. An application of the weighted
Bregman coclustering (Scalable CC) to rating data is
discussed in (George and Merugu, 2005). The two-
sided clustering model for CF (Hofmann and Puzicha,
1999) is based on the strong assumption that each
person belongs to exactly one user-community and
each item belong to one groups of items, and fi-
nally the rating value is independent of the user and
item identities given their respective cluster member-
ships. Let C =
{
c
1
,··· ,c
k
}
be the user-clusters and
let c(u) : U → C be a function that maps each user to
the respective cluster. Similarly, let D =
{
d
1
,··· ,d
L
}
be a set of disjoint item-clusters, and d(i) : I → D
is the corresponding mapping function. According to
the two-sided clustering model, the probability of ob-
serving the preference value r conditioned to the pair
hu,ii is the following:
p(r|u, i, c(u) = c, d(i) = d) = p(r|c, d)
where p(r|c, d) are Bernoulli parameters and the clus-
ter membership are estimated by employing a varia-
tional inference approach.
The Flexible Mixture Model (FMM) (Jin et al.,
2006) extends the Aspect and the two sided model, by
allowing each user/item to belong to multiple clusters,
which are determined simultaneously, according to a
coclustering approach. Assuming the existence of K
user clusters indexed by c and L item clusters, indexed
by d, and let p(c
k
) be the probability of observing
the user-cluster k with p(u|c
k
) being the probability
of observing the user profile u given the cluster k and
using the same notations for the item-cluster, the joint
probability p(u,i,r) is defined as:
p(u,i,r) =
C
∑
c=1
D
∑
d=1
p(c)p(d)p(u|c)p(i|d)p(r|c,d)
The predicted rating associated to the pair hu,ii is then
computed as:
ˆr
u
i
=
V
∑
r=1
r
p(u,i,r)
∑
V
r
0
=1
p(u,i,r
0
)
The major drawback of the FMM relies on the com-
plexity of the training procedure, which is connected
with the computation of the probabilities p(c,d|u,i,r)
during the Expectation step.
A coclustering extension of the LDA(Blei et al., 2003)
CHARACTERIZING RELATIONSHIPS THROUGH CO-CLUSTERING - A Probabilistic Approach
65

model for rating data have been proposed in (Porte-
ous et al., 2008): the Bi-LDA employs two interacting
LDA models which enforce the simultaneous cluster-
ing of users and items in homogeneous groups.
Other co-clustering approaches have been pro-
posed in the current literature (see (Shan and Baner-
jee, 2008; Wang et al., 2009) ), however their exten-
sion to explicit preference data, which requires a dis-
tribution over rating values, has not been provided yet.
3 A BLOCK MIXTURE MODEL
FOR PREFERENCE DATA
In this section, we are interested in:devising how
the available data fits into ad-hoc communities and
groups, where groups can involve both users and
items. Fig. Fig. 1 shows a toy example of prefer-
ence data co-clustered into blocks. As we can see,
a coclustering induces a natural ordering among rows
and columns, and it defines blocks in the rating matrix
with similar ratings. The discovery of such a structure
is likely to induce information about the population,
as well as to improve the personalized recommenda-
tions.
Formally, a block mixture model (BMM) can be
defined by two partitions (z, w) which, in the case of
preference data and considering known their respec-
tive dimensions, have the following characterizations:
• z = z
1
,··· ,z
M
is a partition of the user set U into
K clusters and z
uk
= 1 if u belongs to the cluster
k, zero otherwise;
• w = w
1
,··· ,w
N
is a partition of the item set I into
L clusters and w
il
= 1 if the item i belongs to the
cluster l, zero otherwise.
Given a rating matrix R, the goal is to determine such
partitions and the respective partition functions which
specify, for all pairs hu, ii the probabilistic degrees of
membership wrt. to each user and item cluster, in
such a way to maximize the likelihood of the model
given the observed data. According to the approach
described (Govaert and Nadif, 2005; Gerard and Mo-
hamed, 2003), and assuming that the rating value r
observed for the pair hu,ii is independent from the
user and item identities, fixed z and w, the generative
model can be described as follows:
1. For each u generate z
u
∼ Discrete(π
1
;...;π
K
)
2. for each i generate w
i
∼ Discrete(ψ
1
;...;ψ
L
)
3. for each pair (u, i):
• detect k and l such that z
uk
= 1 and w
il
= 1
• generate r ∼ N(µ
l
k
;σ
l
k
)
There are two main differences with respect to the
FMM model introduced in the related work. First
of all, in our model all cluster membership are as-
sumed given a-priori, whereas FMM models each
pair separately. That is, we assume that the clus-
ter memberships z
u
and w
i
are sampled once and for
all, whereas in the FMM model they are sampled for
each given pair (u, i). Thus, in the FMM model, a
use u can be associated to different clusters in differ-
ent situations. Although more expressive, this model
is prone to overfitting and makes the learning pro-
cess extremely slow. The second difference is in the
way we model the rating probability p(r|z,w). FMM
adopts the multinomial model, whereas we choose to
adopt the gaussian. The latter better weights the dif-
ference between the expected and the observed value:
i.e. larger values for |ˆr
u
i
− r
u
i
| introduce a penalty fac-
tor.
The corresponding data likelihood in the Block
Mixture can be modeled as
p(R,z,w) =
∏
u∈U
p(z
u
)
∏
i∈I
p(w
i
)
∏
(u,i,r)∈R
p(r|z
u
,w
i
)
and consequently, the log-likelihood becomes:
L
c
(Θ;R,z,w) =
K
∑
k=1
∑
u∈U
z
uk
logπ
k
+
+
L
∑
l=1
∑
i∈I
w
il
logψ
l
+
+
∑
hu,i,ri∈R
∑
k
∑
l
h
z
uk
w
il
logϕ(r; µ
l
k
,σ
l
k
)
i
where Θ represents the whole set of parameters
π
1
,...,π
K
, ψ
1
,...,ψ
L
, µ
1
1
,...,µ
L
K
, σ
1
1
,...,σ
L
K
and
ϕ(r; µ, σ) is the gaussian density function on the rat-
ing value r with parameters µ and σ, i.e., ϕ(r; µ; σ) =
(2π)
−1/2
σ
−1
exp
−1
2σ
2
(r − µ)
2
.
In the following we show how the model can be
inferred and exploited both for prediction and for pat-
tern discovery.
3.1 Inference and Parameter
Estimation
Denoting p(z
uk
= 1|u, Θ
(t)
) = c
uk
, p(w
il
= 1|i, Θ
(t)
) =
d
il
and p(z
uk
w
il
= 1|u,i,Θ
(t)
) = e
ukil
, The conditional
expectation of the complete data log-likelihood be-
comes:
Q(Θ;Θ
(t)
) =
K
∑
k=1
∑
u
c
uk
logπ
k
+
L
∑
l=1
∑
i
d
il
logψ
l
+
∑
hu,i,ri∈R
∑
k
∑
l
h
e
ukil
logϕ(r; µ
l
k
,σ
l
k
)
i
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
66
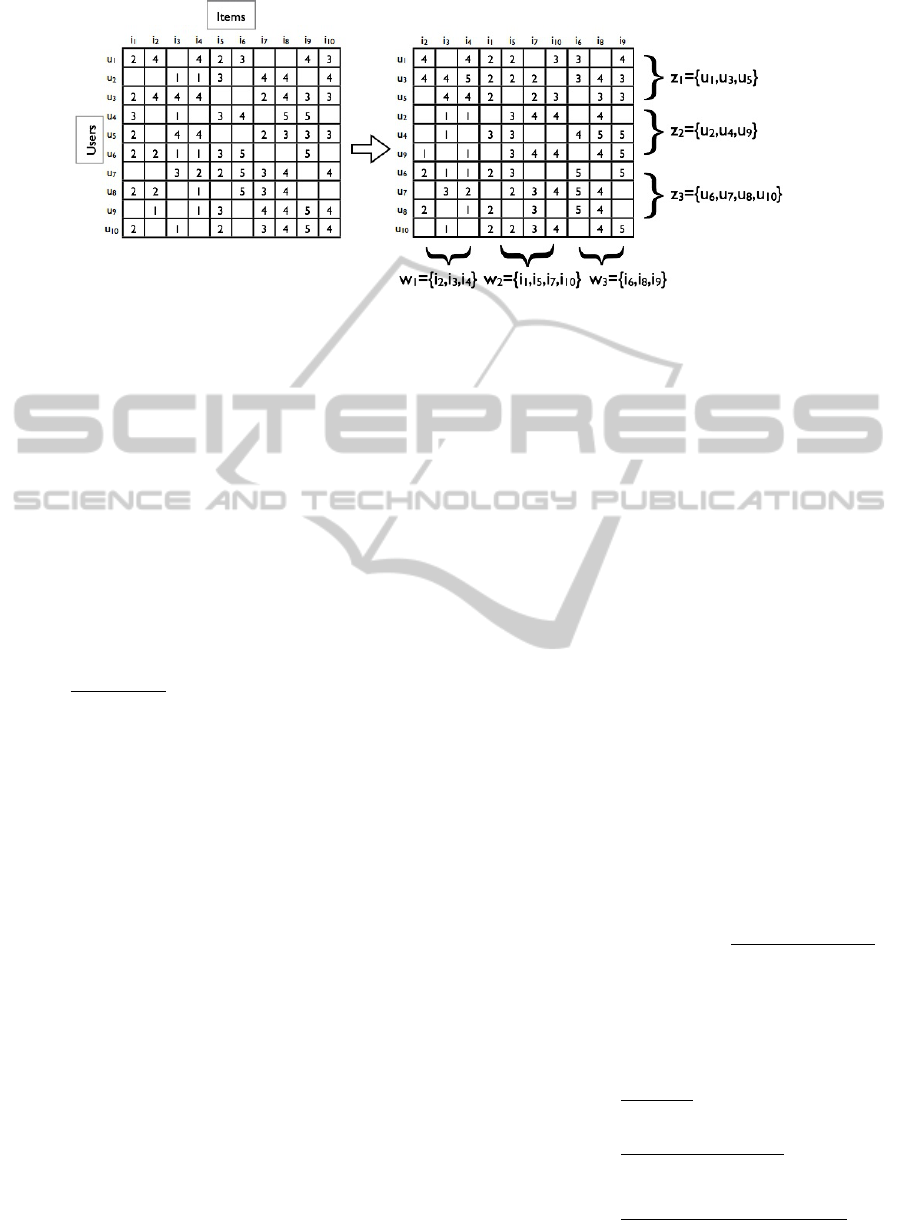
Figure 1: Example Co-Clustering for Preference Data.
As pointed out in (Gerard and Mohamed, 2003), the
above function is not tractable analytically, due to
the difficulties in determining e
ukil
; nor the adoption
of its variational approximation (e
ukil
= c
uk
· d
il
) al-
lows us to derive an Expectation-Maximization pro-
cedure for Q
0
(Θ,Θ
(t)
) where the M-step can be com-
puted in closed form. In (Gerard and Mohamed,
2003) the authors propose an optimization of the
complete-data log-likelihood based on the CEM al-
gorithm. We adapt the whole approach here. First
of all, we consider that the joint probability of a a
normal population x
i
with i = 1 to n can be factored
as:
∏
n
i=1
ϕ(x
i
;µ,σ) = h(x
1
,...,x
n
)∗ ϕ(u
0
,u
1
,u
2
;µ,σ),
where h(x
1
,...,x
n
) = (2π)
−n/2
, ϕ(u
0
,u
1
,u
2
;µ,σ) =
σ
−u
0
exp
2u
1
µ−u
2
−u
0
µ
2
2σ
2
and u
0
, u
1
and u
2
are the suf-
ficient statistics.
Based on the above observation, we can define a
two-way EM approximation based on the following
decompositions of Q
0
:
Q
0
(Θ,Θ
(t)
) = Q
0
(Θ,Θ
(t)
|d) +
∑
i∈I
L
∑
l=1
d
il
logψ
l
−
∑
u∈U
∑
i∈I (u)
d
il
/2log(2π)
where
Q
0
(Θ,Θ
(t)
|d) =
M
∑
u=1
K
∑
k=1
c
uk
(log(π
k
) + τ
uk
)
τ
uk
=
L
∑
l=1
log
ϕ(u
(u,l)
0
,u
(u,l)
1
,u
(u,l)
2
;µ
l
k
,σ
l
k
)
u
(u,l)
0
=
∑
i∈I (u)
d
il
; u
(u.l)
1
=
∑
i∈I (u)
d
il
r
u
i
u
(u,l)
2
=
∑
i∈I (u)
d
il
(r
u
i
)
2
Analogously,
Q
0
(Θ,Θ
(t)
) = Q
0
(Θ,Θ
(t)
|c) +
∑
u∈U
K
∑
k=1
c
uk
logπ
k
−
∑
i∈I
∑
u∈U(i)
c
uk
/2log(2π)
where
Q
0
(Θ,Θ
(t)
|c) =
N
∑
i=1
L
∑
l=1
d
il
(log(ψ
l
) + τ
il
)
τ
il
=
K
∑
k=1
log
ϕ(u
(i,k)
0
,u
(i.k)
1
,u
(i,k)
2
;µ
l
k
,σ
l
k
)
u
(i,k)
0
=
∑
u∈I (u)
c
uk
; u
(i,k)
1
=
∑
u∈I (u)
c
uk
r
u
i
u
(i,k)
2
=
∑
u∈I (u)
c
uk
(r
u
i
)
2
The advantage in the above formalization is that
we can approach the single components separately
and, moreover, for each component it is easier to esti-
mate the parameters. In particular, we can obtain the
following:
1. E-Step (User Clusters):
c
uk
= p(z
uk
= 1|u) =
p(u|z
k
) · π
k
∑
K
k
0
=1
p(u|z
k
0
) · π
k
0
p(u|z
k
) =
L
∏
l=1
ϕ(u
(u,l)
0
,u
(u.l)
1
,u
(u,l)
2
;µ
l
k
,σ
l
k
)
2. M-Step (User Clusters):
π
k
=
∑
u∈U
c
uk
M
µ
l
k
=
∑
M
u=1
∑
i∈I (u)
c
uk
d
il
r
u
i
∑
M
u=1
∑
i∈I (u)
c
uk
d
il
(σ
l
k
)
2
=
∑
M
u=1
∑
i∈I (u)
c
uk
d
il
(r
u
i
− µ
l
k
)
2
∑
M
u=1
∑
i∈I (u)
c
uk
d
il
CHARACTERIZING RELATIONSHIPS THROUGH CO-CLUSTERING - A Probabilistic Approach
67
3. E-Step (Item Clusters):
d
il
= p(w
il
= 1|i) =
p(i|w
l
) · ψ
l
∑
L
l
0
=1
p(i|w
l
0
) · ψ
l
0
p(i|w
l
) =
K
∏
k=1
ϕ(u
(i,k)
0
,u
(i,k)
1
,u
(i,k)
2
;µ
l
k
,σ
l
k
)
4. M-Step (Item Clusters):
ψ
l
=
∑
i∈I
d
il
N
µ
l
k
=
∑
N
i=1
∑
u∈U(i)
d
il
c
uk
r
u
i
∑
N
i=1
∑
u∈U(i)
d
il
c
uk
(σ
l
k
)
2
=
∑
N
i=1
∑
u∈U(i)
c
uk
d
il
(r
u
i
− µ
l
k
)
2
∑
N
i=1
∑
u∈U(i)
d
il
c
uk
3.2 Rating Prediction
The blocks resulting from a co-clustering can be di-
rectly used for prediction. Given a pair hu,ii, the
probability of observing a rating value r associated
to the pair hu, ii can be computed according to one of
the following schemes:
• Hard-Clustering Prediction:
p(r|i, u) = ϕ(r;µ
l
k
,σ
l
k
), where k =
argmax
j=1,··· ,K
c
u j
and l = argmax
h=1,···,L
d
ih
are the clusters that better represent the ob-
served ratings for the considered user and item
respectively.
• Soft-Clustering Prediction:
p(r|i, u) =
∑
K
k=1
∑
L
l=1
c
uk
d
il
ϕ(r; µ
l
k
,σ
l
k
), which
consists of a weighted mixture over user and item
clusters.
The final rating prediction can be computed by using
the expected value of p(r|u, i).
In order to test the predictive accuracy of the
BMM we performed a suite of tests on a sample of
Netflix data. The training set contains 5, 714, 427 rat-
ings, given by 435, 656 users on a set of 2, 961 items
(movies). Ratings on those items are within a range
1 to 5 (max preference value) and the sample is 99%
sparse. The test set contains 3, 773, 781 ratings given
by a subset of the users (389, 305) in the training set
over the same set of items. Over 60% of the users
have less than 10 ratings and the average number of
evaluations given by users is 13.
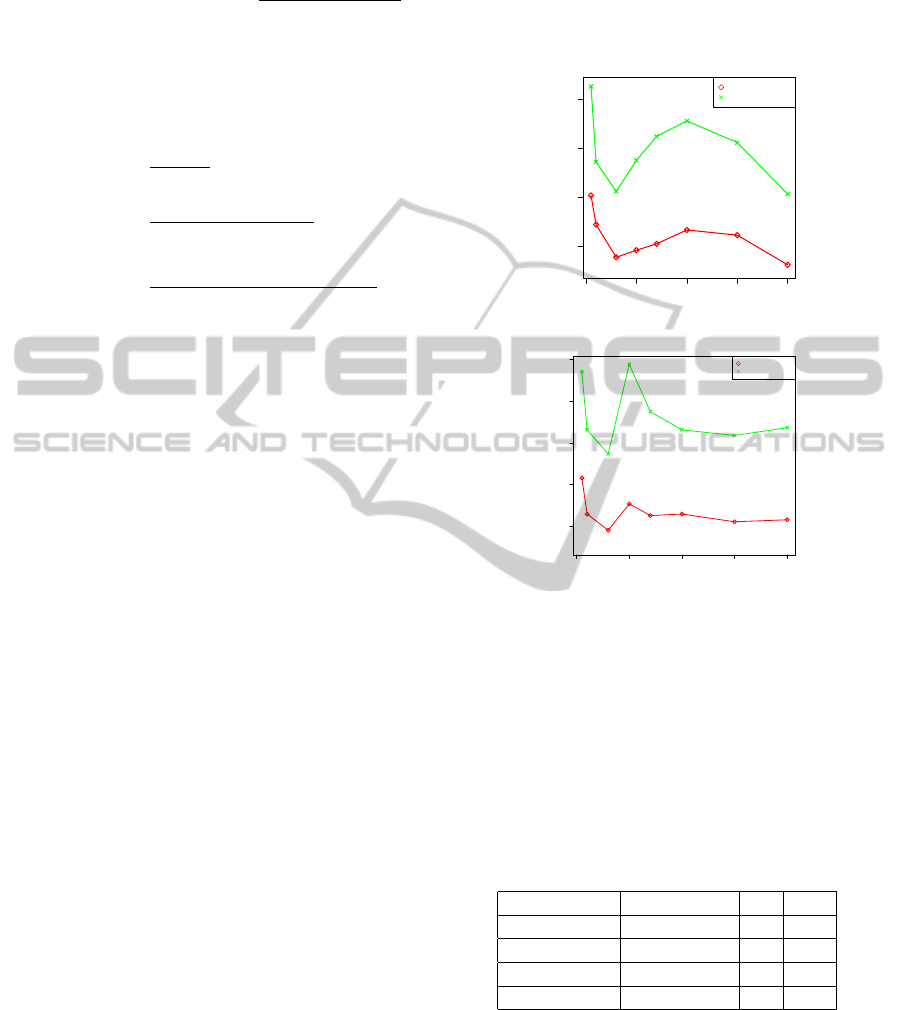
We evaluated the performance achieved by the
BMM considering both the Hard and the Soft predic-
tion rules and performed a suite of experiments vary-
ing the number of user and item clusters. Experiments
on the three models have been performed by retaining
the 10% of the training (user,item,rating) triplets as
held-out data and 10 attempts have been executed to
determine the best initial configurations. Performance
results measured using the RMSE for two BMM with
30 and 50 user clusters are showed in Fig. 2(a) and
Fig. 2(b), respectively. In both cases the soft cluster-
0 50 100 150 200
0.95 0.96 0.97 0.98
#Item Clusters
RMSE
Soft Clustering
Hard CLustering
(a) 30 user clusters
0 50 100 150 200
0.95 0.96 0.97 0.98 0.99
#Item Clusters
RMSE
Soft Clustering
Hard CLustering
(b) 50 userclusters
Figure 2: Predictive Accuracy of BMM.
ing prediction rule overcomes the hard one, and they
show almost the same trend. The best result (0.9462)
is achieved by employing 30 user clusters and 200
item clusters. We can notice from Tab. 1 that the re-
sults follow the same trend as other probabilistic mod-
els, like pLSA, which on the same portion of the data
achieves 0.9474 accuracy.
Table 1: RMSE of principal (co-)clustering approaches.
Method Best RMSE K H
BMM 0.946 30 200
PLSA 0.947 30 -
FMM 0.954 10 70
Scalable CC 1.008 10 10
4 PATTERN DISCOVERY USING
BMM
The probabilistic formulation of the BMM provides a
powerful framework for discovering hidden relation-
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
68
ships between users and items. As exposed above,
such relationships can have several uses in users seg-
mentation, product catalog analysis, etc. Several
works have focused on the application of clustering
techniques to discover patterns in data by analyzing
user communities or item categories. In (Jin et al.,
2004) authors showed how the pLSA model in its co-
occurrence version can be used to infer the underlying
task of a web browsing session and to discover rela-
tionships between users and web pages. Those ap-
proaches can be further refined by considering the co-
clustering structure proposed so far, which increases
the flexibility in modeling both user communities and
item categories patterns. Given two different user
clusters which group users who have showed a similar
preference behavior, the BMM allows the identifica-
tion of common rated items and categories for which
the preference values are different. For example, two
user community might agree on action movies while
completely disagree on one other. The identification
of the topics of interest and their sequential patterns
for each user community lead to an improvement of
the quality of the recommendation list and provide the
user with a more personalized view of the system. In
the following we will discuss examples of pattern dis-
covery and user/item profiling tasks.
The experiments in this section were performed
considering the 1M MovieLens dataset
1
, which con-
tains 1,000, 209 ratings given by 6, 040 users on ap-
proximately 3, 900 movies. Each user in this dataset
has at least 20 ratings and a list of genres is given for
each movie.The latter information will be used to val-
idate the the discovered block structure.
4.1 Co-clustering Analysis
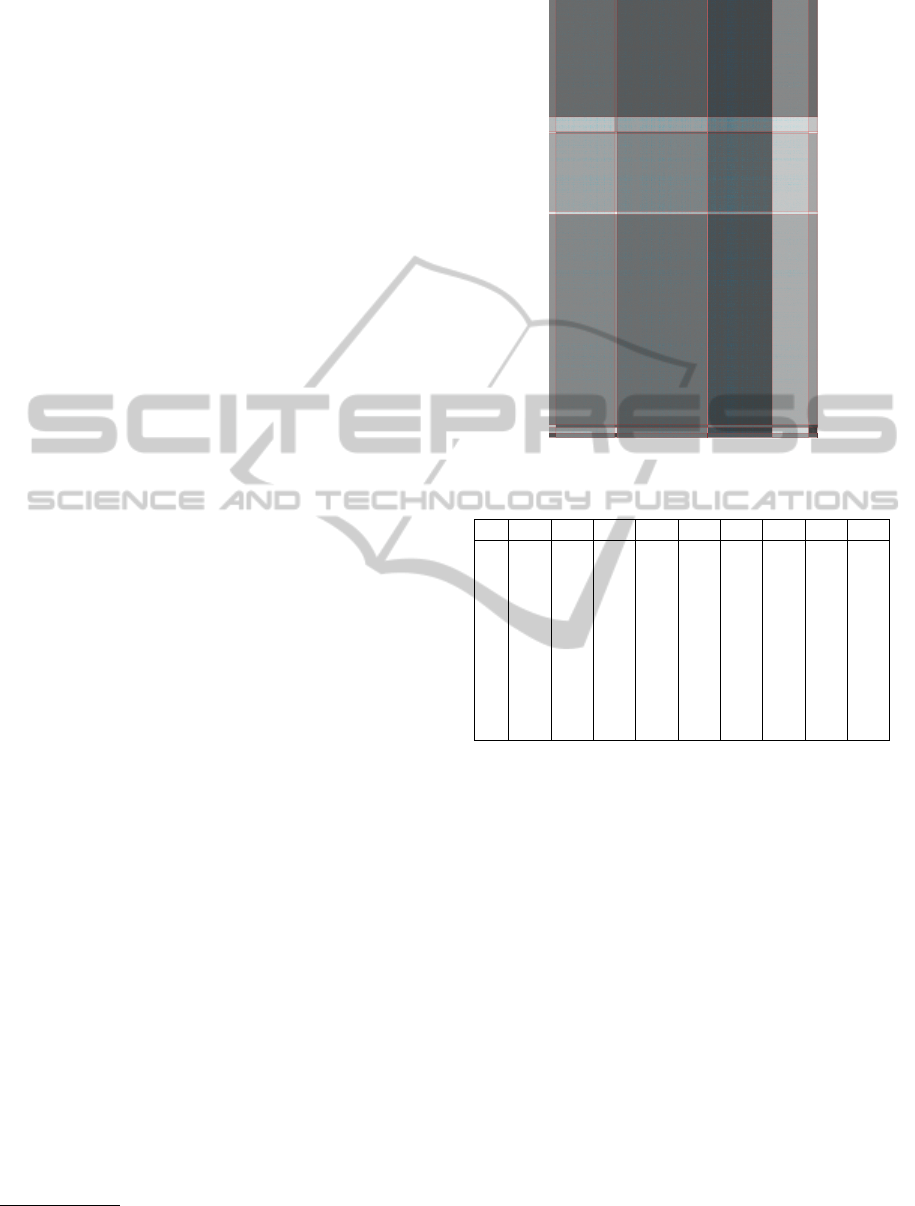
The relationships between groups of users and items
captured by the BMM can be easily recognized by
analyzing the distribution of the preference values
for each cocluster. Given a co-cluster hk,li, we can
analyze the corresponding distribution of rating val-
ues to infer the preference/interest of the users be-
longing to the community k on item of the category
l. Fig. 3 shows graphically a block mixture model
with 10 users clusters and 9 item clusters built on
the MovieLens dataset. A hard clustering assign-
ment has been performed both on users and clus-
ters: each user u has been assigned to the cluster
c such that c = argmax
k=1,···,K
c
uk
. Symmetrically,
each item i has been assigned to the cluster d such
that: d = argmax
l=1,···,L
d
il
. The background color
of each block hk,li describes both the density of rat-
1
http://www.grouplens.org/system/files/ml-data-
10M100K.tar.gz
Figure 3: Coclustering.
Table 2: Gaussian Means for each block.
d
1
d
2
d
3
d
4
d
5
d
6
d
7
d
8
d
9
c
1
3.4 3.59 3.59 4 2.91 4.43 3.59 2.93 3.65
c
2
2.23 2.2 2.92 2.79 2 3.45 2.07 1.80 2.51
c
3
2.11 3.24 3 3.66 2 4.17 1 1.03 5
c
4
2.45 2.69 2.54 3.2 2.43 3.74 2.51 2 2.56
c
5
1 1.79 1 2.32 1 2.98 1.66 1 1.75
c
6
2.93 3.07 3 3.57 2.20 4.09 2.9 2.3 3.16
c
7
1 3.56 3.9 3.7 3.64 3.39 4 3.49 2
c
8
2.25 2.26 1.62 3.27 1 4.17 4.54 1 2.45
c
9
4.08 3.24 4.40 3.54 5 4 3.71 4.5 5
c
10
1.91 2.82 1 2.7 4.3 2.2 1 4 2
ings and the average preference values given by the
users (rows) belonging to the k-th group on items
(columns) of the l-th category: the background inten-
sity increases with the average rating values of the co-
clusters, which are given in Tab. 2. Each point within
the coclusters represents a rating, and again an higher
rating value corresponds to a more intense color. The
analysis underlines interesting tendencies: for exam-
ple, users belonging to the user community c
1
tend
to assign higher rating values than the average, while
items belonging to item category d
6
are the most ap-
preciated. A zoom of portions of the block image is
given in Fig. 4(a) and in Fig. 4(b). Here, two blocks
are characterized by opposite preference behaviors:
the first block contains few (low) ratings, whereas the
second block exhibit a higher density of high value
ratings.
4.2 Item-topic Analysis
A structural property of interest is the item-topic de-
CHARACTERIZING RELATIONSHIPS THROUGH CO-CLUSTERING - A Probabilistic Approach
69

(a) Cocluster (c
5
,d
8
): Avg rating: 1
(b) Cocluster (d
1
,d
6
): Avg rating: 4.43
Figure 4: Cocluster Analysis.
pendency. Given a set of F topics G =
{
g
1
,···g
F
}
and assuming that each item is tagged with at least
one of those, we can estimate the relevance of each
topic within item clusters through a variant of the tf-
idf measure (Wu et al., 2008), namely topic frequency
- inverse category frequency (tf-icf ).
The topic frequency (similar to the term fre-
quency) of a topic g in a cluster d
l
can be defined as:
tf
g,d
l
=
∑
i∈d
l
δ(g∈Q
i
)
|Q
i
|
∑
u∈U
δ(u,i)
∑
F
g
0
=1
∑
i∈d
l
δ(g
0
∈Q
i
)
|Q
i
|
∑
u∈U
δ(u,i)
In a scenario, where items are associated with sev-
eral topics (genres), and where the number of topics
is much lower than size of the itemset, it is high likely
that all topics appear at least one in each item cate-
gory. According to this consideration, the standard
definition of idf would be useless for our purposes.
We, hence, provide an alternative formulation based
on entropy (Shannon, 1951), namely inverse category
frequency (icf ) for a topic g is:
ic f
g
= 1+ p(g) log
2
[p(g)]+[1− p(g)] log
2
[(1− p(g))]
Here, p(g) represent the prior probability of ob-
serving a item-genre and is computed as p(g) =
∑
L
l=1
p(g|d
l
) · p(d
l
), where p(g|d
l
) = t f
g,d
l
and
p(d
l
) = ψ
l
.
By combining the above definitions we can finally
obtain the tf-icf measure for a topic g in a category d
l
as:
tf-icf
g,d
l
= tf
g,d
l
× icf
g
We can also exploit the fact that BMM provides a soft
assignment to clusters, and provide an alternative ver-
sion of tf as:
tf
g,d
l
=
∑
i∈d
l
δ(g∈Q
i
)
|Q
i
)|
· d
il
∑
u∈U
δ(u,i)
∑
F
g
0
=1
∑
i∈d
l
δ(g
0
∈Q
i
)
|Q
i
)|
· d
il
∑
u∈U
δ(u,i)
The above considerations can be also applied to the
case of item frequency:
if
i,d
l
=
d
il
∑
u∈U
δ(u,i)
∑
i
0
∈d
l
d
i
0
l
∑
u∈U
δ(u,i
0
)
ic f
i
= 1 + p(i) log
2
[p(i)]
+[1 − p(i)]log
2
[(1 − p(i))]
where:
p(i) =
|U(i)|
|U|
The topic and item relevance described so far can
be directly employed to identify and measure the in-
terest of each user community into topics and items.
More specifically, we can measure the interest of a
user community c
k
for a topic g as:
CI
t
(c
k
,g) =
∑
L
l=1
µ
l
k
· tf-icf
g,d
l
∑
F
g
0
=1
∑
L
l=1
µ
l
k
· tf-icf
g
0
,d
l
The item-based counterpart follows straightfor-
wardly:
CI
i
(c
k
,j) =
∑
L
l=1
µ
l
k
· if-icf
j,d
l
∑
F
j
0
=1
∑
L
l=1
µ
l
k
· if-icf
j
0
,d
l
where j is the item target.
4.2.1 Evaluation
The MovieLens dataset provides for each movie a list
of genres. This information can be used to charac-
terize each item category, by exploiting the within-
cluster topic relevance discussed so far. The tf-icf
measure of observing each genre within each item
category is given in Tab. 3, where the dominant topic
is in bold.
The pie charts in Fig. 5(a), Fig. 5(b) and Fig. 5(c)
show the distribution on topics for different item clus-
ters. We can observe different patterns: d
2
is char-
acterized by a strong attitude for horror movies, an-
imation is the dominant topic in cluster 6, and d
8
is
summarized by the war genre. Finally, the cluster d
9
shows a predominance of drama movies. A summary
of the dominant genres in each item cluster, i.e., with
higher tf-icf, is given below:
Item Cluster Dominant Genre
d
1
Drama
d
2
Horror
d
3
Horror
d
4
Action
d
5
Drama
d
6
Animation
d
7
Comedy
d
8
War
d
9
Documentary
Fig. 6 shows the CI
t
(g,c
k
) values (in gray scale).
We can further analyze such values to infer the inter-
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
70

Table 3: tf-icf measures for each genre in each movie category
d
1
d
2
d
3
d
4
d
5
d
6
d
7
d
8
d
9
Action 0.03640 0 0.07375 0.06054 0.05152 0 0.05624 0.06966 0
Adventure 0.01981 0 0.04237 0.04339 0.03813 0 0.03828 0 0
Animation 0.01591 0 0.00660 0.00926 0.01801 0.24622 0.00999 0 0
Children’s 0.01581 0 0.03228 0.01643 0.02261 0 0.02855 0 0
Comedy 0.04137 0.03559 0.05403 0.05185 0.04730 0.06209 0.05685 0.10228 0
Crime 0.03319 0 0.01585 0.02217 0.01973 0 0.02515 0 0
Documentary 0.01423 0 0.00028 0.00053 0.00291 0 0.00341 0 0.94466
Drama 0.09777 0.00923 0.02308 0.05247 0.07720 0.04839 0.05099 0.06727 0
Fantasy 0.00553 0 0.01175 0.01579 0.01171 0 0.01559 0 0
Film-Noir 0.01485 0 0.00029 0.00123 0.00580 0 0.00113 0 0
Horror 0.01570 0.53057 0.08225 0.02691 0.01569 0 0.04014 0.03426 0
Musical 0.01739 0 0.00619 0.00914 0.02224 0 0.01088 0 0
Mystery 0.01697 0 0.00832 0.02757 0.00958 0 0.00952 0 0
Romance 0.03470 0 0.02395 0.05776 0.05092 0.09889 0.04625 0 0
Sci-Fi 0.02818 0 0.06247 0.04644 0.03843 0 0.04150 0 0
Thriller 0.04613 0 0.05851 0.05052 0.04771 0 0.05057 0 0
War 0.03902 0 0.01268 0.01041 0.01442 0.12291 0.00716 0.11860 0
Western 0.01653 0 0.00625 0.00704 0.00641 0 0.00875 0 0
(a) Item cluster 2 (b) Item cluster 6 (c) Item cluster 8
Figure 5: Topic Analysis on Item Clusters.
est of a user community for a given topic. In particu-
lar, a community exhibits a high interest for a topic if
the corresponding CI
t
value is sufficiently higher than
the average CI
t
value of all the other topics. Table
4 summarizes the associations among user communi-
ties and item topics. For example, users in c
8
exhibit
preferences for the Action and War genres.
4.3 User Profile Segmentation
The topics of interest of a user may change within
time and consecutive choices can influence each
other. We can analyze such temporal dependencies by
mapping each user’s choice into their respective item
cluster. Assume that movieLens data can be arranged
as a set { ¯u
1
,..., ¯u
M
}, where ¯u =
{
hr
u
i
,i,t
u
i
i∀i ∈ I (u)
}
and t
u
i
is the timestamp corresponding to the rating
given by the user u on the item i. By chronologically
sorting ¯u and segmenting it according to item clus-
ter membership, we can obtain a view of how user’s
Figure 6: Topic-Interests for User Communities.
tastes change over time. Three example of user pro-
file segmentation are given in the figures below (the
mapping between item categories and colors is given
CHARACTERIZING RELATIONSHIPS THROUGH CO-CLUSTERING - A Probabilistic Approach
71
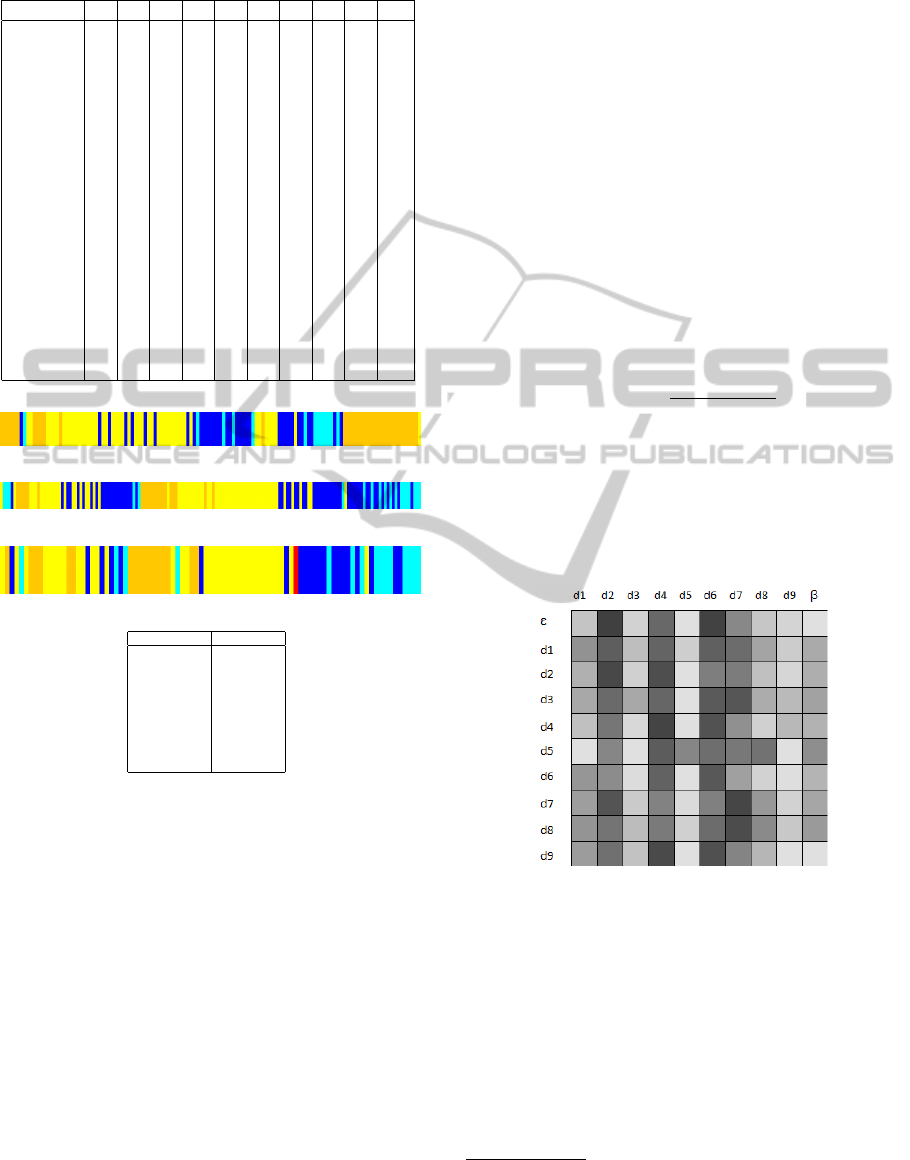
Table 4: Summary of Interests in Topics For User Commu-
nities.
c
1
c
2
c
3
c
4
c
5
c
6
c
7
c
8
c
9
c
10
Action y y y y y
Advent.
Animat. y y
Children’s
Comedy y y y y y y y y y y
Crime
Documen. y y y y y y y y y y
Drama y y y y y y y y y y
Fantasy
Noir
Horror y y y y y y y y y y
Musical
Mystery
Romance y y y
Sci-Fi
Thriller
War y y y
Western
(a)
(b)
(c)
Item Cluster Color
d
1
Red
d
2
Blue
d
3
Green
d
4
Yellow
d
5
Magenta
d
6
Orange
d
7
Cyan
d
8
Pink
d
9
Dark Grey
Figure 7: User Profile Segmentation.
by the included table).
In practice, we can assume that the three users
show a common attitude towards comedy and drama,
which are the dominant topics corresponding to the
colors yellow and orange. Notice, however, that users
(b) and (c) are prone to change their interest towards
comedy, as clearly shown by the change in color.
4.4 Modeling Topic Transitions
Based on the above observations, we aim at esti-
mating the sequential connections among topics: In
practice, we would like to analyze which item cate-
gories are likely to next capture the interests of a user.
Those sequential patterns can be modeled by exploit-
ing Markov Models. The latter are probabilistic mod-
els for discrete processes characterized by the Markov
properties. We adopt a Markov Chain property here,
i.e., a basic assumption which states that any future
state only depends from the present state. This prop-
erty limits the ‘memory’ of the chain which can be
represented as a digraph where nodes represent the
actual states and edges represent the possible transi-
tions among them.
Assuming that the last observed item category for
the considered user is d
i
, the user could pick an item
belonging to the another topic d
j
with probability
p(d
j
|d
i
). Thus, we need to estimate all the transition
probabilities, starting from a |L + 1| x |L + 1| transi-
tion count matrix T
c
, where T
c
(i, j) stores the number
of times that category j follows i in the rating profile
of the users.
2
The estimation we provide is rather simple, corre-
sponding to a simple frequency count:
p(d
j
|d
i
) =
T
c
(i, j)
∑
L+1
j=1
T
c
(i, j
0
)
Fig. 8 represents the overall transition probabil-
ity matrix, which highlights some strong connection
among given categories. As instance, the item cate-
gories having drama as dominant genre, d
4
, d
6
and d
9
are highly correlated as well as d
2
, d
7
and d
8
which
correspond to comedy movies.
Figure 8: Transition Probabilities Matrix.
It is interesting to compare how the transition
probabilities change within different user communi-
ties. Fig. 9 shows the transitions for three different
communities. Notice that, besides common transition
patterns, each community has some distinctive tran-
sitions that characterize their population. For all the
considered user communities, the most likely initial
item category is d
6
; while the first and the last com-
munity reproduced in the example show a strong at-
titude corresponding to the transition d
8
→ d
2
, this is
2
We assume two further states ε, representing the initial
choice, and β, representing the last choice.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
72

instead a weak pattern within c
7
. The same consider-
ation can be done for the transition d
9
→ d
7
, which is
strong for c
7
and c
10
, while users belonging to c
3
are
more prone to the transition towards d
6
.
(a) User community c
3
(b) User community c
7
(c) User community c
10
Figure 9: Transition Probabilities Matrix.
The analysis of the transition probabilities can be
hence exploited for generating new recommendations
enforcing topic diversity (Ziegler et al., 2005) in the
top-K lists of items by taking into account not exclu-
sively the current topic of interest but the ones that
more likely could be connected to it.
5 CONCLUSIONS AND FUTURE
WORKS
In this work we focused on the application of the
Block Mixture Model to Collaborative Filtering data.
This approach allows the simultaneous clustering of
users and items and could be used to identify and mea-
sure hidden relationships among them. The proposed
model provides a flexible and powerful framework to
analyze the users’ behavior. This information can be
used to improve the quality of a recommendation sys-
tem, as mentioned throughout the presentation. Fu-
ture works will focus on embedding baseline com-
ponents and normalization approaches that might be
employed to improve the quality of the clustering and
the prediction accuracy.
REFERENCES
Blei, D. M., Ng, A. Y., and Jordan, M. I. (2003). Latent
dirichlet allocation. The Journal of Machine Learning
Research, 3:993–1022.
Cremonesi, P., Koren, Y., and Turrin, R. (2010). Perfor-
mance of recommender algorithms on top-n recom-
mendation tasks. In RecSys, pages 39–46.
Funk, S. (2006). Netflix update: Try this at home.
George, T. and Merugu, S. (2005). A scalable collaborative
filtering framework based on co-clustering. In ICDM,
pages 625–628.
Gerard, G. and Mohamed, N. (2003). Clustering with block
mixture models. Pattern Recognition, 36(2):463–473.
Govaert, G. and Nadif, M. (2005). An em algorithm for
the block mixture model. IEEE Trans. Pattern Anal.
Mach. Intell., 27(4):643–647.
Hofmann, T. and Puzicha, J. (1999). Latent class models
for collaborative filtering. In IJCAI, pages 688–693.
Jin, R., Si, L., and Zhai, C. (2006). A study of mixture
models for collaborative filtering. Inf. Retr., 9(3):357–
382.
Jin, X., Zhou, Y., and Mobasher, B. (2004). Web usage min-
ing based on probabilistic latent semantic analysis. In
KDD, pages 197–205.
McNee, S., Riedl, J., and Konstan, J. A. (2006). Being
accurate is not enough: How accuracy metrics have
hurt recommender systems. In ACM SIGCHI Confer-
ence on Human Factors in Computing Systems, pages
1097–1101.
Porteous, I., Bart, E., and Welling, M. (2008). Multi-hdp:
a non parametric bayesian model for tensor factoriza-
tion. In AAAI, pages 1487–1490.
Shan, H. and Banerjee, A. (2008). Bayesian co-clustering.
In ICML.
Shannon, C. E. (1951). Prediction and entropy of printed
english. Bell Systems Technical Journal, 30:50–64.
Wang, P., Domeniconi, C., and Laskey, K. B. (2009). La-
tent dirichlet bayesian co-clustering. In ECML PKDD,
pages 522–537.
Wu, H. C., Luk, R. W. P., Wong, K. F., and Kwok, K. L.
(2008). Interpreting tf-idf term weights as making
relevance decisions. ACM Trans. Inf. Syst., 26:13:1–
13:37.
Ziegler, C.-N., McNee, S. M., Konstan, J. A., and Lausen,
G. (2005). Improving recommendation lists through
topic diversification. In WWW, pages 22–32.
CHARACTERIZING RELATIONSHIPS THROUGH CO-CLUSTERING - A Probabilistic Approach
73
