EEG NOISE CANCELLATION BASED ON NEURAL NETWORK

J. Mateo

, A. Torres

C. Soria

, Mª. García

and C. Sánchez

Innovation in Bioengineering Research Group, University of Castilla-La Mancha, Cuenca, Spain

Clinical Neurophysiology Service, Virgen de la Luz Hospital (SESCAM), Cuenca, Spain

Keywords: Biomedical signals, Muscle noise, Electrocardiogram, Neural network.

Abstract: Electroencephalogram (EEG) recordings often experience interference by different kinds of noise, including

white and muscle, severely limiting its utility. Artificial neural networks (ANNs) are effective and powerful

tools for removing interference from EEGs, but the quality of the separation is highly dependent on the type

and degree of contamination. Several methods have been developed, but ANNs appear to be the most

effective for reducing muscle contamination, especially when the contamination is greater in amplitude than

the brain signal. We propose an ANN as a filter for EEG recordings, developing a novel framework for

investigating and comparing the relative performance of an ANN incorporating real EEG recordings from

the Clinical Neurophysiology Service at the Virgen de la Luz Hospital in Cuenca (Spain). This method was

based on a growing ANN that optimised the number of nodes in the hidden layer and the coefficient

matrices, which were optimised by the simultaneous perturbation method. The ANN improved the results

obtained with the conventional EEG filtering techniques: wavelet, singular value decomposition, principal

component analysis, adaptive filtering and independent components analysis. The system was evaluated

within a wide range of EEG signals in which noise was added. The present study introduces a method of

reducing all EEG interference signals with low EEG distortion and high noise reduction.

1 INTRODUCTION

Noise reduction is a matter of considerable

importance in biomedical signal processing

applications, especially electroencephalogram

(EEG) analysis (Sörnmo, 2005); (Bronzino, 2000);

(Rangayyan, 2002).

Noncortical biological artifacts are the principal

source of contamination in EEG recordings and are

generated primarily by movements, cardiac pulse,

and muscle activity, particularly that of the face

(especially the jaw) and neck. EEG experimental

design is generally constrained by the desire to

minimise the effect of these artifacts.

Several methods have been suggested for muscle

noise reduction. Signal processing techniques used

for noise elimination include bandpass filtering, fast

Fourier transform, autocorrelation, autoregressive

modelling, adaptive filtering, Kalman filtering,

Bayesian filtering, singular value decomposition

(SVD) (Paul 2000); (Shao, 2009); (Zhang, 2006);

(Sameni, 2008) one of the common approaches is

the adaptive filtering (AF) architecture which has

been used for the noise cancellation of ECG (Olmos,

2002) and wavelet (Castellanos, 2006). Recently,

principal component analysis (PCA) (Lagerlund,

2004) and independent component analysis (ICA)

(Crespo-Garcia, 2008) have become popular for

analysing biomedical data. One of the main

advantages of these approaches relates to their

applicability to multisensory observations of mixed

signals. However, PCA is unable to separate some

artifact signals from brain signals when they have

similar amplitudes. In addition, both PCA and SVD

perform well only if the noise level is low enough

and a signal subspace and noise subspace are

orthogonal to each other. For practical applications,

the orthogonality requirement is usually not valid.

On the other hand, ICA cannot guarantee that some

individual independent components (ICs) contain

only noise and not information about useful sources,

especially in biomedical applications. Thus, the

problem of detection and filtering the "useful" part

of each IC is still open, and additional tools are

needed to solve it.

In the present study, we created an artificial

neural network (ANN) that can act as a filter for

EEG recordings. The network was trained using the

330

Mateo J., Torres A., Soria C., García M. and Sánchez C..

EEG NOISE CANCELLATION BASED ON NEURAL NETWORK.

DOI: 10.5220/0003657103300333

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 330-333

ISBN: 978-989-8425-84-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

simultaneous perturbation (SP) method. The ANN

was chosen mainly because of its adaptability to the

nonlinear and time-varying features of the noise.

This system was evaluated within a wide range of

EEG signals in which white noise and muscle noise

were added from the Clinical Neurophysiology

Service at Virgen de la Luz Hospital. Thus, this

algorithm could serve as an effective framework for

filtering noise in EEG recordings. We expect that the

distortion of this signal will be reduced compared to

conventional methodologies. The results

demonstrate that this method can maintain the

original shape of the EEG signal in very low SNR

conditions in which the brain signal is mixed with

the noise.

2 MATERIALS

The signals considered in the present study

originated from patients at the referred hospital. All

signals were recorded using Viasys Healthcare –

NicoletOne equipment, which had been

implemented within a concrete period of time. Sleep

studies were also included.

All signals obtained from the hospital were

randomly classified into three groups, and each of

them used a different phase in the filtering process

with ANN. Forty signals were chosen to integrate

the first group, which was used for network training.

The second group was used to validate and compare

proper ANN function, and the third group was used

to compare ANN with the other systems.

The first and second groups were comprised of

80 signals that lasted 25-50 minutes. Also, 10 sleep

testing of approximately eight hours, have been

included in these groups. These signals were filtered

through ICA (Crespo-Garcia, 2008) to remove any

current noise.

Once this process was completed, white and

muscle noise were sequentially added to the EEG

signal as defined by equation. 1, where d(k) is the

EEG signal after ICA filtering, A is the amplitude of

the added noise, and n(k) is the noise signal.

Amplitude A was modified in order to obtain an

SNR margin between -10dB and 30dB. The main

aim was to estimate the clean signal d(k) from the

noisy signal p(k). These recordings are synthetic

signals (EEG records to which different noises were

added).

p(k) = d(k) +An (k) (1)

The third group of signals was made up of 50

signals; 40 signals that lasted 30-60 minutes and 10

sleep testing of 8 hours, and neither noise nor

variation was added or modified in them (real

signals). These signals were also used to compare

the above mentioned methods to ANN.

3 METHOD

The Adaline network uses supervised learning and

involves a sum of products using the input and

weight vectors. An adaptive operation means that

there is a mechanism by which w

, v

can be adjusted,

usually iteratively, to achieve correct values.

Regarding Adaline, the properties of the perturbation

vectors are assumed to be as described by Maeda

and De Figueiredo (Maeda, 1997).

Figure 1: Proposed Neuronal Network with one neuron in

the hidden layer. The black coefficients are constants.

For every input, the network output differs from

the expected target value d

by (d

– p

), where p

the current output and n is the number of signals.

This network structure was initially made up of

three layers: an input layer, one hidden layer made

up of 40 neurons, and an output layer. Once this

network was trained, its work was re-evaluated and,

if necessary, more neurons added to the hidden layer

(Figure 1). This procedure was repeated until

expected results are obtained. At all these stages, the

ANN was adapted using the SP method in order to

obtain the best results. The process of training and

initialization was modified and implemented as

described by Maeda (Maeda, 1995, 1997). The

detailed strict convergence conditions of SP were

described by Spall (Spall ,1992).

3.1 Learning Algorithm using

Simultaneous Perturbation

Simultaneous perturbation technique for training

neural networks has been introduced by Spall (Spall,

1992). Other authors (Maeda, 1995) have also

reported results of similar methods. To adapt the

Input

Output

Hidden layer

EEG NOISE CANCELLATION BASED ON NEURAL NETWORK

331

weights of the system is necessary to consider the

gradient of the error function, this is:

∂

≅∇

)(

(2)

Defining the error function like:

()

)( dywJ −=

(3)

where;

()

dy −=

(4)

Using the equation (4) it is possible to measure the

error between the present exit and the wished exit.

On the other hand, the approach of differences is a

procedure known to obtain the derived from a

function, so this approach to reduce the complexity

can be used (Haykin, 1994). c is a perturbation

added to the i component (Maeda, 1997).

The neural network exit, Y, is a function of the

vector of weights:

wYfwYf

))(())(()( −

≈

∂

(5)

Nevertheless the above idea which is very simple,

needs more operations. It is due to evaluate

()

for

all the network weights to obtain the amount

modified for all the weights.

tttttt

VWYDVCWY

),(),( −++

=Δ

(6)

The weights of the neural network are adapted using

the following rule:





=



−∆



The best results have been obtained when 15

neurons were added to the hidden layer. When more

than 15 neurons are added, there is no improvement

of both the computational load and the noise

reduction.

4 RESULTS

Noise reduction is important for obtaining a clear

and useful signal. Some signals, such as EEG, are

non-stationary, and the noise statistical property is

complicated because of the complexity of the signal.

Different techniques have been proposed to reject

muscle noise in EEG signals; these conventional

filtering techniques can contain ripples that do not

correspond to the original EEG. ANN improves all

results obtained by wavelet, SVD, PCA, AF and

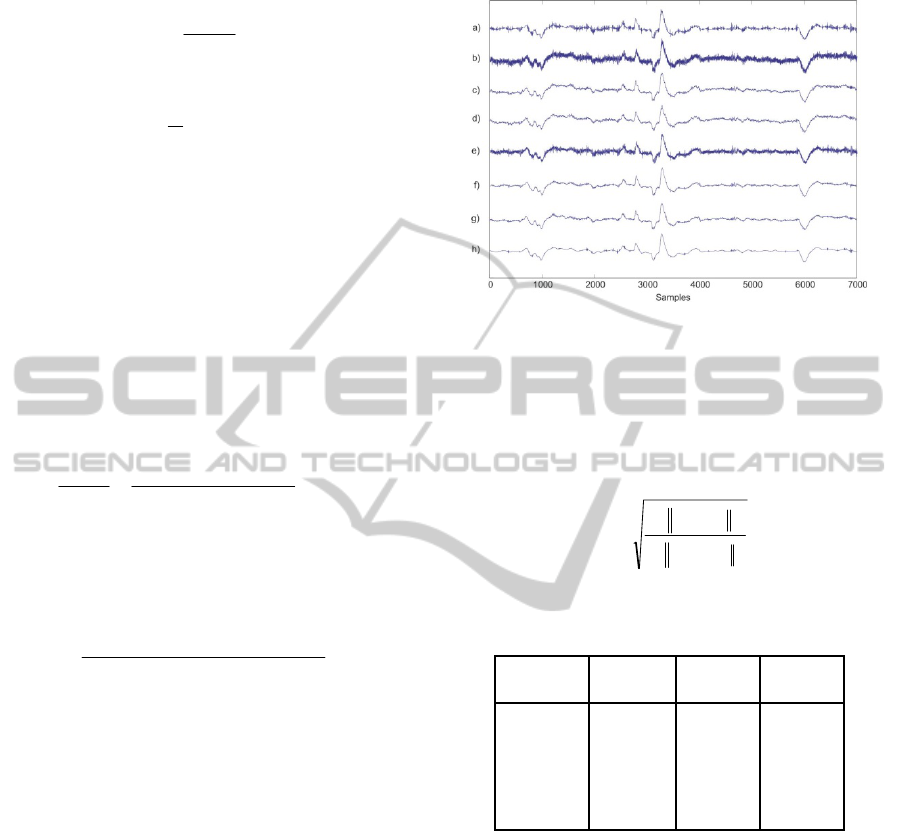
ICA, significantly reducing the interference, Figure

2. The methods are referred in introduction section.

Figure 2: Comparison of the muscle noise removal by

ANN and traditional techniques for F7-T3 derivation.

a) Original recording without processing. b) Input signal

of 8 dB muscle noise used to compare the different

methods. c) Filtering results for muscle noise with the

wavelet method. d) SVD method. e) PCA method. f) AF

method. g) ICA method and h) ANN

⎟

⎠

⎞

⎜

⎝

⎛

−

{

log20

xxE

SIR

out

(7)

Table 1: Obtained results of the cross correlation and SIR

for muscle noise, average values.

Methods

Synthetic

(CC)

Real(CC) SIR

Wavelet

SVD

PCA

ICA

ANN

03.085.0 ±

02.088.0 ±

04.082.0 ±

03.089.0 ±

02.091.0 ±

02.096.0 ±

03.082.0 ±

03.086.0 ±

03.080.0 ±

04.086.0 ±

03.088.0 ±

02.095.0 ±

2.19.12 ±

13.25.13 ±

3.15.12 ±

27.20.14 ±

5.12.15 ±

1.11.19 ±

Table 1 shows the cross-correlation average

values and standard deviation in synthetic signals

and real signals. Nevertheless table 1 shows the SIR

average values calculated for synthetic recordings.

Equation 7, shows SIR expression where x

shows

the input to the system, x

out

the exit and x the

original registry without noise. As can be seen from

table 1, with ANN the values are higher than the

values obtained with the other systems, both

synthetic signals and real signals.

Figure 3 shows the time-frequency analysis of

EEG signal with muscle noise. As can be seen the

ANN system reduces fluctuations due to muscle

noise and gets a more uniform signal.

NCTA 2011 - International Conference on Neural Computation Theory and Applications

332

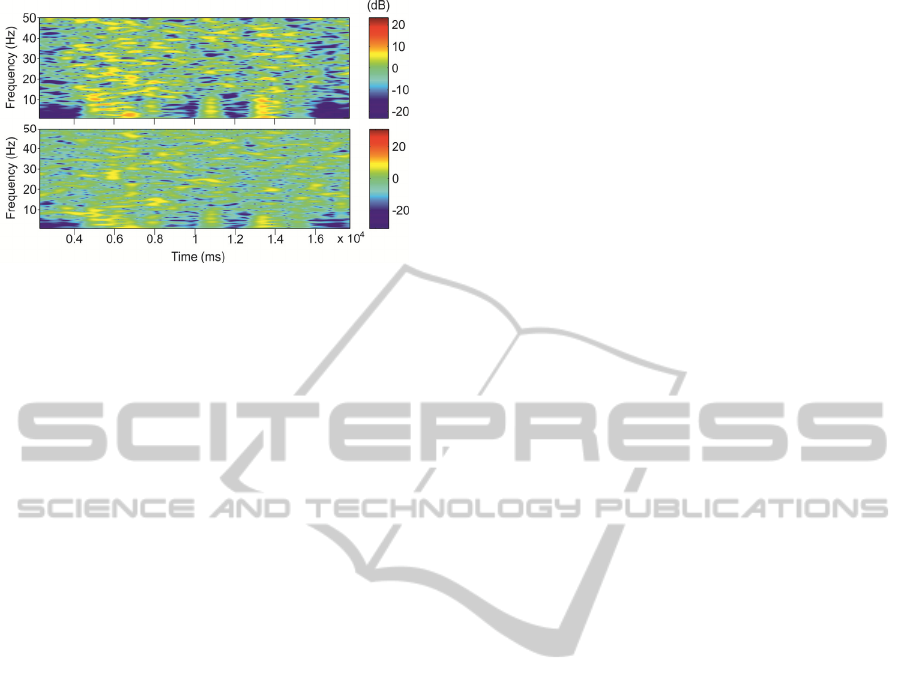
Figure 3: The time-frequency analysis for a noisy signal is

shown in the upper figure and for ANN output is shown in

the lower figure.

5 CONCLUSIONS

The present study demonstrates how ANN can be

used to reduce muscle noise in EEG data.

Throughout all stages, the ANN method was adapted

using the SP method, which was improved to

achieve our target. Our ANN method was shown to

be an effective enhancement tool. The techniques

proposed here can be applied in multichannel EEG.

In all of the practical cases studied, different kinds

of noise components appear in the recordings. For

this reason, the removal of noise facilitates the

clinical analysis for medical professional use.

As a way of conclusion, suffice is to say that the

ANN - based approach obtains both more signal

reduction and low distortion of the signal results in

comparison with traditional filtering techniques. The

results of this study show the maintenance of clinical

information. The technique which has been

proposing through this paper, finds its application by

means of denoising biological signals (EEG, ECG,

etc).

ACKNOWLEDGEMENTS

This work was sponsored by University of Castilla-

La Mancha (Spain) and Virgen de la Luz Hospital of

Cuenca (Spain).

REFERENCES

Bronzino, J., The Biomedical Engineering Handbook, 2nd

Ed, CRC Press, Springer, 2000.

Castellanos, N. P., Makarov,V. A., Recovering EEG brain

signals: Artifact suppression with wavelet enhanced

independent component analysis, J. Neuroscience.

Methods 158 (2006). 300–312.

Crespo-Garcia, M., Atienza M., Cantero, J., Muscle

artifact removal from human sleep eeg by using

independent component analysis, Annals Biomed Eng

36 (3) (2008) 467–475.

Haykin S., (1994) Neural Networks: A Comprehensive

Approach, IEEE Computer Society Press 1994,

Piscataway, USA.

Lagerlund, T, Sharbrough, F., Busacker N. Spatial

filtering of multichannel electroencephalographic

recordings through principal component analysis by

singular value decomposition, Brain Topography 17

(2) (2004) 73–84.

Maeda, Y., Hirano, H., Kanata, Y. A learning rule of

neural networks via simultaneous perturbation and its

hardware implementation, Neural Networks 8 (2)

(1995) 251–259.

Maeda, Y; Figueiredo, R. J. P. D., Learning rules for

neuro-controller via simultaneous perturbation, IEEE

Trans. on Neural Networks 8 (6) (1997) 1119–1130.

Olmos, S., Sörnmo, L. Laguna, P., Block adaptive filters

with deterministic reference inputs for event-related

signals: Blms and brls, IEEE Trans. Sign. Proces. 50

(5) (2002) 1102–1112.

Paul, J. S., Reddy, M. R., Kumar, V. J, A transform

domain SVD filter for suppression of muscle noise

artefacts in exercise ECG’s, IEEE Trans. Biomed.

Eng. 47 (5) (2000) 654–663

Rangayyan R., Biomedical Signal Analysis: A Case-Study

Approach, IEEE Press Series in Biomedical

Engineering, 2002.

Sameni, R; Shamsollahi, M.; Jutten, C. Model-based

bayesian filtering of cardiac contaminants from

biomedical recordings, Physiological Measurement 29

(5) (2008) 595–613.

Shao, S.-Y; Shen, K.-Q.; Ong, C. J.; Wilder-Smith, E. P.

V; Li, X.-P, Automatic eeg artifact removal: A

weighted support vector machine approach with error

correction, IEEE Trans. on Biomed. Eng. 56 (2)

(2009) 336–344.

Sörnmo, L. and Laguna, P., Bioelectrical Signal

Processing in Cardiac an Neurological Applications,

Elsevier Academic Press, 2005.

Spall, J. C. Multivariate stochastic approximation using a

simultaneous perturbation gradient approximation,

IEEE Trans. Automatic Control 37 (3) (1992) 332–

341.

Zhang, T; Okada, Y; Recursive artifact windowed-single

tone extraction method (raw-stem) as periodic noise

filter for electrophysiological signals with interfering

transients, J. Neuroscience Methods 155 (2) (2006)

308–318.

EEG NOISE CANCELLATION BASED ON NEURAL NETWORK

333