ESTIMATION OF IMPLICIT USER INFLUENCE

FROM PROXY LOGS

An Empirical Study on the Effects of Time Difference and Popularity

Tomonobu Ozaki

and Minoru Etho

1,2

Cybermedia Center, Osaka University, 1-32 Machikaneyama, Toyonaka, Osaka 560-0043, Japan

NTT DOCOMO R&D Center, 3-6 Hikarino-oka, Yokosuka, Kanagawa 239-8536, Japan

Keywords:

User inﬂuence, Proxy logs, Web usage mining.

Abstract:

In this paper, we propose a framework for estimating implicit user inﬂuence from proxy logs. For the esti-

mation, we employ a vector representation of user interactions obtained from log data by taking account of

popularity of web pages and difference of access time to them. One of the key issues for successful estimation

is how to model the popularity and time difference. Since appropriate models depend on application domains,

we propose various models of them. We conﬁrm the effectiveness of the proposed framework by conducting

experiments on web page recommendation and community discovery for real proxy logs.

1 INTRODUCTION

Browsing behavior of users on the web is inﬂuenced

implicitly and explicitly by others. Estimation of the

degree of user inﬂuence from log data is one of critical

tasks for wide variety of applications such as recom-

mendation, viral marketing and community discov-

ery. In this paper,we consider a problem of estimating

implicit user inﬂuence from proxy logs.

A user modeling from the aspect of interaction is

required to estimate user inﬂuence. We will explain

the necessity to model interactions by using a very

simple example. In the proxy log shown in Figure 1,

while three users

and

accessed to the web pages

A.html

and

B.html

in common, we can guess that the

degree of inﬂuence among them is not equal. While

always accesses the same web pages just after

’s

accesses, the access time of

is completely different

from those of

and

. Thus, we can easily expect that

the behavior of

gives signiﬁcant impact on that of

and the degree of inﬂuence of

is high. Besides

the difference of access time, popularity of web page

is a promising indicator of user interaction. Since all

users except

accessed to

A.html

in a short period

of time, we can judge that their browsing behaviors

A.html

might be caused by not user inﬂuence but

by global one. This very simple example shows that

taking account of page popularity and time difference

is one of key issues for accurate modeling of user in-

teraction and for estimation of user inﬂuence.

UID URL Time

x http://xxx/A.html 2011-04-01 10:01:40

y http://xxx/A.html 2011-04-01 10:02:21

z http://xxx/B.html 2011-04-01 10:02:48

m http://xxx/A.html 2011-04-01 10:08:06

n http://xxx/A.html 2011-04-01 10:10:15

··· ··· ···

x http://xxx/B.html 2011-04-01 15:12:59

y http://xxx/B.html 2011-04-01 15:14:01

··· ··· ···

z http://xxx/A.html 2011-04-01 20:09:10

··· ··· ···

Figure 1: An example of proxy log.

In this paper, we propose a model of user inter-

actions based on the page popularity and time dif-

ference, and develop methods for estimating implicit

user inﬂuence. In the area of social network analysis,

many sophisticated methods for estimating user inﬂu-

ence have been proposed, most of which assume link

formation representing user interactions. However,

we cannot always expect precise link information in

case of proxy logs. So, we prepare two methods for

the estimation: one does not require link information,

and the other works with additional (incomplete) in-

formation.

While we focus on the user inﬂuence in this paper,

the property of homophily(McPherson et al., 2001)

250

Ozaki T. and Etho M..

ESTIMATION OF IMPLICIT USER INFLUENCE FROM PROXY LOGS - An Empirical Study on the Effects of Time Difference and Popularity.

DOI: 10.5220/0003659702420247

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 242-247

ISBN: 978-989-8425-79-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

will also give signiﬁcant impact on user behavior. Ho-

mophily is the tendency of users to have similar be-

haviors with ones having similar characteristics. In

this paper, we drive a rough effect of homophily from

log data by using a simple model, and compare it with

the effect of inﬂuence. In addition, we consider the

mixture of homophily and inﬂuence.

The effectiveness of the proposed framework is

evaluated empirically by conducting experiments on

web page recommendation and community discovery.

2 MODELING THE DEGREE OF

INFLUENCE

A proxy log L consists of a set of triplets l = (u, p,t)

which indicates that a user u visited or accessed a web

page p at time t. We use notations U

= {u|(u, p,t) ∈

L } and P

= {p|(u, p,t) ∈ L } to denote a set of all

users and web pages in L , respectively.

Our purpose in this paper is to estimate the degree

of inﬂuence from a user x to other user y for every

ordered pair hx,yi ∈ U

× U

of users in L .

2.1 Representation of Interactions

For an ordered pair hx,yi of users, we employ an inter-

action vector to represent interactions from x to y on

each web page p (see Figure 2). The value of dimen-

sion p in an interaction vector is denoted as V

(p).

user pair p

··· p

i V

) ··· V

)

··· ··· ··· ···

i V

) ··· V

)

··· ··· ··· ···

|−1

i V

|−1

) ··· V

|−1

)

Figure 2: Vector representation of interactions.

To make V

(p) reﬂect signiﬁcance of interaction,

we formulate V

(p) in the exponential waiting time

model(Gomez Rodriguez et al., 2010) with the con-

sideration of importance of p. In the formulation, we

give high value to V

(p) if p is important and y’s ac-

cess time to p is close to that of x. In other words, we

regard that x affects y signiﬁcantly if y follows x’s be-

havior on important web pages. The formal deﬁnition

is given below:

(p) =











(p) · exp(−∆

(p)/α)

( min

(x,p,t

)∈L

) < min

(y,p,t

)∈L

))

0 (otherwise)

where α is a parameter, I

(p) denotes an importance

of p with respect to hx,yi, and ∆

(p) denotes a differ-

ence of timestamps when x and y visited p.

Various models of I

(p) and ∆

(p) in V

(p) can

be considered. In this paper, we examine four models

of I

(p) and two of ∆

(p).

The ﬁrst model of I

(p) is the inverse document

frequency (IDF) of p, deﬁned formally as:

idf(p) = log



|{z|(z, p,t

′

) ∈ L }|



In this setting, web pages accessed by fewer users

have higher importance.

The second model of I

(p) is restricted version of

IDF. Only triplets before y’s ﬁrst access to p are used

in calculating IDF.

r idf(y, p) = log





|{z|(z, p,t

′

) ∈ L ,t

′

≤ min

(y,p,t)∈L

(t)}|





r idf(y, p) reﬂects a context on p and y by consid-

ering the access time of y to p. It gives high value to

early adopters of p.

As the third model of I

(p), we consider the term

frequency - inverse document frequency (tf-idf) de-

ﬁned below. In this case, I

(p) depends on x and p.

tﬁdf(x, p) =

|{(x, p,t) ∈ L }|

|{(x, p

′

) ∈ L }|

× id f(p)

Finally, as the fourth model, we prepare a constant

function, i.e. I

(p) = 1.

Capturing the time difference on a web page p be-

tween two users x and y is not trivial since users visit

the same web pages several times. To reﬂect a situa-

tion in which y visits p by the inﬂuence of x, it is rea-

sonable to use the y’s ﬁrst access to p and x’s access

just before y’s ﬁrst access. On the other hand, if we

assume that x’s interest in p decreases with time and

thus x’s effect on p also decreases, using the ﬁrst ac-

cesses of y and x is another reasonable candidate. To

model the aboveideas, two models of time difference,

denoted as LtoF

(p) and FtoF

(p), are deﬁned:

LtoF

(p) = min

(y,p,t

)∈L

) − max

(x,p,t

)∈L

)

FtoF

(p) = min

(y,p,t

)∈L

) − min

(x,p,t

)∈L

)

where L

= {(z, p,t

) ∈ L |t

< min

(y,p,t

)∈L

)} rep-

resents a set of triplets in L whose time stamp is ear-

lier than y’s ﬁrst access to p.

2.2 Estimation of User Inﬂuence

For every ordered pair hx,yi of users, an interac-

tion vector can be obtained by instantiating I

(p) and

ESTIMATION OF IMPLICIT USER INFLUENCE FROM PROXY LOGS - An Empirical Study on the Effects of Time

Difference and Popularity

251

∆

(p) for all web pages p ∈ P

. Then, the vectors

will be used to estimate a user inﬂuence. In this paper,

we propose two methods for estimating user inﬂuence

from a set of interaction vectors.

The ﬁrst method is very simple. We estimate the

degree of inﬂuence from x to y, denoted as w

(x,y),

as the summation of elements in a vector on hx,yi:

(x,y) =

∑

p∈P

(p).

In addition, if necessary, we use a normalized inﬂu-

ence w

′

(x,y) = w

(x,y)/max

z∈U

(z,y)). As ex-

plained before, V

(p) indicates the degree of signiﬁ-

cance on the interaction from x to y on p. Thus, the es-

timation by summation gives high degree of inﬂuence

to hx,yi if there are many signiﬁcant interactions be-

tween two users. The idea behind this estimation is re-

lated to the traditional similarity measures which give

high similarity to the pair of vectors having manyhigh

value elements in common. In case of w

(x,y), the

information on “high value elements in common” be-

tween x and y is already encoded in calculatingV

(p)

since V

(p) reﬂects the signiﬁcance of interactions.

The second proposed method to estimate user in-

ﬂuences is application of supervised learning. While

it is difﬁcult to observe interactions and inﬂuences

directly in general, we prepare a class information

c : U

× U

→ {0,1} by using additional information

which indicates whether or not a user pair has a lot of

chances of interactions: c(x,y) = 1 means that there

is a high possibility of interaction and thus we regard

that x inﬂuences y signiﬁcantly, while c(x,y) = 0 cor-

responds to the opposite situation.

A model which estimates the probability that

c(x,y) = 1 can be obtained by applying a supervised

learning to a set of interaction vectors with class in-

formation, i.e.

{(hV

),··· ,V

)i, c(x,y) )|x, y ∈ U

We regard this probability as the degree of inﬂu-

ence from x to y and denote it as w

(x,y). Similar

to the case of w

, we use the normalized inﬂuence

′

(x,y) = w

(x,y)/max

z∈U

(z,y)) if necessary.

The property of homophily(McPherson et al.,

2001) also gives signiﬁcant impact on user behavior.

In this paper, we regard that the cosine similarity of

user behavior

(x,y) =

∑

p∈P

tﬁdf(x, p) · tﬁdf(y, p)

∑

p∈P

tﬁdf(x, p)

∑

p∈P

tﬁdf(y, p)

roughly represents homophily effects and use it as a

baseline method. In addition, we consider a mixture

of homophily and inﬂuence:

(x,y) = λ

(x,y)

max

z∈U

(z,y))

+ (1 − λ)w

′

(x,y)

where λ is a mixture parameter and I ∈ {σ,L}.

3 EXPERIMENTS

The proposed framework is evaluated by tasks of web

page recommendation and community discovery.

3.1 Datasets

After the application of standard data cleaning, three

datasets L

, L

and L

are prepared from a proxy

server log recorded in Osaka University from April

to June 2010. In addition, as a simple abstraction for

better estimation, all parameters in URL (string after

“?”) are deleted.

: It contains about 308,000 records of 99 students

who belong to a certain department on sciences.

: It contains about 258,000 records of 151 students

who belong to a certain department on arts.

: It contains about 242,000 records of 157 students

participating in a certain project.

We prepare class information for L

and L

based

on the physical location of computers determined by

IP address recorded in the original proxy log. We

judge c(x, y) = 1 if there exists at least one situation in

which two students x and y use two computers located

adjacent to each other at the same time. As a result,

the numbers of user pairs hx,yi judged as c(x,y) = 1

become 786 in L

and 776 in L

, respectively. We

prepare class information for L

by using ‘group in-

formation’ obtained by a questionnaire. The students

in L

consists of six groups having 50, 50, 26, 13, 10,

and 8 members, respectively. We judge c(x,y) = 1 if

x and y belong to the same group.

3.2 Web Page Recommendation

3.2.1 Estimation of User Inﬂuence

We prepare six settings on α for the exponential wait-

ing time model, denotes as D

, D

, H

150

and H

300

, respectively. In case of D

(a= {5,10, 20}),

we abstract timestamps at the level of “day” and set

the parameter α to a. On the other hand, H

(a =

{75, 150, 300}) denotes the abstraction of timestamps

at the level of “hour”. While D

corresponds to the

situation in which the effect of page importance de-

creases to about 0.5 in a week, H

150

cuts down the

effect to about 0.3 in the same period.

By considering all the combinations of I

(p),

∆

(p) and α, 48(= 4× 2 × 6) sets of interaction vec-

tors are obtained for each datasets. From each set

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

252

Table 1: Number of records for web page recommendation.

i,1

| |A

i,1

| |P

i,2

| |A

i,2

i = 1 38,827 140,421 104,221 88,303

i = 2 25,347 35,079 21,367 38,663

i = 3 25,962 61,432 30,171 67,276

of interaction vectors, we derive w

by summation

and w

by supervised learning of LibSVM(Chang and

Lin, 2001). Parameters for SVM learning were deter-

mined by the grid search. We employ w

as a base-

line. The mixtures w

and w

are also obtained by

setting λ = 0, 0.05, 0.1,· ·· ,0.95, 1, respectively.

3.2.2 Evaluation Metrics

For each L

(i = {1, 2,3}), two pairs of datasets L

i, j

)( j = {1,2}) are prepared from the same

proxy server log recorded in July 2010. While P

i, j

is a set of records of students in L

for one week, A

i, j

is a set of records for two weeks just after P

i, j

. P

i, j

and

i, j

are used for producing a recommendation set and

an answer set, respectively. Different from L

, we do

not apply the abstraction of URL to L

i, j

. The numbers

of records are summarized in Table 1.

For each user x, a set of web pages to which x does

not access in P

i, j

is produced as a recommendation set

i, j

(x) = {p|(z, p,t) ∈ P

i, j

,z 6= x} \ {p|(x, p,t) ∈ P

i, j

Each web page p in the recommendation set has the

score v(p, x) =

∑

z∈{z6=x| (z,p,t)∈P

i, j

}

w(z,x) of weighted

voting according to a user inﬂuence w. We sort P

i, j

(x)

in descending order of the scores. On the other hand,

we deﬁne the answer set as

i, j

(x) = {p|(x, p,t) ∈ A

i, j

,(x, p,t

′

) 6∈ P

i, j

} ∩ P

i, j

(x).

We believe that recommendation of minor web

pages is worth more than that of major ones. To re-

ﬂect such consideration, we put a weight w(p) on a

web page p based on inverse document frequency, i.e.

w(p) = log



i, j

|/|{z|(z, p,t

′

) ∈ P

i, j



We employ the macro average of weighted pre-

cision@k taken over users as an evaluation criterion.

The weighted precision@k for a user x is deﬁned as :

p@k(x) =

∑

p∈P

i, j

(x)

I(x, p, k) · w(p) /

∑

p∈P

i, j

(x)

w(p)

where I(x, p, k) is an indicator function which be-

comes 1 if p is in A

i, j

(x) and it also locates within

the k-th place in P

i, j

(x). Otherwise, I(x, p,k) = 0.

As another evaluation criterion, mean average pre-

cision (MAP) is employed:

MAP =

i, j

∑

x∈U

i, j

∑

p∈A

i, j

(x)

p@k(x, p)(x)

where k(x, p) is the rank of p in P

i, j

(x).

3.2.3 Results

Table 2 shows the best values of MAP among all the

combinations of parameters. The best values within

each L

i, j

are marked by underline. We can observe

that the proposed methods outperform the baseline

). In addition, the mixtures of homophily and in-

ﬂuence (w

and w

) take the ﬁrst place in all cases.

In comparison with the results by summation (w

and

), results by supervised learning (w

and w

) are

better in all cases of L

3, j

. On the other hand, such

tendency is not recognized in L

1, j

and L

2, j

Table 2: Best values of MAP.

MAP L

1,1

1,2

2,1

2,2

3,1

3,2

0.231 0.162 0.167 0.269 0.210 0.293

0.250 0.198 0.191 0.299 0.240 0.308

0.253 0.191 0.166 0.303 0.242 0.311

0.260 0.198 0.194 0.306 0.243 0.321

0.260 0.194 0.170 0.310 0.253 0.330

We show the average values of MAP and preci-

sion@k (k = {5,10}) for w

and w

taken over 48

combinations of parameters in Table 3. In the table,

all average MAP values except w

for L

2,1

and w

for L

3,2

outperform those of baseline method. Simi-

lar to MAP, average values of precision@k tend to be

higher than corresponding values of baseline method.

While w

is clearly better than w

in L

2,2

, L

3,1

and

3,2

, w

is worse in others, especially in L

2,1

From the results, we simply conclude that: (1)the

proposed methods perform well under appropriate pa-

rameter settings, (2)the mixture of homophily and

inﬂuence gains the result of recommendation, and

(3)the quality of class information has an impact on

user inﬂuence obtained by supervised learning.

Table 3: Average values of MAP and precision@k.

MAP L

1,1

1,2

2,1

2,2

3,1

3,2

0.231 0.162 0.167 0.269 0.210 0.293

0.241 0.180 0.173 0.281 0.218 0.287

0.245 0.188 0.157 0.299 0.235 0.305

precision@5

0.436 0.337 0.152 0.343 0.310 0.387

0.440 0.369 0.162 0.348 0.334 0.385

0.422 0.358 0.111 0.357 0.342 0.410

precision@10

0.310 0.230 0.134 0.219 0.246 0.310

0.347 0.251 0.150 0.239 0.262 0.307

0.348 0.233 0.124 0.250 0.271 0.339

In order to assess the effects of parameters, we

compare the MAP values in all datasets obtained by

different models of page importance I

(p) under the

ESTIMATION OF IMPLICIT USER INFLUENCE FROM PROXY LOGS - An Empirical Study on the Effects of Time

Difference and Popularity

253

same settings other than I

(p). For each proposed

methods w

and w

, we have 72 comparisons in to-

tal because of two of time differences, six of αs and

six of datasets. The ratio of taking the best value is

summarized in Table 4. We apply the same compar-

isons to ∆

(p) and α. The results on ∆

(p) and α are

obtained from 144 and 48 comparisons, respectively.

While tﬁdf and const drive better results in w

, r idf is

the best in w

. H

300

clearly outperforms others in w

LtoF is better than FtoF in both w

and w

. Since the

winning rates are not uniform, we can recognize that

different models givesigniﬁcant impact on the results.

Table 4: Winning rates of different models in MAP.

idf 0.153 0.139 D

0.000 0.083

r idf 0.125 0.347 D

0.063 0.083

tﬁdf 0.347 0.181 D

0.313 0.250

const 0.375 0.333 H

0.104 0.229

FtoF 0.222 0.333 H

150

0.104 0.146

LtoF 0.778 0.667 H

300

0.417 0.208

A similar analysis is also applied to a mixture pa-

rameter λ in w

and w

. The results are shown in

Figure 3. The value of λ between 0.5 and 0.55 and

that between 0.65 and 0.75 seem to be promising for

and w

, respectively. Compared with w

, the peak

of w

exists at the higher value of λ. In other words,

requires large effect of homophily to get better re-

sults on web page recommendation. We believe that

unreliability of class information of L

and L

causes

these results.

0.05

0.1

0.15

0.2

0.7

0.05

0.1

0.15

0.2

0.7

Figure 3: Winning rates of different λs in MAP.

3.3 Community Discovery

We conduct experiments on community discovery by

using the dataset L

As the same as the experiments on web page rec-

ommendation, we prepare 48 of w

s for each combi-

nation of parameters. On the other hand, we employ

a cross-validation like method to derive w

. In the

method, a set of interaction vectors is divided into ﬁve

pieces and the inﬂuence w

(x,y) in one piece is esti-

mate by using a model build from other four pieces.

A community structure having maximal modular-

ity(Newman and Girvan, 2004) is discovered by us-

ing the igraph library(Csardi and Nepusz, 2006). By

using the group information obtained by a question-

naire as a correct answer, we evaluate the discovered

community structure based on normalized mutual in-

formation (NMI)(Danon et al., 2005). The range of

NMI is from 0 to 1, and high value indicates that the

predicted structure is similar to the answer.

The best and average values of NMI over all the

combinations of parameters are shown in Table 5. In

the results, we observe that the proposed methods out-

perform the baseline method w

. Especially, the best

value of w

is signiﬁcant. But it is not surprising since

we use class information to prepare w

even if a cross-

validation like method is applied. Different from the

results in web page recommendation, the mixtures w

and w

become worse than w

and w

. We believe

that the normalization process causes these results. In

fact, the best values of NMI in the normalized inﬂu-

ences w

′

and w

′

are 0.145 and 0.217, respectively.

Table 5: Best and average values of NMI.

Best 0.150 0.227 0.150 0.426 0.235

Avg. 0.150 0.165 0.127 0.266 0.156

The effects of parameters are assessed in Table 6.

In the table, FtoF drives better results in w

and H

signiﬁcantly outperforms others in w

and w

. While

and w

have the same tendency on ∆

(p) and α,

the results on I

(p) is quite different between them.

Table 6: Winning rates of different models in NMI.

idf 0.000 0.083 D

0.000 0.000

r idf 0.000 0.333 D

0.000 0.188

tﬁdf 0.750 0.000 D

0.000 0.000

const 0.250 0.583 H

0.875 0.500

FtoF 0.521 0.667 H

150

0.125 0.250

LtoF 0.479 0.333 H

300

0.000 0.063

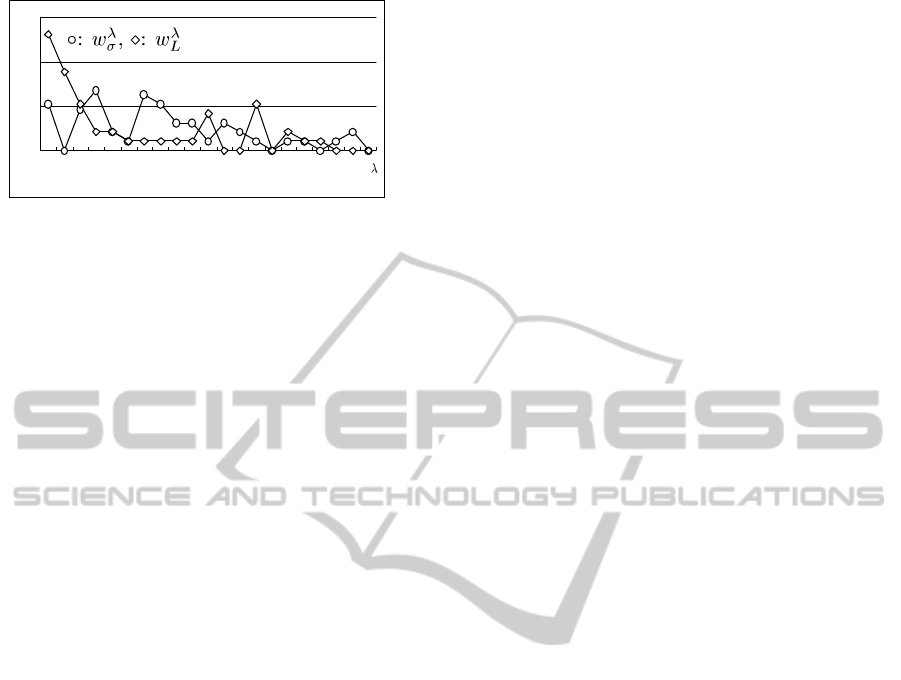
Figure 4 shows the results of comparisons on a

mixture parameter λ. We can observe that small λs

get better results in w

due to the supervised learn-

ing. The peak of w

is also small relatively. These

results suggests that the effect of inﬂuence is domi-

nant than that of homophily on community discovery

in this dataset.

The parameter effects are completely different

from the tasks of web page recommendation and that

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

254

0.1

0.2

0.3

0.1

0.2

0.8

0.1

0.2

0.3

0.1

0.2

0.8

Figure 4: Winning rates of different λs in NMI.

of community discovery. Thus, we can conﬁrm that

the appropriate parameter setting heavily depends on

application domain.

4 RELATED WORK

Estimation of user inﬂuence attracts much attention

in the area of social network analysis, and many so-

phisticated models are proposed, e.g. (Goyal et al.,

2010; Kimura et al., 2009). However, it is difﬁcult to

apply them directly to proxy logs not having precise

information to construct accurate user networks.

Several methods for estimating user inﬂuence

without explicit network information have been de-

veloped recently. In (Gomez Rodriguez et al., 2010),

an algorithm named ‘netinf’ is proposed which esti-

mates hidden network structures from a set of infor-

mation cascades obtained from (proxy) log data. Net-

inf estimates directed unweighted networks of users

by adopting the exponential waiting time model on

information diffusion while it assumes that the de-

gree of user inﬂuences are the same among any user

pairs. As an extension of netinf, a convex program-

ming based method for inferring directed weighted

network structures from cascade data has been pro-

posed in (Myers and Leskovec, 2010). While these

two methods employ the exponential waiting time

model for reﬂecting information on time difference,

they do not consider the importance of contents at all.

A probabilistic model for user adoption behaviors

has been proposed in (Au Yeung and Iwata, 2010).

By using the model, user inﬂuence as well as inﬂu-

ences of popularity and recency of contents are esti-

mated from log data. The model requires a parameter

specifying the length of period in which a user affects

others. In other words, behaviors outside of the pe-

riod are regarded to give no effect. On the other hand,

the effects of behaviors decrease gradually with time

in our proposal.

5 CONCLUSIONS

In this paper, we propose a framework for estimat-

ing implicit user inﬂuence from proxy logs. We

model user interactions as vectors by taking account

of the difference of access time and importance of

web pages, and use the vectors to estimate the inﬂu-

ence. The proposed methods are evaluated empiri-

cally by using three real datasets in the tasks of web

page recommendation and community discovery.

For future work, detailed assessments of obtained

user inﬂuences are necessary. In addition, we plan to

investigate further experiments with large-scale proxy

logs having different characteristics as well as pre-

cise comparisons with related techniques on estimat-

ing user inﬂuence.

REFERENCES

Au Yeung, C.-m. and Iwata, T. (2010). Capturing implicit

user inﬂuence in online social sharing. In Proceedings

of the 21st ACM Conference on Hypertext and Hyper-

media, pages 245–254.

Chang, C.-C. and Lin, C.-J. (2001). LIBSVM: a library

for support vector machines. Software available at

http://www.csie.ntu.edu.tw/˜cjlin/libsvm

Csardi, G. and Nepusz, T. (2006). The igraph software

package for complex network research. InterJournal,

Complex Systems:1695.

Danon, L., D´ıaz-Guilera, A., Duch, J., and Arenas, A.

(2005). Comparing community structure identiﬁca-

tion. Journal of Statistical Mechanics: Theory and

Experiment, 2005(9):P09008.

Gomez Rodriguez, M., Leskovec, J., and Krause, A. (2010).

Inferring networks of diffusion and inﬂuence. In

Proceedings of the 16th ACM SIGKDD International

Conference on Knowledge Discovery and Data Min-

ing, pages 1019–1028.

Goyal, A., Bonchi, F., and Lakshmanan, L. V. (2010).

Learning inﬂuence probabilities in social networks. In

Proceedings of the third ACM International Confer-

ence on Web Search and Data Mining, pages 241–250.

Kimura, M., Saito, K., and Motoda, H. (2009). Efﬁcient

estimation of inﬂuence functions for sis model on so-

cial networks. In Proceedings of the 21st International

Joint Conference Artiﬁcial Intelligence, pages 2046–

2051.

McPherson, M., Lovin, L. S., and Cook, J. M. (2001). Birds

of a Feather: Homophily in Social Networks. Annual

Review of Sociology, 27(1):415–444.

Myers, S. and Leskovec, J. (2010). On the convexity of

latent social network inference. In Advances in Neu-

ral Information Processing Systems 23, NIPS, pages

1741–1749.

Newman, M. E. J. and Girvan, M. (2004). Finding and eval-

uating community structure in networks. Physical Re-

view E, 69(2):026113.

ESTIMATION OF IMPLICIT USER INFLUENCE FROM PROXY LOGS - An Empirical Study on the Effects of Time

Difference and Popularity

255