
AN APPLICATION OF SEMANTIC DISTANCE BETWEEN SHORT
TEXTS TO INVENTIVE DESIGN
Wei Yan
1
, Cecilia Zanni-Merk
2
and Francois Rousselot
2
1
LGECO/INSA de Strasbourg, 24 Boulevard de la Victoire, Strasbourg Cedex, France
2
LSIIT/BFO Team, UMR CNRS 7005, P
ˆ
ole API, BP 10413, Illkirch Cedex, France
Keywords:
Semantic distance, Information content, WordNet, Inventive design.
Abstract:
The gradual development of inventive design techniques makes that numerous knowledge sources are available
for experts to solve inventive problems in different technical and non-technical fields. Real-world problems
are established in terms of parameters that are inherent to the artefact being developed, but inventive design
techniques use generalized engineering parameters to propose solutions to the problem. An abstraction effort
needs to be provided to choose, then, the best generalized parameter. In this paper, we firstly present the
inventive principles ontology we have established as a support for our approach. According to this ontology,
we propose a method to calculate the semantic distance between short texts and use it to fill the semantic gap
between the parameter and the generalized one, to facilitate the use of inventive design techniques.
1 INTRODUCTION
The inventive design methodology we are interested
in, TRIZ (Theory of Inventive Problem Solving) (Alt-
sthuller, 1984) (Altsthuller, 1999), is primarily about
technical and physical problems, but is now being
used on almost any problem or situation. The key to
success in TRIZ is the fact that (technical) systems
evolve in similar ways, and, by reducing any situa-
tion and problem to a functional level, we can apply
almost standard solutions and problem solving tech-
niques, even from dissimilar industries.
The creator of TRIZ, the Russian engineer Gen-
rich Altshuller proved that a systematic approach to
the inventive process is possible. A major conclusion
of Altshuller’s studies was that inventions were not a
result of unorganized thinking, but instead the prod-
ucts of objective laws and trends of technology evolu-
tion.
Comprehensive studies of patent collections fol-
lowing this discovery resulted in two more findings.
First, Altshuller shows that an inventive solution re-
sults from the elimination of a contradiction which is
caused by attempts to improve preceding design prod-
ucts. Attempts to compromise without eliminating
the contradiction do not allow a designer to achieve
the desired degree of improvement. The second con-
clusion is that the majority of the patented inventions
comply with a relatively small set of basic principles
for eliminating the contradictions. Based on these
findings, Altshuller has developed a scientifically-
based problem solving methodology which codifies
numerous inventive principles and incorporates the
laws of engineering system evolution.
There are several disadvantages in the direct use
of classical TRIZ, as it has not been fully formalized:
• The wealth of knowledge available in TRIZ is
necessary for solving a large variety of inventive
problems but access to the needed specific knowl-
edge might be troublesome.
• TRIZ does not operate with formal scientific cat-
egories, thus making impossible the application
of quantitative constraints at the phase of problem
formulation, although, it is often the case.
• TRIZ definitions of physical concepts such as sub-
stances and fields are ambiguous and can not be
adequately interpreted.
• Using a recommendation proposed by TRIZ for
solving a specific problem requires an extensive
knowledge of different engineering domains and
is not currently supported. Therefore, the user is
supposed to have a high degree of expertise in en-
gineering design (Cavallucci and Eltzer, 2007).
We make the hypothesis that semantic technolo-
gies may be used to fill the gap between real-world
problems and the high level abstract concepts manip-
261
Yan W., Zanni-Merk C. and Rousselot F..
AN APPLICATION OF SEMANTIC DISTANCE BETWEEN SHORT TEXTS TO INVENTIVE DESIGN.
DOI: 10.5220/0003660702610266
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2011), pages 261-266
ISBN: 978-989-8425-80-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

ulated by TRIZ. We therefore present here, in section
2, a short introduction to TRIZ with the explicitation
of the problem we intend to solve. In section 3 we
present the ontology we have established as a support
for our development. Section 4 presents our proposal
for a solution, and in particular, after a short state of
the art on the measurement of semantic distance, we
present the one we have retained. Experiments val-
idating our approach are presented in section 5 and,
finally, section 6 presents some conclusions and per-
spectives of future work.
2 INTRODUCTION TO TRIZ
A goal of the design process is to map a function onto
a physical principle that would be capable of perform-
ing the function. But what can be done in a situation
when an exact function to be performed is not avail-
able? Or, none of the previous solutions meet the new
specifications? Inventive design is difficult to perform
due to the uncertainty on how an original problem can
be translated into the functional specifications.
From this point of view, the most important TRIZ
achievement was that it reveals the common cause
of inventive design problems: contradictions (Alt-
sthuller, 1984). A contradiction arises from mutually
exclusive demands that may be placed on the same
system where compromising does not produce the re-
quired result. Instead of solving inventive problems
ad-hoc, TRIZ introduces principles for the formula-
tion and elimination of the contradictions in a system-
atic way.
2.1 Types of Contradictions
Altshuller proposed to formulate inventive problems
in terms of contradictions with respect to already ex-
isting design.
Two types of contradictions are known in TRIZ:
technical and physical (in our case, we will only be
concerned by technical conradictions). The techni-
cal contradiction arises when it is required to improve
some feature of the existing artefact but all solutions
known within the domain do not produce the required
result or their use would cause a negative effect. The
impossibility to improve one parameter and to prevent
another important parameter from deterioration is the
main feature which separates inventive problems from
problems that can be solved by a procedure of routine
design.
Example of a Technical Contradiction: Structures
that have to be both strong and light. Strength im-
proves by adding more material, which makes weight
worse and vice versa.
2.2 Inventive Principles for Elimination
of Technical Contradictions
The first TRIZ problem solving technique was a col-
lection of Inventive Principles aimed at eliminating
technical contradictions. They are heuristic principles
based on the accumulated and generalized previous
experience of inventors and are available in a form
that is independent of any particular engineering do-
main.
To make the inventive principles applicable in a
systematic way, Altshuller formulated 39 generalized
engineering parameters, like ”the weight of a movable
object” or ”speed”.
A new problem can be solved by the use of a
proper inventive principle, after the problem has been
formulated as a technical contradiction in terms of
predefined generalized parameters: ”a generalized pa-
rameter to be improved versus a generalized param-
eter which deteriorates”. Forty Inventive Principles
aimed at resolving contradictions between general-
ized parameters are known.
The inventive principles can be used in a system-
atic way by accessing the principles through indices
in a matrix. Along the vertical axis of this matrix the
generalized parameters which have to be improved
are specified. Along the horizontal axis the param-
eters which deteriorate as a result of the improve-
ment are specified. These parameters can be looked
up along the vertical and horizontal axes and the ma-
trix suggests up to four principles that can be used to
solve the contradiction.
Selected principles are ordered according to their
applicability. The principle that will most likely solve
the problem is given first.
Example
1
- Improving the strength of an ob-
ject (the improvement feature) which consequentially
gives rise to an undesirable conflict with the ease
of manufacture of the object. The matrix suggests
4 principles: 11-Beforehand compensation, 3-Local
quality, 10-Preliminary action, 32-Optical changes.
In changing an object such as a garden spade to resist
breaking during use, we may add more process steps
in manufacture or use a material that is more difficult
to work. To counter this, we can use the same ma-
terial or process, but change the object to make it in-
herently stronger. Replaceable handles and localized
hardening help deal with strength issues, whereas pre-
assembled parts and color coded assembly deal with
manufacturing process issues. A handle that changed
1
Adapted from (Tennant, 2003).
KEOD 2011 - International Conference on Knowledge Engineering and Ontology Development
262

color when stressed too much would alert the user be-
fore the spade broke.
2.3 The Problem
If we consider the last example, the contradiction is
already established in terms of Altshuller’s general-
ized parameters (strength needs to be improved, but
in that case, ease of manufacturing degrades).
In real-world problems, the contradictions are es-
tablished in terms of parameters that are inherent to
the artefact being developed, and there is a semantic
gap to fill between those parameters and the general-
ized ones. An abstraction effort needs to be provided
to choose the best generalized parameter, and in this
way, be able to use the contradiction matrix.
Example: In the framework of an inventive design
project proposed to a class of engineering students in
our school, there was the study of the improvement
of a barbecue grill. The students have retained to fol-
lowing contradiction to solve: if the number of parts
in the wire mesh is high, the mastery of the beef done-
ness is satisfying but the weight of the grill is unsat-
isfying. On the other hand, if the number of parts is
low, the mastery of the beef doneness is unsatisfying
but the weight is satisfying. We have then two param-
eters: PE1, the weight; PE2; the mastery of the beef
doneness.
PE1 is directly associated with the 2nd general-
ized parameter ”weight of a stationary object”; but
for PE2, the association with the 35th generalized pa-
rameter ”adaptability or versatility” is not intuitive.
TRIZ uses 40 principles and sometimes they are
declined in sub-principles. In the following, we have
decided to use only sub-principles in order to have a
uniform granularity.
3 THE INVENTIVE PRINCIPLES
ONTOLOGY
The Contradiction Matrix consists in 39 Features (or
Generalized Parameters) and 40 Inventive Principles,
and each two Features correspond to an Item: one
acts as positive feature, the other as negative feature.
Each Item can have i Inventive Principles (i = 0 ···n),
and each Inventive Principle can have i Sub Inventive
Principles (i = 0·· ·n).
Each Feature refers to two concepts: Primary
Feature (1 : 1) - the initial description of Feature, such
as ’power’; Applied Feature (1 : i, i = 0··· n) - the de-
tailed description of the application, such as ’electri-
cal energy’.
Each Sub Inventive Principlealso refers to two
concepts: Primary Sub Inventive Principle (1 : 1) -
the initial description of the Sub Inventive Principle,
such as ’IP38a- replace normal air with air’; Applied
Sub Inventive Principle (1 : i, i = 0 ···n) - the detailed
solution of the application, such as ’replace normal air
with ozone’.
The semantic links of Applied Feature, Primary
Sub Inventive Principle and Applied Sub Inventive
Principle are depicted by an objectProperty linksWith
in the inventive principles ontology.
In order to solve inventive problems based on the
inventive principles ontology, we create a instance of
the Applied Feature, manually connect it to the cor-
responding Primary Feature, and then use the Con-
tradiction Matrix to look for the Inventive Principle,
the Sub Inventive Principle and the Primary Sub In-
ventive Principle. Finally, we obtain ideas from the
Primary Sub Inventive Principle and establish our de-
tailed Applied Sub Inventive Principle.
In the process stated above, the accuracy of the
traditional TRIZ solving process depends on the sub-
processes from Applied Feature to Primary Feature,
from Primary Sub Inventive Principle to Applied Sub
Inventive Principle, which need to be implemented
manually and require a large amount of TRIZ and do-
main knowledge.
We are interested in trying to automate, as much
as possible, this process.
4 OUR PROPOSAL
In this section,we present our proposal of a framework
to help experts in the search for similar inventions in
related or non-related fields.
4.1 The Semantic Similarity Calculation
The literature presents several surveys on measures
of semantic relatedness, in particular, (Budanitsky,
1999) presents an extensive state of the art and
classification. We are interested in the measures
that use WordNet (Fellbaum, 1998) as a knowledge-
base. These methods vary from simple edge-counting
(Rada et al., 1989) to attempts to calculate taking
into account certain characteristics of the structure of
WordNet by considering the link direction (Fellbaum,
1998), the relative depth (Sussna, 1993) or the density
(Agirre and Rigau, 1996). There are also other meth-
ods using statistical and machine learning techniques.
Finally, there are hybrid approaches combining dif-
ferent knowledge sources ((Resnik, 1995), (Jiang and
Conrath, 1997) or (Lin, 1998)).
AN APPLICATION OF SEMANTIC DISTANCE BETWEEN SHORT TEXTS TO INVENTIVE DESIGN
263

Resnik’s (Resnik, 1995) approach is based on the
fact that the similarity between a pair of concepts may
be measured by ”the extent to which they share infor-
mation”. Similarity between two concepts in Word-
Net is defined as the information content of their low-
est super-ordinate or most specific common subsumer
lso(c1, c2):
sim
R
(c1, c2) = −log(p(lso(c1, c2)) (1)
where p(c) is the probability of encountering an in-
stance c of a set of synonyms in some specific corpus.
Jiang and Conrath (Jiang and Conrath, 1997) also
use the notion of information content, but in the form
of the conditional probability of encountering an in-
stance of a child set of synonyms given an instance
of a parent set of synonyms. Therefore, the informa-
tion content of the two concepts and that of their most
specific subsumer play a role in this distance.
dist
JC
(c1, c2) = 2 ∗ log(p(lso(c1, c2)))
−log(p(c1)) −log(p(c2))
(2)
In the end, Lin (Lin, 1998) measures similarity
with the same elements as Jiang and Conrath, but used
in a different way.
sim
L
(c1, c2) =
2 ∗ log(p(lso(c1, c2)))
log(p(c1))+ log(p(c2))
(3)
In our proposal, the information content (IC) we
use is:
IC(c) = 1 −
log(hypo(c)+ 1)
log(max
wn
)
(4)
where c represents a concept, hypo(c) returns the
number of hyponym concepts of concept c in Word-
Net, and max
wn
is the number of concepts in Word-
Net.
In the framework we are considering, we usu-
ally need to calculate the semantic similarity between
short texts, such as the text description of the inven-
tive principles or features. Therefore, we present here
a specific method to calculate semantic similarity be-
tween short texts, which includes the following five
steps:
1. Word Segmentation: We need to divide the
short text into several words by using tech-
niques of word segmentation, such as tokeniza-
tion (e.g., substance appearance - disappearance
→ <substance, appearance, disappearance>),
lemmatization (i.e., copies → copy) and elimina-
tion (e.g., remove ’a’, ’by’, ’my, ’to’) (Rahm and
Bernstein, 2001).
Figure 1: The framework of the new version of the ontology.
2. Sense Search: For each word obtained, we use
WordNet to look for their corresponding senses,
including nouns, verbs, adjectives and adverbs.
For example, the noun form of the word ’way’ has
12 senses.
3. Sense Similarity: We use Lin’s measure (Lin,
1998) to calculate the semantic similarity of the
senses of two words. With this measure, it is obvi-
ous that in WordNet, the higher the rate of sharing
information, the more similar two concepts.
4. Word Similarity: We choose the maximum sense
similarity of two words as their word similarity.
5. Short Text Similarity: Short text similarity is
calculated based on word similarity. We as-
sume that two sentences: A, including words se-
quence A
1
, A
2
···A
m
and B, including B
1
, B
2
···B
n
.
s(A
i
, B
j
) represents word similarity of A
i
and B
j
,
1 6 i 6 m, 1 6 j 6 n. We can build the matrix
M(A, B):
s(A
1
, B
1
) s(A
1
, B
2
) ··· s(A
1
, B
n
)
···
s(A
i
, B
1
) s(A
i
, B
2
) ··· s(A
i
, B
n
)
···
s(A
m
, B
1
) s(A
m
, B
2
) ··· s(A
m
, B
n
)
(5)
We can use this matrix to obtain the semantic sim-
ilarity of two sentences A and B:
s(A, B) =
∑
m
i=1
max(s(A
i
, B
1
), ··· , s(A
i
, B
n
))
m
(6)
4.2 The Use of the Contradiction Matrix
based on Semantic Similarity
For each new problem, we identify then the parame-
ters involved in the contradiction to solve. Semantic
KEOD 2011 - International Conference on Knowledge Engineering and Ontology Development
264

matching is done to find the most accurate generalized
parameters. Once the generalized parameters are
identified, we are able to search, in the existing prob-
lems base, the ones that used the same generalized pa-
rameter and identify the inventive principle and sub-
principle used and in which way they were applied.
These data will provide the users with ideas of appli-
cation of the inventive principles that may be appro-
priate for their needs.
4.3 The New Version of the Ontology
To support the methodology outlined in the previous
subsection, we have modified the initial ontology to
add the concept of Problem (Fig. 1).
According to this new ontology framework, we
create instances for inventions available, at the same
time, we establish semantic links among inventions.
Firstly, for each problem, we build instances of the
Problem, the Applied Feature, the Applied Sub Inven-
tive Principle and establish links between the Applied
Feature and the Primary Feature, the Applied Sub In-
ventive Principle and the Primary Sub Inventive Prin-
ciple.
Next we search for semantic links according to the
comparison between semantic similarity of the Ap-
plied Feature, the Primary Sub Inventive Principle
and the Applied Sub Inventive Principle and pre-fixed
threshold
1
(for Applied Feature), threshold
2
(for Ap-
plied Sub Inventive Principle) and threshold
3
(for
Primary Sub Inventive Principle).
We set f lag to indicate whether a semantic link
is found, that is, 0-not found, 1-found. According to
estimating the value of f lag, we finish our program
only when we find the first similar problem, which
avoids to overlap of the semantic links to be built.
The pseudo-code for the automatic instantiation of
the inventive principles ontology is shown here:
Begin
Input: The framework of the inventive princip-
les ontology, problems,
threshold
1
, threshold
2
, threshold
3
Output: The instantiated inventive principles
ontology with all the semantic links
// F-Feature, PF-PrimaryFeature, AF-AppliedFe-
ature, IP-InventivePrinciple, SIP-SubInven-
tivePrinciple, PSIP-PrimarySubInventivePri-
nciple, ASIP-AppliedSubInventivePrinciple,
P-Problem;
1. According to contradiction matrix, create
39 F instances f and 39 corresponding PF
instances p f , 40 IP instances ip and
their corresponding SIP instances sip,
PSIP instances psip;
2. For each problem
a. Create a P instance p;
b. Create its AF instance a f , and connect
to its corresponding f and p f ;
c. Create its ASIP instance asip, connect
to its corresponding psip, sip, and ip.
d. If there is no existing problem instance
return;
EndIf
Else
int f lag=0;
// f lag indicates whether semantic
links are found(0 − No, 1 −Yes);
For each existing problem instance p
i
If Similarity(a f ,a f
i
)≥ threshold
1
// Similarity(s1, s2) returns the
semantic similarity between two sent-
ences s1 and s2;
linksWith(a f ) = a f
i
;
// linksWith is a objectProperty connec-
ting two concepts in ontology;
f lag++;
EndIf
If Similarity(asip,asip
i
)≥ threshold
2
linksWith(asip) = asip
i
;
f lag++;
EndIf
If Similarity(psip, psip
i
)≥ threshold
3
linksWith(psip) = psip
i
;
f lag++;
EndIf
If f lag 6= 0
Succeed in building semantic links.
EndIf
EndFor
If f lag = 0
Fail in building semantic links.
EndIf
EndElse
EndFor
End
5 EXPERIMENTS
To test our approach, we have analyzed a set of
projects proposed to engineering students of our
school. The students needed to solve an inventive
project (such as an improvement of existing artifacts).
Our experiments have been developed in a Java 2
platform, WordNet 2.0 and JWNL13rc3 (Java Word-
Net Library) on a Windows environment, taking ten
inventive problems as examples.
For each problem, we consider the two features in-
tervening in the contradiction that was retained. Then
we calculate the semantic similarity between them
and Altshuller’s generalized parameters, returning the
most similar one(s). Finally, the prototype returns the
inventive principles that should be used to solve the
contradiction.
AN APPLICATION OF SEMANTIC DISTANCE BETWEEN SHORT TEXTS TO INVENTIVE DESIGN
265
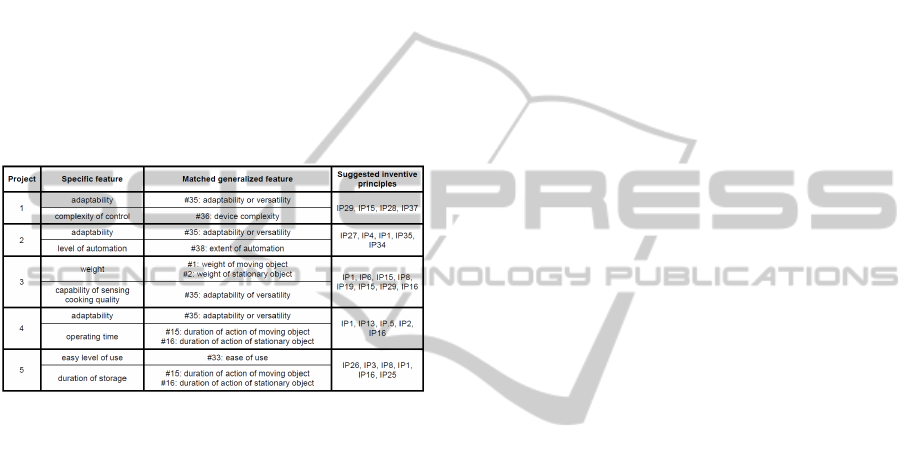
Some of the results of the experiments are shown
in Figure 2. We remark that there are two types of
projects. Sometimes, we obtain only one similar gen-
eralized feature for each specific feature (projects 1
and 2). But there are times, where two same values of
semantic similarity are obtained for the same specific
feature (projects 3, 4 and 5).
The results are encouraging if we compare with
the real solving process. For the first type of projects,
we can obtain the exact inventive principles obtained
manually by the students. For the second kind, we get
more inventive principles compared with the manual
work.
As stated above, we verify that our method can
facilitate the task of looking for inventive principles
efficiently and accurately.
Figure 2: The results of the experiments.
6 CONCLUSIONS
The gradual development of inventive design tech-
niques provokes that numerous knowledge sources
are available for experts to solve inventive problems
in different technical and non-technical fields. In real-
world problems, most of the times, the problems are
established in terms of parameters that are inherent
to the artefact that is being developed, and there is
a semantic gap to fill between those parameters and
the generalized ones. An abstraction effort needs to
be provided to choose the best generalized parame-
ter, and in this way, be able to use the contradiction
matrix.
In this paper, we present the inventive principles
ontology we have established as a support for our ap-
proach. According to this ontology, we propose to
measure the semantic distance between the parame-
ters intervening in the contradiction and the 39 gen-
eralized parameters, to help the user fill that semantic
gap and facilitate the process of using the contradic-
tion matrix.
In the future research, we need to improve our
method of semantic similarity calculation to adapt
to the semantic mapping among different knowledge
sources, such as inventive principles and inventive
standards.
REFERENCES
Agirre, E. and Rigau, G. (1996). Word sense disambigua-
tion using conceptual density. In Proceedings of the
16th conference on Computational linguistics - Vol-
ume 1, COLING ’96, pages 16–22, Stroudsburg, PA,
USA. Association for Computational Linguistics.
Altsthuller, G. (1984). Creativity as an Exact Science. Gor-
don and Breach Scientific Publishers, New York.
Altsthuller, G. (1999). TRIZ The innovation algorithm; sys-
tematic innovation and technical creativity. Technical
Innovation Center Inc., Worcester, MA.
Budanitsky, A. (1999). Lexical semantic relatedness and its
application in natural language processing. In Natural
Language Processing.
Cavallucci, D. and Eltzer, T. (9 November 2007). Parameter
network as a means for driving problem solving pro-
cess. International Journal of Computer Applications
in Technology, 30:125–136(12).
Fellbaum, C., editor (1998). WordNet: An Electronic Lexi-
cal Database. MIT Press, Cambridge, MA.
Jiang, J. and Conrath, D. (1997). Semantic similarity based
on corpus statistics and lexical taxonomy. In Proc.
of the Int’l. Conf. on Research in Computational Lin-
guistics, pages 19–33.
Lin, D. (1998). An information-theoretic definition of sim-
ilarity. In Proceedings of the Fifteenth International
Conference on Machine Learning, ICML ’98, pages
296–304, San Francisco, CA, USA. Morgan Kauf-
mann Publishers Inc.
Rada, R., Mili, H., Bicknell, E., and Blettner, M. (1989).
Development and application of a metric on semantic
nets. IEEE Transactions on Systems, Man and Cyber-
netics, 19(1):17–30.
Rahm, E. and Bernstein, P. (2001). A survey of approaches
to automatic schema matching. In The International
Journal on Very Large Data Bases (VLDB).
Resnik, P. (1995). Using information content to evaluate
semantic similarity in a taxonomy. In Proceedings of
the 14th international joint conference on Artificial in-
telligence - Volume 1, pages 448–453, San Francisco,
CA, USA. Morgan Kaufmann Publishers Inc.
Sussna, M. (1993). Word sense disambiguation for free-
text indexing using a massive semantic network. In
Proceedings of the second international conference on
Information and knowledge management, CIKM ’93,
pages 67–74, New York, NY, USA. ACM.
Tennant, G. (2003). Pocket TRIZ for Six Sigma. Mulbury
Consulting Limited, Bristol, England.
KEOD 2011 - International Conference on Knowledge Engineering and Ontology Development
266
