MEASURING TWITTER USER SIMILARITY
AS A FUNCTION OF STRENGTH OF TIES
John Conroy, Josephine Griffith and Colm O’Riordan
Information Technology, National University of Ireland, Galway, Ireland
Keywords: Twitter, Social media, Microblogging, Information retrieval, Social networks.
Abstract: Users of online social networks reside in social graphs, where any given user-pair may be connected or
unconnected. These connections may be formal or inferred social links; and may be binary or weighted. We
might expect that users who are connected by a social tie are more similar in what they write than
unconnected users, and that more strongly connected pairs of users are more similar again than less-strongly
connected users, but this has never been formally tested. This work describes a method for calculating the
similarity between twitter social entities based on what they have written, before examining the similarity
between twitter user-pairs as a function of how tightly connected they are. We show that the similarity
between pairs of twitter users is indeed positively correlated with the strength of the tie between them.
1 INTRODUCTION
Online social networks (OSNs) are defined by
connections between online social entities. Social
networks like facebook and twitter represent virtual
societies where human users can make friends,
chat, share media and generally interact in ways
which mimic real-life social interactions.
The aim of this research is to compare similarity
between user-pairs in a social network (twitter) as a
function of the strength of the social connection
between them. This research question requires (1)
that we find a measure of the strength of social
connectedness between a pair of users; and also (2) a
method of measuring similarity between a pair of
users.
We use the formal and inferred social graph data
of a twitter dataset to determine social connection
strength between users, and information retrieval
methods, applied to what users have written, to
acquire a measure of similarity between them.
We offer a broad definition of “social
connection” to be that quality which defines how
strong one’s acquaintanceship is with another
person. We assume a person who interacts
frequently with another person has a relatively
strong social connection with him. We further
assume, guided by evidence in other research
(Wilson, 2009), that users who interact with each
other in an OSN are more strongly socially coupled
than those who merely connect in a formal way.
This is the distinction between users who are
formally “friends” on facebook but never interact,
e.g. by posting on each others’ facebook Walls; and
those who do interact with each other. We make a
further assumption: that more frequent interaction
between users in an OSN implies greater social
connectedness between them. We simplify this
model of social connectedness by disregarding edge
direction between nodes in these formal and inferred
social graphs in our experiments. Thus, we suggest a
simple hierarchy of “social connectedness” whereby
users who are formally “friends” in the OSN are
more strongly socially linked than those who are
not; where users who interact with each other are
more strongly connected than those who are merely
formally “friends”; and where users who interact
with each other frequently are more strongly-linked
than those who interact less frequently. We explore
user similarity in the context of this hierarchy of
“social connectedness”.
We use information retrieval methods to
empirically measure the similarity between the tweet
contents of twitter users. Specifically, we convert the
corpus of what each user has written to tf-idf
weighted vectors, comparing these using cosine-
similarity. We then use this similarity measurement
to investigate differences between twitter users who
are linked and unlinked in the overt social graph,
and investigate user similarity between users who
262
Conroy J., Griffith J. and O’Riordan C..
MEASURING TWITTER USER SIMILARITY AS A FUNCTION OF STRENGTH OF TIES.
DOI: 10.5220/0003661902540262
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 254-262
ISBN: 978-989-8425-79-9
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

are linked or unlinked in the conversation/interaction
graph, to measure similarity as a function of the
strength of social connection.
The outline of the paper is as follows. In Section
2, we discuss related work on vector space analysis
of documents, social network analysis, and
interesting work which has been conducted on
twitter data. Section 3 introduces important concepts
for interpreting this paper, the data we used, details
on pre-processing of data and details on the methods
we used. Section 4 contains the results from our
experiments in analysing twitter user similarity as a
function of network connectedness, and our
interpretation of these results. Finally, we offer our
conclusions on this work and point towards possible
future research.
2 RELATED WORK
AND THEORY
In the vector space model, we consider a group of
documents which we wish to compare to each other,
or against a query term, to find close matches.
Documents are converted to high-dimension vectors
and compared in a common vector space
(Salton,1997). Commonly, we assign weights to
terms in the vocabulary set to adjust for relative
importance of certain terms. Prominent amongst
these is term frequency-inverse document frequency
(tf-idf) weighting, which weights term importance in
a document by that term's frequency in both the
document and the document set. A word which
appears in a given document, and infrequently in the
rest of the documents in a corpus, is more
descriptive of that document than another word
which appears frequently across all documents.
(Raghavan and Schutze, 2008). Thinking of
documents as vectors dates back to the Luhn and the
1950’s (Luhn, 1957), but it was the 1970’s before a
formal vector space model of representing and
comparing documents was proposed by Salton
(Salton, 1975).
Formal social network analysis dates back at
least as far as the Milgram experiments (Milgram,
1967) of the 1960s. While once the preserve of the
social sciences, the rich graph structure and
archivability of user interactions of web-based
communication platforms saw a surge of interest in
computational social graph analysis from the late
1990s.
Earlier analysis focused on data derived from
communication platforms such as Usenet and IRC
logs, and the increasingly ubiquitous email, which
usually had no formal graph structure. Often of more
interest to researchers in the field nowadays are
online social networks such as facebook and twitter,
where formal social ties are fundamental, and where
usage is defined in large part as a function of social
connectedness in a social graph.
Social entities can be considered to be connected
in different ways, at different levels of cohesion.
Early work in social network analysis reached
puzzling conclusions on the nature of social graphs,
such as short graph diameter (Milgram, 1967) and
the importance of weak links, for instance in
information diffusion between graph clusters
(Granovetter, 1973). Later work saw breakthroughs
in understanding the complex structure and
properties of social graphs, including their power-
law/ scale-free nature (Watts, 1998), the complex
growth dynamics associated with them, including
the phase shift from unconnectedness to the
formation of a giant connected component
(Barabasi, 1999), clustering and group dynamics
evident in such networks (Newman, 2003) and so
on. Liu and Slotine’s recent work (Liu, 2011) in
‘controllability’ of complex networks represents a
breakthrough in complex network theory,
specifically in identifying those nodes which dictate
dynamics and in finding to what extent it is viable to
‘control’ a given network’s dynamics, and is likely
to find applications in numerous scientific, economic
and other fields.
Huberman (2009) derived the conversation graph
(an example of an interaction graph) in a twitter
dataset, finding that this much sparser graph better
indicated community involvement and post-
frequency of individual users. Kumar et al. (2011)
used conversation graphs in Usenet groups, Yahoo!
Groups and twitter data to examine conversation
threads; how conversations form, to what depth they
persist through layers of users in the conversation
graph, and the group properties of these
conversation threads. Romero (2011) utilised graphs
generated from conversations around twitter
hashtags to investigate viral properties of topics
discussed, and to test the sociological "complex
congtagion" hypothesis, which postulates that
continual exposure to ideas correlates strongly with
a person's adoption of new beliefs and ideas. Ritter
et al. (2010) used a dataset of 1.3 million twitter
posts to develop an innovative unsupervised
conversation model, the aim of which is to
determine the intent of a conversation action (e.g.
whether a conversation action is best classified as a
query, a reaction, an answer, a reference broadcast
etc.). Backstrom's analysis (2008) including using
MEASURING TWITTER USER SIMILARITY AS A FUNCTION OF STRENGTH OF TIES
263

conversations in social network data (a Yahoo!
groups dataset) to examine the depth and meaning of
social engagement between users, formalising levels
of user interaction and the roles and importance of
heavily involved nodes in such interaction graphs.
Other innovative applications of twitter data
include predicting box-office earnings for
Hollywood movies (Asur, 2010) and sentiment
analysis of TV viewers reception of Superbowl
commercials using machine learning (Conroy, 2010).
3 DATASET, ESSENTIAL
CONCEPTS AND METHODS
3.1 Two Social Graphs
Social entities (twitter users) reside in numerous
social graphs concurrently. We focus on two such
graphs. Twitter users may subscribe to other users’
posts by clicking a “follow” button on that user’s
profile page. This mechanism is the primary social
facility which defines the twitter community. We
hereafter call this graph the formal social graph. It
is analogous to the formal graph generated by the
“friend” construct on facebook or the “subscribe”
construct on YouTube.
As well as the formal graph generated by
“friend” relationships, we derive the graph generated
by users who engage in direct conversation with
each other. Twitter users can direct messages to
other users by including an “@SomeOtherUser”
token in their posts, if they want to direct a message
for the attention of “SomeOtherUser”. We extract
this graph from the posts of twitter users. We
hereafter refer to this graph as the conversation
graph. It may also be thought of as an “interaction
graph”, as it is a graph derived from interactions
between users. This graph is analogous to a graph
derived from facebook users posting on other users’
walls; or from YouTube users commenting on other
users’ videos.
3.2 Two Types of User Documents:
Text Documents and Hashtag
Documents
Twitter users post short updates of 140 characters or
less, referred to as tweets or posts. From our dataset
of tweets, we create two documents for each user,
one comprised of everything they have written
(which is preprocessed before analysis), and one
comprised merely of the hashtags used by the user.
The first user document we create contains the
full concatenated text of all of their posts, which is
then preprocessed in various ways, including
removing stop words, removing punctuation etc. We
hereafter call this document the text document for
that user.
The second document we generate for each user
contains only the hashtags contained in their posts.
Twitter posts may contain hashtags
(“#someSubject”), which are analogous to blog post
tags, and are used to denote the subject of a
particular post. This second document contains only
the hashtags posted by that user. We call this
document the hashtag document of a user.
The data used in our analysis is de Chowdury’s
dataset (de Chowdury, 2010) of twitter posts and
formal follower/following relationships between users.
3.3 Comparing Documents:
Tf-idf Weighting and Vector Space
As already mentioned, two documents are generated
for each user: the text document and the hashtag
document. We convert all documents to tf- idf
weighted vectors, then compare pairs of documents
in vector space to find a measure of similarity
between them.
3.4 Dataset and Preprocessing
De Chowdury’s dataset (de Chowdury, 2010) is
comprised of ~ 400k twitter users, over 800k formal
edges between users, and 10,309,384 posts by those
users. To attain a sample set of users suitable for
document analysis, we discarded those users which
posted fewer than four times, leaving approximately
110k users. This set of 110k users and their posts
comprises our dataset.
As discussed, for each user, we created two
documents: one which contained all of their
concatenated posts in the dataset (their text
document), and one which contained all the hashtags
from those posts (their hashtag document). We
preprocessed users text documents by removing stop
words, converting to lower case, and removing
hyperlinks and retweets.
3.5 Experiments
Users in a social graph may be connected in
different ways, with different strengths of ties
between them. The most obvious form of linkage in
a graph of twitter users is that described by
follower/following relationships: the formal social
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
264

graph. Subscribing to another twitter user
(“following” that user) suggests some commonality
or shared interest. We wish to empirically measure
this similarity, and find some magnitude of
similarity between linked users.
Specifically, our work focuses on measuring
similarity between user pairs as a function of the
strength of social ties between those users. We
investigate:
1. similarity between users who are linked in the
formal social graph against those who are not,
2. similarity between users who engaged in
conversation with each other against those who did not,
3. similarity between those who are linked in
the formal graph against those who are linked in the
conversation graph,
4. similarity between users in the conversation
graph as a function of the number of conversation
actions between them.
4 RESULTS
4.1 Similarity in the Formal Graph
To find similarity between users in the formal graph,
we took 19886 pairs of users who were linked to
each other via follower/following relationships, and
measured the cosine-similarity between the
documents of each of these pairs of users. We
compared this with the mean cosine similarity
between a random sample of over 63k non-linked
user pairs in the formal graph. Table 1 shows the
results.
Table 1: (P(H0): x
̅
{linked scores} ≤ x
̅
{unlinked scores}
<.001 (t stat.=-81)
1
).
Formal graph:
text documents
Mean
similarity
Std
dev
Median IQR (inter
quartile range)
Linked User
Pairs
(
19886
)
0.0352 0.064 0.01558 0.00563 -0.03756
Random
unlinked user
Pairs (63412)
0.0121 0.018 0.00729 0.00230 - 0.0162
----------------------------------------------------------------------------------------------------------------------
1
Statistical significance in our data.
Any t-scores present in this document refer to the following
expression:
H
0
: {linked scores} ≤ {unlinked scores},
H
1
: {linked scores} > {unlinked scores}
P(H
0
) refers to the hypotheses stated above in each case, and
refers to the
probability that a different random sample of
unlinked user pairs would have a greater-or-equal-to mean
similarity score as the sample of linked user pairs. Thus, a very
low p value quates to a high degree of significance between sets
of scores.
The mean and median similarities of linked user-
pairs in Table 1 is well above that for unlinked pairs,
indicating that the documents of users who
are linked in the formal graph are more similar
than t h o s e o f unlinked users, taking the full text
of everything they have written (after generic
preprocessing) as the criteria. For the first time, we
can measure not only whether linked users are more
similar than unlinked users in a social graph, but can
measure the difference. The difference between
linked and unlinked user pairs is more clearly
illustrated in the box plot in Figure 1.
Figure 1.
Figure 2: Distribution of similarity scores between linked
and unlinked users in the formal social graph, using text
documents.
As well as text documents for each user
containing everything they have written, we also
have hashtag documents for each user containing
only the hashtags they used in these posts. We
perform the same analysis on these users’ hashtag
documents as we performed on their text documents,
to see if the same trend holds in the formal graph.
Again we see (Table 2) that the documents of
linked user-pairs are far more similar than are
MEASURING TWITTER USER SIMILARITY AS A FUNCTION OF STRENGTH OF TIES
265

unlinked users. We cannot directly compare scores
from the hashtag- document analysis with text-
document scores, as the vectors describing each are
of different dimensions, with different tf-idf
weightings. However the relative difference of
linked users vs. unlinked users seems far stronger
when using hashtags. This indicates that the
hashtags which twitter users use are better at
showing up differences between users than text. By
definition, hashtags are more indicative of the topic
of a post than any given word. The relative noise
associated with hashtags is far less, when using them
as descriptors of a user, than the raw text posted by
that user.
Table 2: P(H0) x
̅
{linked scores} ≤ x
̅
{unlinked scores}
<.001.
Formal graph:
Hashtag documents
Mean
similarity
Std
dev.
Median IQR (inter
quartile range)
Linked User
Pairs (19886)
0.0231 0.1002 0 0-0
Random
unlinked user
Pairs (63412)
0.0034 0.0312 0 0-0
Using hashtags in comparative analysis of users
does have a drawback, however: sparseness. This
problem is hinted at in Table 2 above, where we see
median and quartile intervals of zero. Hashtag usage
is relatively rare, and very often (more than 75% of
the time), when we compare two hashtag documents,
we find that there is no similarity at all. Just like the
distribution for similarities between users when
using text documents (Figure 1), the distributions of
similarity scores between linked users and unlinked
users is heavily skewed-right, with a preponderance
of very low scores. This tendency is amplified when
comparing hashtag documents.
4.2 Similarity of Users
in the Conversation Graph
The above section dealt with similarity between
linked and non-linked users in the formal social
graph created by follower/following relationships.
Another form of social linkage lies in the graph
created by users interacting meaningfully with each
other. The most prominent way in which twitter
users interact with each other is via directing
messages to each other with the “@someUser”
syntax. These tokens represent acts of conversation,
and we can derive the conversation graph from these
messages.
It may be assumed that such implied or inferred
“interaction” graphs are more meaningful in terms
of social connectedness, and reflect a more genuine
social cohesion than the formal social “friend”
links. Intuitively this is so, and researchers Wilson
(2009) have found evidence supporting this view. If
so, we might expect a higher level of similarity
between users linked in this graph, than against
random user pairs. We analyse similarity in the
conversation graph in the same way as we did
the formal graph previously, both for users’ text
documents and hashtag documents.
Table 3: (P(H0): x
̅
{linked scores} ≤ x
̅
{unlinked scores}
<.001.
Conversation graph
similarity:
text documents
Mean
sim.
Std dev. Median IQR
Linked User Pairs
(16958)
0.0696 0.100 0.048 0.023-0.075
Random unlinked
user Pairs (59999)
0.0112 0.018 0.006 0.002-0.014
Table 4: (P(H0): x
̅
{linked scores} ≤ x
̅
{unlinked scores}
<.001.
Conversation graph
similarity: Hashtag
documents
Mean
sim
Std dev. Median IQR
Linked User Pairs
(19958)
0.0756 0.166 0.0 0.0-0.06
Random unlinked
user Pairs (60000)
0.0019 0.014 0.0 0.0-0.0
Figure 3: Similarity of linked user pairs vs. unlinked
user pairs in the conversation graph, using users’ text
documents.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
266

As we can see in Table 3 and Table 4, similarity
between user pairs who engaged conversationally
was far greater than the mean similarity of random
user pairs who did not interact with each other,
whether using text documents or hashtag documents
to compare them. Although the difference is
relatively much greater when considering hashtag
documents, the sparseness of this data must be
considered once again: frequently, linked and
unlinked user pairs score zero for similarity in their
hashtag document vectors, albeit zero-scores are
more common with unlinked users.
4.3 Similarity in Linked Users as a
Function of Connectedness:
Formal vs Conversation Graph
The pattern is becoming clear: socially linked users
are more similar in terms of what they have written
than unlinked users, whether we consider the full
text of their posts or merely the hashtags they used.
This is exactly what we would expect: people who
are connected socially are more likely to have more
in common than random strangers, and the contents
of their posts should reflect this. But an interesting
question now arises: are users who are linked in the
conversation graph more or less similar than users
who are linked only in the formal graph, suggesting
evidence of greater social cohesion in the
conversation graph? And, as the conversation graph
is a weighted one, with one or multiple conversation
actions between users, is there any correlation
between similarity and the number of conversations
users had?
The text document similarities for the formal
graph and the conversation graph exist in the same
vector space: they share the same dimension space
(defined by the vocabulary) and associated tf-idf
parameters. We can thus compare them directly. We
find that similarity between users who engaged in
conversation (mean=0.0696 when using text
documents, Table 3) is significantly greater than the
similarity between users who are linked in the
formal graph (mean=0.0352 for text documents,
Table 1). This suggests some stronger measure of
social cohesion in the conversation graph. Figure 4,
below, illustrates better this marked difference.
Figure 4: Similarity of linked user pairs in the formal
graph against linked user pairs in the conversation graph.
4.4 Similarity between Users in the
Conversation Graph as a Function
of Number of Conversation Actions
A question naturally arises. Given that we can now
see marked differences in similarity of users based
on whether they are strongly socially coupled
(conversation graph) or more loosely socially
connected (formal graph), how far can we take this
analysis in terms of connectedness? Does similarity
between user pairs increase generally as the strength
of the social tie between them grows?
We first need some formal measurement of
strength of ties between users. The formal graph is
not useful in this regard: edges in this graph are
unweighted, and tell us nothing about the relative
strength of a social tie between two users. The
conversation graph, however, is different. This graph
is naturally weighted, because a given user may
converse with another user one or many times. We
may thus be permitted to make the following
assumption: that more conversation actions between
two users implies a stronger social bond between
those users. Working from this assumption, we can
analyse user similarity as a function of connection
strength in this graph, and discover whether higher
levels of connectedness correlate with higher levels
of user similarity. We can also attempt to form an
expression to describe this relationship.
The goal, then, is to uncover any correlation
between the number of conversation actions between
users and the similarity between them. Given the
sparseness problem associated with similarity scores
between hashtag document vectors, we focus on
users’ text documents.
We can examine the similarity scores between
user pairs who conversed once, comparing these
MEASURING TWITTER USER SIMILARITY AS A FUNCTION OF STRENGTH OF TIES
267

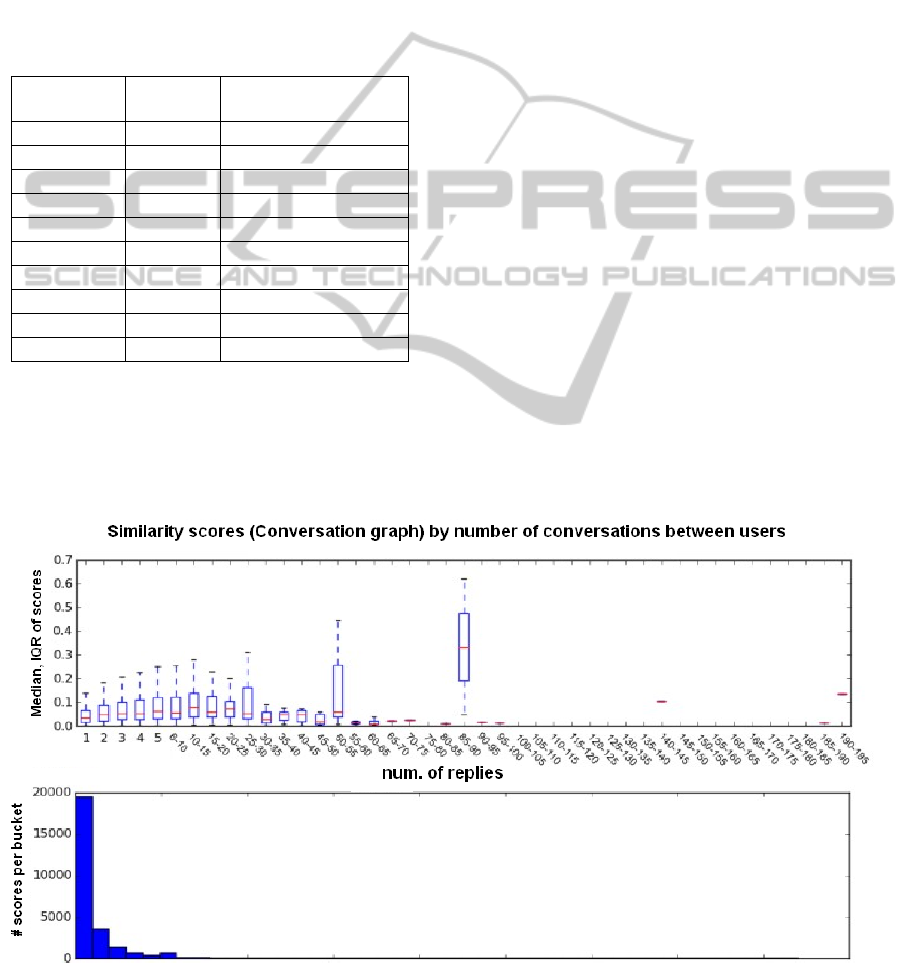
with similarity scores of users who conversed twice,
and so on. The frequency distribution of the
conversation graph is heavily skewed towards the
lower end, such that user pairs who conversed once
are more numerous than those who conversed twice,
and these in turn are more numerous than pairs who
conversed three times, and so on. Once we begin to
look at users who conversed more than five times,
data becomes sparse. We thus use increasing bin
sizes for this analysis.
Table 5: Mean user similarity by the number of
conversation actions between them.
# Conversations # Edges
Mean score
(
text document s
i
m
i
lar
i
t
y)
1 19469 0.0596
2 3497 0.07984
3 1350 0.08947
4 646 0.10263
5 354 0.10389
6-10 627 0.10405
11-15 142 0.13024
16-50 161 0.10129
51-100 20 0.08447
>100 3 0.08355
As can be seen in Table 5, the correlation is clear for
lower numbers of conversation actions: the more
two users conversed with each other, the more
similar they are in what they have written. This
correlation begins to break down for higher levels of
conversations (those with 16-50 conversation actions
are less similar than those who with 11-15 such
actions, and so on). Data is beginning to become
sparse at this point for these user pairs. The
sparseness of data for those who conversed more
than 15 times perhaps explains this discrepancy, or
perhaps automated spam: intuitively, we can offer
no deeper explanation for this discrepancy. What is
clear, however, is that there is a clear correlation
between the number of conversations which two
users had, and the similarity between them, at least
up to this tipping point. We map the medians and
IQRs for these data points in Figure 5, this time in
slightly more detail in terms of bin sizes. We also
show the frequency distribution for the number of
conversations between users.
The correlation between the number of
conversations between users and the similarity of
their documents is noticeably well-behaved and
predictable, for low numbers of conversations at
least (where we have significant data). It seems,
overall, that aggregating users’ posts into
documents, and comparing these in vector space,
holds promise as a tool in social network analysis, in
areas like community detection and recommendation
engines, where such methods may be applied to test
and compare the efficacy of various graph-based
algorithms.
Figure 5: Similarity scores in the conversation graph per edge weight.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
268

5 CONCLUSIONS
We offer a method of measuring similarity between
twitter users based on what they have written,
fitting their aggregated posts to tf-idf weighted
vectors and comparing them in vector space.
We use this data to measure similarity
between users as a function of the connectedness
between them. We find that users who are
connected in either the formal graph or the graph
derived from conversations are more similar than
unlinked users. We furthermore find that users who
conversed with each other are more similar than
users who are linked in the formal
“follower/following” social graph. We consider
connections in the sparser conversation graph to be
more meaningful and to represent stronger social
ties than formal links, and these results all indicate
a positive correlation between social connectedness
in a social graph, and similarity in terms of what
one posts.
Taking this analysis further, we use the
natural weighting of the conversation graph to
analyse user similarity as a function of how
strongly connected they are. The conversation
graph is weighted, in that users in it converse with
each other one or many times. We find that the
similarity of twitter users correlates well with the
number of conversation actions between them, up
to a tipping point of around 15 conversations,
whereafter the similarity between users begins to
decline (though the sparseness of data for users who
conversed more than 15 times may account for this
abberation).
The document-analysis approach we used to
investigate user similarity, borrowed from the field
of information retrieval, holds promise as a method
of comparing the relative efficacy of graph-based
algorithms in common social network analysis
fields, such as community detection and
recommendation systems.
REFERENCES
Asur S., Huberman B. A., 2010, Predicting the future
with social media, IEEE/WIC/ACM International
Conference on Web Intelligence and Intelligent Agent
Technology
Backstrom, L., Kumar, R., Marlow, C., Novak, J., 2008.
Preferential behaviour in online groups. In
Proceedings of the international conference on Web
search and web data mining (WSDM) 2008
Barabasi, A. L., Albert, R., 1999, Emergence of scaling in
random networks, Science 286, pp 509-512
Bush, V., 1939. Mechanization and the record, Vannevar
Bush Papers, Library of Congress [U.S.A.] Box 138,
speech article book file
Bush, V., Wang, J., 1945, Atlantic Monthly 176 pp101-
108
Conroy, J., Griffith, J. 2010 Machine learning techniques
for sentiment analysis of Super Bowl commercials,
The 21st National Conference on Artificial
Intelligence and Cognitive Science (AICS), NUI
Galway, Ireland
Cummins, R., O'Riordan, C., 2007 An axiomatic
comparison of learned term-weighting schemes in
information retrieval: clarifications and extensions,
Artificial Intelligence Review 28
de Chowdury, M., Lin, Y. R., Sundaram, H., Candan, K.
S., Lexing, X., Kelliher, A.. 2010. How does the data
sampling strategy impact the discovery of information
diffusion in social media. Fourth International AAAI
Conference on Weblogs and Social Media.
Dong, A., Zhang, R., Kolari, P., Bai, J., Diaz, F., Chang,
Y., Time is of the essence: improving recency ranking
using Twitter data. In Proceedings of WWW '10
Proceedings of the 19th international conference on
World wide web ACM New York
Granovetter, J. M. 1973. The strength of weak ties.
American Journal of Sociology 78(6)
Huberman B. A., Romero, D. M. Wu, F., 2009 Social
networks that matter: twitter under the microscope,
First Monday 14
Kumar, R., Mahdin, M., McGlohan, 2011, Dynamics of
Conversations, ACM Special Interest Group on
Knowledge Discovery and Data Mining (KDD10).
Washington DC
Liu, Y-Y., Slotine, J-J., Barabasi, A. L. 2011,
Controllability of complex networks, Nature, Volume
473 Number 7346
Livnel, A., Simmons, M. P., Adarl, E., Adamic, L.A.,
2011, The Party is Over Here: Structure and Content
in the 2010 Election, ICWSM 2011
Luhn, H. P. 1957. A statistical approach to the
mechanized encoding and searching of literary
information, IBM Journal of Research and
Development 1:4, 309-317
Magnani, M., Montesi, D., Nunziante, G., Rossi, L.,
2011, Conversation retrieval from Twitter, Lecture
Notes in Computer Science Volume 6611/2011, 780-
783
Milgram, S., 1967. The small world problem. Psychology
Today 2:60-67
Newman M. E. J, 2003, The structure and function of
complex networks. SIAM Review 45, pp 167-256
Raghavan, P., Schütze, H. 2008. Introduction to
Information Retrieval, Cambridge University Press
pp 117-120, 121-124
Ritter, A. Cherry, C., Dolan, B., 2010, Unsupervised
modeling of twitter conversations, HLT '10: Human
Language Technologies: The 2010 Annual
Conference of the North American Chapter of the
Association for Computational Linguistics
MEASURING TWITTER USER SIMILARITY AS A FUNCTION OF STRENGTH OF TIES
269

Romero, D. M., Meeder, B., Kleinberg, J., 2011.
Differences in the mechanics of information diffusion
across topics: idioms, political hashtags and complex
contagion on twitter. In Proceedings of the 20th Intl.
Conference on World Wide Web WWW 2011
Salton, G., Wong, A., Yang, C. S. 1997 A vector space
model for automatic indexing. Readings in
information retrieval. Morgan Kaufman publishers.
Salton, G., 1991. Developments in automatic text
retrieval. Science 253 pp 974-980
Singhal, A., 2001, Modern information retrieval: a brief
overview, Bulletin of the IEEE computer society
technical committee on data engineering
Soucy, P. 2005. Beyond TFIDF weighting for text
categorization in the vector space model. In
Proceedings of the 19th International Joint
Conference on Artificial Intelligence (IJACAI 2005)
Watts, D. J., Strogatz, S.H., 1998, Collective dynamics
of‘small-world’ networks. Nature Volume 393, pp
330-442
Wilson, C., Boe, B., Sala, A., Puttaswamy, P. N., Zhao,
B., 2009, User interactions in social networks and
their implications, ACM EuroSys
Zheng, Z. 2010. Time is of the essence: improving
recency ranking using Twitter data. In Proceedings
of WWW '10 Proceedings of the 19th international
conference on World wide web ACM New York
Zipf, G. K. 1932. Selected studies of the principle of
relative frequency in language. Harvard University
Press.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
270