
FEATURE DISCRETIZATION AND SELECTION
IN MICROARRAY DATA
Artur Ferreira
1,3
and M´ario Figueiredo
2,3
1
Instituto Superior de Engenharia de Lisboa, Lisboa, Portugal
2
Instituto Superior T´ecnico, Lisboa, Portugal
3
Instituto de Telecomunicac¸˜oes, Lisboa, Portugal
Keywords:
Feature selection, Feature discretization, Microarray data, Tumor detection, Cancer detection.
Abstract:
Tumor and cancer detection from microarray data are important bioinformatics problems. These problems are
quite challenging for machine learning methods, since microarray datasets typically have a very large num-
ber of features and small number of instances. Learning algorithms are thus confronted with the curse of
dimensionality, and need to address it in order to be effective. This paper proposes unsupervised feature dis-
cretization and selection methods suited for microarray data. The experimental results reported, conducted on
public domain microarray datasets, show that the proposed discretization and selection techniques yield com-
petitive and promising results with the best previous approaches. Moreover, the proposed methods efficiently
handle multi-class microarray data.
1 INTRODUCTION
Datasets with large numbers of features and (rela-
tively) smaller numbers of instances are challenging
for machine learning methods. In fact, it is often the
case that many features are irrelevant or redundant for
the classification task at hand (Guyon et al., 2006), a
situation that may be specially harmful in the pres-
ence of relatively small training sets, where these ir-
relevancies/redundancies are harder to detect.
To deal with such datasets, feature selection (FS)
and feature discretization (FD) methods have been
proposed to obtain representations of the dataset that
are more adequate for learning. A byproduct of FD
and FS is a reduction of the memory requirements to
represent the data as well as an improvement on the
classification accuracy. FD and FS are topics with a
long research history, thus with a vast literature; re-
garding FD, see (Dougherty et al., 1995; Witten and
Frank, 2005) for comprehensive reviews of unsuper-
vised and supervised methods; regarding FS, see for
instance (Guyon et al., 2006; Escolano et al., 2009).
1.1 Filter Methods for Microarray Data
In the past decade, there has been a great interest
on automated cancer detection from microarray data
(Guyon et al., 2002; Meyer et al., 2008; Statnikov et
al., 2005). The nature of microarray (many features,
small samples) makes it an almost ideal application
area for FD and FS techniques.
FD, FS, and a wide variety of classifiers have been
applied to gene expression data in order to obtain ac-
curate predictions of cancer and other diseases. The
use of FS techniques on gene expression data is often
called gene selection (GS); for a review of FS tech-
niques in bioinformatics, see (Saeys et al., 2007) and
the many references therein.
For learning on microarray data, there are several
filter approaches. In (Statnikov et al., 2005) multi-
category support vector machines (MC-SVM) are
compared against other techniques, such as k-nearest
neighbors (KNN), multilayer perceptrons (MLP), and
probabilistic neural networks (PNN). The use of FS
significantly improves the classification accuracy of
the MC-SVM and the other learning algorithms. A
FS filter for microarray data, proposed in (Meyer
et al., 2008), uses an information-theoretic criterion
named double input symmetrical relevance (DISR),
which measures variable complementarity. The ex-
perimental results show that the DISR criterion is
competitive with existing FS filters. Regarding clas-
sification methods, SVM classifiers attain the best re-
sults (Bolon-Canedo et al., 2011; Meyer et al., 2008;
Statnikov et al., 2005). Despite the large number of
wrapper approaches for this problem, in this short pa-
465
Ferreira A. and Figueiredo M..
FEATURE DISCRETIZATION AND SELECTION IN MICROARRAY DATA.
DOI: 10.5220/0003662004570461
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 457-461
ISBN: 978-989-8425-79-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

per we consider solely filter methods due to their effi-
ciency on high-dimensional datasets.
1.2 Our Contribution
In this paper, we propose unsupervised methods for
FD and FS on medium and high-dimensional microar-
ray datasets. These methods address the main draw-
back of previous approaches, that is, their difficulty
to accurately handle multi-class microarray datasets.
The FS method follows a filter approach (Guyon
and Elisseeff, 2003), with a relevance and rele-
vance/similarity analysis, being computationally effi-
cient in both terms of time and space.
The remaining text is organized as follows. Sec-
tion 2 briefly reviews unsupervised FD and FS tech-
niques and their application on microarray data. Sec-
tion 3 presents the proposed methods for FD and FS,
along with our relevance/similarity analysis. Section
4 reports the experimental evaluation of our methods
in comparison with other techniques. Finally, section
5 ends the paper with some concluding remarks and
directions for future work.
2 LEARNING IN MICROARRAY
DATA
This section reviews some FD and FS techniques that
have been applied to microarray datasets.
2.1 Feature Discretization
FD has been used to reduce the amount of memory as
well as to improve classification accuracy (Dougherty
et al., 1995; Witten and Frank, 2005). In the context
of unsupervised scalar FD, two techniques are com-
monly used:
. equal-interval binning (EIB), i.e., uniform quan-
tization with a given number of bits for each fea-
ture;
. equal-frequency binning (EFB), i.e., non-uniform
quantization yielding intervals such that for each
feature the number of occurrences in each interval
is the same, yielding a discretized variable with
uniform distribution, thus maximum entropy; for
this reason, this technique is also named maximum
entropy quantization.
The EIB method divides the range of values into
bins of equal width. It is simple and easy to imple-
ment, but it is very sensitive to outliers, and thus may
lead to inadequate discrete representations. The EFB
method is less sensitive to the presence of outliers.
The quantization intervals have smaller width in re-
gions where there are more occurrences of the values
of each feature. It has been found by different authors
that FD methods tend to perform well in conjunction
with several classifiers (Dougherty et al., 1995; Wit-
ten and Frank, 2005). In (Meyer et al., 2008), FD is
applied with both EIB and EFB to standard microar-
ray data using SVM classifiers.
2.2 Feature Selection
Many supervised and unsupervised FS techniques
have been applied to microarray data; see (Saeys
et al., 2007) and the many references therein. We
briefly outline some of the most common techniques.
Since microarray datasets are typically labeled, the
supervised FS techniques has been preferred over the
unsupervised counterparts.
Many of these supervised FS techniques are
information-theoretic. For instance, the min-
imum redundancy maximum relevancy (mRMR)
method (Peng et al., 2005) adopts a filter approach,
being fast and applicable with any classifier. The
key idea in mRMR is to compute both the redun-
dancy among features and the relevance of each fea-
ture. The redundancy is assessed by the mutual infor-
mation (MI) between pairs of features, whereas rel-
evance is measured by the MI between features and
class label.
The (supervised) monotone dependence (MD) cri-
terion estimates the MI between features and class la-
bels (relevance analysis) and among features (redun-
dancy analysis) (Bolon-Canedo et al., 2011); the orig-
inal feature space is considered and the MD criterion
is applied for FS, whereas on their previous work the
same authors had considered FD techniques.
3 PROPOSED UNSUPERVISED
METHODS
3.1 Feature Discretization
For unsupervised scalar quantization of each feature,
we propose to use our method named unsupervised
FD (UFD), which is based on the well-known Linde-
Buzo-Gray (LBG) algorithm. The LBG algorithm is
applied individually to each feature and stopped when
the MSE distortion falls below a threshold ∆ or when
the maximum number of bits q per feature is reached.
Thus, a pair of input parameters (∆, q) is necessary;
we recommend to set ∆ equal to 5% of the range
of each feature and q ∈ {4,...,10}. For more de-
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
466

tails on our UFD algorithm, please see (Ferreira and
Figueiredo, 2011).
3.2 Filter Feature Selection
We propose two unsupervised filter FS meth-
ods for discrete features. The first approach is
termed relevance-only unsupervised feature selection
(RUFS), performing the following steps:
• compute the relevance @rel for each one of the p
features;
• sort features by their decreasing relevance;
• keep the first m (≤ p) features.
The number of features to keep m is obtained
based on a cumulativerelevance criterion given as fol-
lows; let {r
i
, i = 1, ...., p} be the relevance values for a
set of features and {r
(i)
, i = 1, ...., p} the same values
after sorting in descending order. We propose choos-
ing m as the lowest value that satisfies
m
∑
i=1
r
(i)
/
p
∑
i=1
r
(i)
≥ L, (1)
where L is some threshold (in the interval [0.7,0.9],
for instance). A simple alternative version of the
RUFS algorithm uses a pre-defined number of fea-
tures m (≤ p), rather than using the threshold L.
The relevance criterion @rel for feature X
i
is
given by
r
i
= var(X
i
)/b
i
, (2)
where b
i
≤ q is the number of bits allocated to feature
X
i
in the FD step, and var(X
i
) is the sample variance
of the original (non-discretized) feature. The key idea
of this criterion is: features with higher variance are
more informative than features with lower variance;
for a given feature variance, features quantized with
a smaller number of bits are preferable because we
can express all that variance (information) in a small
number of bits, for the same target distortion ∆.
Our second approach to FS is named rele-
vance/similarity unsupervised FS (RSUFS). As com-
pared to RUFS, it incorporates redundancy analysis
and removesthe most similar features among the most
relevant. After executing the same first two actions as
in RUFS, the RSUFS algorithm performs:
• keep the first feature;
• compute the similarity @sim between pairs of
consecutive features, say X
i
and X
i+1
, for i ∈
{1,..., p− 1};
• if the pairwise similarity @sim is above η, delete
feature X
i+1
and keep feature X
i
.
The similarity is computed between pairs of con-
secutive features sorted in decreasing relevance. The
RSUFS algorithm returns up to m features; if the sim-
ilarity analysis eliminates many features (depending
on the value of η), the final selected subset may con-
tain m ≪ p features. We propose to compute the simi-
larity between two features, X
i
and X
j
, by the absolute
value of the cosine of the angle between them,
|cos(θ
X
i
X
j
)| =
hX
i
,X
j
i
kX
i
k
X
j
, (3)
where h·,·i is the inner product and k·k is the ℓ
2
norm;
we have 0 ≤ |cos(θ
X
i
X
j
)| ≤ 1, with 0 holding for or-
thogonal features and 1 for linearly dependent fea-
tures. The choice of η in the interval [0.5,0.8] is ade-
quate.
3.2.1 Analysis and Extensions
The running time of RUFS and RSUFS is log-linear
with the number of features; RSUFS only evaluates
the similarities between consecutive features, com-
puting up to p − 1 similarities. This is an important
issue when dealing with microarray datasets, which
are medium to high-dimensional datasets.
Both RUFS and RSUFS algorithms can be mod-
ified to perform supervised FS: the @rel and @sim
functions must then make use of the class labels.
4 EXPERIMENTAL EVALUATION
The experimental evaluation is carried out on pub-
lic domain microarray gene expression datasets
1
. We
use linear SVM classifiers, provided by the PRTools
2
toolbox. All of these datasets, except one, correspond
to multi-class problems, being typical examples of the
“large p, small n” scenario. Table 1 shows the aver-
age accuracy for ten runs with random train/test set
partitions, for our RUFS algorithm on discrete fea-
tures obtained by UFD, using linear SVM classifiers.
We compare our results with those of Meyer et
al (Meyer et al., 2008), that uses FD by both EIB and
EFB methods; it also uses SVM and 3-nearest neigh-
bor (3-NN) classifiers. As compared to Meyer et al.
results, our proposed approach attains better results
on all of these datasets. Thus, the UFD discretization
is preferable to its EIB and EFB counterparts. For the
choice of L, we use 0.8 for the smaller dimensional
datasets and 0.7 for the higher-dimensional.
1
http://www.gems-system.org/
2
http://www.prtools.org/prtools.html
FEATURE DISCRETIZATION AND SELECTION IN MICROARRAY DATA
467
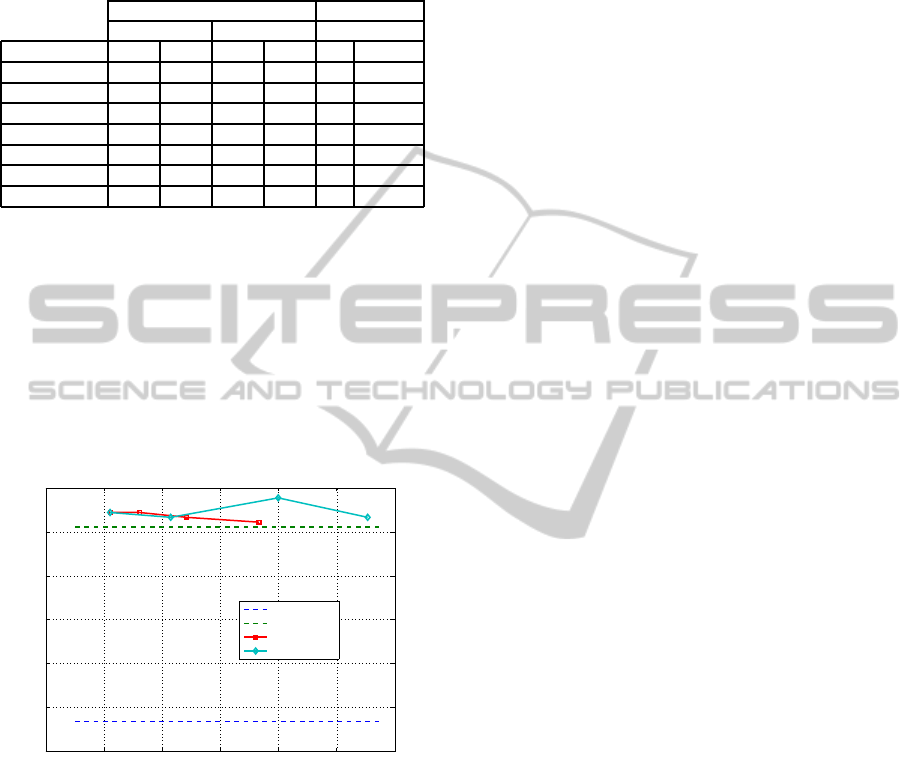
Table 1: Average accuracy for linear SVM and 3-NN clas-
sifiers for RUFS on discrete features obtained by UFD
(∆ = 0.05range(X
i
),q = 8). L is the cumulative relevance
threshold as in (1). The best accuracy is shown in bold, and
the symbol * signals multi-class problems.
(Meyer et al., 2008) Our Approach
EIB EFB UFD + RUFS
Dataset SVM 3-NN SVM 3-NN L SVM
SRBCT* 83.13 90.36 79.52 84.34 0.8 100.00
Leukemia1* 91.67 97.22 88.89 90.28 0.8 98.41
DLBCL 90.91 87.01 94.81 93.51 0.7 95.67
9 Tumors* 10.0 16.67 15.0 23.33 0.7 84.89
Brain Tumor1* 65.0 65.0 65.0 66.67 0.7 96.67
11-Tumors* 60.32 50.57 53.45 55.17 0.7 94.55
14-Tumors* 19.48 16.56 22.4 29.87 0.7 76.2
Figure 1 plots the accuracy (average over ten runs
with different random train/test partitions) for the
RUFS and RSUFS algorithms on UFD-discretized
features, as functions of the average number of fea-
tures m (computed by assigning values in the inter-
val [0.6,0.9] to the L and η parameters, respectively).
The horizontal dashed lines represent the average ac-
curacy on the original features, without and with dis-
cretization (blue and green lines, respectively). The
0 1000 2000 3000 4000 5000 6000
72
74
76
78
80
82
84
# Features (m)
[%]
Accuracy on the 9−tumors Dataset
Original
UFD
UFD + RUF
UFD + RSUF
Figure 1: Average accuracy of the linear SVM classifier
(ten runs, with different random train/test partitions) for the
RUFS and RSUFS algorithms on features discretized by
UFD and on the original features.
use of UFD shows improvement (about 9 %) as com-
pared to the use of the original features; the use of
RUFS and RSUFS further improves these results, us-
ing small subsets of features.
5 CONCLUSIONS
In this paper, we have proposed unsupervised meth-
ods for feature discretization and feature selection,
suited for microarray gene expression datasets. The
proposed methods follow a filter approach with rel-
evance and relevance/similarity analysis, being com-
putationally efficient in terms of both time and space.
Moreover, these methods are equally applicable to bi-
nary and multi-class problems, in contrast with many
previous approaches, which perform poorly on multi-
class problems. Our experimental results, on public-
domain datasets, show the competitiveness of our
techniques when compared with previous discretiza-
tion approaches. As future work, we plan to devise
supervised versions of the proposed methods for dis-
cretization and selection.
REFERENCES
Bolon-Canedo, V., Seth, S., Sanchez-Marono, N., Alonso-
Betanzos, A., and Principe, J. (2011). Statistical de-
pendence measure for feature selection in microar-
ray datasets. In 19th Europ. Symp. on Art. Neural
Networks-ESANN2011, pages 23–28, Belgium.
Dougherty, J., Kohavi, R., and Sahami, M. (1995). Super-
vised and unsupervised discretization of continuous
features. In International Conference Machine Learn-
ing — ICML’95, pages 194–202. Morgan Kaufmann.
Escolano, F., Suau, P., and Bonev, B. (2009). Information
Theory in Computer Vision and Pattern Recognition.
Springer.
Ferreira, A. and Figueiredo, M. (2011). Unsupervised joint
feature discretization and selection. In 5th Iberian
Conference on Pattern Recognition and Image Anal-
ysis - IbPRIA2011, pages LNCS 6669, 200–207, Las
Palmas de Gran Canaria, Spain.
Guyon, I. and Elisseeff, A. (2003). An introduction to vari-
able and feature selection. Journal of Machine Learn-
ing Research, 3:1157–1182.
Guyon, I., Gunn, S., Nikravesh, M., and Zadeh (Editors), L.
(2006). Feature Extraction, Foundations and Applica-
tions. Springer.
Guyon, I., Weston, J., and Barnhill, S. (2002). Gene se-
lection for cancer classification using support vector
machines. Machine Learning, 46:389–422.
Meyer, P., Schretter, C., and Bontempi, G. (2008).
Information-theoretic feature selection in microarray
data using variable complementarity. IEEE Journal
of Selected Topics in Signal Processing (Special Is-
sue on Genomic and Proteomic Signal Processing),
2(3):261–274.
Peng, H., Long, F., and Ding, C. (2005). Feature selec-
tion based on mutual information: Criteria of max-
dependency, max-relevance, and min-redundancy.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 27(8):1226–1238.
Saeys, Y., Inza, I., and Larra˜naga, P. (2007). A review of
feature selection techniques in bioinformatics. Bioin-
formatics, 23(19):2507–2517.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
468

Statnikov, A., Aliferis, C., Tsamardinos, I., Hardin, D.,
and Levy, S. (2005). A comprehensive evaluation
of multicategory classification methods for microar-
ray gene expression cancer diagnosis. Bioinformatics,
21(5):631–643.
Witten, I. and Frank, E. (2005). Data Mining: Practical
Machine Learning Tools and Techniques. Elsevier,
Morgan Kauffmann, 2nd edition.
FEATURE DISCRETIZATION AND SELECTION IN MICROARRAY DATA
469
