
PARALLEL IMPLEMENTATION AND COMPARISON OF
TWO UAV PATH PLANNING ALGORITHMS
Vincent Roberge, Mohammed Tarbouchi and Gilles Labonté
Department of Elec. and Comp. Eng., Royal Military College of Canada, Kingston, Canada
Keywords: UAV, Path planning, Genetic algorithm, Particle swarm optimization, Parallel implementation, T-test.
Abstract: The development of autonomous Unmanned Aerial Vehicles (UAVs) is of high interest to many
governmental and military organizations around the world. An essential aspect of UAV autonomy is the
ability for automatic path planning. In this paper, we use the genetic algorithm (GA) and the particle swarm
optimization algorithm (PSO) to cope with the complexity of the problem and compute feasible and quasi-
optimal trajectories for fixed wing UAVs in a complex 3D environment while considering the dynamic
properties of the vehicle. The characteristics of the optimal path are represented in the form of a multi-
objective cost function that we developed. The paths produced are composed of line segments, circular arcs
and vertical helices. We reduce the execution time of our solutions by using the “single-program, multiple-
data” parallel programming paradigm and we achieve real-time performance on standard COTS multi-core
CPUs. After achieving a quasi-linear speedup of 7.3 on 8 cores and an execution time of 10 s for both
algorithms, we conclude that by using a parallel implementation on standard multicore CPUs, real-time path
planning for UAVs is possible. Moreover, our rigorous comparison of the two algorithms shows, with
statistical significance, that the GA produces superior trajectories to the PSO.
1 INTRODUCTION
The path planner is an element of the UAV control
module (Chen et al., 2009). It allows the UAV to
autonomously compute the best path from a start
point to an end point. Whereas commercial airlines
fly constant prescribed trajectories, UAVs in
operational areas have to travel constantly changing
trajectories that depend on the particular terrain and
conditions prevailing at the time of their flight.
In the past, the best path has been associated with
the shortest path and deterministic search algorithms
were used to find the very shortest path. The
definition of the problem has since evolved and the
best path is now associated with the path that
minimizes the distance travelled, the average
altitude, the fuel consumption, the radar exposure,
etc. These are a few examples of the factors to be
considered and clearly show that the complexity of
the problem has grown. To cope with this
complexity, researchers have slowly moved from
using deterministic algorithms to using non-
deterministic algorithms (Masehian and
Sedighizadeh, 2007).
In this paper, we use two non-deterministic
algorithms to develop an operational path planning
module for fixed wing UAVs. Our research work
presents three important contributions. Firstly, we
propose a comprehensive cost function which
includes both the optimization and the feasibility
criteria. This allows us to use a generic optimization
algorithm (without modification) as the search
algorithm. In our case, we use the GA and the PSO,
but these could easily be replaced by other
algorithms. Secondly, we present a technique to
parallelize both the GA and the PSO while
minimizing the communication between the
processes in order to achieve a near linear speedup
and fully exploit the computing power of today’s
multicore CPUs. Finally, we offer a statistically
significant comparison between the quality of the
trajectories generated by our GA-based and PSO-
based path planners. Both algorithms have recently
been widely used for UAV path planning
(Pehlivanoglu, 2011), (Macharet et al., 2010), (Fu
and Gao, 2010), (Xia Li et al., 2010), (Bao et al.,
2010), (Yangguang Fu et al., 2009) and (Foo et al.,
2009). However, to our knowledge, there exists no
rigorous comparison between the two algorithms
162
Roberge V., Tarbouchi M. and Labonté G..
PARALLEL IMPLEMENTATION AND COMPARISON OF TWO UAV PATH PLANNING ALGORITHMS.
DOI: 10.5220/0003663501620167
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 162-167
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

when applied to this particular problem. The results
we present in this paper provide clear insight as to
which of the two optimization algorithms is
preferable for UAV path planning in complex 3D
environments.
2 REPRESENTATION
The first step of path planning is to discretize the
world space into a representation that will be
meaningful to the path planning algorithm. This
representation is closely related to a search
algorithm and some algorithms will only perform
well when coupled with a specific environment
representation. An overview of the performance of
different representations used with different
algorithms is presented in (Sariff and Buniyamin
2006). In our implementation (see Figure 1), we use
an approximate cell decomposition of the terrain
using a 2D grid where each element of the matrix
represents the elevation of the terrain. This
representation allows us to use digital elevation
maps freely available from the GeoBase (Anon n.d.)
repository with no further processing. Our
representation of the environment also allows for the
definition of cylindrical danger zones (or no-fly
zones) to be kept in a separate matrix where each
row represents the coordinates and the diameter of
the cylinder. Complex no-fly zones can be built by
partially juxtaposing multiple cylinders. The
trajectories generated by the optimization algorithm
are composed of line segments and encoded in a
matrix where each row represents the (x, y, z)
coordinates of a waypoint. The trajectories are flown
at constant speed and can also be represented as a
function of time.
Figure 1: Trajectory in a 3D environment.
3 COST FUNCTION
As previously stated, searching for the best path is
often associated with searching for the shortest path.
This is the case when solving the Traveling
Salesperson Problem (TSP), which consists of
finding the shortest path that visits all the given
cities only once. In the case of UAV path planning,
the optimal path is more complex and includes many
different characteristics. To take into account these
desired characteristics, a cost function is used and
the path planning algorithm becomes a search for a
path that will minimize the cost function. The cost of
a path decreases with the degree to which the desired
characteristics are being fulfilled. A path that fulfills
all the characteristics to a high degree would result
in a low cost. We define our cost function as
follows:
=
+
+
+
+
+
+
(1)
where C
length
penalizes longer paths, C
altitude
penalizes
paths with a higher average altitude, C
danger zones
penalizes paths going through danger zones, C
power
penalizes paths requiring more power than the
maximum available power of the UAV, C
collision
penalizes paths colliding with the ground, C
fuel
penalizes paths requiring more fuel than available in
the UAVs and finally, C
smoothing
penalizes paths that
cannot be smoothed using circular arcs. All terms
are normalized on the interval [0, 1]. C
length
, C
altitude
and C
danger zones
are optimization criteria and are used
to improve the quality of the trajectory whereas
C
power
, C
collision
, C
fuel
and C
smoothing
are feasibility
criteria that must be satisfied for the final trajectory
to be valid. In order to separate viable and non-
viable trajectories, we add a penalty constant to each
feasibility constraint not satisfied.
4 GENETIC ALGORITHM
The GA is a population based non-deterministic
optimization method that was developed by John
Holland in the 1960s and first published in 1975
(Holland, 1975). Based on the genetic theory of
Darwin evolution, the GA simulates the evolution of
a population of solutions to optimize a problem.
Similarly to living organisms adapting to their
environment over the generations, the solutions in
the GA adapt to a fitness function over an iterative
process using biology-like operators such as the
PARALLEL IMPLEMENTATION AND COMPARISON OF TWO UAV PATH PLANNING ALGORITHMS
163
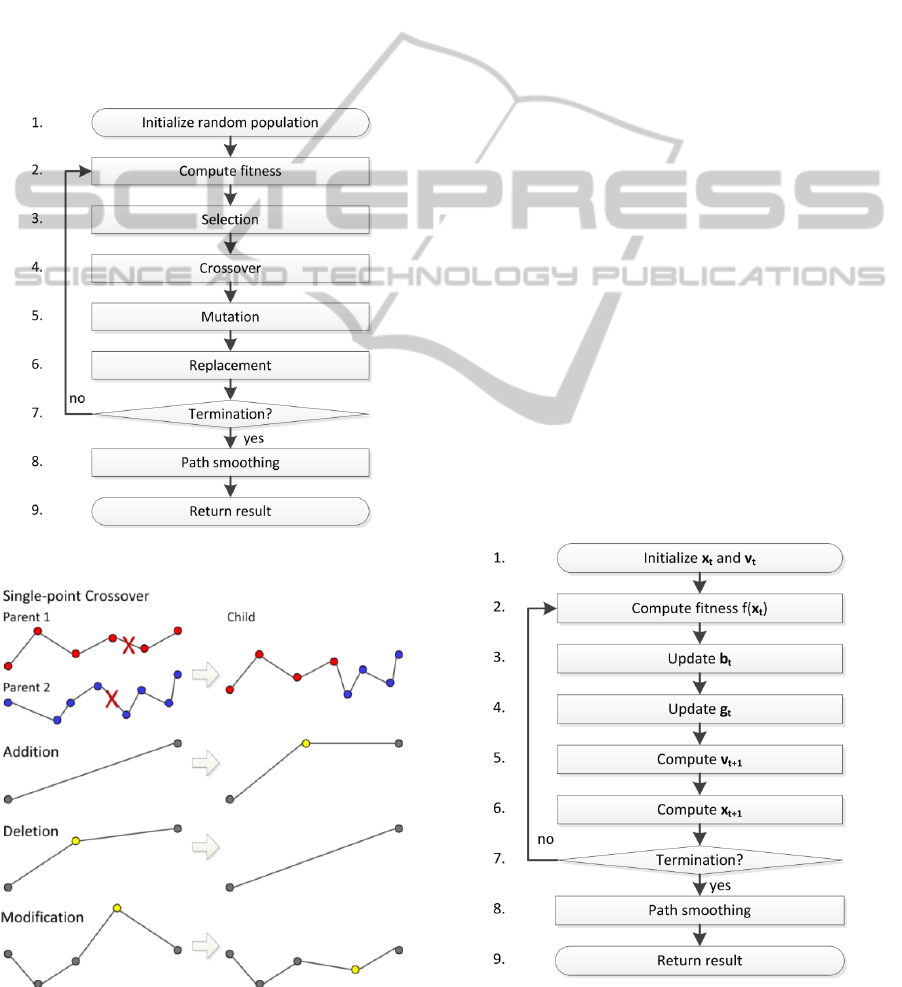
crossovers of chromosomes, the mutations of genes
and the inversions of genes. In this work, the GA
simulates the evolution of a population of
trajectories adapting to the cost function defined in
the previous section. Our implementation uses
stochastic universal sampling as the selection
method, single point crossover as the reproduction
mechanism and addition, deletion and modification
as genetic operators (Yu and Gen, 2010). We also
used the concept of elitism when replacing the old
generation with the new one in order to improve
conversion. The flowchart of the GA is shown in
Figure 2 and the different genetic operators used, in
Figure 3.
Figure 2: Flow chart of the genetic algorithm.
Figure 3: GA operators.
5 PARTICLE SWA RM
OPTIMIZATION
The PSO is a population based non-deterministic
optimization method that was proposed by Kennedy
and Eberhart in 1995 (Kennedy & Eberhart 1995).
The algorithm simulates the movement of a swarm
of particles in a multidimensional search space
progressing towards an optimal solution. The
position of each particle represents a candidate
solution (a complete trajectory encoded in a single
vector) and is randomly initiated. At every step of
the iterative process, the velocity of each particle is
individually updated based on the previous velocity
of the particle, the best position ever occupied by the
particle (personal influence) and the best position
ever occupied by any particle of the swarm (social
influence). As outlined in (Clerc 2005), the
equations used to compute the velocity and position
of a single particle at iteration are as follows:
=
+
.∗ (
−
)+
.∗ (
−
)
(2)
=
+
(3)
where variables in bold are vectors; v is the velocity
of the particle; x is its position; b is the best position
previously occupied by the particle; g is the best
position previously occupied by any particle of the
swarm; r
1
and r
2
are vectors of random values
between 0 and 1; and ω, c
1
and c
2
are the inertia, the
personal influence and the social influence
parameters. Still based on (Clerc, 2005), the flow
diagram of the PSO is displayed in Figure 4.
Figure 4: Flowchart of the particle swarm optimization.
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
164
6 PATH SMOOTHING
Consistent with solutions proposed in the literature
(Labonté, 2009), (Hasircioglu et al., 2008),
(Anderson et al., 2005), our solution generates a path
composed of line segments. This would be sufficient
for multi-directional ground robots, but inadequate
for a fixed-wing UAV. To remove all discontinuities
in the velocity, we smooth the final path by
connecting the line segments with simple circular
arcs (when the power available is sufficient) or
circles on a horizontal plateau (when the power
available is not sufficient to fly a simple circular arc)
based on (Labonté, 2009), (Anderson et al., 2005),
(Bottasso et al., 2008) and as shown on Figure 5.
Our final stage module also replaces any line
segment requiring more power than available with a
vertical helix as in (Labonté, 2009). Although
smoothing of the path is performed after the
optimization process, the feasibility of this operation
is verified in our cost function to ensure the
smoothing of the final trajectory is always possible.
Figure 5: Circular constructions used to smooth the final
trajectory and remove all discontinuity in the velocity (left
diagram shows a simple circular arc and the right diagram
shows a connection using 2 circular arcs and a circle on an
horizontal plane).
7 PARALLEL
IMPLEMENTATION
We have now discussed all the elements required to
build a complete path planning module for UAVs.
Although the generated trajectories are feasible and
nearly optimal, the computation time remains too
long for real-time applications. To address this
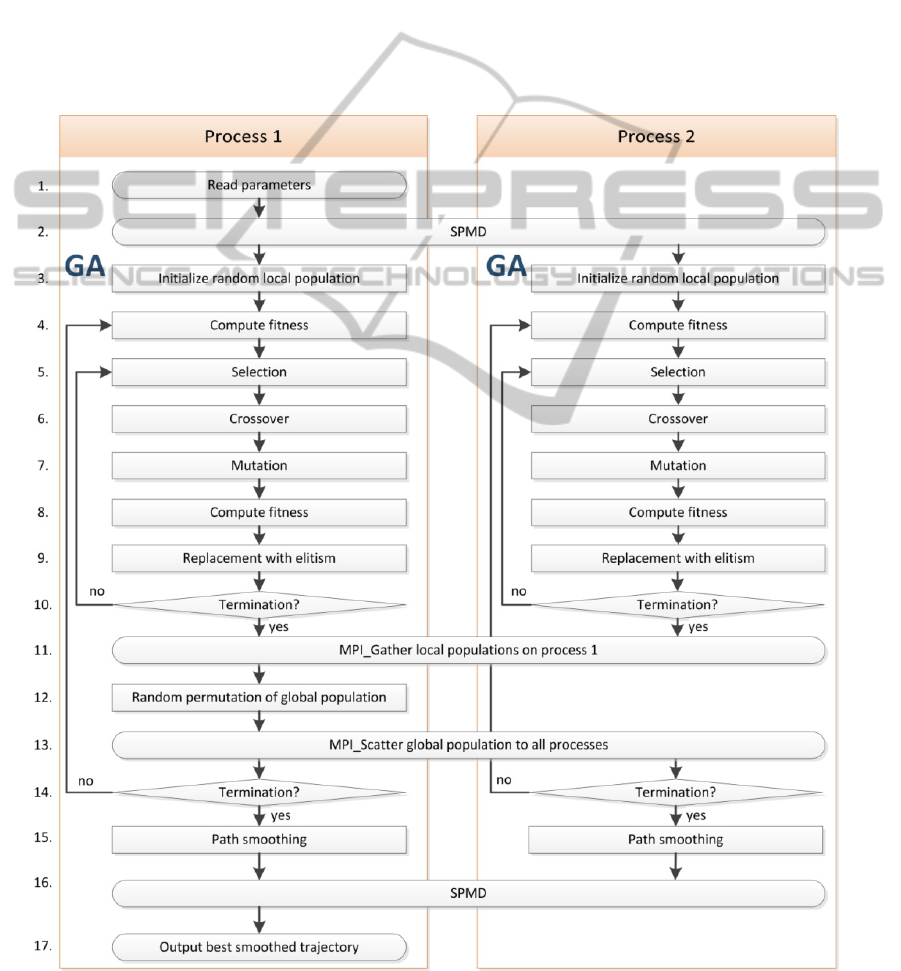
problem, we developed parallel versions of our GA
and PSO using the “Single-program, multiple-data”
parallel programming paradigm. Our
implementation was done in MATLAB. It minimises
the communication between the processes and
allows full use of today’s multicore CPUs. The
flowchart of our parallel GA is shown in Figure 10.
Although drawn for 2 processes, our implementation
allows any number of processes. Our parallel
version of the PSO is not shown in this paper but
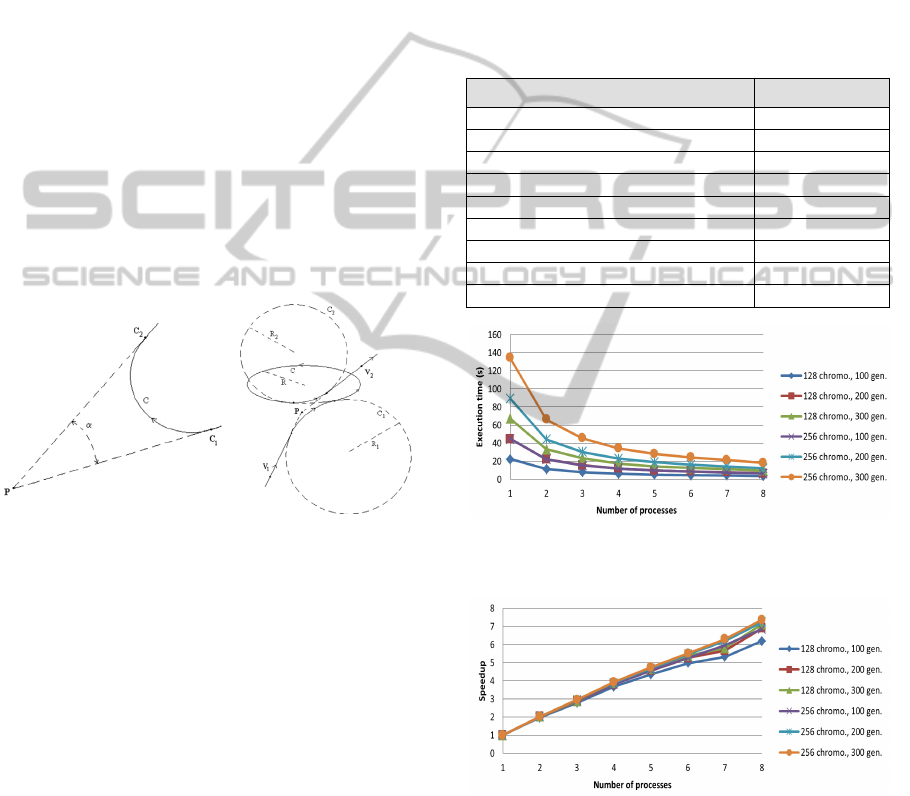
follows the same principle. The execution time and
the speedup of our parallel GA were measured on a
system equipped with two Intel Xeon E5310 quad-
core processors using the parameters in Table 1 and
are plotted in Figure 6 and Figure 7. The execution
time and the speedup of our parallel PSO are not
presented here, but are almost identical.
Table 1: Algorithm parameter values.
Parameters Values
Terrain resolution 500 x 500
Number of waypoints per trajectories 8
Number of gen. (AG) or ite. (PSO) 100, 200 and 300
Number of chromo. (AG) or part (PSO) 128 and 256
Mutation rate (AG) 10 %
Elitism rate (AG) 10 %
ω (PSO) 0.7298
c
1
(PSO) 1.4960
c
2
(PSO) 1.4960
Figure 6: Execution time of our parallel GA for different
work sizes.
Figure 7: Speedup achieved by our parallel GA for
different work sizes.
8 COMPARISON OF THE GA
AND THE PSO
Finally, we compare the performance of the GA and
the PSO using 40 different scenarios from two
PARALLEL IMPLEMENTATION AND COMPARISON OF TWO UAV PATH PLANNING ALGORITHMS
165
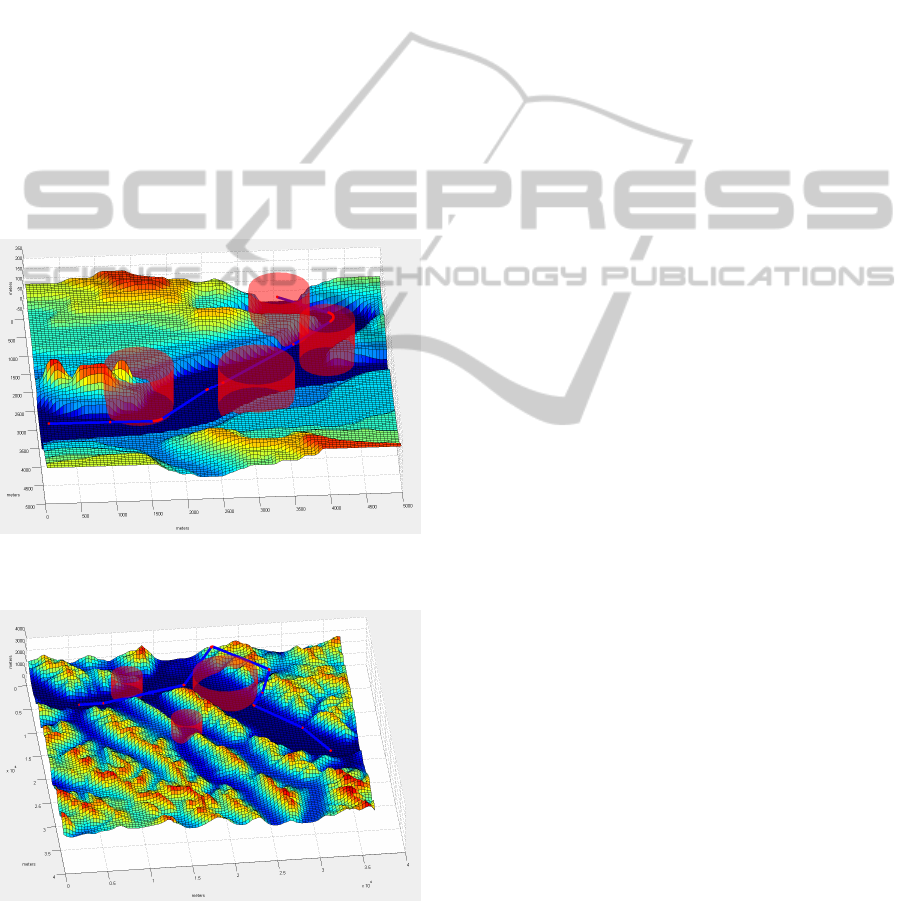
fictitious terrain elevation maps and six real terrain
elevation maps (see Figure 8 and Figure 9). The
digital elevation maps for the six real terrains were
taken from the GeoBase repository (Anon n.d.). The
average costs of 60 trajectories generated using our
parallel GA and parallel PSO are compared using
the T-test with 5% significance to conclude that:
The GA produced trajectories significantly better
than those generated by the PSO for 25 of the 40
scenarios;
the PSO produced trajectories significantly better
than those generated by the GA for 3 of the 40
scenarios; and
the GA and the PSO produced trajectory of similar
quality for 12 of the 40 scenarios.
Based on these results, we conclude that the GA is
preferable to the PSO when solving the path
planning problem for UAVs in a fixed computation
time of 10 s on multicore COTS processors.
Figure 8: 3D visualisation of the computed path (fictitious
map, 25 km
2
, altitude ranging from 0 to 250 m ASL).
Figure 9: 3D visualisation of the computed path (Banff,
Alberta, CA, 1 360 km
2
, 1 290 to 3 079 m ASL).
9 CONCLUSIONS
This paper presents a path planning solution for
UAVs which considers the dynamic properties of the
UAV and the complexity of a real 3D environment.
We used two non-deterministic algorithms, the GA
and the PSO, to attack this complexity and produce
solutions in a relatively short computation time. We
further reduced the execution time by developing
parallel versions of our algorithms. After achieving a
quasi-linear speedup of 7.3 on 8 cores and an
execution time of 10 s for both algorithms, we
conclude that by using a parallel implementation on
standard multicore CPUs, real-time path planning
for UAVs is possible. Moreover, our rigorous
comparison of the two algorithms shows, with
statistical significance, that the GA produces
superior trajectories to the PSO.
REFERENCES
Anderson, E. P., Beard, R. W. & McLain, T. W., 2005.
Real-time dynamic trajectory smoothing for unmanned
air vehicles. IEEE Transactions on Control Systems
Technology, pp.471-7.
Anon, GeoBase - Canadian Digital Elevation Data.
Available at: http://www.geobase.ca/geobase/en/
data/cded/index.html;jsessionid=E999310F1B8F4087
A4913460B9E5EE47 [Accessed January 27, 2011a].
Bao, Y., Fu, X. & Gao, X., 2010. Path planning for
reconnaissance UAV based on particle swarm
optimization. CINC 2010. Wuhan, China, pp. 28-32.
Bottasso, C. L., Leonello, D. & Savini, B., 2008. Path
planning for autonomous vehicles by trajectory
smoothing using motion primitives. IEEE
Transactions on Control Systems Technology,
pp.1152-1168.
Chen, H., Wang, X.-min & Li, Y., 2009. A Survey of
Autonomous Control for UAV. In 2009 International
Conference on Artificial Intelligence and
Computational Intelligence - Volume 2. pp. 267-271.
Clerc, M., 2005. Particle Swarm Optimization, France:
Lavoisier.
Foo, J.L. et al., 2009. Path planning of unmanned aerial
vehicles using B-splines and particle swarm
optimization. Journal of Aerospace Computing,
Information and Communication, pp.271-290.
Fu, X. & Gao, X., 2010. Genetic algorithm with adaptive
immigrants for dynamic flight path planning. In 2010
IEEE ICIS. Xiamen, China, pp. 630-634.
Hasircioglu, I., Topcuoglu, H. R. & Ermis, M., 2008. 3-D
path planning for the navigation of unmanned aerial
vehicles by using evolutionary algorithms. In 10th
annual conference on Genetic and evolutionary
computation. Atlanta, USA, pp. 1499-1506.
Holland, J. H., 1975. Adaptation in Natural and Artificial
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
166
Systems, MIT Press.
Kennedy, J. & Eberhart, R., 1995. Particle swarm
optimization. In IEEE International Conference on
Neural Networks. Perth, Australia, pp. 1942-1948.
Labonté, G., 2009. Sur la Construction de trajectoires
dynamiquement réalisables pour les avions à partir de
suites de segments de droites, 2e version.
Li, Xia et al., 2010. A three dimensional path planning for
unmanned air vehicle based on improved genetic
algorithm. Xibei Gongye Daxue Xuebao/Journal of
Northwestern Polytechnical University, pp.343-348.
Macharet, D. G., Neto, A. A. & Campos, M. F. M., 2010.
Feasible UAV Path Planning Using Genetic
Algorithms and Bezier Curves. 20th Brazilian
Symposium on Artificial Intelligence. Berlin,
Germany: Springer Verlag, pp. 223-32.
Masehian, E. & Sedighizadeh, D., 2007. Classic and
Heuristic Approaches in Robot Motion Planning - A
Chronological Review.
Pehlivanoglu, Y. V., 2011. A new vibrational genetic
algorithm enhanced with a Voronoi diagram for path
planning of autonomous UAV.
Sariff, N. & Buniyamin, N., 2006. An overview of
autonomous mobile robot path planning algorithms. In
2006 4th Student Conference on Research and
Development. NJ, USA, pp. 183-8.
Yangguang Fu et al., 2009. Path planning for UAV based
on quantum-behaved particle swarm optimization. In
MIPPR. USA. p. 74970B.
Yu, X. & Gen, M., 2010. Introduction to Evolutionary
Algorithms, London: Springer.
Figure 10: Flowchart of our parallel genetic algorithm.
PARALLEL IMPLEMENTATION AND COMPARISON OF TWO UAV PATH PLANNING ALGORITHMS
167
