
AUTOMATIC ESTIMATION OF THE LSA DIMENSION
Jorge Fernandes, Andreia Art
´
ıfice and Manuel J. Fonseca
Department of Computer Science and Engineering, INESC-ID/ IST/ Technical University of Lisbon
R. Alves Redol, 9, 1000-029 Lisboa, Portugal
Keywords:
LSA, LSA dimension, Unsupervised text classification, Bootstrapping.
Abstract:
Nowadays the size of collections of information achieved considerable sizes, making the finding and explo-
ration of a particular subject hard to achieve. One way to solve this problem is through text classification,
where a theme or category is assigned to a text based on the analysis of its content. However, existing ap-
proaches to text classification require some effort and a high level of knowledge on this subject by the users,
making them inaccessible to the common user. Another problem of current approaches is that they are op-
timized for a specific problem and can not easily be adapted to another context. In particular, unsupervised
methods based on the LSA algorithm require users to define the dimension to use in the algorithm. In this
paper we describe an approach to make the use of text classification more accessible to common users, by
providing a formula to estimate the dimension of the LSA based on the number of texts used during the boot-
strapping process. Experimental results show that our formula for estimation of the LSA dimension allows us
to create unsupervised solutions able to achieve results similar to supervised approaches.
1 INTRODUCTION
Text classification consists in assigning a category
(from a set of predefined categories) to a text, based
on its content. Although this problem dates from the
60s, it still is relevant since the amount of (uncata-
logued) information increases everyday. Information
such as, RSS feeds, news, scientific papers, e-books,
etc., need to be organized and cataloged to make life
easier for users.
Nowadays when we want to classify a set of texts
we can either resort to supervised, unsupervised or
even hybrid approaches. While supervised solutions
require the manual classification of a set of texts, un-
supervised approaches avoid that by using a boot-
strapping method to perform a first classification of
unclassified texts. The classified texts (in both ap-
proaches) are then used to train a classifier, which will
be later used to classify other texts.
Various unsupervised approaches use the Latent
Semantic Analysis (LSA) (Landauer et al., 1998) al-
gorithm to perform feature extraction from the texts.
Since one of the main characteristics of the LSA algo-
rithm is its dimension, the selection of this value is of
crucial importance because it affects the final results
of the classification. However, from the literature we
did not find any founded choice for its value, being its
selection made by skilled people, according to the ac-
tual context of the problem and after several iterations
to optimize the final results.
In this paper we propose an empirical formula to
automatically estimate the best value for the LSA di-
mension, according to the current context of the prob-
lem, namely the number of documents used during
the bootstrapping step. We applied this formula to es-
timate the LSA dimension of an unsupervised system
and compare the classification results with a super-
vised solution. Experimental evaluation show that the
results are similar, with the advantage of not requiring
any input from the users beside the set of texts to be
used by the bootstrapping algorithm.
The remainder of this paper is organized as fol-
lows. Section 2 provides a summary of the supervised
and unsupervised approaches for text classification.
In Section 3 we present our solution for the automatic
estimation of the LSA dimension and in Section 4 we
present the results of the experimental evaluation. Fi-
nally, in Section 5 we conclude the paper.
2 RELATED WORK
Most of the existing text classification techniques can
be grouped into two groups: supervised learning and
unsupervised learning.
309
Fernandes J., Artífice A. and J. Fonseca M..
AUTOMATIC ESTIMATION OF THE LSA DIMENSION.
DOI: 10.5220/0003666103010305
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 301-305
ISBN: 978-989-8425-79-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

Supervised Learning requires a manual classifica-
tion of a group of texts into a predefined set of cate-
gories. This result is then used to train and build an
automatic classifier able to categorize any text into the
predefined set of categories.
According to (Huang, 2001), there are two key
factors for a successful supervised learning. One is
the feature extraction, which should accurately rep-
resent the contents of text in a compact and efficient
manner, and the other is the classifier design, which
should take the maximum advantage of the proper-
ties inherent to the texts, to achieve the best possi-
ble results. Huang studied several algorithms for both
factors, and concluded that the LSA algorithm is the
most appropriated for the feature extraction, and the
SVM for the classifier.
(Debole and Sebastiani, 2003) and (Ishii et al.,
2006) both agree with Huang in using the LSA for
feature extraction, but they introduced some changes
to the feature extraction process. While the first au-
thors included a number of “supervised variants” of
TFIDF weighting, the second authors complemented
the LSA by introducing the concept of data grouping.
Although supervised learning can obtain good re-
sults, they require a large number of texts (literature
values vary between 500 and 1400) and a manual clas-
sification to train the final classifier.
Unsupervised Learning tries to overcome the dis-
advantages of the supervised approaches by replacing
the manual classification of a high number of texts
with an automatic classification (often called boot-
strapping). By doing so we are able to greatly reduce
the costs and the need for human intervention.
Unfortunately the automatic classification of texts
used by the unsupervised learning can cause vari-
ous misclassification, introducing noise in the training
of the classifier and affecting its final performance,
which traditionally is worst than in the supervised
learning.
Since most unsupervised approaches requires a
list of representative keywords for each category,
some authors tried to improve the bootstrapping qual-
ity by developing algorithms to help in the selection
of the best keywords for each category. (Liu et al.,
2004) used a clustering algorithm to identify the most
important words for each cluster of texts. Then the
user could inspect the ranked list and select a small
set of representative keywords for each category.
(Barak et al., 2009) went a step forward by com-
pletely automating the process. Their approach at-
tempts to automatically extract possible keywords us-
ing only the category name as a starting point. The
authors introduced also a novel scheme that mod-
els both lexical references, based on certain relations
present in WordNet and Wikipedia, and contextual
references, using the model of the LSA. From the re-
sulting model they extract the necessary keywords.
(Gliozzo et al., 2005) tried to minimize the num-
ber of misclassifications of the bootstrapping by first
preprocessing the text to remove all the words that are
not nouns, verbs, adjectives and adverbs. The result-
ing set of words is then represented using LSA. An
algorithm based on unsupervised estimation of Gaus-
sian Mixtures is then applied to differentiate between
relevant and non-relevant information using statistics
from unclassified texts. According to the authors a
SVM classifier trained with the results from this boot-
strapping algorithm achieved results comparable to a
supervised solution.
In summary, although supervised learning ap-
proaches present the best results, they require some-
one (an expert person) to manually classify a large
number of texts, which is an arduous and monotonous
task, with an enormous cost associated. On the other
hand, the unsupervised learning avoids the manual
classification by including a bootstrapping technique,
but requires specific knowledge about the algorithms
in use (e.g. LSA) and of the domain problem. In-
deed, when we use an approach that reduce the di-
mension of the features extracted from the text, like
for instance the LSA algorithm the selection of the
dimension is very important, since its value affects
the final results. From the analysis of the several ex-
isting proposals based on the LSA algorithm, we did
not find a clear explanation on how to choose the best
dimension for the LSA. In most cases its value is cho-
sen after several iterations and taking into account the
specific context of the current problem.
To overcome this, to minimize the human inter-
vention, and to offer good results, we propose in this
paper a solution to automatically estimate the “opti-
mum” dimension for the LSA algorithm, taking into
account only the number of texts.
3 LSA DIMENSION ESTIMATION
The solution that we developed for the bootstrapping
step starts by reducing the size of the vocabulary by
removing useless words that only introduce noise in
the categorization. We remove words contained into
a stopwords list and the least frequent words (words
that appeared less than three times)(Joachims, 1997).
By removing the least frequent words we are able to
eliminate typos and reduce the noise of the vocabu-
lary. Additionally, by reducing the size of the vocab-
ulary we will reduce the complexity of the problem
and the computational cost of all the following algo-
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
310
rithms.
To represent the content of the texts we used the
LSA. We built a word-document matrix by grouping
the individual document representations and applied
a TFIDF (Salton and Buckley, 1988) to the result-
ing frequency matrix, followed by SVD (Berry, 1992)
to obtain the new matrices of reduced dimensionality.
The reduced dimension of the resulting space need to
be carefully selected (as we will see below) to fit well
the problem to be solved. Then, the resulting latent
semantic space is used to classify the documents and
this classification is used to train the classifier.
To get satisfactory results the dimension of the
LSA algorithm must be selected appropriately. Typi-
cally this value is selected empirically, based on val-
ues used on other similar problems, or through vari-
ous tests to identify the interval where the optimum
value of the dimension is. This represents a problem,
because an ordinary person does not have the knowl-
edge to make this selection, and also because we can
not use a fixed value. Here, we propose a solution that
will allow ordinary people to use the LSA algorithm
in various problem contexts, by defining a formula for
the estimation of the most appropriated LSA dimen-
sion based on the context of the problem. To that end,
we analyzed the behavior of the LSA and performed
several experimental tests.
From the literature, we found that the LSA’s per-
formance increases as the number of dimensions also
increases, until reaching a maximum. After that
value, any further increase in the number of dimen-
sions will only decrease the performance. Moreover,
if we look carefully into the LSA algorithm we can
see that the number of dimensions is affected by the
size of the vocabulary and by the number of texts used
to extract the features. Since the size of the vocab-
ulary is somehow directly related to the number of
texts, we can assume that the number of dimensions
depends exclusively from the number of texts.
Based on this we performed a set of experimen-
tal studies to identify the range of dimension values
where the performance has a maximum, and tried to
figure out a formula to estimate a value for the dimen-
sion within that interval.
To perform the experimental tests we considered
various context problems, where we had ten cate-
gories (Science and Technology, Cinema and TV,
Sport, Economy and Management, Informatics and
Internet, Games, Music, Politics, Health, and Motor
Vehicles), with distinct characteristics among them,
and three number of texts per category (32, 64 and
128). Texts were collected from news sites, and their
sizes vary from a few paragraphs to one to two pages.
For each problem context we performed five in-
dividual tests using five different sets of texts (in the
same conditions) and measured the F1-measure. The
final result for a specific context is the average of the
F1-measure from the five individual tests.
The values of the dimension used to compute the
F1-measure were selected to figure out if the opti-
mum value for the dimension varies linearly or non-
linearly. To that end we considered the following val-
ues for the dimension:
√
n
T
, 2
√
n
T
, 3
√
n
T
,
1
5
n
T
and
1
3
n
T
, where n
T
represents the number of texts.
We first studied the performance for 32 texts per
category (320 texts in total), and we achieved the val-
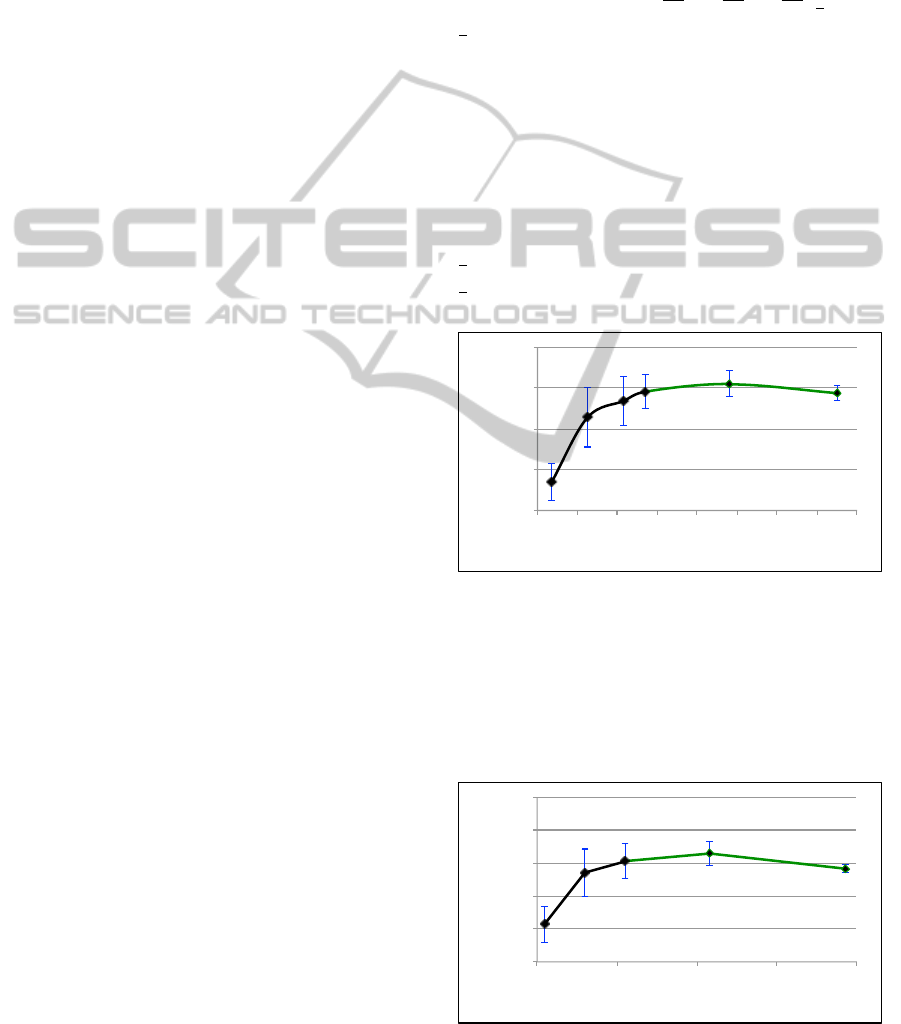
ues depicted in Figure 1. As we can see we have a
maximum for 106 dimensions. It is important to high-
light that this does not mean that the optimum value
for the dimension is 106, but that the F1-measure in-
creases and then decreases, with the optimum value
inside the interval ]64, 160[. In this particular case,
we also computed the F1-measure for a dimension of
1
2
n
T
because the F1-measure was still increasing at
1
3
n
T
.
!"#
$%#
%$#
&'#
!(&#
!&(#
&()#
"()#
*()#
+()#
!(()#
!(# $(# %(# "(# +(# !!(# !$(# !%(# !"(#
!"#$%&'()%*
+($,%)*-.*/0$%1'0-1'*
Figure 1: LSA performance for a set of 320 texts.
For the next test we used 64 texts per category
(640 texts in total), and we achieved the values de-
picted in Figure 2. As we can see we achieved a max-
imum for 128, and the interval for the optimum value
is ]75, 213[.
!"#
"$#
%"#
&!'#
!&(#
%")#
'$)#
'")#
*$)#
*")#
&$$)#
!$# %$# &!$# &%$# !!$#
!"#$%&'()%*
+($,%)*-.*/0$%1'0-1'*
Figure 2: LSA performance for a set of 640 texts.
AUTOMATIC ESTIMATION OF THE LSA DIMENSION
311
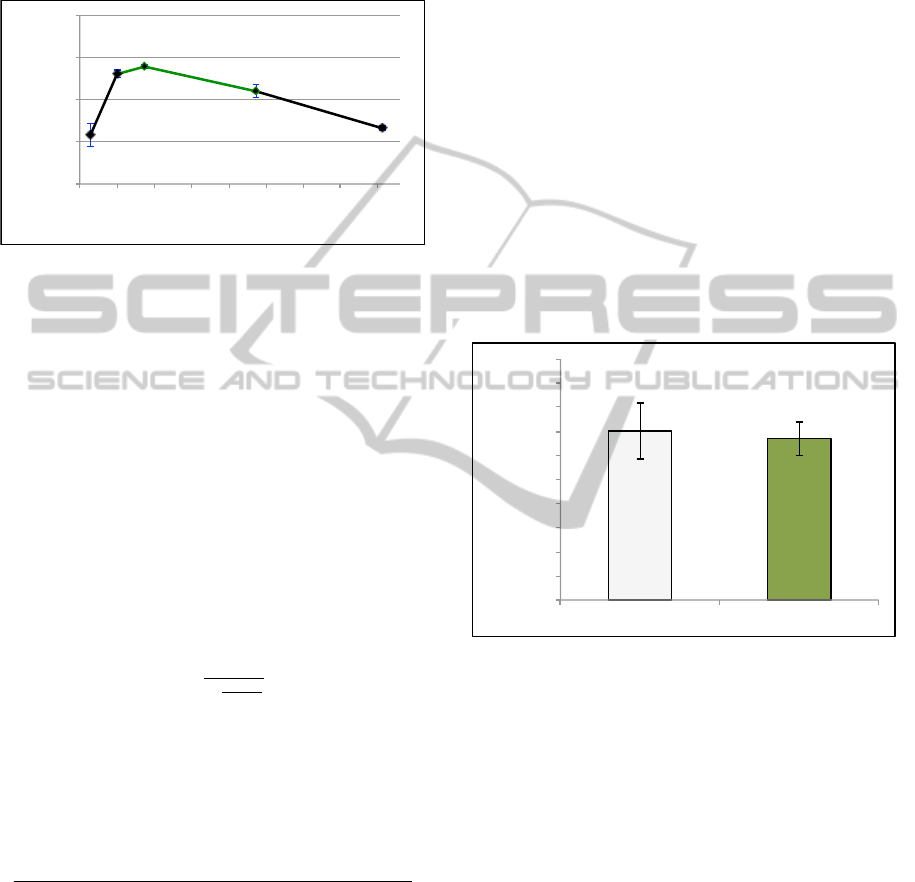
Finally, we used 128 texts per category (1280 texts
in total), producing the results depicted in Figure 3. In
this case we have a maximum for 107 dimensions and
an interval for the optimum value between ]71, 256[.
!"#
$%#
%&$#
'"(#
)'(#
*&+#
*"+#
,&+#
,"+#
%&&+#
'&# $&# %'&# %$&# ''&# '$&# !'&# !$&# )'&#
!"#$%&'()%*
+($,%)*-.*/0$%1'0-1'*
Figure 3: LSA performance for a set of 1280 texts.
By analyzing the obtained data, the first conclu-
sion that we can take is that the number of dimensions
does not grow linearly with the number of texts. In-
deed, while the number of texts increase the number
of dimensions corresponds to a smaller percentage of
the total number of texts. In the first case (320 texts)
the optimum value is between 20% and 50% of the
number of texts, in the second case (640 texts) is be-
tween 12% and 33%, and in the last case (1280 texts)
is between 6% and 20%.
After looking at various mathematical functions
we identified the square root as the one with the most
similar behavior. Based on that we studied some pos-
sibilities and achieved the following formula for the
estimation of the LSA dimension:
k = n
1
1+
log(n
T
)
10
!
T
(1)
where n
T
is the number of texts.
If we now apply this formula to the previous three
cases we obtain the following values:
Table 1: Intervals for the optimum values of dimension, and
the values automatically estimated using equation 1.
# Texts Expected interval Estimated Value
320 ]64, 160[ 100
640 ]75, 213[ 155
1280 ]71, 256[ 235
As we can see all the estimated values belong to
the interval where the optimum value is. Moreover,
the literature mentioned that for problems where we
have more than 20000 texts the typical value recom-
mended for the dimension is between 200 and 2000.
Though, we can conclude that our formula estimates
values inside that interval.
4 EXPERIMENTAL EVALUATION
To evaluate our formula for the estimation of the ap-
propriate dimension for the LSA, we compared the re-
sults achieved by a classifier trained with the classifi-
cation produced by our bootstrapping algorithm and a
classifier trained using texts classified manually. Our
goal was to check if our solution, where the over-
all bootstrapping step was automatized with the in-
clusion of the estimation of the LSA dimension, can
compete with a supervised solution, where exist a lot
of human intervention.
To perform the tests, we used the same set of texts
in both solutions, supervised and unsupervised. Then,
we compared the two classifiers using two distinct sit-
uations. One where we used 500 texts to train the
classifiers and 1000 for evaluation, and another where
we used 1000 texts to train and 500 for evaluation. In
both situations the two sets were disjoints.
!"#$
%!#$
!"#
$!"#
%!"#
&!"#
'!"#
(!"#
)!"#
*!"#
+!"#
,!"#
$!!"#
&'()*+,-).$ /0-'()*+,-).$
1234)5-'*)$
Figure 4: Performance results for supervised and unsuper-
vised solutions, using 500 texts to train and 1000 texts for
recognition.
Figure 4 shows the results achieved by both solu-
tions for the first situation, while Figure 5 presents
the results for the second case. As we can see in
both cases our approach presents results similar to
the supervised solution. In the first case we have a
F1-measure of 67% against 70% an in the second we
have 84% against 85%. Although in both cases the
F1-measure is smaller for the unsupervised solution,
the standard deviations intersect, meaning that our ap-
proach can achieve results comparable to supervised
solutions without their costs.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
312
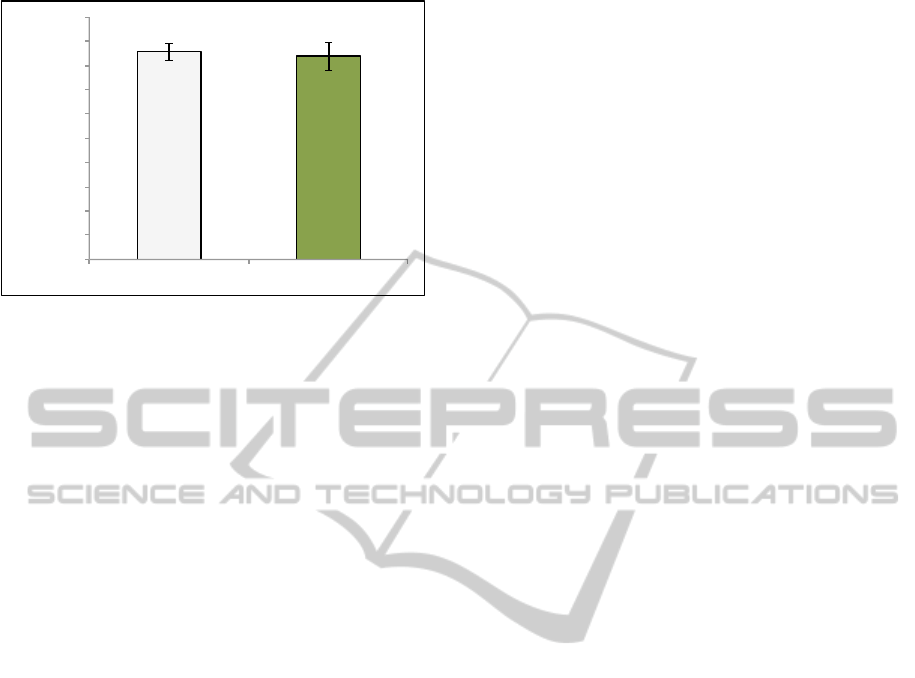
!"#$
!%#$
!"#
$!"#
%!"#
&!"#
'!"#
(!"#
)!"#
*!"#
+!"#
,!"#
$!!"#
&'()*+,-).$ /0-'()*+,-).$
1234)5-'*)$
Figure 5: Performance results for supervised and unsuper-
vised solutions, using 1000 texts to train and 500 texts for
recognition.
5 CONCLUSIONS
As we have seen unsupervised solutions have a boot-
strapping step where, in the majority of the cases, a
LSA algorithm is used. However, to properly take ad-
vantage of the LSA a good selection of its dimension
is crucial. In this paper we presented a solution, based
on a set of empirical studies, to automatically estimate
the most appropriated dimension for the LSA. By pro-
viding this estimation mechanism, we will allow peo-
ple without specific knowledge about the LSA algo-
rithm to use it parameterized with the correct values
to assure a good performance.
Indeed, from the experimental evaluation we can
conclude that our formula allows unsupervised solu-
tions based on the LSA to achieve results similar to
supervised methods.
ACKNOWLEDGEMENTS
This work was supported by FCT through the
PIDDAC Program funds (INESC-ID multiannual
funding) and the Crush project, PTDC/EIA-
EIA/108077/2008.
REFERENCES
Barak, L., Dagan, I., and Shnarch, E. (2009). Text catego-
rization from category name via lexical reference. In
NAACL ’09: Proceedings of Human Language Tech-
nologies: The 2009 Annual Conference of the North
American Chapter of the Association for Computa-
tional Linguistics, Companion Volume: Short Papers,
pages 33–36, Morristown, NJ, USA. Association for
Computational Linguistics.
Berry, M. (1992). Large scale sparse singular value compu-
tations. International Journal of Supercomputer Ap-
plications, 6:13–49.
Debole, F. and Sebastiani, F. (2003). Supervised term
weighting for automated text categorization. In Pro-
ceedings of SAC-03, 18th ACM Symposium on Applied
Computing, pages 784–788. ACM Press.
Gliozzo, A., Strapparava, C., and Dagan, I. (2005). Inves-
tigating unsupervised learning for text categorization
bootstrapping. In HLT ’05: Proceedings of the confer-
ence on Human Language Technology and Empirical
Methods in Natural Language Processing, pages 129–
136, Morristown, NJ, USA. Association for Computa-
tional Linguistics.
Huang, Y. (2001). Support vector machines for text catego-
rization based on latent semantic indexing. Technical
report, Electrical and Computer Engineering Depart-
ment, The Johns Hopkins University.
Ishii, N., Murai, T., Yamada, T., and Bao, Y. (2006).
Text classification by combining grouping, lsa and
knn. In ICIS-COMSAR ’06: Proceedings of the 5th
IEEE/ACIS International Conference on Computer
and Information Science and 1st IEEE/ACIS Interna-
tional Workshop on Component-Based Software Engi-
neering,Software Architecture and Reuse, pages 148–
154, Washington, DC, USA. IEEE Computer Society.
Joachims, T. (1997). A probabilistic analysis of the rocchio
algorithm with tfidf for text categorization. In ICML
’97: Proceedings of the Fourteenth International Con-
ference on Machine Learning, pages 143–151, San
Francisco, CA, USA. Morgan Kaufmann Publishers
Inc.
Landauer, T., Foltz, P., and Laham, D. (1998). An intro-
duction to latent semantic analysis. In Discourse Pro-
cesses, pages 259–284.
Liu, B., Li, X., Lee, W., and Yu, P. (2004). Text classifica-
tion by labeling words. In AAAI’04: Proceedings of
the 19th national conference on Artifical intelligence,
pages 425–430. AAAI Press.
Salton, G. and Buckley, C. (1988). Term-weighting ap-
proaches in automatic text retrieval. Information Pro-
cessing and Management, 24(5):513–523.
AUTOMATIC ESTIMATION OF THE LSA DIMENSION
313
