EPILEPTIC ELECTROENCEPHALOGRAM SIGNAL
CLASSIFICATION BASED ON SPARSE REPRESENTATION
Jing Wang
1,2
and Ping Guo
1
1
Laboratory of Image Processing and Pattern Recognition, Beijing Normal University, Beijing, 100875, China
2
School of Foundational Education, Peking University Health Science Center, Xueyuan Rd, Beijing, China
Keywords: Electroencephalogram (EEG) signals, Epilepsy seizures, Seizure detection, Overcomplete dictionary, Sparse
representation, Bayesian decision rule.
Abstract: Epilepsy seizure detection in Electroencephalogram (EEG) is a major issue in the diagnosis of epilepsy and
it can be considered as a classification problem. According to the particular property of EEG, a novel
method based on sparse representation is proposed for epilepsy detection in this paper. Classification accu-
racy, robustness on noisy data and parameters (the size of dictionary and the number of features) of pro-
posed method are tested and analysed on the public available data. The proposed method can obtain the
highest classification accuracy among the discussed methods when the suitable parameters are set, and the
proposed method based on sparse representations for classification is robust to noise. This is consistent with
the theory that sparse representations can capture the inherent structure of signal. Furthermore, it is shown
by experiments that the optimal selection of the parameters is critical to the performance of epilepsy detec-
tion.
1 INTRODUCTION
Epilepsy is a chronic neurological disorder that
plagues about 50 million people worldwide at one
time. It is characterized by recurrent unprovoked
seizures that disturb the nervous system. However
who has a seizure does not necessarily have epi-
lepsy, for example many diseases might cause sei-
zure-like activity such as stroke, life-threatening
dehydration or high temperature. And sometimes
there authentically are epileptic even absence of
seizures. Due to that non-epileptic seizures are diffi-
cult to differentiate from epileptic ones, misdiagno-
sis might happen. A significant way for identifying
and analyzing epileptic seizure activity in humans is
by using Electroencephalogram (EEG) signals,
which record the electrical potentials produced by
the brain, and are the basis of epilepsy clinical diag-
nosis and treatment. In the past, interpretation of the
EEG was limited to visual inspection by a neuro-
physiologist, an individual trained to make qualita-
tively a distinction between normal EEG activity and
abnormalities contained within EEG records. Unfor-
tunately, prediction of epilepsy which needs visual
inspection of long recordings of EEG is usually a
time-consuming and high-cost process. Therefore,
several diagnostic aid approaches for automated
detecting epileptic seizures from EEG signals were
proposed in recent years.
Nigam and Graupe employed a multistage
nonlinear pre-processing filter for extracting two
features: relative spike amplitude and spike
occurrence frequency, then which were fed to a
diagnostic artificial neural network for automatically
detecting of epileptic seizures from EEG signals and
obtained 97.2% accuracy (Nigam, 2004). Srinivasan
obtained 99.6% classification accuracy by using
Time & Frequency domain features and recurrent
neural network (Srinivasan, 2005). Güler et al
obtained 96.79% classification accuracy by using
recurrent neural networks to detect the epileptic
seizure from EEG signals (Güler, 2005). Subasi
decomposed the EEG signals using discrete wavelet
transform. Some statistical information were
extracted from the wavelet coefficients, and applied
for different classifiers for epileptic EEG
classification, such as feed-forward error back-
propagation artificial neural network (FEBANN)
(Subasi, 2005-A), dynamic wavelet network (DWN)
(Subasi, 2005-B), dynamic fuzzy neural network
(DFNN) (Subasi, 2006), an adaptive neuron-fuzzy
inference system (ANFIS) (Subasi, 2007-A) and
15
Wang J. and Guo P..
EPILEPTIC ELECTROENCEPHALOGRAM SIGNAL CLASSIFICATION BASED ON SPARSE REPRESENTATION.
DOI: 10.5220/0003667100150023
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 15-23
ISBN: 978-989-8425-84-3
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

mixture of expert system (ME) (Subasi, 2007-B),
and separately obtained accuracies of 91%, 93%,
93%, 94% and 95%, respectively.
Übeyli employed wavelet analysis with
combined neural network model to discriminate
EEG signals (Übeyli, 2009). The EEGs were
decomposed into time–frequency representations
using discrete wavelet transform (DWT) and then
statistical feature were calculated. Then a two-level
neural network model was used to classify three
types of EEG signals. classification accuracy of
94.83% was achieved. Ocak detected epileptic
seizures based on approximate entropy (ApEn) and
discrete wavelet transform. EEG signals were firstly
decomposed into approximate and detailed
coefficients by DWT, and then ApEn values for each
set of coefficients were computed. Finally, surrogate
data analysis was used to classify the ApEn values
(Ocak, 2009).
EEG is a non-stationary and extremely sensitive
signal, even a small movement from eyes or body
can contaminate it. Most of researches extract
features for classification from signals in which the
polluted signal segments or contaminated channels
have been removed by visual inspection and the
noise influences from EOG, EMG and other
channels have been reducing by preprocessing, and
don’t consider the influence of noise to classification
accuracies.
Recent research suggests that sparse
representation of signal over complete dictionaries is
a powerful representation method for processing
signal and images, and it is applied in many fields.
Sparse representations have also been used for face
recognition (Wright, 2009), signal classifi-cation
(Huang, 2007). However, to our knowledge, there is
no study related to sparse representation in epileptic
EEG signal classification till now. In this paper, a
new approach based on sparse represen-tation is
presented for epileptic EEG signal classification.
Features for classification are extracted by sparse
representation of original EEG signal directly, and
this decrease the run time for data preprocessing is
not needed. Since sparse representation can capture
the inherent structures of signal, the proposed
method is relative robust to some noise. The
feasibility and efficiency of the proposed method are
shown by the experiments.
This paper is structured as follows: theoretical
background is introduced in section II, and in section
III EEG signal classification based on sparse
representation is proposed, Then Section IV presents
the experimental results. Finally, conclusions and
future work are discussed.
2 THEORETICAL
BACKGROUND
2.1 Sparse Representations of Signals
Some natural signals have compact and condense
representation in some domain, the property which
is called sparsity (Richard, 2007). A real-valued,
finite-length, one-dimensional, discrete-time signal x
can be viewed as an N×1 column vector in R
N
. Any
signal in R
N
can be represented in term of a basis of
N×1 orthonormal vectors {D
i
}
i=1
N
. It can be formu-
lated as follow:
x= α
i
D
i
N
i=1
or x=Dα. (1)
Where, α is the N×1 column vector of weighting
coefficients. Here, x and α are equivalent representa-
tions of the signal, with x is in the time domain and
α is in the D domain.
The signal x is K-sparse if it is a linear combina-
tion of only K (K<<N) basis vectors: that is, only K
of the coefficients in equation (1) are nonzero (or
large) and (N-K) are zeros (or small). So the sparse
representation of signal can use as little as possible
amount of data to represent the original data.
2.2 Gabor Dictionary
In sparse representation, the selection of domain D is
very important, only appropriate basis can ensure the
sparsity of signal. Recent years, the sparse represen-
tation of signal based on overcomplete redundant
dictionaries has been attracting increasing attention.
That signal were decomposed with an overcomplete
dictionary instead of an orthonormal basis can result
in not only a higher sparsity degree, but also greater
flexibility in capturing the inherent structure of the
natural signals (Zhang, 2005). An overcomplete
dictionary can either be chosen as a prespecified set
of functions such as overcomplete wavelets,
curvelets, contourlets, steerable wavelet filters,
short-time-Fourier transforms, or designed by adapt-
ing its content to fit a given set of signal example
(Aharon, 2006) (Mairal, 2009). The former is simple
and fast, and the selection of function should base on
how suitable they are to sparsely describe the signals
in question; the latter usually is more suitable for the
given set of signals, but it is more expensive in com-
putational cost.
Gabor wavelets were introduced to EEG signal
analysis due to their biological relevance and com-
putational properties. Gabor functions (Mallat, 1993)
NCTA 2011 - International Conference on Neural Computation Theory and Applications
16

in wavelets provide optimal joint time-frequency
localization.
Gabor dictionary D
g
is constructed as follows:
D
g
=g
r
(
t
)
,r ∈ Γ, (2)
where,
g
γ
(
t
)
=K(γ)e
-π

t-u
s

2
cos(2πω(t-μ)+φ)
(3)
where, g
r
(
t
)
is the Gabor atom. K(γ) is normaliza-
tion factor to ensure g
r
(t)=1 . Each element in
parameter set γ=

μ,s,ω,φ

represents separately the
position, scale, frequency and phase of Gabor atom.
A series of Gabor atoms which can be created by
different parameters of

μ,s,ω,φ

compose an over-
complete dictionary D
g
=g
r
(
t
)
, r∈Γ.
2.3 Matching Pursuit
Given an overcomplete dictionary D=g
1
,g
2
,⋯,g
n

(n is the number of atoms in dictionary D), the rep-
resentation of a signal have many or infinite possible
combinations. Sparse representation based on over-
complete dictionary is to find the best matched and
the sparsest combination.
The following objective function (Mallat, 1993)
is minimized:
J(α)= f
(
t
)
-
∑
α
i
g
γ
i
(
t
)
M
i=1

2
2
+λ
‖
α
‖
0
.
(4)
where, f is the original signal,




⋯
represents
the indices of the chosen atoms g


and α
i
is decom-
posing coefficient corresponding to
g


.
‖
α
‖

is the
ℒ

norm, and it is the number of nonzero compo-
nents in the vector α. Minimizing the former item of
the formula can find the best matched approximate,
and minimizing the latter item can find the sparsest
one. The parameter λ>0 is a scalar regularization
parameter that balances the tradeoff between recon-
struction error and sparisity. Due to its nature of
combinational optimization, it is a NP hard problem
to find the solution to equation (4). Suboptimal solu-
tions to this problem can be obtained by iterative
methods such as the matching pursuit (MP) (
Mallat,
1993) (Mallat, 1994). MP is a greedy algorithm that
optimizes the signal approximation by iteratively
selecting atoms which best match the signal struc-
tures at each step.
In the first step of MP, the atom g


that best
matches the signal f is chosen. In each of the con-
secutive steps, the atom g


is matched to the resid-
ual signal R

f.
The procedure of MP can be described by Equa-
tion (5).



R

f=f
R

f=
〈
R

f,g


〉
g


+
R

f
g


=argmax



∈

〈
R

f,g


〉

(5)
2.4 Bayesian Decision Rule
In Pattern Recognition, there are a variety of deci-
sion rules, but only Bayesian Decision Theory is
optimal (
Christopher, 2006). Bays Decision Theory is
based on the popular Bays theorem, which is essen-
tially an expression of conditional probabilities.
Conditional probabilities represent the probability of
an event occurring given evidence.
p
(


|
x
)
=
(|

)(

)
()
=
(|

)(

)
∑
(|

)(

)


(6)
Where, i=1,⋯,k, k is the number of classes. If
p
(
ω

)
=pω

,i≠j, then equation (6) was simpli-
fied as:
p
(


|
x
)
=
(|

)
∑
(|

)


.
(7)
The classification rule becomes:
x∈

,
(8)
where,


=max
(


|

)
=
(|

)
∑
(|

)


.
(9)
3 EEG SIGNAL
CLASSIFICATION BASED ON
SPARSE REPRESENTATION
3.1 Algorithm Framework
In this study, EEG signals of normal and epileptic
patients are used. Epileptic seizure detection in EEG
can be thought as a classification problem. It in-
cludes data acquisition, feature extraction, and clas-
sification procedure. According to the property of
EEG, a novel EEG signal classification method is
proposed, which based on sparse representation of
signal and Bays classifier. The procedure of the
proposed method can be summarized as follows:
Step 1: Divide every EEG signal sample into some
sub-samples. Since in the process of sparse represen-
tation, the dimension of signal is equivalent to the
dimension of the atoms of dictionary, sub-samples
can greatly save the storage space and avoid tre-
EPILEPTIC ELECTROENCEPHALOGRAM SIGNAL CLASSIFICATION BASED ON SPARSE REPRESENTATION
17

mendous computation.
Step 2: Construct the overcomplete dictionary.
Figure 1: Flow chart of the system.
Step 3: Find the better atoms in the given diction-
ary and their decomposed coefficients for every sub-
sample by MP, and select decomposed coefficients
and atom parameters as features to formulate the
training set and test set for classification.
Step 4: Train the Bayesian classifier by training set.
Step 5: Test the performance of Bayesian classifier
by test set.
Fig.1. show the flow chart of the method.
In the Framework, the algorithm of feature ex-
traction is our main contribution which will be de-
scribed in the following section.
3.2 Feature Extraction based on Sparse
Representation
Motivated by the compressive sensing theory that
since sparse representation can recover signal with-
out any significant information loss, can it be used
as signal feature for classification? In (Huang, 2007)
the coefficients of sparse representation based on the
same atoms which are optimized based on all sam-
ples in average are used as features for classification.
So the selected atoms for sparse representation must
not be the best for single sample. In this paper, a
new features for classification based on sparse repre-
sentation are proposed. Different from feature ex-
traction method in (Huang, 2007), better atoms and
coefficients in sparse representation of each sample
are taken as features for classification in this study.
Every EEG signals epoch x can be represented
as:
x=
∑







.
(10)
Where, N is the number of atoms in Gabor Diction-
ary. The coefficients of sparse representation of one
of EEG epochs are shown as Figure 2, from which it
can be seen that the signal is sparse. The bigger
coefficients are, the more main signal information
their corresponding atoms should contain. So, the
bigger coefficients and their corresponding atoms
parameters are taken as features.
The features for classification are denoted as:
 =

α

,μ

,s

,ω

,φ


,i=1⋯
(11)
Where M is the number of selected dictionary atoms
for classification. Then, the number of features used
for classification will be 5*M. The selection of M
and N which are critical for classification perform-
ance will be studied in next section.
Figure 2: The coefficients of sparse representation.
4 EXPERIMENT
4.1 Data
The public available data described in (Andrzejak,
2001) is used. The complete data set consists of five
sets (denoted as Z, O, N, F and S) and each contains
100 single-channel EEG segments. The dimension
of the raw data set is 4096. Sets Z and O consist of
segments taken from surface EEG recordings that
were carried out on five healthy volunteers using a
standardized electrode placement scheme. Volun-
teers were relaxed in an awake state with eyes open
(Z) and eyes closed (O), respectively. Sets N, F and
S originated from EEG archive of presurgical diag-
nosis. Segments in set F were recorded from the
epileptogenic zone, and those in set N from the hip-
pocampal formation of the opposite hemisphere of
the brain. While set N and F contained only activity
measured during seizure free intervals, set S only
contained seizure activity. Here, segments are se-
Begin
Dividing every sample
into sub-sam
p
les
Feature extraction (find the sparse representations
of each sub-saples with MP, and find better atoms
and coefficients as features
Sample features in each class were
randoml
y
divided as train set and test set
Training Bayesian
classifier
Classify with
Ba
y
esian classifier
NCTA 2011 - International Conference on Neural Computation Theory and Applications
18

lected from all recording sites exhibiting ictal activ-
ity.
The data were digitized at 173.61 samples per
second using 12 bit resolution. Band-pass filter set-
tings were 0.53 – 40 Hz (12dB/oct). Because the
dataset Z included the signals from normal people
and S contained signal from epileptic patient’s sei-
zure activity. In this paper, two dataset (Z and S) of
the complete dataset are used.
4.2 Experiential Results
In this study, the test performance of the classifiers
can be evaluated by the computation of sensitivity,
specificity and total classification accuracy. The
sensitivity, specificity and total classification accu-
racy are defined as follows:
Sensitivity (A true positive decision): number of
positive decisions by computer /number of actually
positive cases.
Specificity (A true negative decision): number of
negative decisions by computer /number of actually
negative cases.
Total classification accuracy: number of correct
decisions by computer /total number of cases.
A true negative decision occurs when both the
classifier and the physician suggest the absence of a
positive detection. A true positive decision occurs
when the positive detection of the classifier
coincides with a positive detection of the physician.
Accuracy, sensitivity and specify are used as a
performance measure.
4.2.1 The Performance of Proposed
Algorithm
For the dimension of the raw data set is very high,
every sample is divided into 17 sub-samples firstly.
So the dimension d of 4096 is reduced to 241. Gar-
ber dictionary, which is constructed by equation (2)
and (3), are used in sparse representation. The para-
meters of atoms are chosen from dyadic sequences
of integers. Their sampling is governed by extra
integer parameters: j (0≤≤log

, N is signal
size), p (0≤≤×2
()
), k (0≤≤2
()
)
and i (0≤≤12). Parameters of Gabor atoms are
discretized by the following ways: γ=

μ,s,ω,φ

=

2

,1 2
⁄
ps,(πk) s,π 6
⁄⁄
. Every subsample is
represented by sparse representation based on MP,
and feature vector is formed according to equation
(11). Here the number of atoms in Gabor Dictionary
N and the number of features for classification
which is in direct proportion to the number of se-
lected dictionary atoms for classification M are criti-
cal for classification performance. The number of
features for classification is 5×M. The relationship
between classification accuracy and the number of
features and the size of dictionary will be discussed
in 4.2.3. Here, N is set 14638, and M is set 1, so the
number of features for classification is 5; 90% sam-
ple features are randomly drawn from each class as
training sample to train the Bays classifier. The
remaining samples are used as test sample. The
number of the training samples and test samples are
summarized in Table1. All experiments are repeated
1000 times, and the final results are the averaged of
them. The classification results are showed in Ta-
ble2. From it, we can see that the average classifica-
tion accuracies, sensitivity and specificity could
reach 100%, when the size is 14638 and the number
of features is 5.
Table 1: The number of the training samples and test
samples.
Class Training set Testing set Total
Epileptic 1530 170 1700
Normal 1530 170 1700
Total 3060 340 3400
Table 2: The classification results with proposed methods.
Classification Accuracy /
standard variance
Sensitivity Specificity
100%/0 100% 100%
There are many other methods proposed for the
epileptic EEG signal classification. Table 3 presents
a comparison on the results between the method
developed in this work and other methods. Only
methods evaluated in the same dataset are included.
The classification accuracies are listed in the table
for comparison. From Table 3, it can be seen that the
accuracy obtained from our method is the best
among the comparison methods.
4.2.2 The Performance of Proposed
Algorithm on Noisy Data
In our experience, these EEG segments were se-
lected and cut out from continuous multichannel
EEG recordings after visual inspection for artefacts,
e.g., due to muscle activity or eye movements. To
test the robustness of this method to noise, random
white Gaussian noise with increasing level of energy
are added to each original signal. The experiences
are conducted with the same parameters, pre-
processing and algorithms as with the previous sub-
section. The classification results are showed in
Table 4, and decreasing curves of classification
accuracies are showed in figure 3.
EPILEPTIC ELECTROENCEPHALOGRAM SIGNAL CLASSIFICATION BASED ON SPARSE REPRESENTATION
19

Table 3: The classification accuracy and the number of
features of our method and other methods.
Researchers Method Accuracy
Number
of input
features
Srinivasan et al.
Time & Frequency
domain features-recurrent
neural network
99.6% 5
Polat et al. FFT-decision tree 98.72% 129
Nigam and
Graupe
Nonlinear pre-processing
filter-NN
97.2% 2
Subasi
DWT-mixture of expert
model
95% 16
Tzallas
Time frequency analysis-
ANN
99% 13
Ling
Guo(Guo2011)
GP-based feature
extraction-KNN classifier
GP-based feature
extraction-KNN classifier
99.2% 2.32
This work
Sparse representation of
signal—Bays classifier
100% 5
Table 4: The classification results with different levels of
white Gaussian noise.
Noise
Intensity
Classification Accuracy/
Standard Deviation
Sensitivity Specificity
Noiseless 100%/0 100% 100%
10% 99.99%/ 0.0027 100% 99.97%
20% 99.73%/ 0.0149 99.46% 100%
30% 99.41%/ 0.0223 98.83% 100%
40% 98.46%/0.0288 96.91% 94.6%
Figure 3: Classification accuracies decreasing curve.
We can see from them, the classification accura-
cies slightly decline with the increase of noise level.
When data is polluted with 10% Gaussian noise, the
classification accuracy still could reach 99.99%
which decease only 0.01%; the standard deviation is
only 0.0027. Ever if when the intensity of noise
reaches 40%, the performance of classifier are still
relatively stable.
4.2.3 The Relationship between
Classification Accuracy and the
Number of Features, the Size of
Dictionary
In order to studies the relationship between classifi-
cation accuracy and the number of features, the size
of dictionary separately. In experiences, M is set
separately from 1 to 10, and N is set separately
as115804, 32305, 14638, 5889, 3861, 1495, 1001,
806, 715 and 520 which are obtained by different
step-length of parameters: j, p, k and i. The classifi-
cation accuracies are showed in Table 5. Form it, we
can see that there are classification accuracies of
100% in every line. This demonstrates that when the
size of dictionary is fixed, average classification
accuracies could reach 100%, only that the number
of features is properly set.
Figure 4 show the relationship between classifi-
cation accuracy and the number of feature (5×M)
given dictionary size. From it, we can see: (a) when
dictionary sizes are 32305 and 14638, the classifica-
tion accuracies maintain steadily at 100% ,no matter
how many the atoms are selected for classification;
(b) when the size of dictionary are 1495, 1001, 806,
715, and 520, the classification accuracies grow with
the number of features increasing, and all reach
100% when M are separately equal or greater than 3,
2, 6, 6 and 7; (c) when the size of dictionary are
115804, 5889 and 3861, the classification accu-
racies grow with the number of features increasing,
and all reach 100% when M are separately 3,4 and 5;
but with the numbers of atoms selected for classifi-
cation M continue to rise, the right rates decreases.
Figure 5 show the relation between classification
accuracy and the size of dictionary given feature
number. From it, we can see: (1) when the size of
dictionary are equal or greater than 1495, all of the
classification accuracy are higher than 99%
whatever how many atoms are selected for
classification; (2) when the size of dictionary are
less than 1495, the accuracies are not stable, and is
sensitive to the number of features.
4.3 Discussion
From those experience with noiseless and noise data,
we see that when the noise is increased, the accuracy
degrades slightly. This indicates that classification
features which are constructed by coefficients and
atom parameters of sparse representation are robust
to noise, thus yield less performance degradation.
The results of Epilepsy Seizure Detection based
on sparse representation and Bayesian classifier are
NCTA 2011 - International Conference on Neural Computation Theory and Applications
20

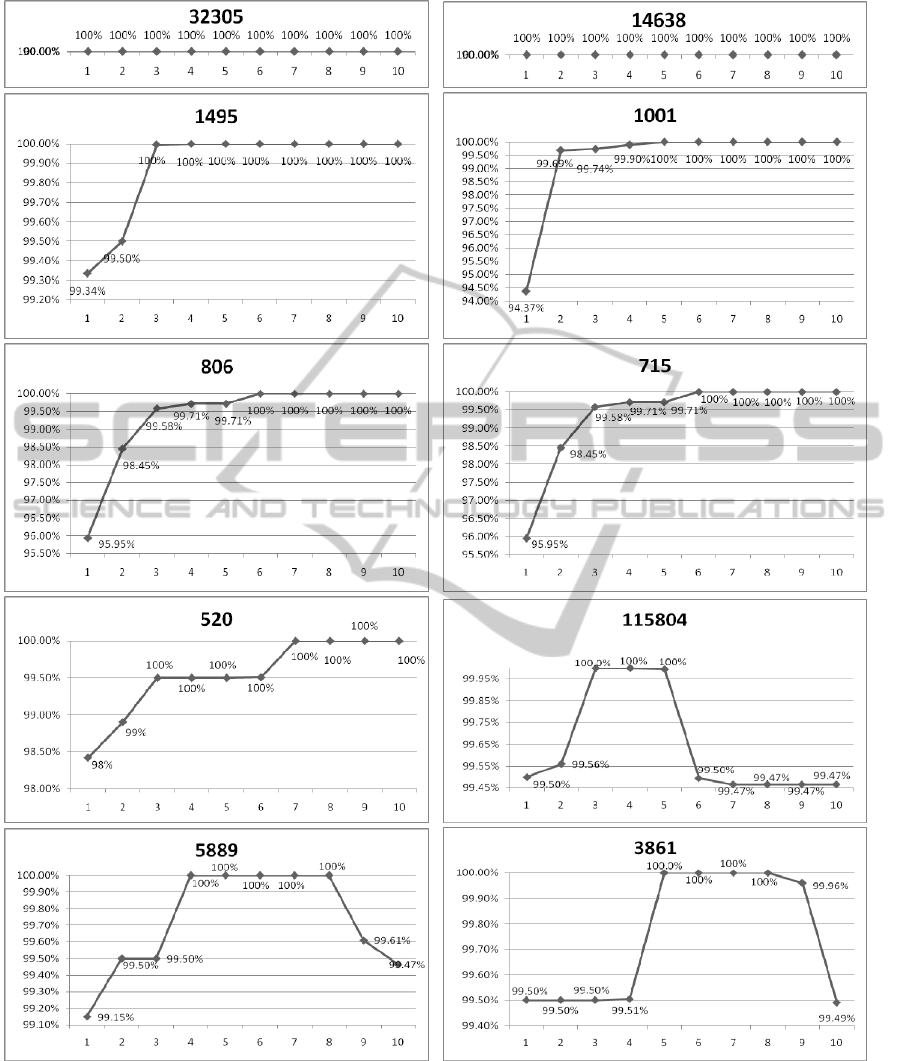
Figure 4: Classification accuracies with different number of atoms selected for classification given dictionary size.
perfect, and are robust to noise only that the proper
parameters are set. This is consistent with the theory
that sparse representations can capture the inherent
structure of signal.
In feature selection based on sparse representa-
tion, the size of dictionary N and the number of
atoms selected for classification M are critical. Form
the results of section 4.2.3, we see the classification
accuracies raise with the number of atoms selected
for classification increases, most of them could
reach accuracies of 100% when M is properly set;
however, with M continue to raise, some of classifi-
EPILEPTIC ELECTROENCEPHALOGRAM SIGNAL CLASSIFICATION BASED ON SPARSE REPRESENTATION
21

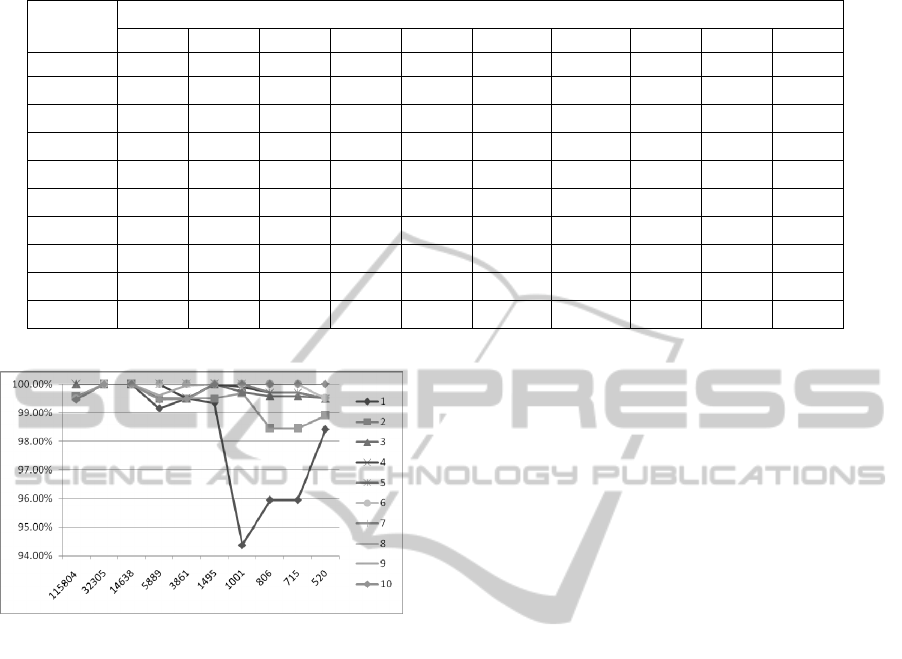
Table 5: classification right rate based on different number of features and different sizes of dictionary.
Dictionary
sizes N
Atom numbers selected for sparse representation M(feature Number=5*M)
1 2 3 4 5 6 7 8 9 10
115804 99.50% 99.56% 100% 100% 100% 99.50% 99.47% 99.47% 99.47% 99.47%
32305 100% 100% 100% 100% 100% 100.00% 100.00% 100% 100% 100%
14638 100% 100% 100% 100% 100% 100.00% 100.00% 100% 100% 100%
5889 99.15% 99.50% 99.50% 100% 100% 100.00% 100.00% 100% 99.61% 99.47%
3861 99.50% 99.50% 99.50% 99.51% 100% 100.00% 100.00% 100% 99.96% 99.49%
1495 99.34% 99.50% 100% 100% 100% 100.00% 100.00% 100% 100% 100%
1001 94.37% 99.69% 99.74% 99.90% 100% 100.00% 100.00% 100% 100% 100%
806 95.95% 98.45% 99.58% 99.71% 99.71% 100.00% 100.00% 100% 100% 100%
715 95.95% 98.45% 99.58% 99.71% 99.71% 100.00% 100.00% 100% 100% 100%
520 98.42% 98.91% 99.50% 99.50% 99.50% 99.51% 100.00% 100% 100% 100%
Figure 5: classification accuracies with different size of
dictionary given number of features.
cation accuracies decrease. One of the possible rea-
sons for this is that when M is small, the number of
features for classification is also small, so the classi-
fication accuracies is lower; when M is big enough,
the accuracies reach 100%;but when M is too larger,
the noise is included into features for classification
and result in degrading of the classification accura-
cies.
Form the results of section 4.2.3, we also can see
that when the size of dictionary is large enough, the
classifications accuracies are relatively stable, and
are less affected by the number of features. However,
the larger the size of dictionary is, the longer the
time to finding the better atoms for classification in
dictionary with MP is; when the size of dictionary is
small, the classification accuracies are not stable, in
order to obtain higher classification accuracy, the
number of features must be increased. Similarly, the
bigger the number of features is, the longer the time
to finding the better atoms for classification in dic-
tionary and training and testing classifier. So the
select of M and N is very critical not only to classifi-
cation accuracies but also the efficiency of algorithm.
Only if the number of features is properly set, the
classification accuracies could be perfect.
Compare with other methods, the classification
accuracies is best as illustrated in Table 3. The aver-
age accuracy of our method even for noisy data is
higher than that of most other methods in Table 3 for
non-noise data.
5 CONCLUSIONS
Diagnosing epilepsy is a difficult task requiring
observation from the patient, EEG, and gathering
additional clinical information. Different etiologies
of seizures result in different treatments. In this
paper, a new classifier based on sparse representa-
tion and Bays classifier is proposed for epileptic
seizure detection in EEG. Since sparse representa-
tion can capture the inherent structures of signal, the
proposed features are relative robust to some noise.
In sparse representation, the size of dictionary is
very critical to classification accuracies and the
efficiency of algorithm. When the size of dictionary
is bigger, the classification accuracies are relatively
stable and perfect, but the time to finding the better
atoms will be long. In the selection of features for
classification, the number of features is also critical
to classification accuracies and efficiencies of algo-
rithm. The classification accuracies raise with the
number of features increases, most of them could
reach 100% of accuracies when the number of fea-
tures is properly set; however, with the number of
features continue to raise, some of classification
accuracies decrease due to that the atoms represent-
ing the noise is included into features for classifica-
tion. Comparison with the other methods, the accu-
racy of the proposed method is relatively high. The
NCTA 2011 - International Conference on Neural Computation Theory and Applications
22

classification of normal subjects and epileptic pa-
tients were done with the accuracy of 100%, only if
when the number of features for classification M and
the size of dictionary N are properly set.
Although the proposed method has shown good
performance on the EEG signal classification, there
still remain some problems to be solved. The speed
is relatively slow and the selection of dictionary size
and number of features is a key point to classifica-
tion accuracy. So how to speed up the sparse repre-
sentation calculation and how to automatically de-
termine the size of dictionary and the number of
features suitable to EEG classification are our future
work.
ACKNOWLEDGEMENTS
The authors wish to thank the anonymous reviewers
for their useful suggestions and comments on the
paper. And the authors also would like to express
their sincere thanks to Ms. Xiuling Zhou for her
many useful suggestions.
The research work described in this paper was
fully supported by the grants from the National
Natural Science Foundation of China, (Project No.
90820010, 60911130513) Prof. Guo is the author to
whom the correspondence should be addressed, his
E-Mail address is [e-mail]
REFERENCES
Nigam, V., & Graupe, D., 2004. A neural-network-based
detection of epilepsy. In Neurological Research,
26(1), 55–60.
Srinivasan, V., Eswaran, C., & Sriraam, N., 2005. Artifi-
cial neural network basedepileptic detection using
time-domain and frequency-domain features. In Jour-
nal of Medical Systems.
Güler, N., Übeyli, E. & Güler, I., 2005. Recurrent neural
networks employing Lyapunov exponents for EEG
signals classification. In Expert Systems with Applica-
tions, Subasi, A. ,2005-A. Automatic recognition of
alertness level from EEG byusing neural network and
wavelet coefficients. In Expert Systems with Applica-
tions, Subasi, A.,2005-B. Epileptic seizure detection
using dynamic wavelet network. In Expert Systems
with Applications.
Subasi, A., 2006.Automatic detection of epileptic seizure
using dynamic fuzzy neural networks. In Expert Sys-
tems with Applications.
Subasi, A., 2007. Application of adaptive neuro-fuzzy
inference system for epileptic seizure detection using
wavelet feature extraction, In Computers in Biology
and Medicine.
Subasi, A., 2007. EEG signal classification using wavelet
feature extraction and a mixture of expert model, In
Expert Systems with Applications 32 (4) (2007)1084–
1093.
Übeyli, E., 2009. Combined neural network model em-
ploying wavelet coefficientsfor EEG signals classifica-
tion. In Digital Signal Processing.
Ocak, H., 2009. Automatic detection of epileptic seizures
in EEG using discretewavelet transform and approxi-
mate entropy. In Expert Systems with Applications.
Wright, J., Yang, A. Y., Ganesh, A., Sastry, S. S. and Ma,
Y., 2009.Robust Face Recognition via Sparse Repre-
sentation, In IEEE Transactions on Pattern Analysis
and Machine Intelligence(PAMI).
Huang, K., and Aviyente, S., 2007. “Sparse representation
for signal classification,” In NIPS.
Richard, G., Baraniuk. Compressive Sensing., 2007. In
IEEE Signal Processing Magazine [118] July.
Zhang, Ch., Yin, Zh., Chen, X. D., and Xiao, M. X., 2005.
Signal overcomplete representation and sparse decom-
position based on redundant dictionaries, In Chinese
Science Bulletin.
Aharon, M. Elad, M. Bruckstein, A.M., 2006. The K-
SVD: an algorithm for designing Overcomplete Dic-
tionaries for Sparse Representation, In signal Process-
ing, IEEE.
Mairal, J. Bach, F. Ponce, J. and Sapiro, G., 2009. Online
dictionary learning for sparse coding, In ICML.
Mallat, S. and Zhang, Z., 1993. Matching pursuits with
time-frequency dictionaries, In IEEE Transactions on
Signal Processing.
Mallat, S. Davis, G. and Zhang, Z., 1994. Adaptive time-
frequency decompositions, In SPIE Journal of Optical
ngineering.
Donoho, D. and Huo, X., 2001. Uncertainty principles and
ideal atomic decomposition, In
IEEE Trans.on Infor-
mation Theory .
Guo, L., et al., 2011. Automatic feature extraction using
genetic programming: An application to epileptic EEG
classification. In Expert Systems with Applications
(2011).
Andrzejak, R., Lehnertz, K., Mormann, F., Rieke, C.,
David, P., & Elger, C., 2001. Indications of nonlinear
deterministic and finite-dimensional structures in
timeseries of brain electrical activity: Dependence on
recording region and brainstate.IN Physical Review E.
Christopher M. Bishop, 2006 Pattern Recognition and
Machine Learning, Springer Science+Business Media,
Turkey.
EPILEPTIC ELECTROENCEPHALOGRAM SIGNAL CLASSIFICATION BASED ON SPARSE REPRESENTATION
23