
AN IMPROVED METHOD TO SELECT CANDIDATES ON METRIC
INDEX VP-TREE
Masami Shishibori
1
, Samuel Sangkon Lee
2
and Kenji Kita
1
1
Institute of Technology and Science, The University of Tokushima, Tokushima, Japan
2
Dept. of Computer Science and Engineering, Jeonju University, Jeonju, Republic of Korea
Keywords:
Multimedia retrieval systems, Indexing technique, Vantage point tree, Triangule inequality.
Abstract:
On multimedia databases, it is one of important techniques to use the efficient indexing method for the fast
access. Metric indexing methods can apply for various distance measures other than the Euclidean distance.
Then, metric indexing methods have higher flexibility than multi-dimensional indexing methods. We focus on
the Vantage Point tree (VP-tree) which is one of the metric indexing methods. VP-tree is an efficient metric
space indexing method, however the number of distance calculations at leaf nodes tends to increase. In this
paper, we propose an efficient algorithm to reduce the number of distance calculations at leaf nodes of the VP-
tree. The conventional VP-tree uses the triangle inequality at the leaf node in order to reduce the number of
distance calculations. At this point, the vantage point of the VP-tree is used as a reference point of the triangle
inequality. The proposed algorithm uses the nearest neighbor (NN) point for the query instead of the vantage
point as the reference point. By using this method, the selection range by the triangle inequality becomes
small, and the number of distance calculations at leaf nodes can be cut down. Moreover, it is impossible to
specify the NN point in advance. Then, this method regards the nearest point to the query in the result buffer
as the temporary NN point. If the nearer point is found on the retrieval process, the temporary NN point is
replaced with new one. From evaluation experiments using 10,000 image data, it was found that our proposed
method could cut 5%∼12% of search time of the conventional VP-tree.
1 INTRODUCTION
In recent years, as a result of the lower price and larger
capacity of main memory and secondary storage de-
vices, it has become possible for personal comput-
ers to store large amounts of multimedia data such
as text, images, music, and videos. Consequently,
there is a growing need for technologies that permit
fast and accurate retrieval of the desired data from a
large amount of stored multimedia data. To improve
the search efficiency, it is necessary to first extract the
desired features of the target data and to create an in-
dex based on these features. During the search pro-
cess, the appropriate data can be obtained by access-
ing only the index. The indexing technology has a
large influence on the retrieval efficiency.
The features extracted from multimedia data are in
general expressed as vectors, and the retrieval process
is executed based on the distances among feature vec-
tors. The methods used to transform feature vectors
into indices, i.e., the methods for indexing multidi-
mensional data, include the R-tree (Guttman, 1984),
R*-tree (Beckmann et al., 1990), SS-tree (White and
Jain, 1996), SR-tree (Katayama and Satoh, 1997), X-
tree (Berchtold et al., 1996), VA-FILE (Weber et al.,
1998), and others. However, these methods take for
granted the use of the Euclidean distance as a dis-
tance measure and they cannot cope with other mea-
sures. Examples of non-Euclidean distance measures
include the quadratic-form distance (Ioka, 1989) that
considers correlations among the dimensions of mul-
tidimensional data, the Edit distance that expresses
the similarity among strings of characters, and the
earth mover’s distance (Rubner et al., 1999).
In order to solve this issue, research on metric-
space indexing has been conducted. The construc-
tion of multidimensional indices is based on the carte-
sian values of the features in multidimensional space.
In contrast, the only requirement of the metric-space
index is the metric space postulates (Zezula et al.,
2006), and therefore it is possible to create such an
index using only information on the distances among
feature vectors. As a consequence, distance measures
other than the Euclidean distance can be used. The
314
Shishibori M., Sangkon Lee S. and Kita K..
AN IMPROVED METHOD TO SELECT CANDIDATES ON METRIC INDEX VP-TREE.
DOI: 10.5220/0003668803060311
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 306-311
ISBN: 978-989-8425-79-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

metric-space index is in general represented as a hi-
erarchical tree structure. The search space is got nar-
row during the search process by a recursive splitting
of the space (data set) based on the distance infor-
mation. Several schemes such as the M-tree (Ciac-
cia et al., 1995), VP-tree (Yianilos, 1993)(Fu et al.,
2000), MVP-tree (Bozkaya and Ozsoyoglu, 1997),
and MI-tree (Ishikawa et al., 1999) have been pro-
posed based on different space-splitting methods. In
the M-tree, the index tree is formed by a bottom-
up process during the space splitting. The disadvan-
tage of this method is that it introduces many com-
mon regions in the spaces resulting from the split,
which implies a lower search efficiency. The VP-
tree uses a pivot point called the vantage point and
splits the space in a top-down manner based on a hy-
persphere. The splitting does not introduce common
regions. During the search process, the nodes in the
search range are traversed starting from the root node.
Eventually, leaf objects linked to leaf nodes are ac-
cessed and their distances are calculated. These dis-
tances are used to decide whether or not the associ-
ated objects are located in the search range. However,
the calculation of the distances of the leaf nodes tra-
versed by the search process tends to increase the total
number of distance calculations, resulting in a lower
search speed. To solve this problem, in the VP-tree
a triangle inequality is applied to the leaf objects to
reduce the number of distance calculations.
In this paper, we propose an algorithm to reduce
the number of distance calculations at leaf nodes of
the VP-tree. In the conventional VP-tree, the van-
tage point is used as a reference point for the triangle
inequality. In the proposed method we note that the
selection range tends to get narrower as the distance
between the reference point of the triangle inequality
and the query object gets smaller, and thus we reduce
the number of distance calculations using the nearest
neighbor (NN) object (with respect to the query ob-
ject) as the reference point for the triangle inequality.
How to specify the NN object as the reference
point? It is impossible to identify in advance the NN
object. Thus, The nearest object to the query in the
result buffer is regarded as the temporary NN object.
If the nearer object is found on the retrieval process,
the temporary NN object is replaced with new one.
Furthermore, in order to use the triangle inequality
with the temporary NN object as the reference point,
we must know all the distances between the tempo-
rary NN object and all the objects related to the leaf
nodes of these objects. Since the temporary NN ob-
ject cannot be determined in advance, in practice we
need all the distances among the objects. During the
construction of the indexing we construct a distance-
list file by computing the distances among objects. It
is worth noting, however, that the file size is reduced
by splitting this large file into a file for each object.
After explaining the VP-tree construction and
search algorithm in Section 2, we will describe the
selection method for leaf nodes. Section 3 introduces
an improvement to the leaf-node selection algorithm.
Section 4 describes experiments with and an evalua-
tion of the improvement method. Finally, Section 5
provides a summary and points to future issues.
2 VP-TREE
2.1 Construction Algorithm
We now explain the VP-tree construction algorithm.
Suppose that we want to perform indexing of a data
set S containing N data points. At each node of the
tree, the vantage point (hereafter referred to as vp) is
selected using a random algorithm as described be-
low.
1. Select a temporary random vp from the data set.
2. Calculate the distance from the provisional vp to
the other N − 1 objects.
3. Calculate the mean and variance of these dis-
tances.
4. Repeat steps 1 through 3 several times and select
as the vp the point that leads to the largest vari-
ance.
Let µ be the mean of the distances from the root
node (selected as the vp) to all data points in S. If
d(p, q) is the distance between points p and q, then
the data set s is split into S1 and S2 as shown below:
S
1
= {s ∈ S | d(s, vp) < µ}
S
2
= {s ∈ S | d(s, vp) ≥ µ}
Continue by recursively applying this splitting oper-
ation to S1 and S2. All the subsets such as S1 and
S2 correspond to nodes in the VP-tree. Moreover, the
leaf nodes contain a number of objects.
2.2 Search Algorithm
We use the range search and k-nearest neighbor search
algorithms in the VP-tree. Range search involves
specifying the query object and the search radius (the
range) and retrieving the set of objects located at a
distance up to the specified radius from the center of
the circle. K-nearest neighbor search involves des-
ignating the query object and the number of search
hits k, so that the k objects with the smallest distances
AN IMPROVED METHOD TO SELECT CANDIDATES ON METRIC INDEX VP-TREE
315
are obtained in order, starting from the closest one.
The experiments of the present paper are based on k-
nearest neighbor search. However, since the k-nearest
neighbor search algorithm is based on range search,
both methods are explained here.
In the range search method, the nodes within the
search range are traversed starting from the root node.
The distances between the leaf objects linked to leaf
nodes and the query object are calculated, and the ob-
jects located inside the search range are found. On the
other hand, in the k-nearest neighbor search method,
the initial value of the search radius is set to infin-
ity, and the objects that are traversed are appended
to the search-result list, starting from the root. If the
number of retrievals in the search-result list exceeds
a specified limit, the retrieved object with the maxi-
mum distance is removed, so that the number of items
in the list does not exceed the specified value. Here,
the maximum distance in the search-result list is taken
to be the search radius. The search radius is reduced
by repeating this process, resulting eventually in the
specified number of search results.
2.3 Method to Select Candidates on
Leaf-nodes
In the conventional VP-tree, result candidates in the
search range are selected by applying the triangle in-
equality to the objects corresponding to leaf nodes tra-
versed during the search (Yianilos, 1993). We now
describe this process. For each leaf node, the dis-
tances between the node’s vp object and each leaf ob-
ject are stored as a distance list when the VP-tree is
constructed (at the registration phase). By applying
the triangle inequality to the distances between the vp
object and each leaf object, we can reduce the num-
ber of distance calculations. The following theorem
holds, where q is a query object, r is the search range,
v is a vp object of a leaf node, and o is an object linked
to a leaf node. Moreover, v is called by the reference
point of the triangle inequality.
Theorem 1.
If |d(v, o) − d(v, q)| > r, then leaf object o is not
in the search range.
Proof.
From the triangle inequality d(v, q) + d(q, o) ≥
d(v, o) ,
d(v, o) − d(v, q) > r implies that d(q, o) > r,
and therefore object o is not in the search range.
Similarly, −d(v, o) + d(v, q) > r
and thus d(q, o) > r.
Therefore, Theorem 1 is proved.
q
r
v
o
Figure 1: Selection of candidates using a vantage point as
the reference point of the triangle inequality.
Input : q , r , L
Output : L
SearchLeaf (q , r , L)
{
foreach o (all objects in the leaf node) {
if ( |d(v , o) ¡ d(v , q)| ¡ r ) {
if ( d(o , q) ¡ r ) {
add o to L, set r to the max distance;
}
}
}
}
q : query object
r : radius of search range
o : object in the leaf node
v : vp object
L : search result
Figure 2: Search algorithm on the leaf node for k-nearest
neighbor search.
As for Theorem 1, r is given by the user and d(v, o)
can be obtained from the distance list which is con-
structed at the registration phase. Moreover, d(v, q)
can be computed only once for each leaf node dur-
ing the search process. Therefore, the objects outside
the search range can be specified without calculating
d(q, o) by using the triangle inequality of Theorem
1, and the number of distance calculations can be re-
duced. The result candidate selection for leaf nodes
is shown in Fig.1. The k-nearest neighbor search al-
gorithm is illustrated in Fig.2. The non-shaded part
of Fig.1 corresponds to the portion where the inequal-
ity of Theorem 1 holds. The distance calculation can
be skipped for objects located in this area. The shaded
area correspondsto the portion where Theorem 1 does
not hold. The distance calculation is necessary for ob-
jects located in this area.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
316

3 SELECTION METHOD USING
NEAREST NEIGHBOR
OBJECTS
If vp is used as the reference point in the triangle in-
equality explained in the previous section, the effect
of the selection tends to increase as the portion where
Theorem 1 does not hold (shaded area of Fig.1) gets
smaller. The external radius of this portion corre-
sponds to the distance from vp to the query object q
added to the search range radius r. Since r is fixed
for a given search query, the selection becomes more
effective as the distance between vp and q decreases.
On the other hand, the object closest to q is the near-
est neighbor object. By using the object nearest to
q instead of vp as the reference point in the triangle
inequality, it is possible to reduce the area where The-
orem 1 does not hold. Therefore, we propose a candi-
date selection method that uses the triangle inequality
with the nearest neighbor object as a reference point.
The following theorem holds, where q is the query
object, r is the search range radius, o
nn
is the neigh-
bor object in the search list closest to the query object,
and o is an object linked to a leaf node.
Theorem 2.
If d(o
nn
, o) − d(o
nn
, q) > r, then leaf object o is
not in the search range.
Proof.
From the triangle inequality d(o
nn
, q) + d(q, o) ≥
d(o
nn
, o) ,
d(o
nn
, o) − d(o
nn
, q) > r implies that d(q, o) > r,
and therefore object o is not in the search range.
Therefore, Theorem 2 is proved.
Thus, if d(o
nn
, o) and d(o
nn
, q) are known, it is
possible to know whether or not an object is in the
search range without calculating the distance to each
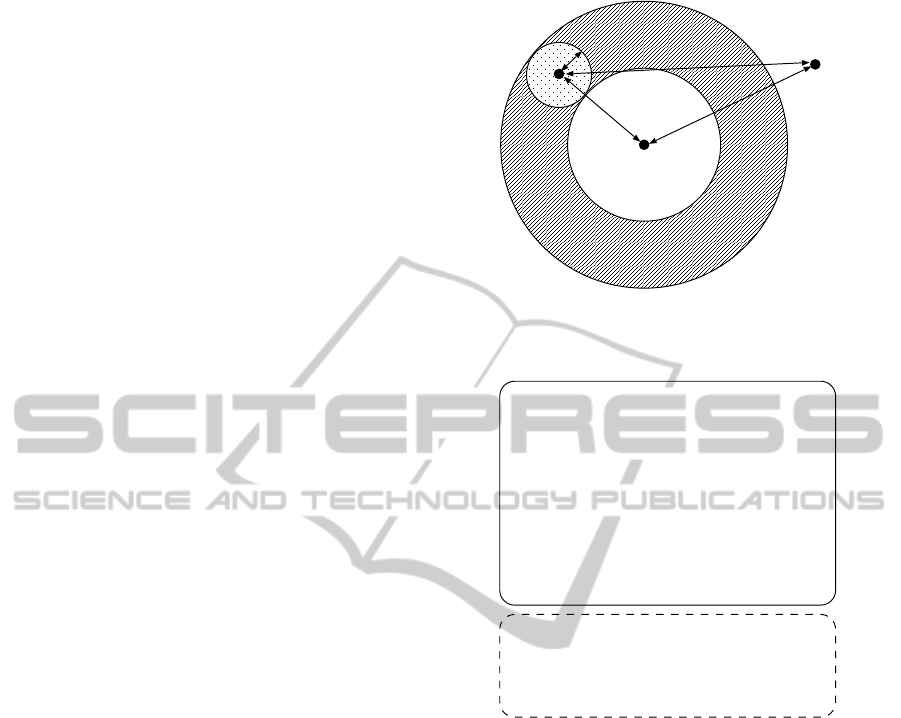
leaf object. This situation is illustrated in Fig.3. In
other words, if no leaf object exists in the shaded part
of Fig.3, it is possible to skip the computation of the
distance to the query object. The actual leaf-node
search algorithm is illustrated in Fig.4. It is usually
not possible to identify in advance the nearest neigh-
bor objects. Thus, the nearest neighbor object o
nn
is
provisionally assumed to be the object in the search
result list L that has the shortest distance from the
query object q, as shown in Fig.4. The provisional
nearest neighbor object o
nn
is renewed every time a
new object is found in the search range during the
search process. Theorem 2 also applies to the dis-
tance between the provisional nearest neighbor object
and the query object.
Moreover, the value of d(o
nn
, o) in Theorem 2 is
known if a list exists containing distances between
q
r
o
nn
o
Figure 3: Selection of candidates using a nearest neighbor
point as the reference point of the triangle inequality.
Input : q , r , L
Output : L
SearchLeaf (q , r , L)
{
foreach o (all objects in the leaf node) {
if ( d(o
1
, q) + r ¡ª d(o
1
, o) ) {
if ( d(o , q) ¡ r ) {
add o to L, set r to the max distance;
}
}
}
}
q : query object
r : radius of the search range
o : object in the leaf node
o
1
: nearest neighbor object in the search result
L : search result
Figure 4: Search algorithm on the leaf node by the proposed
method.
the nearest neighbor object and the objects in the leaf
nodes. However, since it is not possible to know in
advance which object will become the nearest neigh-
bor of q, in practice all the objects must be considered
as candidates for o
nn
. Therefore, for the indexing it
is necessary to compute the distances from each leaf
object to all the other objects and so create a distance-
list file. Since it is difficult to hold such a large file
in memory, we adopt the file structure of the distance-
list is shown in Fig.5. In the proposed method, as
shown in Fig. 5, the distance-list file is split into a file
for each object and each file is managed separately in
the secondary memory. Thus, only the distance list
related to the provisional nearest neighbor object is
read into the memory. For example, suppose the pro-
visional nearest neighbor object is o
2
. In this case,
only the distance list related to o
2
in the second line
of Fig. 5 is read. Moreover, the distance list is read
only when the provisional nearest neighbor object is
renewed. By forming the distance-list file according
AN IMPROVED METHOD TO SELECT CANDIDATES ON METRIC INDEX VP-TREE
317

d(O
1, O1), d(O1, O2), L , d(O1, On )
O1
!
!
!
!
!
!
Secondary Memory
d(O
2, O1), d(O2, O2), L , d(O2, On)
O 2
d(O
n, O1), d(On, O2), L , d(On, On)
On
Distance List of O1
Distance List of O2
Distance List of On
Onn
Figure 5: Content of the distance list file.
to this scheme, we can reduce the size of the file and
the number of read accesses.
In the implementation, an ID was assigned to each
object, a distance list was created by considering each
object ID as a file name, and a distance-list file con-
sisting of a group of files was constructed. How-
ever, to avoid OS-related restrictions on the maximum
number of files in a directory, the lowest digits of the
IDs were divided into triples. The three lowest dig-
its formed the file name and the next three formed the
directory. In other words, we restricted the maximum
number of files per directory to 1,000.
4 EVALUATION
4.1 Experimental Method
The proposed method was implemented in a VP-tree
and an experiment with a similar-image search task
was carried out. The computer used ran the Linux OS
and was equipped with a 3.2 GHz PentiumD CPU and
2G of memory. 10,000 photographic images (Corel,
2011) were used as registered images and features
were extracted from HSI histograms of the image fea-
ture vectors. The k-nearest neighbor search was per-
formed on 1,000 input images that had not been used
for the indexing in order to calculate the time, num-
ber of distance calculations, and average CPU time
required for one image search. The quadratic-form
distance was used as the distance measure.
An similar algorithm using nearest neighbor
objects is AESA(Approximating and Eliminating
Search Algorithm) (Vidal, 1986). The AESA uses a
distance-list file that is previously created and con-
tains the computed distances among objects, without
constructing an index tree such as the VP-tree. Since
the proposed method is based on an algorithm similar
to AESA, we use AESA as a benchmark to evaluate
the VP-tree candidate reduction improvement using
nearest neighbor objects.
200
400
600
800
1000
1200
1400
1600
1800
2000
2200
10 20 30 40 50 60 70 80 90 100
calc_num
k
vp_all
vp_nn
vp_all_nn
AESA
Figure 6: Number of distance calculations on 96 dimen-
sional data.
0.01
0.015
0.02
0.025
0.03
0.035
0.04
10 20 30 40 50 60 70 80 90 100
cpu-time[sec]
k
vp_all
vp_nn
vp_all_nn
Figure 7: CPU-time on 96 dimensional data.
4.2 Experimental Results
Using the improved method, we conducted an exper-
iment on k-nearest neighbor search. The legends in
the graph correspond to the methods below.
• vp all: reduction method using multiple vp.
• vp nn: reduction method using nearest neighbor
objects.
• vp all nn: reduction method using a combination
of vp all and vp nn.
• AESA: reduction method based on AESA.
Experimental results for the number of distance
calculations for 96 dimensions are shown in Fig.6.
Fig.7 shows experimental results for the cpu time
for 96 dimensions. Fig.8 shows experimental results
for the cpu time using AESA for dimensions rang-
ing from 12 to 96. The horizontal axis k represents
the number of retrievals while the vertical axis “calc
num” shows the number of distance calculations.
The figures show that the number of distance
calculations decreases in the order vp all, vp nn,
vp all nn. Note that there is no significant difference
between vp all and vp nn, but a 10% improvement
is obtained in the case of vp all nn. A possible ex-
planation is that candidate reduction based on nearest
neighbor objects takes place in a different range than
that for the usual vp, and the range reduces more ef-
fectively if the methods are used in parallel.
In terms of execution time, the improvement for
100 retrievals and 48 dimensions is about 5%. For
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
318

0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
10 20 30 40 50 60 70 80 90 100
cpu-time[sec]
k
dim12
dim24
dim48
dim96
Figure 8: CPU-time of AESA on each dimensional data.
100 retrievals and 96 dimensions, the improvement
increases to about 12%. Thus, an effective gain is ob-
tained with the present method even when the num-
ber of dimensions increases. The maximum number
of splits per leaf node was set to 10. The size of the
file that stores the distance list that is needed in the
candidate reduction method based on nearest neigh-
bor objects was 313 MB for all dimensions.
Fig.8 indicates that although AESA outperforms
the VP-tree in terms of the number of distance cal-
culations, the retrieval time is slower. A possible
reason for this is the difference in the number of
read accesses to the distance-list file. For AESA, the
distance-list file must be read at every iteration of the
process. In other words, this file is read as many
times as the number of distance calculations, and this
is thought to have a large influence on the retrieval
time. For the VP-tree, the distance-list file needs to be
read only for the reduction of leaf objects, and there-
fore the number of read accesses can be reduced to a
minimal level. Thus, the VP-tree resulted in a more
significant improvement in the retrieval effectiveness
than did AESA.
5 CONCLUSIONS
We have proposed an improvement to the search al-
gorithm for the leaf nodes of a VP-tree. The results
show that the retrieval times were reduced by 5% to
12% for the task involving retrieval of similar images.
A topic for future work is the creation of a search al-
gorithm that permits further reductions in the distance
calculations with a smaller index size.
ACKNOWLEDGEMENTS
This work was supported in part by a grant from
the Grant-in-Aid for Scientific Research numbered
#21500940, #21300036 and #20650143 from the
Ministry of Education, Science and Culture, Japan.
REFERENCES
Beckmann, N., Kriegel, H. P., Schneider, R., and Seeger,
B. (1990). The r*-tree: An efficient and robust access
method for points and rectangles. In Proc. of the ACM
SIGMOD ’90, pages 322–331.
Berchtold, S., Keim, D. A., and Kriegel, H. P. (1996). The
x-tree an index structure for high-dimensional data. In
Proc. of the 22nd VLDB, pages 28–39.
Bozkaya, T. and Ozsoyoglu, M. (1997). Distance-based in-
dexing for high-dimensional metric spaces. In Proc.
of the ACM SIGMOD, pages 357–368.
Ciaccia, P., Patella, M., and Zezula, P. (1995). M-tree: An
efficient access method for similarity search in metric
spaces. In Proc. of the ACM SIGMOD Int. Conf. on
the Management of Data, pages 71–79.
Corel (2011). Corel image garally. http://www.corel.co.jp/.
Fu, A. W., Chan, P. M., Cheung, Y. L., and Moon, Y. S.
(2000). Dynamic vp-tree indexing for n-nearest neigh-
bor search given pair-wise distances. VLDB Journal,
pages 2–8.
Guttman, A. (1984). A dynamic index structure for spatial
searching. In Proc. of the ACM SIGMOD ’84, pages
47–57.
Ioka, M. (1989). A method of defining the similarity of
images on the basis of color information. Technical
Report RT-0030.
Ishikawa, M., Notoya, J., Chen, H., and Ohbo, N. (1999).
A metric index mi-tree. Transactions of Information
Processing Society of Japan, 40(SIG6(TOD3)):104–
114.
Katayama, N. and Satoh, S. (1997). Sr-tree : An in-
dex structure for nearest neighbor searching of high-
dimensional point data. IEICE Transaction on Infor-
mation and Systems, J80-D-I(8):703–717.
Rubner, Y., Tomasi, C., and Guibas, L. J. (1999). The
earch mover’s distance, multi-dimensional scaling,
and color-based image retrieval. In Proc. of the ARPA
Image Understanding Workshop, pages 661–668.
Vidal, R. (1986). An algorithm for finding nearest neigh-
bours in approximately constant average time. Pattern
Recognition Letters, pages 145–157.
Weber, R., Schek, H. J., and Blott, S. (1998). A quantitative
analysis and performance study for similarity-search
methods in high-dimensional spaces. In Proc. of the
24th VLDB, pages 194–205.
White, D. A. and Jain, R. (1996). Similarity indexing with
ss-tree. In Proc. of the 12th Int. Conf. on Data Engi-
neering, pages 516–523.
Yianilos, P. N. (1993). Data structures and algorithms for
nearest neighbor search in general metric spaces. In
Proc. of the ACM-SIAM SODA’93, pages 311–321.
Zezula, P., Amato, G., Dohnal, V., and Batko, M. (2006).
Similarity Search –The Metric Space Approach –.
Springer press.
AN IMPROVED METHOD TO SELECT CANDIDATES ON METRIC INDEX VP-TREE
319
